Введение
Одной из насущных задач в преподавании вообще и в преподавании математики в частности является перевод образовательных программ на современные рельсы. При этом возникают весьма сложные проблемы, трудно поддающиеся решению. Дело в том, что если рассматривать цикл обучения в целом от начальной и до высшей школы, то начинать всегда приходится с нуля, а путь к современному знанию становится всё длиннее.
Это обстоятельство заставляет либо сохранять архаические во многих отношениях курсы, либо жертвовать развитием навыков, которые традиционно считались совершенно необходимыми. При этом, как показывает опыт, не удаётся добиться согласия по вопросу о том, что архаично, а что до сих пор актуально. Причина такого разнобоя во мнениях достаточно ясна. Спорящие стороны различным образом понимают цели образования. При этом одни хотят воспитать профессионального математика, другие - инженера, третьи - умного и образованного человека, четвёртые - идеального потребителя.
Авторы статьи полагают, что наиболее важным является воспитание умного и образованного человека. Как показывал в своих полемических статьях И.В. Арнольд, «крутая» модернизация нанесла ущерб, в том числе и сообществу профессионалов. Появились, в частности, математики, которые не умеют считать. При этом речь идёт не о сложных расчётах, а тех навыках, которые были доступны недавно едва ли не каждому школьнику младших классов.
Авторы данной статьи полагают, что одним из разумных путей модернизации математического образования является пропедевтика важных разделов высшей математики. При этом следует не просто выбрать тему и дать учащимся связанный с ней, но достаточно случайный набор заданий. Необходима кропотливая предварительная работа, направленная на отбор базовых понятий, задач и интуитивно воспринимаемых учащимися образов, о чём авторы писали в статье «Роль образного мышления в научном мышлении».
В данной же статье рассматривается пропедевтика решения экстремальных задач. Как известно, подобные задачи играют важную роль в различных областях науки и техники. К ним зачастую сводятся многие проблемы, возникающие в экономике, промышленности и сельском хозяйстве. Как правило, решение этих задач требует применения достаточно сложного математического аппарата, изучаемого в высших учебных заведениях. Однако многие задачи на максимум и минимум могут быть решены элементарными средствами без использования высшей математики. Решение таких задач весьма полезно для учащихся в качестве пропедевтики соответствующей тематики.
При изучении соответствующих вопросов авторы опираются на понятия, связанные с восприятием пространства, и интуитивно близкие учащимся. Речь идёт о следующем наборе понятий:
-
Расстояние на плоскости.
-
Расстояние на искривлённой поверхности.
-
Геодезическая линия.
-
Линия уровня.
-
Градиент.
-
Экстремум.
-
Геометрическое преобразование, понимаемое, как формализация понятия движения.
Расстояние на плоскости
Перейдём к изложению конкретных вопросов.
Задача 1. Рассмотрим для начала задачу о нахождении минимального пути из точки
А в точку В с заходом на прямую l.
Более точная формулировка этой задачи выглядит следующим образом. Даны точки А и В, расположенные по одну сторону от прямой l (рис.1). Точка С лежит на прямой l. Требуется определить, при каком положении точки С на прямой l, сумма расстояний АС + СВ будет минимальной.
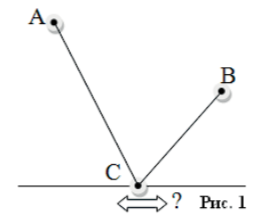
Эта задача имеет также многочисленные формулировки практического содержания. Приведём одну из них.
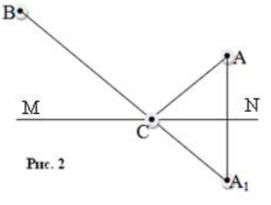
Два посёлка А и В лежат на одном берегу реки l. Где надо построить водокачку С так чтобы общая длина АС + СВ водопроводов в эти посёлки была минимальной?
Среди различных решений этой задачи самым простым является геометрическое. Пусть А1 - точка, симметричная точке А относительно прямой 1, С - точка пересечения прямых А1 и l (рис. 2).
Покажем, что точка С является искомой. Действительно, пусть С1 - произвольная точка прямой l, отличная от точки С. Тогда, используя свойства симметрии относительно прямой l и применяя неравенство треугольника к треугольнику А1С1В, получим:
АС1+ С1В = А1С1+ С1В > А1В = А1С + СВ = АС + СВ
или
АС1 + С1В > АС + СВ,
то есть для любой точки С’ прямой l, отличной от точки С, указанная сумма расстояний больше, чем сумма расстояний для точки С.
Оказывается, что кроме геометрического решения задачи есть и физическое её истолкование. Речь идёт о законах оптики, один из которых утверждает, что угол падения равен углу отражения. Это правило связано с тем, что свет идёт от точки к точке по кратчайшему пути. Итак, тот факт, что углы ВСМ и ACN равны, легко доказать геометрически и обосновать с помощью законов оптики, которые полезно применять при решении экстремальных задач.
Далее мы покажем, как простые факты, только что полученные нами можно применять для решения более сложных задач. Но для этого нам понадобится понятие линии уровня. Сначала определим линию уровня для некоторой величины. Множества точек, в которых некоторая величина, например, расстояние, принимает постоянное значение, называется линиями уровня этой величины.
Концентрические окружности как пример линий уровня
Одна из важнейших геометрических фигур, - окружность, представляет собой множество точек равноудалённых от центра этой окружности. Таким образом, если мы рассмотрим точку О на плоскости и семейство концентрических окружностей с центром О, то каждая из окружностей семейства является линией уровня для расстояния от точки О.
Переход от окружности к окружности большего радиуса можно трактовать как рост одной и той же окружности, то есть можно рассматривать фигуры семейства как ка фазы движения, например, как круг на глади воды.
Отвлекаясь на минуту от чисто математической тематики, но сохраняя связь с проблемами воспитания человека, отметим, что даже созерцание таких прекрасных линий как прямая и окружность является необходимым моментом полноценного развития. Тем более желательно, чтобы учащийся, развивая свою мелкую моторику, научился строить эти линии с помощью классических инструментов - линейки и циркуля. Естественно, это пожелание вызовет крайнее раздражение у приверженцев «чистой» математики, служащей только себе самой.
В этой связи процитируем известного французского математика Жана Дьедонне [Дьедонне, 1972]: «... нужно научить ребёнка искусству геометрических построений, но при этом следует как чумы избегать этого воплощённого анекдота классического обучения - ограничения допустимого набора инструментов лишь циркулем и линейкой». Вопрос о том, чем строить, учёный муж оставляет открытым. Главное - не циркулем и линейкой.
Конечно, в процессе исторического изменения образования что-то безвозвратно теряется. Так авторы статьи с завистью смотрят на каллиграфические этюды А.С. Пушкина и Ф.М. Достоевского. А вот на то, как пишут современные молодые люди, воспитанные под эгидой неограниченной свободы, приходится взирать с содроганием. Хочется, чтобы хотя бы циркуль всё же сохранился.
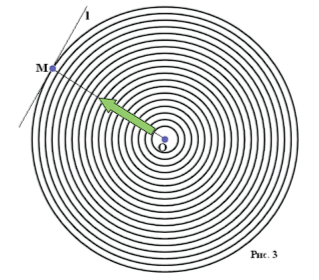
Пусть прямая l не проходит через точку О. Тогда она удалена от этой точки на некоторое расстояние r. Это означает, что концентрические окружности нашего семейства, разрастаясь, сначала не будут пересекаться с прямой l. Но при достижении радиуса r соответствующая окружность соприкоснётся с этой прямой. Соприкосновение произойдёт в ближайшей к окружности точке М, лежащей на прямой l. При этом отрезок ОМ будет перпендикулярен прямой l (рис. 3).
Определение градиента
Описанная нами простая динамическая модель должна послужить прообразом моделей более сложных. Если снова рассмотреть её с позиций геометрической оптики, то окружности, рассматриваемые до этого, как линии уровня, предстанут волновыми фронтами, а их радиусы - лучами, движущимися по кратчайшим расстояниям. По этой причине именно в направлении радиусов наиболее стремительно нарастает расстояние от центра, а, значит, радиусы являются линиями градиента, то есть направлениями наибольшего возрастания соответствующей величины. Линии градиента в каждой точке перпендикулярны линиям уровня.
Перейдём к более сложным процессам. При их описании мы будем говорить о линиях уровня не отдельных величин, а функций, зависящих сразу от нескольких величин. Множества точек, в которых функции двух переменных принимают постоянные значения, называются линиями уровня этих функций.
Рассмотрим линии уровня функции суммы расстояний АМ + МВ, где А и В - две различные фиксированные точки.
Эллипсы
Эллипсом называется множество точек М, таких что для двух различных фиксированных точек А и В выполняется условие АМ + МВ = const. Точки А и В называются фокусами эллипса.
Оговоримся, что Если АМ + МВ < с и с < AB, то множество точек М пусто. Если АМ + +МВ = с = АВ, то множество точек М совпадает с отрезком АВ. Если же АМ + МВ = с > АВ, то множество точек М представляет собой полноценный невырожденный эллипс с фокусами А и В. Будем в дальнейшем эллипс, соответствующий сумме расстояний, равной с, обозначать через Ес.
Возможно простое и наглядное построение эллипса с помощью нити и двух гвоздиков (рис. 4). Возможно, к такой смене инструментов и призывал Дьедонне.

Софокусные эллипсы как линии уровня
Если два эллипса имеют одинаковые фокусы, то они называются софокусными. Дадим описание семейства софокусных эллипсов, как «раздувающегося» семейства, схожего с семейством концентрических окружностей.
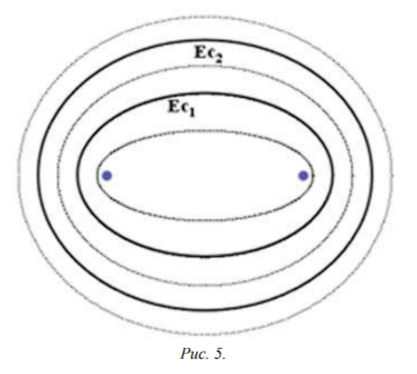
Изобразим на плоскости семейство софокусных эллипсов Ес, где АМ + МВ = с, А и В - фокусы и с > АВ (рис. 5). Очевидно, что если с1 < с2 , то эллипс Ес1 лежит внутри эллипса Ес2. Поэтому для внутренних точек М эллипса Ес выполняется неравенство АМ + МВ < с, для граничных точек М эллипса Ес справедливо равенство АМ + МВ = с, для внешних точек М эллипса Ес имеет место неравенство АМ + МВ > с.
Оптическое свойство эллипса
Если l - некоторая прямая, не пересекающая отрезок АВ, то найдётся эллипс Ес, принадлежащий указанному семейству, касающийся прямой l в некоторой точке С. Тогда все точки С’ прямой l, отличные от С, лежат вне эллипса Ес и, следовательно, АС + С’ В> > АС + СВ, т.е. точка С даёт решение задачи, поставленной в начале этой статьи, и поэтому Zack = ZACL. Таким образом, фокальные радиусы АС и ВС эллипса Ес образуют равные углы с касательной l (рис. 6). Поскольку, как мы уже говорили, при отражении света от прямой l падающий и отражённый лучи образуют равные углы с этой прямой, то доказанное свойство называется оптическим свойством эллипса. Если считать эллипс зеркальным и поместить источник света в фокусе а, то отражённые лучи соберутся в фокусе В (рис. 7).
Точка Торричелли
Похожим способом можно решить следующую задачу.
Найти в плоскости треугольника АВС точку М такую, что сумма расстояний МА + МВ + МС от этой точки до вершин треугольника АВС наименьшая.
Построим семейство софокусных эллипсов с фокусами А и С и семейство концентрических окружностей с центром в точке В (рис. 8). Ясно, что в точке минимума суммы расстояний МА + МВ + МС один из эллипсов первого семейства должен касаться некоторой окружности второго семейства, так как в случае пересечения эллипса и окружности, проходящих через точку М, для всех точек Р, принадлежащих пересечению внутренней области эллипса и круга, сумма РА + РВ + РС будет меньше суммы МА + МВ + МС. Обозначим точку касания эллипса и окружности через Т, а их общую касательную - через KL. Тогда ∠ATK = ∠CTL и ∠ATB = ∠ATB = ∠ATK + ∠KTB = ∠CTL + ∠LTB = ∠CTB, поскольку ∠KTB = ∠LTB = 900 в силу перпендикулярности радиуса ВТ окружности касательной KL. Итак, ∠ATB = ∠CTB.
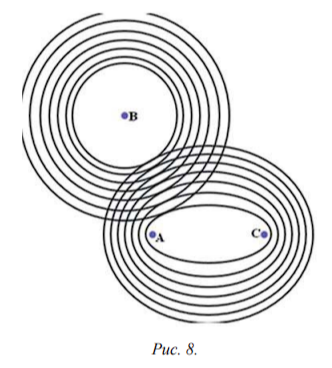
Проведя аналогичные рассуждения для семейства софокусных эллипсов с фокусами A и В и семейства концентрических окружностей с центром в точке С, получим, что ∠ATC = ∠CTB. Таким образом, ∠ATC = ∠CTB = ∠ATB = 1200.
Точка Т называется точкой Торричелли треугольника АВС. Для ее построения достаточно построить на сторонах АВ, ВС, СА треугольника АВС правильные треугольники АВС1, ВСА1, САВ1 внешним образом, т. е. так, чтобы точки А и А1, В и В1, С и С1 лежали по разные стороны от прямых ВС, СА, АВ и описать около треугольников окружности, которые пересекутся в точке T (рис. 9).
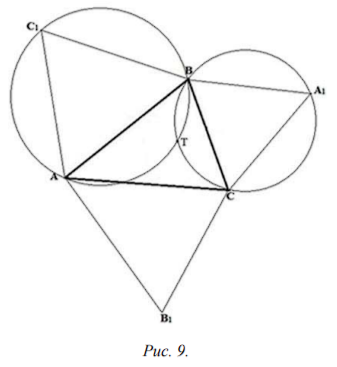
Действительно, пусть Т - точка пересечения описанных окружностей треугольников
АВС1 и ВСА1. Тогда
∠ATB =1800 - ∠AC1B = 1800 - 600 = 1200 = 1800 - ∠BA1C = ∠CTB
и
∠ATC = 3600 - ∠ATB - ∠CTB = 3600 - 1200 - 1200 = 1200,
т.е. описанная окружность треугольника САВ1 также проходит через точку Торричелли Т. Итак, решение получено с помощью достаточно простых и ясных рассуждений.
Что касается вопроса о направлении линий градиента в случае, когда в качестве линий уровня рассматриваются софокусные эллипсы, то ими являются софокусные (с теми же фокусами) гиперболы. Элементарное доказательство этого факта дано в [Куланин, 2001].
На данный момент мы можем подвести предварительный итог, состоящий в том, что, отправляясь от расстояния на плоскости можно рассмотреть ряд экстремальных задач, решение которых не только элементарно, но и опирается на интуитивно прозрачные пространственные образы. Перечислим решённые нами задачи.
-
Поиск минимального пути с заходом на прямую.
-
Рассмотрение семейств концентрических окружностей и софокусных эллипсов как линий уровня.
-
Получение метода построения касательных к эллипсу.
-
Вывод оптического свойства эллипса.
-
Построение точки Торричелли.
Дальнейшее продвижение пропедевтики экстремальных задач можно связать с важным понятием геодезической линии. Рассмотрим какую-либо искривлённую поверхность. Движение по ней из точки А в точку В можно осуществить многими способами, но один из путей является кратчайшим. Именно эта кратчайшая линия на поверхности называется геодезической.
Изучение геодезических линий в общем случае проводится сложными методами дифференциальной геометрии. Однако существует два вида поверхностей, геодезические на которых могут быть описаны наглядными и элементарными методами.
Начнём с линейчатых развёртывающихся поверхностей. Такие поверхности являются частным случаем линейчатых поверхностей, которые образованы непрерывным движением прямой. При этом их можно без растяжений и сжатий развернуть и наложить на плоскость. При этом все геодезические перейдут в прямые [Кривошапко, 2006].
Примерами развёртывающихся поверхностей являются конусы и цилиндры. Эти поверхности не только наглядно представимы, но и легко моделируются с помощью листа бумаги. Все рассмотренные выше задачи переносятся на развёртывающиеся поверхности.
Учащемуся, например, может быть предоставлено следующее задание, которое на первый взгляд имеет экспериментальный характер. Он получает свёрнутый из бумаги конус-кулёк с двумя помеченными точками. Нужно начертить на конусе геодезическую линию, соединяющую эти точки. Правильное решение таково. Нужно разрезать конус по образующей, развернуть на плоскость стола, провести прямую, через заданные точки и склеить конус заново.
Вторым типом поверхностей, позволяющим успешно работать с геодезическими, являются сферы. Как известно, геодезическими линиями на сфере являются линии большого круга [Прасолов, 2004]. При этом вычисления расстояний на сфере не составляет труда, поскольку его можно измерять угловой мерой кратчайшей дуги большого круга, соединяющей эти точки. Кроме того, вся образная система, применяемая нами на плоскости, переносится на сферу, в частности это относится к задаче о нахождении минимального пути на сфере из точки А в точку В с заходом на геодезическую.
Более того, на любой поверхности могут быть введены аналоги кривых второго порядка, называемые геодезическими эллипсами и гиперболами [Фиников, 2010]. При этом, как и на плоскости, геодезические эллипсы и гиперболы образуют ортогональную сеть. В полной мере это относится и к сфере. При указанном нами способе определения расстояний можно определить на сфере аналоги кривых второго порядка. Например, эллипс - множество точек, сумма расстояний от каждой из которых до двух фиксированных точек, называемых фокусами, постоянна.
Чтобы подчеркнуть особую специфику возникающей при этом сферической геометрии, отметим, что любая линия большого круга на сфере одновременно является прямой (геодезической), окружностью, равноудалённой от каждого из двух полюсов, и сферическим эллипсом.
Очень интересен и тот факт, что любая сферическая гипербола с фокусами F1 и F2 одновременно является сферическим эллипсом с фокусами Р1 и F2, где Р1 является точкой, диаметрально противоположной фокусу F1. Точно также и любая сферическая парабола одновременно является сферическим эллипсом. Доказательство этих фактов совершенно элементарно.
Для нас же особенно важно то, что при наличии таких отличий геометрии сферы от геометрии плоскости метод, предназначенный для построения касательных к эллипсам на сфере, без существенных изменений переносится и сюда. Он позволяет строить касательные к сферическим эллипсам как биссектрисы углов между фокальными радиусами. Таким образом, перед учащимся возникает круг экстремальных задач, связанных с новой геометрией, но решаемых схожими методами.
Теперь и на сфере мы рассматриваем геодезические эллипсы как линии уровня. Что же касается линий градиента, то их нахождение связано со следующей теоремой: если на сфере заданы две точки F1 и F2, а точка F3 является диаметрально противоположной к точке F1, то любой сферический эллипс с фокусами F1 и F2 ортогонален любому сферическому эллипсу с фокусами F2 и F3 (рис. 10).
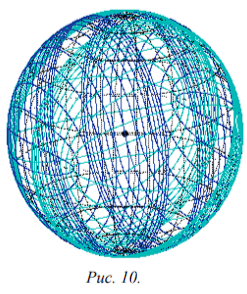
Итак, нами очерчен достаточно представительный круг экстремальных задач, решаемых простыми и наглядными методами.
Две геометрические задачи на экстремум
В заключение рассмотрим ещё две геометрические задачи на экстремум. Для этого сначала напомним, что треугольник А1В1С1 называется вписанным в треугольник АВС, если его вершины лежат на сторонах треугольника АВС. Для определенности можно считать, точки А1, В1, С1 лежат соответственно на сторонах ВС, СА, АВ треугольника АВС (рис. 11).
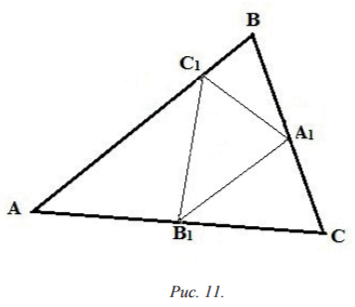
Задача 1. Среди всех треугольников, вписанных в данный остроугольный треугольник АВС, найти треугольник минимального периметра.
Задача 2. Среди всех правильных треугольников, вписанных в данный треугольник АВС, найти треугольник минимального периметра.
Несмотря на похожие формулировки, эти задачи значительно отличаются по степени известности. Если первая задача имеет давнюю историю и достаточно широко известна, то вторая задача известна гораздо меньше. По имеющимся у авторов сведениям, впервые она была поставлена российским геометром Д.П. Мавло в 1981г. [Mavlo, 1981], а её решение, принадлежащее тому же автору, было опубликовано в канадском математическом журнале Crux mathematicorum в 1982г. [Mavlo, 1982]. Мы приведём решение задачи 2, использующее аналогию с решением задачи 1, отличное от авторского Д.П. Мавло [Mavlo, 1982].
Отметим также, что частный случай данной задачи для египетского треугольника был недавно рассмотрен Б.Н.Кукушкиным [Кукушкин, 2017].
Покажем сначала, что решением задачи 1 является ортоцентрический треугольник HaHbHc остроугольного треугольника АВС, вершины которого совпадают с основаниями высот треугольника АВС.
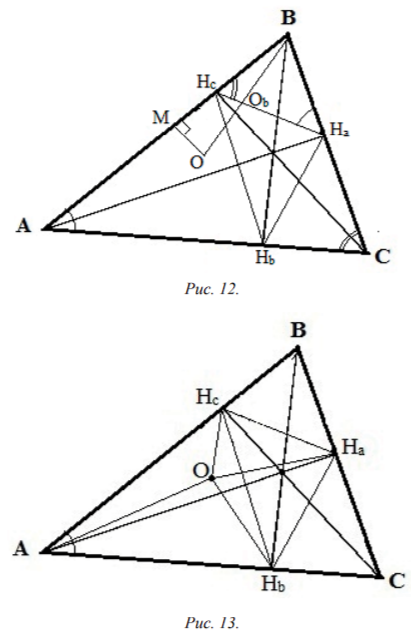
Хорошо известно, что треугольники AHbHc, BHcHa, CHaHb подобны треугольнику АВС (см, например, задачу 4.2 [Куланин, 2016]). Пусть точка О - центр описанной окружности треугольника АВС (рис. 12), М - середина АВ.
Тогда ∠MOB=1/2∠AOB=∠ACB, поскольку вписанный угол АСВ равен половине центрального угла АОВ, поэтому из прямоугольного треугольника ОМВ получаем ∠MBO = 900 - ∠MOB = 900 - ∠ACB = ∠HbBC, т.е. радиус описанной окружности и высота, выходящие из одной вершины треугольника, образуют равные углы со сторонами треугольника, выходящими из той же вершины (на рис. 2 изображен остроугольный треугольник, общий случай рассмотрен в задаче 4.12 [Куланин, 2016]). Далее, ∠BHcHa = ∠ACB в силу подобия треугольников HBH, и АВС, откуда вытекает, что ∠BHcHa + ∠OBHc = ∠ACB + ∠HbBC = 900, т.е. ∠HcObB = 900, где Ob - точка пересечения прямых ОВ и HcHa. Таким образом, радиус ОВ описанной окружности треугольника АВС перпендикулярен стороне HaHc ортоцентрического треугольника HaHbHc. Аналогично, ОА ∠ HbHc и ОС ∠ HHb.
Теперь легко выразить площадь треугольника АВС через радиус его описанной окружности R и периметр PH его ортоцентрического треугольника HaHbHc. Соединим центр О описанной окружности с основаниями высот Ha, Hb, Hc треугольника АВС (рис. 13).
Тогда площадь треугольника АВС равна сумме площадей четырехугольников AHbOHc, BHcOHa, CHOHb, диагонали которых взаимно перпендикулярны:
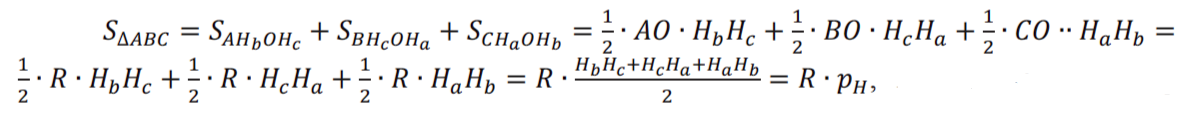
полупериметр ортоцентрического треугольника HHbH В результате получили формулу , весьма похожую на известную формулу , где r - радиус вписанной окружности треугольника АВС.
Теперь мы имеем все факты, необходимые для решения задачи 1. Соединив центр О описанной окружности треугольника АВС с вершинами А В С1 вписанного треугольника А1В1С1 и обозначив углы между диагоналями четырехугольников АВ1ОС1, ВС1ОА1, СА1ОВ1 через а, ß, у соответственно (рис. 14), получим:
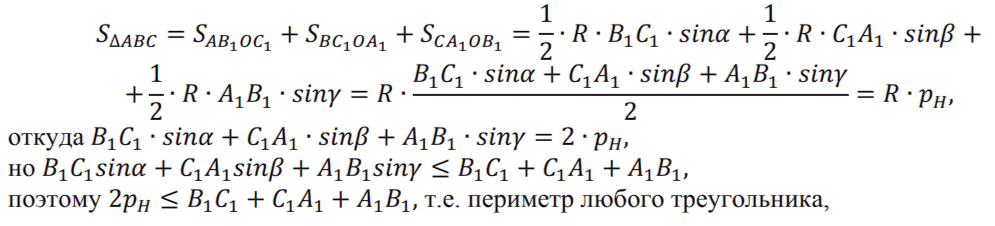
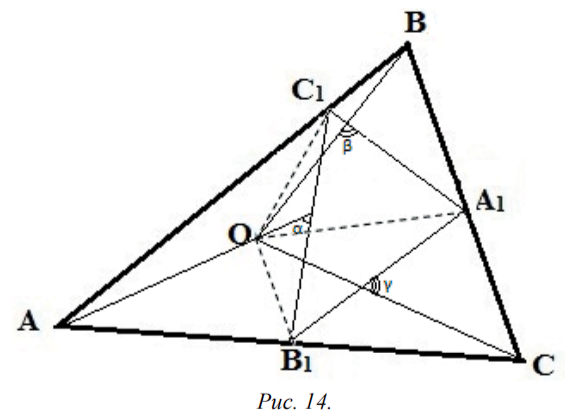
вписанного в остроугольный треугольник АВС, не меньше периметра ортоцентрического, откуда и следует, что ортоцентрический треугольник имеет минимальный периметр среди всех вписанных треугольников.
Для решения задачи 2 нам понадобится понятие изогональности.
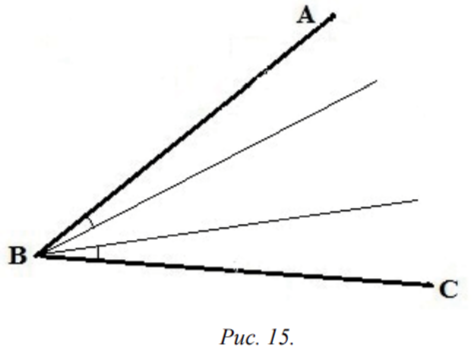
Определение 1. Две прямые, проходящие через вершину угла и образующие равные углы с биссектрисой этого угла, называются прямыми, изогональными относительно этого угла.
Очевидно, что прямые, изогональные относительно данного угла, образуют равные углы со сторонами этого угла (рис. 15).
Предложение 1. Пусть прямые, проведенные через вершины треугольника АВС, пересекаются в одной точке Р, не лежащей на его описанной окружности. Тогда изогональные им прямые также пересекаются в одной точке . При этом точки Р и называются изогонально сопряженными или просто изогональными относительно треугольника АВС (например, как это фактически доказано выше, центр описанной окружности и ортоцентр изогональны).
Доказательство.
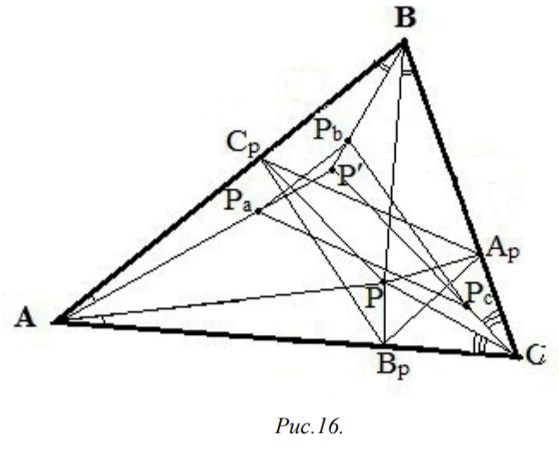
Обозначим основания перпендикуляров, опущенных из точки Р на прямые ВС, СА, АВ через А Bp, Cp соответственно (рис. 16), а ортоцентры треугольников ABpCp, BCpAp, CApBp - соответственно через Pa Pb Pc. Тогда в четырехугольнике BApPCp углы РАрВ и РСВ прямые, поэтому ∠PApB+∠PCB=9Oo+9Oo=18Oo, т.е. вокруг четырехугольника ВАрРСр можно описать окружность, центр которой совпадает с серединой Оь отрезка ВР. Поскольку вершины треугольника ВАрСр лежат на этой окружности, то Оь - центр описанной окружности треугольника ВАрСр, поэтому, как было показано в самом начале решения задачи 1, прямые ВРЬ и ВОЬ образуют равные углы со сторонами АВ и СВ треугольника АВС, т.е. изогональны относительно угла АВС этого треугольника, причем ВРЬ ZCpAp. Так как РАр ∠BС и СрРь ∠BС, то РАр || СрРь. Аналогично, РСр || АрРь и, таким образом, четырехугольник РАрРьСр - параллелограмм. Поэтому точки Р и Рь симметричны относительно середины стороны СрАр треугольника АрВрСр. Точно так же точки Р и Ра Р и Рс симметричны относительно середин сторон ВрСр и АрВр соответственно, откуда следует, что треугольник РаРьРс гомотетичен серединному треугольнику треугольника АВС с центром Р и коэффициентом k=2 и, таким образом, треугольники PaPbPc и АрВрСр равны, а их стороны соответственно параллельны. Тогда прямые АРа, ВРЬ, СРс содержат высоты треугольника PaPbPc и поэтому пересекаются в одной точке.
Заметим, что если точка P лежит на описанной окружности треугольника АВС, то прямые, изогональные прямым АР, ВР, СР, параллельны.
Как известно, точка Т, из которой стороны треугольника АВС видны под равными углами в 12oo, называется точкой Торричелли этого треугольника. Для ее построения достаточно построить на сторонах АВ, ВС, СА треугольника АВС правильные треугольники АВС1, ВСА1, САВ1 внешним образом, т.е. так, чтобы точки А и А1, В и В1, С и С1 лежали по разные стороны от прямых ВС, СА, АВ и описать около треугольников окружности, которые пересекутся в точке Т (рис. 17).
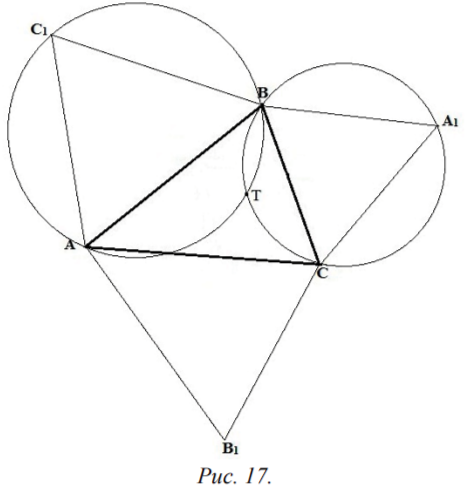
Действительно, пусть Т - точка пересечения описанных окружностей треугольников АВС. и ВСА1. Тогда
∠ATB=180о - ∠AC1B = 180о-60о=120о=180о-∠BA1C = ∠CTB
и
∠ATC=360о-∠ATB-∠CTB=360о-12Оо-12Оо=120о,
т.е. описанная окружность треугольника САВ. также проходит через точку Торричелли Т.
Заметим, что точка Торричелли существует только для треугольников, углы которых не превосходят 1200. Только такие треугольники мы и будем рассматривать в дальнейшем.
Определение 2. Треугольник ApBpCp, вершины которого совпадают с основаниями перпендикуляров, опущенных из точки Р на прямые ВС, СА, АВ, содержащие стороны треугольника АВС, называется педальным треугольником точки Р относительно треугольника АВС (рис. 18).
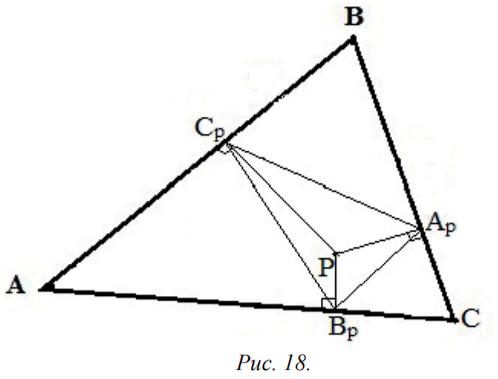
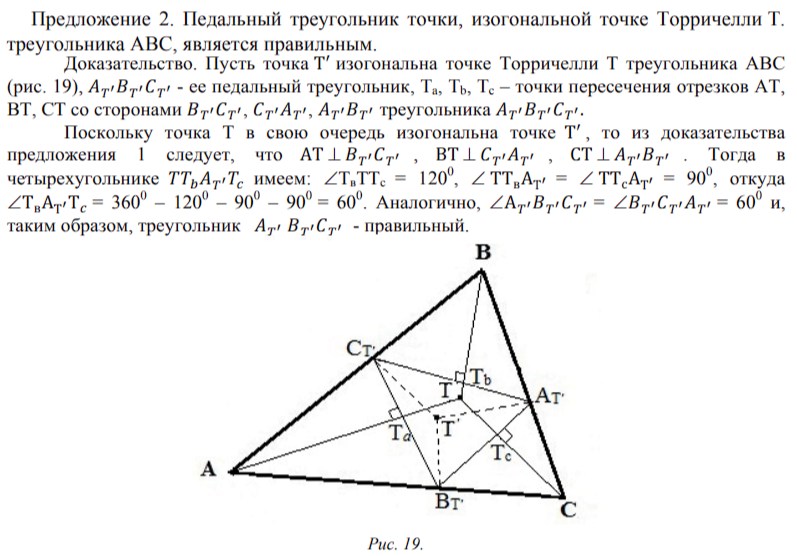
Предложение 2. Педальный треугольник точки, изогональной точке Торричелли Т. треугольника АВС, является правильным.
Предложение 3. В произвольный треугольник АВС можно вписать правильный треугольник А1В1С1 так, что его вершины А1, В1, С1 принадлежат сторонам ВС, СА, АВ треугольника АВС соответственно.
Доказательство. Выберем на сторонах АС и АВ треугольника АВС точки В' и С' соответственно (рис. 20) и построим на отрезке В'С' равносторонний
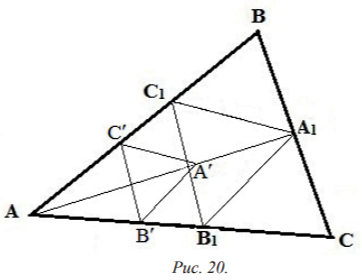
треугольник А'В'С' так, чтобы точки А и А' лежали по разные стороны от прямой В'С'. Пусть А1 - точка пересечения прямой АА' со стороной ВС.
Проведем через точку А1 прямые, параллельные прямым А'В' и А'С' и пересекающие стороны АС и ВС в точках В1 и С1 соответственно. Тогда вписанный треугольник А1В1С1 - правильный, так как его стороны соответственно параллельны сторонам правильного треугольника А'В'С'.
Из способа построения ясно, что в данный треугольник АВС можно вписать бесконечно много равносторонних треугольников А1В1С1.
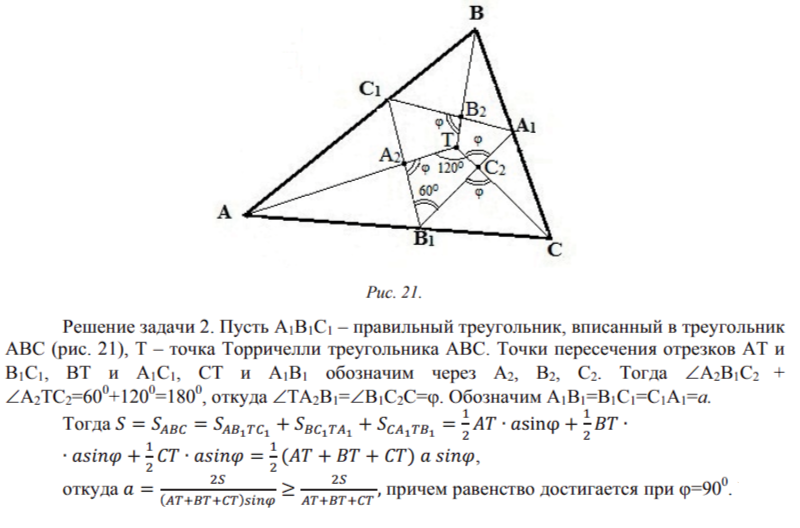
Но из доказательства предложения 2 следует, что стороны BT'CT', CT'AT', AT’BT’ педального треугольника AT’BT’CT’ точки Т', изогональной точке Торричелли Т треугольника АВС, перпендикулярны отрезкам АТ, ВТ, СТ соответственно, т.е. для правильного треугольника AT'BT'CT' угол ф=90о и, таким образом, треугольник AT'BT'CT' имеет наименьший периметр среди всех правильных треугольников, вписанных в данный треугольник АВС.
Заключение
В статье рассматривались возможные пути перевода образовательных программ по математике на современные рельсы. Авторы статьи показывают, что одним из путей модернизации математического образования является пропедевтика важных разделов высшей математики, основанная на понятиях, связанные с восприятием пространства, и интуитивно близких учащимся. В качестве конкретного примера рассматривалась пропедевтика решения экстремальных задач. Рассмотрение велось с единых позиций и основывалось на важнейшем геометрическом понятии - расстоянии. Заметим, что вопросы, связанные с последними двумя задачами статьи, уже рассматривались в работе [Куланин, 2019]. Решение всех задач проводилось с помощью опоры на интуитивно прозрачные пространственные образы. Авторы полагают, что подобную методическую работу следует проводить и в отношении другой актуальной математической тематики.
[Куланин, 2001]Nurkaeva Irina Mikhailovna, candidate of pedagogics, docent of applied Informatics and multimedia technologies, «Moscow state University of psychology and education», Moscow, Russia. E-mail: nurkaevaim@yandex.ru
[Кривошапко, 2006]Stepanov Mikhail Evgrafovich, candidate of pedagogics, docent of the Department of applied mathematics, «Moscow state University of psychology and education», Moscow, Russia. E-mail: mestepanov@yandex.ru