Обобщение неэлементарных линейных регрессий

Ранее автором была разработана неэлементарная линейная регрессия, состоящая из линейной части и всех возможных комбинаций бинарных операций min и max. Данная статья посвящена её обобщению. Впервые введена неэлементарная линейная регрессия с линейной частью и всеми возможными комбинациями бинарных, тернарных, ..., l-арных операций min и max. Предложенная модель обобщает как линейную регрессию, так и функцию Леонтьева, и может эффективно применяться как для прогнозирования, так и для интерпретации функционирования объекта исследования. Разработан алгоритм оценивания с помощью метода наименьших квадратов неэлементарных линейных регрессий без линейной части и с l-арной операцией min (max), т.е. регрессий со спецификацией в виде функции Леонтьева. Суть алгоритма состоит в формировании множества возможных значений угловых коэффициентов, из которого выбирается точка с минимальной величиной суммы квадратов остатков. Идентифицирована система линейных неравенств, позволяющая формировать такое множество. С помощью алгоритма построена модель валового регионального продукта Иркутской области и дана её интерпретация.

Введение

В настоящее время машинное обучение [1,2], вероятно, самая перспективная область искусственного интеллекта. Предназначение машинного обучения в том, чтобы запрограммировать искусственный интеллект действовать как человек, или даже лучше него, при решении различных прикладных задач. Обучение осуществляется на основе больших массивов статистических данных. Как отмечено в работе [Хенрик, 2017], «машинное обучение быстро превращается в двигатель современной экономики, управляемой данными». Совсем недавно начало выделяться новое направление – интерпретируемое машинное обучение [3,4].

С помощью машинного обучения решаются различные типы задач: классификация, кластеризация, регрессия, понижение размерности данных, обнаружение аномалий и т.д. Данная статья посвящена задаче регрессии [5–7], состоящей, как правило, в прогнозировании одной или нескольких характеристик по имеющимся статистическим данным – выборке.  На сегодняшний день известно множество математических форм связи между переменными в регрессионных моделях: линейные [5–7], полиномиальные [8,9], степенные [10,11], степенно-показательные [Базилевский, 2021], линейно-логарифмические [Базилевский, 2021], логистические [13,14], функции с фиксированными пропорциями факторов (функции Леонтьева) [Клейнер, 1986] и т.д. Тем не менее, процесс поиска новых спецификаций регрессионных моделей, позволяющих извлекать новые знания о функционировании изучаемого процесса или явления, продолжается.

В работе [Базилевский, 2020] впервые было проведено смешение линейных регрессий с двухфакторными функциями Леонтьева. Полученный синтез был назван неэлементарной линейной регрессией (НЛР). В той же работе был предложен алгоритм численного оценивания НЛР с помощью метода наименьших квадратов (МНК). В [Базилевский, 2021а] были предложены алгоритмы выбора оптимальной структуры НЛР. А в [Базилевский, 2022] впервые были введены НЛР с бинарными операциями min и max:

Цель данной работы состоит в обобщении НЛР (1), в разработке алгоритма её оценивания с помощью МНК и в решении задачи моделирования валового регионального продукта (ВРП) Иркутской области.

Обобщение НЛР

НЛР с -арной операцией min (max) без линейной части

Исключение из области  области  означает, что необходимо заменить знаки всех неравенств в таблице 1 на противоположные и внести полученные неравенства в систему. Таким образом, область  представляет собой решение системы линейных неравенств, приведенных в таблице 2.

Неравенства из системы, идентифицирующей область

Заметим, что для НЛР с -арной операцией max область  будет точно такой же.

Решение системы линейных неравенств, перечисленных в таблице 2, представляет собой открытый выпуклый многогранник (симплекс) в -мерном пространстве. Поскольку в НЛР (3) отсутствует линейная часть, то все неравенства в таблице 2 можно взять нестрогими. Тогда решение будет представлять собой замкнутый выпуклый многогранник.

Таким образом, для численного оценивания с помощью МНК НЛР (3) необходимо выбрать в области  некоторое множество точек, в каждой из них найти МНК-оценки параметров  и , и выбрать оценки, при которых сумма квадратов остатков регрессии минимальна.

Стоит отметить, что схожий алгоритм оценивания функций Леонтьева можно найти в монографии [Носков, 1996]. Однако в ней область  предложено формировать как -мерный параллелепипед. Тем самым, представленный в настоящей работе алгоритм, очевидно, эффективнее с вычислительной точки зрения.

Пример

Для демонстрации предложенного математического аппарата решалась задача моделирования ВРП Иркутской области. Для этого на сайте Федеральной службы государственной статистики (https://rosstat.gov.ru/) были собраны ежегодные статистические данные за период с 2000 по 2020 гг. (таблица 3) по следующим переменным:

 – ВРП (млн руб.);

 – продукция сельского хозяйства (млн руб.);

 – инвестиции в основной капитал (млн руб.);

 – объем работ, выполненных по виду экономической деятельности «Строительство» (млн руб.).

Таблица 3

Статистические данные

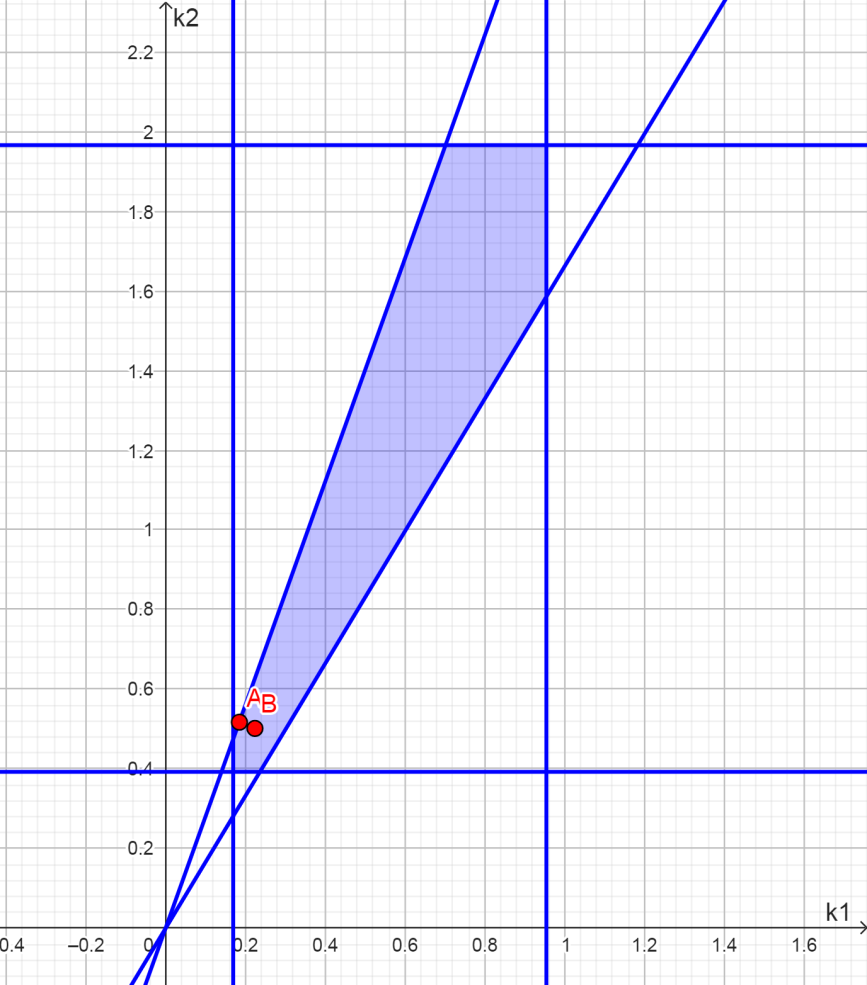
Область  решений системы линейных неравенств (6) представлена на рис. 1.

Рис. 1. Область решений системы (6)

Как следует из рис. 1, область  на плоскости представляет собой замкнутый выпуклый шестиугольник. Подчеркнём, что в системе (6) во всех неравенствах были взяты нестрогие знаки, поскольку оцениваемая НЛР представляет собой функцию Леонтьева и не содержит линейной части.

Для численного оценивания НЛР был разработан специальный скрипт на языке программирования hansl пакета Gretl. Скрипт работает по следующему алгоритму. Прямоугольник  равномерно разбивается десятью тысячами точек. В каждой такой точке и на границе области  проверяется выполнение условий . Если условия выполнены, то точка принадлежит области , поэтому для неё находятся МНК-оценки НЛР. Всего в область  попало 3422 точки. Лучшая регрессия по величине суммы квадратов остатков была зафиксирована в точке  вблизи границы области  (см. рис. 1). Полученной точке  соответствует следующая НЛР с тернарной операцией min:

  (7)

В уравнении (7) в скобках под коэффициентом 23,026 приведено значение t-критерия Стьюдента, подтверждающее значимость регрессора . Для модели (7) . Мультиколлинеарности в регрессии (7) по определению нет, поэтому все коэффициенты при переменных можно интерпретировать. Недостаток НЛР (7) в том, что практически всегда в тернарной операции min срабатывает только переменная . Так происходит в 18 наблюдениях из 21 (2000 – 2017 гг.). Переменная  срабатывает всего 2 раза (2019 и 2020 год), а переменная  – 1 раз (2018 год). Всё это сигнализирует о том, что вместо модели (7) можно было обойтись простой парной линейной регрессией  от . Действительно, такая регрессия имеет вид

(8)

для которой . Как видно, все коэффициенты и аппроксимационные характеристики моделей (7) и (8) практически не отличаются. В такой ситуации предпочтение следует отдать более простой модели (8). Заметим, что так произошло потому, что точка  (см. рис. 1) оказалась практически на границе области , на которой нет гарантии срабатывания каждой переменной на выборке хотя бы 1 раз.

После чего с помощью МНК оценивалась НЛР с тернарной операцией max и без линейной части. Для такой модели область  имеет точно такую же конфигурацию, что и на рис. 1. С помощью того же скрипта была найдена лучшая регрессия по величине суммы квадратов остатков. Она была зафиксирована в точке  внутри области  (см. рис. 1). Точке  соответствует следующая НЛР с тернарной операцией max:

 (9)

Коэффициент детерминации НЛР (9) равен 0,985536, что больше чем у любой из приведенных выше моделей (5), (7), (8).  Коэффициент при регрессоре  значим по t-критерию Стьюдента. Переменная  срабатывает 13 раз (2000 – 2006, 2008 – 2011, 2014 и 2015 годы), переменная  – 4 раза (2007, 2018 – 2020 годы), а переменная  – 4 раза (2012, 2013, 2016, 2017 годы).

Мультиколлинеарности в регрессии (9) нет, поэтому все коэффициенты при переменных можно интерпретировать. Для этого представим НЛР (9) в кусочно-заданной форме:

Тогда модель (9) можно интерпретировать следующим образом.

1. Если отношение продукции сельского хозяйства x₁ к инвестициям в основной капитал x₂ не меньше 0,223906 и отношение x₁ к объемам строительных работ x₃ не меньше 0,501629, то на ВРП оказывает влияние только продукция сельского хозяйства x₁. Причем, с увеличением x₁ на 1 млн руб. ВРП y увеличивается в среднем на 20,435 млн руб.
2. Если отношение x₁ к x₂ меньше 0,223906 и отношение x₂ к x₃ не меньше 2,240355, то на ВРП оказывают влияние только инвестиции в основной капитал x₂. Причем, с увеличением x₂ на 1 млн руб. ВРП y увеличивается в среднем на 4,576 млн руб.
3. Если отношение x₁ к x₃ меньше 0,501629 и отношение x₂ к x₃ меньше 2,240355, то на ВРП оказывают влияние только объемы строительных работ x₃. Причем, с увеличением x₃ на 1 млн руб. ВРП y увеличивается в среднем на 10,251 млн руб.

Заключение

В статье впервые введены неэлементарные линейные регрессии с линейной частью и со всеми возможными комбинациями бинарных, тернарных, ..., -арных операций min и max. Такие модели обобщают многие известные на сегодняшний день регрессионные модели, в частности, специфицированные на основе функций Леонтьева регрессии. Предложен алгоритм оценивания с помощью МНК НЛР с -арной операцией min (max). На первом шаге алгоритма строится область возможных значений угловых коэффициентов, представляющая собой решение системы линейных неравенств (таблица 2). На втором шаге из этой области выбирается точка, в которой сумма квадратов остатков НЛР минимальна. С помощью предложенного алгоритма решена задача моделирования ВРП Иркутской области. В результате была построена НЛР с тернарной операцией max, качество аппроксимации которой оказалось выше, чем у линейной регрессии. Дана интерпретация построенной модели. Таким образом, обобщенные НЛР (2) представляют собой довольно гибкий инструмент математического моделирования, просто интерпретируются и могут эффективно применяться в прогнозировании.

Очевидно, что для оценивания с помощью МНК обобщенной НЛР (2) требуется для каждой входящей в неё операции min или max формировать свою область возможных значений угловых коэффициентов, а затем в каждой из этих областей выбирать по одной точке так, чтобы минимизировать сумму квадратов остатков. Такая задача довольно сложна с вычислительной точки зрения, поэтому требует в будущем разработки специализированного программного продукта.

1. Хенрик Б., Джозеф Р., Марк Ф. Машинное обучение. СПб.: Питер, 2017. 336 с.
2. Флах П.Машинное обучение. Наука и искусство построения алгоритмов, которые извлекают знания из данных / пер. с англ. А.А. Слинкина. М.: ДМК Пресс, 2015. 400 с.
3. Molnar C.Interpretable machine learning. Lulu. com, 2020.
4. Doshi-Velez F., Kim B. Towards a rigorous science of interpretable machine learning. arXiv preprint arXiv:1702.08608. 2017.
5. Montgomery D. C., Peck E. A., Vining G. G.Introduction to linear regression analysis. John Wiley & Sons, 2021.
6. Keith T. Z.Multiple regression and beyond: An introduction to multiple regression and structural equation modeling. Routledge, 2019.
7. Gelman A., Hill J., Vehtari A. Regression and other stories. Cambridge University Press, 2020.
8. Брачунова У. В. Численное моделирование зарядного баланса легкового автомобиля // Известия Тульского государственного университета. Технические науки. 2022. № 9. С. 453–458.
9. Ярымбаш Д. С., Коцур М. И., Ярымбаш С. Т., Килимник И. М. Моделирование электромагнитных процессов при работе силовых трансформаторов под нагрузкой и в режиме холостого хода // Проблемы региональной энергетики. 2020. № 1 (45). С. 1–13.
10. Балгарина Л., Джумабаев С., Шокаманов Ю. Производственная функция Кобба–Дугласа: опыт применения в Северо-Казахстанской области // Экономическая серия вестника Евразийского национального университета имени Л.Н. Гумилева. 2022. Т. 141. № 4.
11. Чесноков Е. А. Сравнение регрессионных моделей экономического развития России // Московский экономический журнал. 2021. № 7. С. 96–105.
12. Базилевский М.П. Построение степенно-показательных и линейно-логарифмических регрессионных моделей // Проблемы управления. 2021. № 3. С. 25–32.
13. Рева С. А., Арнаутов А. В., Клиценко О. А., Петров С. Б. Прогностическая значимость логистической регрессионной модели для оценки риска рецидива у больных раком предстательной железы после радикальной простатэктомии //Research'n Practical Medicine Journal. 2022. Т. 9. № 4. С. 96–105.
14. Кокоулина М. В., Епифанова А., Пелиновский Е. Н., Куркина О. Е., Куркин А. А. Анализ динамики распространения коронавируса с помощью обобщенной логистической модели // Труды НГТУ им. Р.Е. Алексеева. 2020. № 3 (130). С. 28–41.
15. Клейнер Г. Б. Производственные функции: Теория, методы, применение. М.: Финансы и статистика, 1986. 239 с.
16. Базилевский М. П. Оценивание линейно-неэлементарных регрессионных моделей с помощью метода наименьших квадратов // Моделирование, оптимизация и информационные технологии. 2020. Т. 8. № 4 (31).
17. Базилевский М. П. Отбор информативных операций при построении линейно-неэлементарных регрессионных моделей // International Journal of Open Information Technologies. 2021. Т. 9. № 5. С. 30–35.
18. Базилевский М. П. Метод построения неэлементарных линейных регрессий на основе аппарата математического программирования // Проблемы управления. 2022. № 4. С. 3–14.
19. Носков С. И., Хоняков А. А. Программный комплекс построения некоторых типов кусочно-линейных регрессий // Информационные технологии и математическое моделирование в управлении сложными системами. 2019. № 3 (4). С. 47–55.
20. Базилевский М. П. Оценка методом наименьших квадратов простейших неэлементарных линейных регрессий с линейным аргументом в бинарной операции // Вестник кибернетики. 2022. № 4 (48). С. 69–76.
21. Носков С. И. Технология моделирования объектов с нестабильным функционированием и неопределенностью в данных. Иркутск, РИЦ ГП «Облинформпечать», 1996. 320 с.