Оптимизация выбора схемы 3D-печати функциональных объектов из композиционных материалов

Реализация приоритетных направлений развития российской экономики, цифровая трансформация производства, совершенствование и разработка новых конструкций, применяемых на отечественных предприятиях авиационной и ракетно-космической отрасли, энергетики, машиностроении и других, в значительной мере связано с использованием полимерных композиционных материалов (КМ), которые обеспечивают оптимальные физико-механические характеристики конструкций (функциональных объектов). В качестве армирующих элементов КМ широкое применение находят углеродные волокна, т.к. они обладают большой удельной прочностью. При этом механические свойства изделий существенно зависят от направления волокон. Одним из перспективных направлений изготовления объектов из КМ, позволяющим создавать конструкции сложной формы, является технология 3D-печати. Применение 3D-печати в технологии композитов в принципе позволяет получать конструкции с пространственным армированием по заданным траекториям. Это связано с тем, что для печати используется полимерный композит, армированный непрерывным углеродным волокном (CFRT). При этом возможен полный контроль над расположением волокон во время процесса печати, что позволяет располагать 100% волокон в соответствии с требуемыми условиями эксплуатации объекта. Однако практически неисследованными являются вопросы, связанные с оптимизацией процесса 3D-печати функциональных объектов из КМ методом 3D-печати CFRT в части контроля расположения волокон при печати, позволяющих учитывать критерии разрушения композита. Именно этой цели посвящена настоящая работа, в которой предлагаются общие подходы к постановке и решению задачи оптимизации выбора схемы 3D-печати.

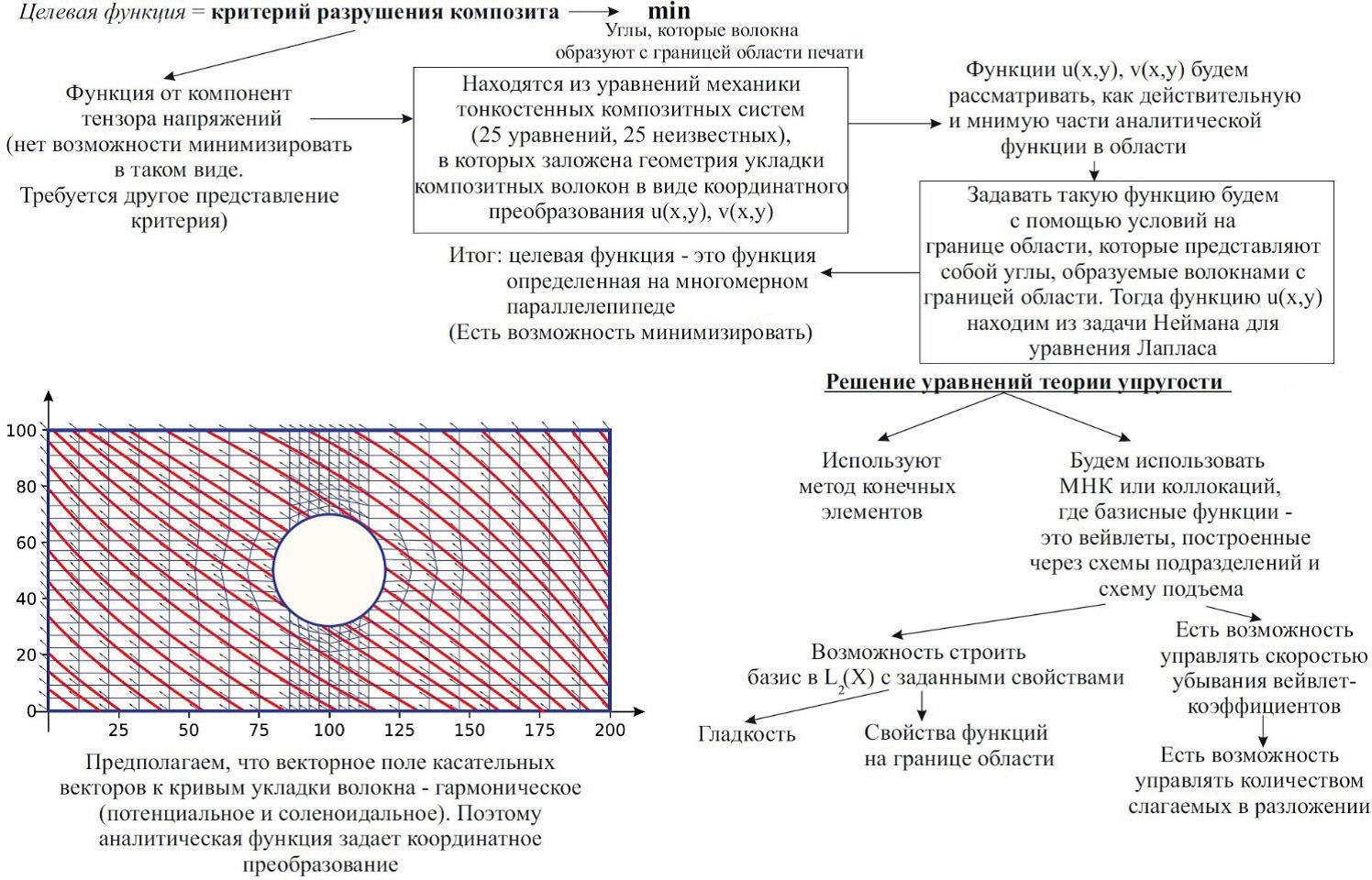
Введение

Известно, что схема укладки волокна заложена в самих уравнениях механики КМ в виде некоторой (неизвестной) локальной ортогональной системы координат. То есть найти оптимальную схему можно только из решения уравнений с разными локальными системами координат. Традиционно схемы укладки волокон рассчитываются численными методами, главным недостатком которых является большой объём и трудоёмкость вычислительного процесса. В настоящей работе предлагается схемы укладки волокон при печати моделировать с помощью аналитических функций, которые находятся из задачи Неймана для уравнения Лапласа. Работа базируется на научно-технологических решениях исследователей Yamanaka Y., Todoroki A., Ueda M., Hirano Y., Matsuzaki R., которые предложили укладывать волокна по линиям тока несжимаемой жидкости [18, 27].

Для выбора оптимальной схемы печати в качестве целевой функции можно взять любой из критериев разрушения композиционного материала [1, 12].

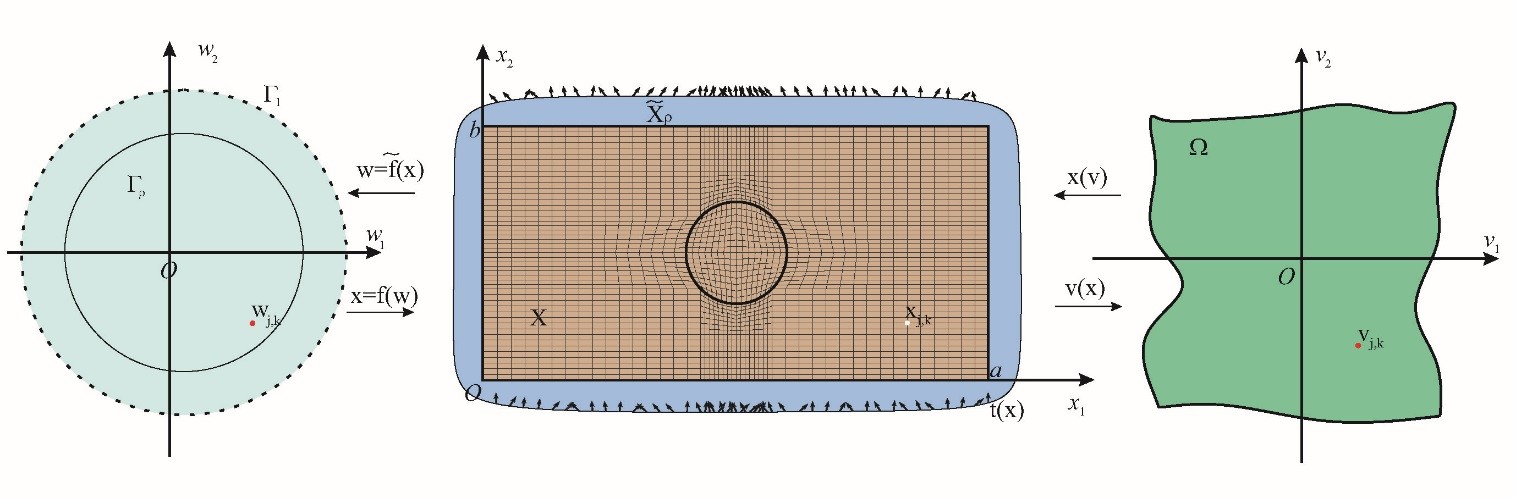
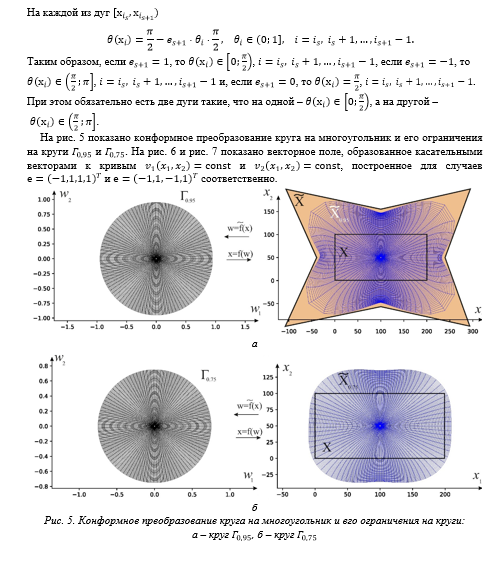
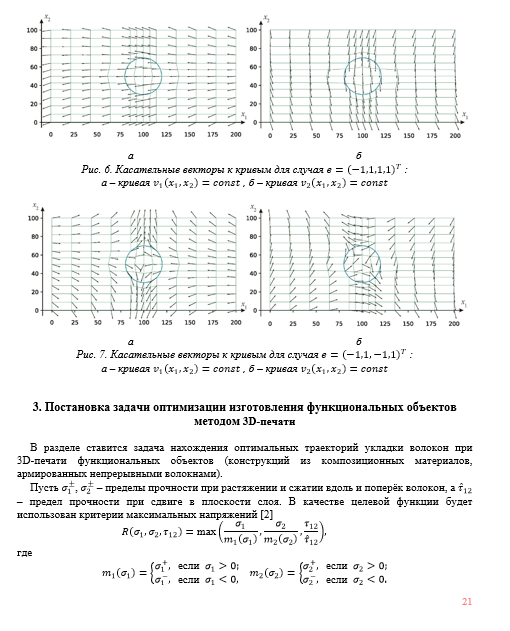
Краевые условия для задачи Неймана строятся на основе задания углов между волокнами и границей области печати. Сама задача Неймана решается посредством конформного преобразования области печати на круг, которое задаётся с помощью формулы Чизотти. Таким образом, критерий разрушения композита становится функцией от углов, образуемых волокнами с границей области печати. Минимизация целевой функции осуществляется с помощью генетического алгоритма поиска глобального минимума функции нескольких переменных. Для приближённого решения уравнений механики композиционных материалов предлагается использовать вейвлеты, построенные на основе схем подразделений и подъёма [3, 4, 10, 11, 13]. Применению вейвлетов в различных дисциплинах посвящены многочисленные исследования, в первую очередь таких авторов, как Amati G., Bujurke N., Daubechies I., Lepik, U., Mallat S., Micchelli C.A., Stollnitz E.J., Sweldens W. [9, 14, 15 – 17, 19 – 26] и др. Преимущество вейвлетов перед другими базисными функциями состоит в том, что вейвлет-коэффициенты убывают быстро, поэтому достаточно небольшого числа слагаемых в разложениях. Дополнительное преимущество вейвлетов, использующих схемы подразделений и подъёма состоит в возможности управлять формой и гладкостью базисных функций, например, можно обнулять их на выбранной области, что ещё уменьшает число слагаемых в разложении. Эти преимущества оказываются важны, т.к. при минимизации целевой функции требуется многократно решать систему уравнений в частных производных, описывающую напряжённо-деформируемое состояние конструкции [Денискина, 2022].

В данной работе предлагается общая схема решения задачи выбора оптимальной схемы 3D-печати функциональных объектов из полимерных КМ, армированных непрерывным углеродным волокном, в части контроля расположения волокон (рис. 1).

1. Элементы механики конструкций из
композиционных материалов

Представим уравнения теории упругости ортотропной среды, которые позволяют описать напряжённо-деформированное состояние широкого класса композитных систем [Васильев, 1988].

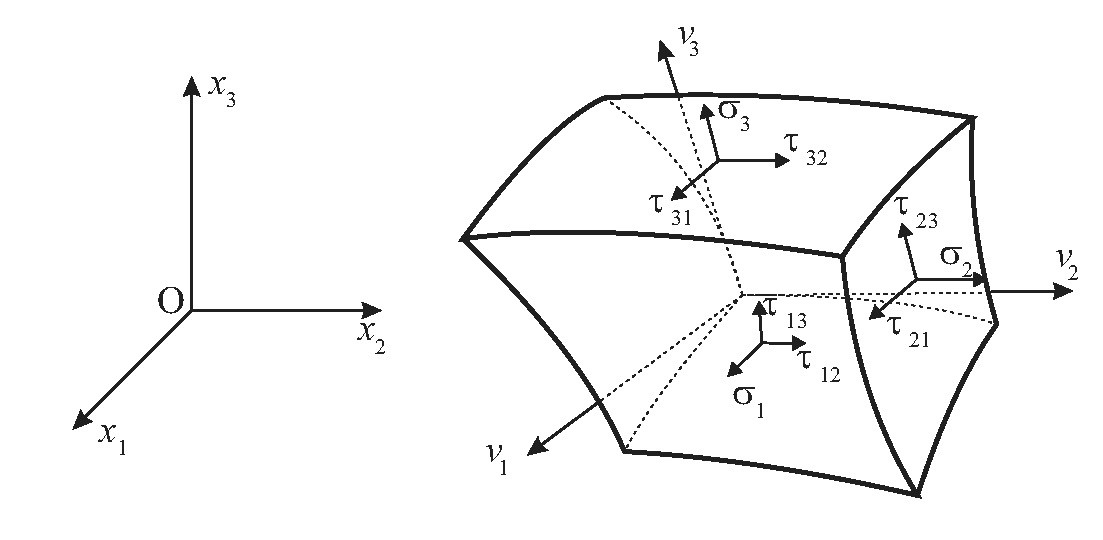
Введём декартову систему координат  и связанную с рассматриваемой средой ортогональную систему O',v1,v2,v3 криволинейных координат . Пусть соответствие между декартовой и криволинейной системами задаётся с помощью преобразования 

параметры Ламе для принятой системы координат .

Напряжённое состояние в какой-либо точке  сплошного трёхмерного тела, как известно, характеризуется тензором напряжений, который определяется девятью компонентами. Из этих компонентов три являются нормальными напряжениями, которые действуют по трём взаимно перпендикулярным направлениям координатных линий ,  и шесть – касательными напряжениями (рис. 2), действующими в трёх взаимно перпендикулярных плоскостях, являющихся касательными плоскостями в точке  к трём взаимно перпендикулярным координатным поверхностям , , .

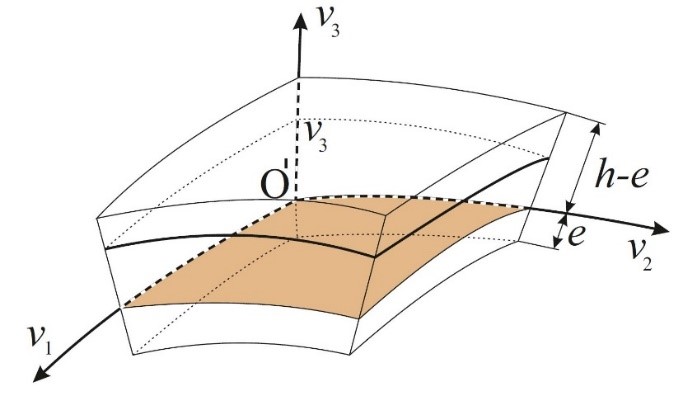
При этом ось O^' v_1 совпадает с направлением волокна, ось O^' v_3 ортогональна некоторой заданной начальной поверхности v_3=0. Обозначим A_1 (v_1,v_2 )=H_1 (v_1,v_2,0), A_2 (v_1,v_2 )=H_2 (v_1,v_2,0) – коэффициенты первой квадратичной формы начальной поверхности. Тогда, если R_1, R_2 – главные радиусы кривизны начальной поверхности, тогда коэффициенты Ламе 

вычисляются по формулам [Васильев, 1988]
H_i=A_i (1+v_3/R_i ),  H_3=1.

Будем считать, что материал не деформируется в направлении оси O^' v_3. Таким образом, изменение толщины h материала не учитывается. Поэтому ε_3=0 и μ_31=μ_32=0, E_3=∞. Следовательно, на основании этой гипотезы, получаем

Рис. 4. Преобразование множества

Следовательно,

divr=∂_1 r_1+∂_2 r_2=0.

Значит, -r_2 dx_1+r_1 dx_2 есть полный дифференциал некоторой функции v_2, определенной на X. Эта функция называется функцией тока. Таким образом, r_2=-∂_1 v_2 и r_1=∂_2 v_2. Поскольку поле потенциально, имеем

rotr=0.

Отсюда ∂_1 r_2-∂_1 r_1=0. Таким образом, выражение r_1 dx_1+r_2 dx_2 есть полный дифференциал

1. Босов, А.В., Битюков, Ю.И., Денискина, Г.Ю. О поиске оптимальной схемы 3D-печати конструкций из композиционных материалов / А.В. Босов, Ю.И. Битюков, Г.Ю. Денискина // Информатика и её применения. – 2022. – Т.16. – Вып. 1. – С. 10–19. – DOI: 10.14357/19922264220102.
2. Васильев, В.В. Механика конструкций из композиционных материалов / В.В. Васильев. – Москва: Машиностроение, 1988. – 272 с.
3. Денискина, Г.Ю. CAD/CAM/CAE-система для изготовления конструкций из волокнистых композиционных материалов методом 3D-печати / Г.Ю. Денискина // Труды МАИ. – 2022. – №126. – DOI: 10.34759/trd-2022-126-21.
4. Денискина, Г.Ю. Приближённое решение уравнений теории упругости с помощью сплайн-вейвлетов / Г.Ю. Денискина // Труды МАИ. – 2021. – №121. – DOI: 10.34759/trd-2021-121-24.
5. Денискина, Г.Ю. Программа для моделирования процесса 3D-печати CompositeCAD (подсистема CAD) / Г.Ю. Денискина // Свидетельство № 2022682105 о государственной регистрации программы для ЭВМ. – 2022.
6. Денискина, Г.Ю. Программа для моделирования процесса 3D-печати CompositeCAD (подсистема CAE) / Г.Ю. Денискина // Свидетельство № 2022682106 о государственной регистрации программы для ЭВМ. – 2022.
7. Зорич, В.А. Математический анализ: в 2 ч. / В.А. Зорич. – Изд. 3-е, испр. и доп. – Москва: МЦМНМО, 2001. – 794 с.
8. Лаврентьев, М.А., Шабат, Б.В. Методы теории функций комплексного переменного / М.А. Лаврентьев, Б.В. Шабат. – Москва: Наука, 1973. – 736 с.
9. Amati, G. The Reuse of Free-Form Surface Features: A Wavelet Approach / G. Amati, A. Liverani, G. Caligiana // Proceedings of the IASTED International Conference APPLIED SIMULATION AND MODELLING, June 28-30, 2004, Rhodes, Greece. – P. 247–252.
10. Bityukov, Y.I. Spline Wavelets Use for Output Processes Analysis of Multi-Dimensional Non-Stationary Linear Control Systems / Y.I. Bityukov, Y.I. Deniskin, G.Y. Deniskina // Journal of Physics: Conference Series. – Omsk: Institute of Physics Publishing, 2018. – P. 012018. – DOI 10.1088/1742-6596/944/1/012018.
11. Deniskina, G.Y. About Biortogonal Wavelets, Created on the Basis of Scheme of Increasing of Lazy Wavelets / G.Y. Deniskina, Y.I. Deniskin, Y.I. Bityukov // Lecture Notes in Electrical Engineering. – 2021. – Vol. 729 LNEE. – P. 173–181. – DOI 10.1007/978-3-030-71119-1_18.
12. Application of Wavelets and Conformal Reflections to Finding Optimal Scheme of Fiber Placement at 3D-Printing Constructions from Composition Materials / Yu. Bityukov, Yu. Deniskin, G. Deniskina, I.V. Potsebneva // E3S Web of Conferences: 2021. – P. 05004. – DOI 10.1051/e3sconf/202124405004.
13. Deniskina, G.Y. About Some Computational Algorithms for Locally Approximation Splines, Based on the Wavelet Transformation and Convolution / G.Y. Deniskina, Y.I. Deniskin, Y.I. Bityukov // Lecture Notes in Electrical Engineering. – 2021. – Vol. 729 LNEE. – P. 182–191. – DOI 10.1007/978-3-030-71119-1_19.
14. Bujurke, N., Shiralashetti, S., Salimath, C. An Application of Single-term Haar Wavelet Series in the Solution of Non-linear Oscillator Equations / N. Bujurke, S. Shiralashetti, C.J. Salimath // Comput. Appl. Math. – 2009. – 227. – P. 234–244.
15. Daubechies, I. A Simple Wilson Orthonormal Basis with Exponential Decay / I. Daubechies, S. Jaffard, J.L. Journe // SIAM J. Math. Anal. – 1991. – 22. – P. 554–572.
16. Daubechies, I. Orthonormal Bases of Compactly Supported Wavelets / I. Daubechies // Comm. Pure Appl. Math. – 1988. – 41. – P. 909–996.
17. Daubechies, I. Orthonormal Bases of Compactly Supported Wavelets II. Variations on a Theme / I. Daubechies // SIAM J.Math.Anal. – 1993. – 21. – P. 499–519.
18. Fiber Line Optimization in Single Ply for 3D Printed Composites / Yusuke Yamanaka, Akira Todoroki, Masahito Ueda, Yoshiyasu Hirano and Ryosuke Matsuzaki // Open Journal of Composite Materials, SCIRP. – 2016, Vol. 6, No 4. – P. 121–131.
19. Lepik, U. Application of the Haar Wavelet Transform to Solving Integral and Differential Equations / U. Lepik // Proc. Estonian Acad. Sci. Phys. Math. – 2007. – 56. – P. 28–46.
20. Lepik, U., Hein, H. Haar Wavelets with Applications / U. Lepik, H. Hein. – Springer, 2014. – 207 p.
21. Mallat, S. Multiresolution Approximation and Wavelets / S. Mallat // Trans. Amer. Math. Soc. – 1989. – 315. – P. 69–88.
22. Mallat, S. Zero-crossings of a Wavelet Transform / S. Mallat // IEEE Trans. Inform. Theory. – 1991. – 37. – P. 1019–1033.
23. Micchelli, C.A. Interpolatory Subdivision Schemes and Wavelets / C.A. Micchelli // Journal of Approximation Theory. – 1996. – Vol. 86, Issue 1. – P. 41–71.
24. Stollnitz, E.J. Wavelets for Computer Graphics: A Primer / Eric J. Stollnitz, T.D. DeRose, David H. Salesin // IEEE Computer Graphics and Applications. – 1995. – May. – 15(3). – P. 76–84 (part 1); July. – 15(4). – P. 75–85 (part 2).
25. Storn, R., Price, K. Differential Evolution – A Simple and Efficient Heuristic for Global Optimization Over Continuous Spaces / R. Storn, K. Price // Journal of Global Optimization. – 1997, No. 11. – P. 341–359.
26. Sweldens, W. The Lifting Scheme: A Custom-Design Construction of Biorthogonal Wavelets / W. Sweldens // Applied and Computational Harmonic Analysis. – 1996. –Vol.3, Issue 2. – P. 186–200.
27. Torghabehi, O.O. Developing a Computational Approach Towards a Performance Based Design and Robotic Fabrication of Fibrous Skin Structures / Omid Oliyan Torghabehi, Alireza Seyedahmadian and Wes McGee // Proceedings of the International Association for Shell and Spatial Structures (IASS) Symposium 2015, Amsterdam Future Visions, 17–20 August 2015, Amsterdam, The Netherlands. – DOI: 10.13140/RG.2.1.2324.6569.