Вычислительный эксперимент в преподавании высшей математики на примере теории чисел

Куланин Е.Д.; Степанов М.Е.

doi:10.17759/mda.2024140111

Моделирование и анализ данных
2024. Том 14. № 1. С. 170–195
doi:10.17759/mda.2024140111
ISSN: 2219-3758 / 2311-9454 (online)

Вычислительный эксперимент в преподавании высшей математики на примере теории чисел

5

Куланин Е.Д., Степанов М.Е.

Аннотация

Статья продолжает цикл методических разработок авторов [1] – [17]. В ней обсуждаются некоторые проблемы, связанные с путями повышения культуры математического мышления студентов-математиков. Авторы опираются на опыт работы на факультете информационных технологий МГППУ.

Общая информация

Ключевые слова: высшее образование, методика преподавания, параллельные вычисления, нечеткие числа

Рубрика издания: Методика преподавания

Тип материала: научная статья

DOI: https://doi.org/10.17759/mda.2024140111

Получена: 10.01.2024

Принята в печать: 25.01.2024

Для цитаты: Куланин Е.Д., Степанов М.Е. Вычислительный эксперимент в преподавании высшей математики на примере теории чисел // Моделирование и анализ данных. 2024. Том 14. № 1. С. 170–195. DOI: 10.17759/mda.2024140111

Полный текст

ВВЕДЕНИЕ

Одной из задач данной статьи является обсуждение роли эксперимента в преподавании высшей математики. Начнём статью с пространной цитаты из статьи известного отечественного математика Владимира Игоревича Арнольда [18].

«Математика — часть физики. Физика — экспериментальная, естественная наука, часть естествознания. Математика — это та часть физики, в которой эксперименты дёшевы.

Тождество Якоби (вынуждающее высоты треугольника пересекаться в одной точке) — такой же экспериментальный факт, как то, что Земля кругла (т.е. гомеоморфна шару). Но обнаружить его можно с меньшими затратами.

В середине двадцатого века была предпринята попытка разделить математику и физику. Последствия оказались катастрофическими. Выросли целые поколения математиков, незнакомых с половиной своей науки и, естественно, не имеющих никакого представления ни о каких других науках. Они начали учить своей уродливой схоластической псевдоматематике сначала студентов, а потом и школьников (забыв о предупреждении Харди, что для уродливой математики нет постоянного места под Солнцем)».

Общий смысл позиции В. И. Арнольда, с точки зрения авторов статьи таков. Математика изучает не бессодержательные абстрактные структуры, а образы реального мира. В частности, речь идёт о геометрических образах, которые характеризуют строение окружающего мира и в чём-то подобны физическим телам и силовым полям, но могут изучаться математиками без применения измерительной аппаратуры ([1]). Методы математического познания основываются на духовном созерцании образов, в известном смысле напоминающих платоновские идеи, и их логическом анализе ([10]). Если нужно охарактеризовать эти методы одним словом, то следует использовать слово «Размышление».

Однако общеизвестно то обстоятельство, что многие математические результаты могут быть получены с помощью вычислений. При этом иногда размышления и вычисления противопоставляются друг другу как антагонисты. Не вдаваясь в подробности, отметим, что математик, в отличие от инженера, должен сам разработать процедуру вычисления, включая постановку задачи, которая может быть решена вычислителем, разработку алгоритма и, наконец, анализ результатов вычисления. Таким образом, полноценное вычисление основано на размышлении. Появление компьютерной техники, несомненно, упростило вычисления с технической стороны, но не отменило их связь с размышлениями.

Учебная работа со студентами-математиками, кроме всего прочего, включает в себя развитие их интереса к математике как таковой. Добиться даже минимальных результатов в этом направлении можно, только предлагая учащимся задания, имеющие характер научного исследования. Поиск таких задач связан с определёнными трудностями. Действительно, с одной стороны задача должна быть посильной, а с другой – представлять возможности для получения новых результатов.

Авторы статьи считают, что для этих целей как раз и можно использовать задачи вычислительного характера. Данная статья посвящена рассмотрению ряда примеров таких вопросов, связанных с теорией чисел. В дальнейшем предполагается также и написание статей, которые касаются вычислений в общей алгебре, геометрии, математическом анализе и т. д.

ВЫЧИСЛИТЕЛЬНЫЙ ИНСТРУМЕНТАРИЙ

Проведение вычислений в современных условиях предполагает использование электронных вычислительных устройств. Это в высшей степени облегчает работу вычислителя. Однако, как известно, повсеместный отказ от ручных вычислений имеет ряд важных негативных последствий. Прежде всего, речь идёт об ухудшении мыслительных способностей, в том числе и студентов. По этой причине желательно использовать вычислительные задания, при выполнении которых студент должен использовать ручной, а порой даже устный счёт.

Таким образом, кроме компьютерных вычислений в данной статье будут рассматриваться и вычисления устные. Конечно, возникает вопрос о том, можно ли в современных условиях заставить студента отказаться даже от калькулятора? Сделать это можно только, наложив ограничения на результат вычислений.

Перечислим теперь те три вида вычислений, которые будут использованы далее при проведении вычислительных экспериментов.

Ручные и устные вычисления.
Вычисления с помощью электронных таблиц Excel.
Вычисления с помощью программ, написанных на языке программирования Small Basic.

Приведём примеры заданий, естественным образом решаемых одним из перечисленных видов вычислений.

Ручные и устные вычисления

Обсуждение вычислительного метода. Для извлечение квадратного корня из некоторого числа рассмотрим известную формулу сокращённого умножения

{(a + b)}^{2} = a^{2} + 2 ab + b^{2}

. Считая, что b мало, можно отбросить

b^{2}

и получить приближённую формулу

{(a + b)}^{2} \approx a^{2} + 2 ab

. Отсюда следует, что

\sqrt{a^{2} + 2 ab} \approx a + b

. Предположим, что нужно вычислить корень из числа c. Пусть a – приближённое значение корня из c, тогда можно положить, что

c = a^{2} + 2 ab

. Это позволяет вычислить параметр b. Но, зная его, можно получить и приближённое значение квадратного корня, равное

a + b

.

Задание 1. Вычислить приближённое значение

\sqrt{5}

. При этом требуется получить результат в виде обыкновенной дроби без использования калькулятора.

Решение. По условию c = 5. На роль a естественно выбрать число 2 (поскольку 22

\approx 5 .

Вычислим параметр b. Поскольку

c = a^{2} + 2 ab

, то

b = \frac{c - a^{2}}{2 a}

. В нашем конкретном случае

b = \frac{5 - 4}{4} = \frac{1}{4}

. Таким образом,

\sqrt{5} \approx 2 + \frac{1}{4} = \frac{9}{4}

.

Проведём проверку: (

\frac{9}{4}^{2} = \frac{81}{16} \approx 5.

Задание 2. Как получить более точное значение корня?

Решение. В качестве а следует взять полученное ранее приближение квадратного корня из 5.

Задание 3. Вычислить более точное значение

\sqrt{5}

.

Возможное развитие данной темы, в том числе и теоретическое, связано с разработкой аналогичных методов извлечения корней любых степеней с помощью усечения бинома Ньютона до двух слагаемых.

Вычисления с помощью электронных таблиц Excel

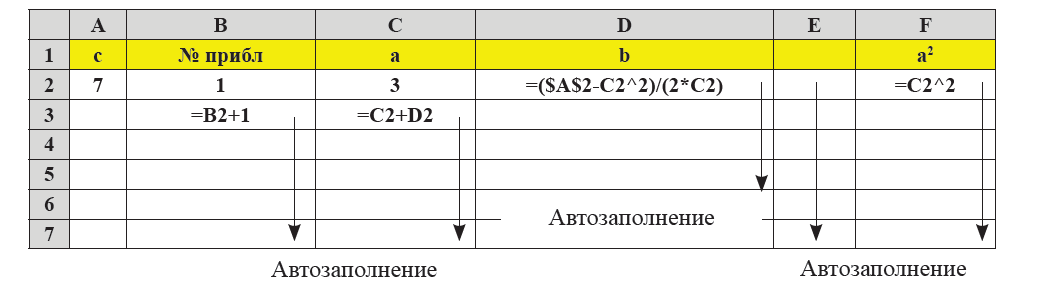
Задание 4. Вычислить, используя описанный выше способ, несколько последовательных приближений квадратного корня из какого-либо числа.

Решение. Главная задача состоит в разработке вычислительной схемы, которая будет реализована в Excel. Структура схемы показана на рисунке 1. В конкретном примере будет извлечён квадратный корень из

c =

7.

Для того, чтобы начать вычисление, необходимо выбрать исходное приближение а для квадратного корня. Это делается вычислителем. При этом на роль а2 следует выбрать ближайший к

c

квадрат натурального числа. В нашем случае

a^{2} =

9.

	A	B	C	D	E	F
1	c	№ прибл	a	b		a2
2	7	1	3	=($A$2-C2^2)/(2*C2)		=C2^2
3		=B2+1	=C2+D2
4
5
6
7

Рисунок 1

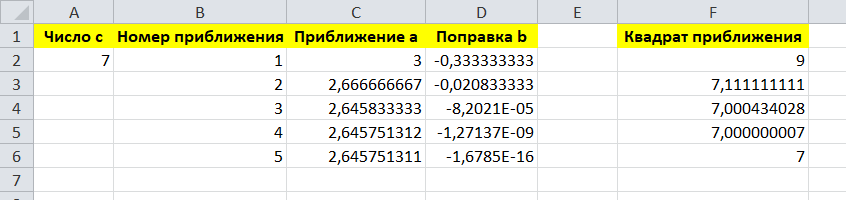
Результаты вычислений показаны на рисунке 2.

Рисунок 2

Вычисления с помощью компьютерной программы.

Задание 5. Написать программу, которая позволяет вычислить достаточно точное значение квадратного корня из какого-либо числа.

Решение. Программа соответствует вычислительной схеме, которая была реализована в Excel.

'Число

c = 29

'Степень корня

n = 2

'Исходное приближение

a = 5

'Число приближений

m = 5

'Вычислительный цикл

For i = 1 To 5

a1 = Math.Power(a,n)

a2 = Math.Power(a,n - 1)

b = (c - a1)/(n*a2)

a = a + b

'Печать очередного приближения

GraphicsWindow.DrawText(50, i*50, a)

EndFor

'Проверка результата

GraphicsWindow.DrawText(50, i*50 + 50, Math.Power(a,n))

Результаты работы программы приведены на рисунке 3.

Рисунок 3

Важной теоретической задачей в рамках данной тематики, которую можно предложить студентам, является сравнение предлагаемого способа извлечения корней с вычислениями, основанными на использовании дифференциала.

Наши вычислительные примеры можно отнести не столько к теории чисел, сколько к методам вычислений. Перейдём теперь к чисто теоретико-числовым задачам.

ДЕЛИМОСТЬ ЧИСЕЛ

Важнейшие задачи теории чисел связаны с вопросами делимости натуральных чисел. По этой причине на первое место при вычислениях должны выйти соответствующие задачи.

Задание 6. Написать программу, которая выполняет деление с остатком одного натурального числа на другое.

Решение. Пусть в программе требуется разделить число

n

на число

m

. Для этого нужно выполнить деление в поле рациональных чисел и округлить частное, до ближайшего натурального числа меньшего, чем частное. В языке Small Basic для такого округления используется функция Math.Floor(«переменная»).

'Делимое

n = 1097

GraphicsWindow.DrawText(100, 50, "Делимое равно " + n)

'Делитель

m = 19

GraphicsWindow.DrawText(100, 70, "Делитель равен " + m)

'Округление частного

p = Math.Floor(n/m)

'Получение остатка

r = n - m*p

'Печать результата

GraphicsWindow.DrawText(100, 90, "Частное равно " + p)

GraphicsWindow.DrawText(100, 110, "Остаток равен " + r)

'Проверка

GraphicsWindow.DrawText(100, 130, p + " * " + m + " + " + r + " = " + (p*m + r))

Задание 7. Написать программу, которая находит наибольший общий делитель (НОД) двух чисел.

Решение. Пусть в программе нужно найти НОД двух чисел

n

и

m

. Для нахождения НОД следует использовать алгоритм Евклида, который представляет собой многократное деление с остатком. Сначала большее из двух чисел делят с остатком на меньшее число. Далее, меньшее из исходных чисел делят на остаток. И далее каждый очередной делитель становится делимым, а очередной остаток делителем. Этот процесс продолжается до тех пор, пока не будет произведено деление с нулевым остатком. Тогда искомый НОД равен последнему делителю.

'Первое число

n = 77

'Второе число

m = 209

If n < m Then

buf = n

n = m

m = buf

EndIf

y = 30

r = n

While (r > 0)

'Округление частного

p = Math.Floor(n/m)

'Получение остатка

r = n - m*p

'Печать результата

GraphicsWindow.DrawText(100, y, "Частное равно " + p)

y = y + 30

GraphicsWindow.DrawText(100, y, "Остаток равен " + r)

y = y + 30

'Проверка

GraphicsWindow.DrawText(100, y, p + " * " + m + " + " + r + " = " + (p*m + r))

n = m

m = r

y = y + 30

EndWhile

GraphicsWindow.DrawText(100, y, "НОД равен " + n)

Задание 8. Написать программу, которая находит наименьшей общее кратное (НОК) двух чисел.

Решение. Имея в своём распоряжении предыдущую программу, достаточно просто написать программу для нахождения НОК. Тем не менее, полезно предлагать студентам и простые задания, связанные с вычислениями. В частности, их выполнение помогает освоить ранее разработанные вычислительные алгоритмы.

Задание 9. Написать программу, которая вычисляет теоретико-числовую функцию Эйлера.

Решение. Функция Эйлера от натурального числа

n

обозначается через

φ (n)

. По определению

φ (1) = 1

. При

n > 1

функция Эйлера равна количеству взаимно простых с

n

натуральных чисел из последовательности 1, 2, …

n - 1

. Таким образом, для вычисления функции Эйлера (в программе это значение обозначено через funk) от некоторого аргумента (в программе он обозначен через arg) нужно подсчитать количество взаимно простых с arg чисел k из последовательности 2, 3, … arg – 1. Для подсчётов используется подпрограмма, которая вычисляет соответствующие наибольшие общие делители. Если НОД k и arg равен 1, то значение funk увеличиваем на 1.

arg = 95

funk = 1

For k = 2 to arg-1

n = arg

m = k

NOD()

If n = 1 Then

funk = funk + 1

EndIf

EndFor

GraphicsWindow.DrawText(100,100,funk)

Sub NOD

r = n

While (r > 0)

p = Math.Floor(n/m)

r = n - m*p

n = m

m = r

EndWhile

EndSub

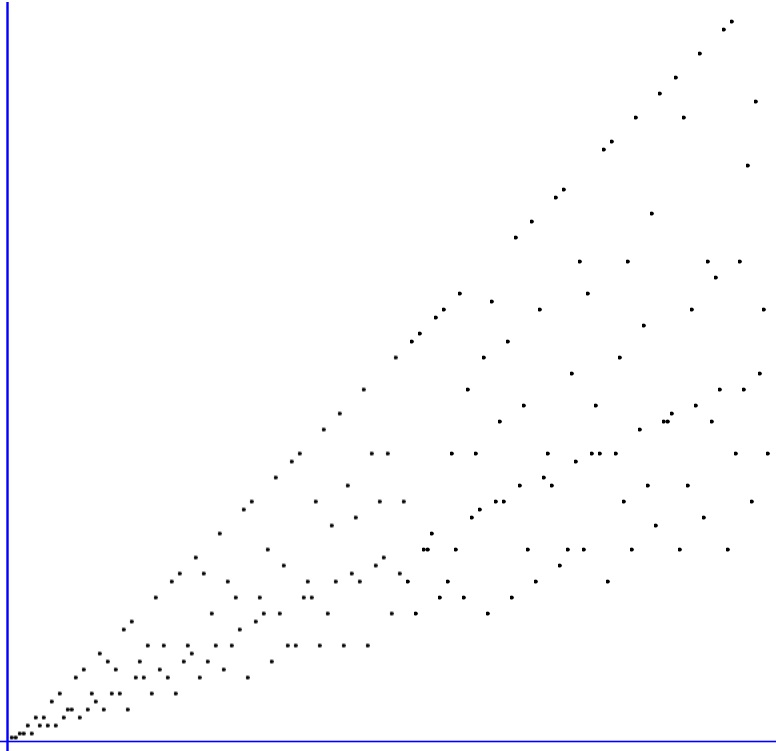
Одним из способов осмысления результатов вычислений является представление этих результатов в образной форме, например, в виде графика. Построив график функции Эйлера, можно убедиться, что её значения группируются вдоль прямых. Размышления о причинах этого факта, кроме всего прочего, потребует рассмотрения мультипликативности этой функции. Таким образом, результаты вычислений становятся поводом для теоретических построений.

Задание 10. Написать программу, которая построит график функции Эйлера.

Решение. Предыдущая программа является алгоритмическим стержнем соответствующего построения. Её результаты показаны на рисунке 4.

Sub NOD

r = n

While (r > 0)

p = Math.Floor(n/m)

r = n - m*p

n = m

m = r

EndWhile

EndSub

GraphicsWindow.Width = 800

GraphicsWindow.Height = 750

GraphicsWindow.PenColor = "blue"

GraphicsWindow.DrawLine(10,0,10,750)

GraphicsWindow.DrawLine(0,740,800,740)

GraphicsWindow.BrushColor = "black"

arg = 1

funk = 1

x = 10 + arg*4

y = 740 - funk*4

GraphicsWindow.FillEllipse(x-2,y-2,4,4)

For arg = 2 to 190

funk = 1

For k = 2 to arg-1

n = arg

m = k

NOD()

If n = 1 Then

funk = funk + 1

EndIf

EndFor

x = 10 + arg*4

y = 740 - funk*4

GraphicsWindow.FillEllipse(x-2,y-2,4,4)

EndFor

Рисунок 4

ПРОСТЫЕ ЧИСЛА

Простым числом называется натуральное число, большее, чем единица, которое делится только на себя и на единицу. Это в частности означает, что натуральное число

p

является простым тогда и только тогда, когда функция Эйлера

φ (p) = p - 1

. Таким образом, программа из задания 8 может быть использована для определения простоты натурального числа. Однако вычисления, требуемые для этой цели можно ускорить. Дело в том, что при определении простоты числа

p

нет необходимости подсчитывать количество взаимно простых с

p

чисел в интервале от 2 до

p - 1

. Достаточно показать, что делителей числа

p

в этой последовательности нет. При этом если число

p

разлагается на множители

n

и

m

(

p = n ∙ m

), то одно из этих чисел меньше или равно корню квадратному из

p

. Из этого следует, что для проверки простоты число

p

достаточно делить только на члены последовательности от двух до целой части корня квадратного из

p

.

Задание 11. Вручную определить, является ли число 131 простым.

Решение. Поскольку

11^{2} = 121

, а

12^{2} = 144

, целая часть корня квадратного из 131 равна 11. Таким образом, нужно проверить делимость числа 131 на числа из интервала от двух до одиннадцати. При этом будем использовать признаки делимости. Число 131 нечётное, значит, отбрасываем делители 2, 4, 6, 8, 10. Число 131 не делится на 3 и 9, так как сумма его цифр на эти числа не делится. Число 131 не делится на 5. Остаётся разделить с остатком 131 на 7 и 11:

131 = 140 - 14 + 5 = 20 ∙ 7 - 2 ∙ 7 + 5 = 18 ∙ 7 + 5

,

131 = 121 + 10 = 11 ∙ 11 + 10

.

Остатки от деления не равны нулю, значит, 131 не делится ни на 7, ни на 11. В итоге убеждаемся, что 131 является простым числом.

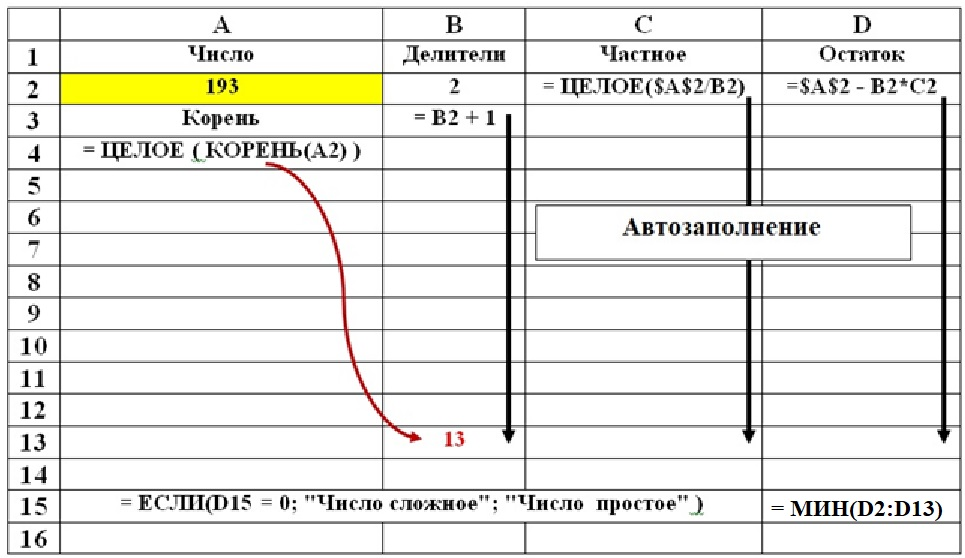
Задание 12. Разработать вычислительную схему для определения простоты числа с помощью Excel.

Решение. Предварительно нужно вычислить целую часть корня из проверяемого числа, чтобы установить количество делителей. Деление производится с остатком. Если хотя бы один остаток равен нулю, то число не является простым. Вычислительная схема показана на рисунке 5.

Рисунок 5

Задание 13. Написать программу, которая проверяет натуральное число на простоту.

Решение. В программе проверяется на простоту натуральное число

n

.

n = 1093

m = 1

prz = 0

q = Math.Floor(Math.SquareRoot(n))

For k = 2 To q

s = n/k

s1 = Math.Floor(s)

If s = s1 Then

prz = 1

EndIf

EndFor

If prz = 0 Then

GraphicsWindow.DrawText(100, 100, n + " простое число")

Else

GraphicsWindow.DrawText(100, 100, n + " сложное число")

EndIf

Простые числа образуют последовательность, которая на первый взгляд довольно хаотична, поскольку в ней наблюдается значительная неравномерность. По этой причине важной частью теории чисел является изучение распределения чисел в этой последовательности.

Прежде всего, не найдена простая аналитическая формула зависимости простого числа от его номера. По этой причине изучение простых чисел связано с вычислениями. Ими занимаются специалисты высочайшего уровня. По этой причине невозможно превзойти уже полученные результаты. Тем не менее, самостоятельное выполнение вычислений, связанных с теоретико-числовой проблематикой может оказаться очень полезным.

Одной из целей при этом может стать «личное знакомство» с натуральными числами и, в том числе, с простыми. Приведём по этому поводу цитату из книги Г. Харди [19] о индийском математике Рамануджане: «Литлвуд сказал, что каждое положительное число было одним из личных друзей Рамануджана. Я помню, как однажды собирался навестить его, когда он лежал больной в Путни. Я ехал на такси с номером 1729 и упомянул, что это число кажется мне довольно тупым и что я надеюсь, что оно не окажется неблагоприятным предзнаменованием. «Нет» – ответил он, – «это очень интересное число, это наименьшее число, которое выражается как сумма двух кубов двумя различными способами».

По этой причине продолжим работу над заданиями, связанными с теоретико-числовой проблематикой, но сделаем небольшое отступление от работы с простыми числами.

Задание 14. Найти упомянутые в цитате разложения числа 1729.

Решение. Извлечём из числа 1729 кубический корень и найдём его целую часть. Сделаем это так. Корень кубический из тысячи равен 10. Будем возводить в куб числа 11, 12 и так далее пока не получим нужный результат: 113 = 1331, 123 = 1728. Ясно, что целая часть корня кубического из 1729 равна 12. Заодно получено первое разложение: 13 + 123 = 1729.

Далее будем вычитать из 1729 кубы 11, 10 и так далее и проверять, будет ли в остатке получен ещё один куб. 1729 – 113 = 1729 – 1331 = 398 – не куб. 1729 – 103 = 729 = 93. Найдено и второе разложение: 93 + 103 = 1729.

Вернёмся к простым числам.

Задание 15. Написать программу, которая построит график последовательности занумерованных по порядку простых чисел.

Решение. График показан на рисунке 6

GraphicsWindow.Width = 300

GraphicsWindow.Height = 700

kol = 0

min = 2

max = 1200

For n = min To max

prz = 0

q = Math.Floor(Math.SquareRoot(n))

For k = 2 To q

s = n/k

s1 = Math.Floor(s)

If s = s1 Then

prz = 1

EndIf

EndFor

If prz = 0 Then

x = kol + 50

y = 650 - n/2

GraphicsWindow.FillEllipse(x - 2, y - 2, 4, 4)

kol = kol + 1

EndIf

EndFor

Рисунок 6

Задание 16. Написать программу, которая проверяет на простоту числа из некоторого интервала и подсчитывает количество простых чисел в этом интервале.

Решение. Приводимая ниже программа проверяет числа интервала натуральных чисел от

\min

до

\max

на простоту и подсчитывает их количество

kol

.

kol = 0

min = 1000

max = 1100

m = 1

For n = min To max

prz = 0

q = Math.Floor(Math.SquareRoot(n))

For k = 2 To q

s = n/k

s1 = Math.Floor(s)

If s = s1 Then

prz = 1

EndIf

EndFor

If prz = 0 Then

GraphicsWindow.DrawText(100, m*12, n + " простое число")

m = m + 1

kol = kol + 1

EndIf

EndFor

GraphicsWindow.DrawText(100, m*12 + 12, kol + " простых в интервале")

Важность простых чисел связана с тем, что с их помощью при перемножении возникают все натуральные числа, в том числе составные. Одна из первых теорем теории чисел состоит в том, что любое натуральное число больше единицы можно разложить на простые множители.

Задание 17. Используя результат задания 13, с помощью устных вычислений разложить число 1729 на простые множители.

Решение. Поскольку число, представленное в виде

a^{3} + b^{3}

, делится на

a + b

, число 1729 делится на 13 и 19. Сначала разделим его на 13. Для этого представим его в виде 1300 + 429 = 1300 + 390 + 39 = 133

∙

13. Чтобы разделить число 133 на 19, представляем его в виде 133 = 20

∙ 7 - 7

= (20

-

1)

∙ 7

= 19

∙ 7

. В итоге получено искомое разложение: 1729 = 7

∙ 13 ∙ 19

.

Задание 18. Написать программу, которая разлагает натуральное число на простые множители.

Решение. Программа делит разлагаемое на множители число

n

на числа последовательности натуральных чисел, начиная с двух. При этом деление на одно и то же число из этой последовательности производится многократно до тех пор, пока деление нацело становится невозможным. После этого производится увеличение делителя на единицу. Все делители, для которых прошло деление без остатка, фиксируются как делители числа

n

.

Может возникнуть следующий вопрос. Описанный алгоритм предполагает деление и на составные числа, например, на 4. Однако предварительно проводятся все деления на число 2. Тем самым в дальнейшем деление на все чётные числа даёт ненулевые остатки.

Число

n

в программе задано как произведение чисел, что позволяет убедиться в правильности работы программы.

GraphicsWindow.Width = 200

GraphicsWindow.Height = 700

GraphicsWindow.BrushColor = "red"

n = 11*17*19*25*27

GraphicsWindow.DrawText(50,60,n)

k = 1

d = n

m = 2

GraphicsWindow.BrushColor = "green"

While (d > 1)

p = Math.Floor(d/m)

r = d - m*p

If r = 0 Then

GraphicsWindow.DrawText(50,k*30 + 100,m)

k = k + 1

d = p

Else

m = m + 1

EndIf

EndWhile

МАКСИМАЛЬНО ПЛОТНЫЕ БЛОКИ ПРОСТЫХ ЧИСЕЛ

Последовательность простых чисел обладает свойством впечатляющей неравномерности. С одной стороны, в этой последовательности существуют сколь угодно большие пробелы, не содержащие простых чисел, то есть существуют цепочки любой длины из следующих друг за другом составных чисел [20]. С другой стороны, существуют простые числа, разность между которыми равна двум. Такие простые числа называют близнецами. Вопрос о существовании бесконечного количества близнецов не решён [21].

Однако теорема Бруна утверждает, что ряд, составленный из величин, обратных простым-близнецам, сходится, хотя ряд, составленный из величин, обратных последовательным простым числам, расходится [22]. Это означает, что близнецы среди простых чисел встречаются довольно редко.

Все близнецы, кроме пары 3 и 5, имеют вид

6 n - 1

и

6 n + 1

, так как числа с другими вычетами по модулю 6 делятся на 2 или на 3 [23]. В основу самостоятельного вычисления близнецов можно положить программу из задания 16.

Задание 19. Написать программу, которая находит числа-близнецы в заданном интервале натуральных чисел.

Решение. Программа вычисляет близнецы из интервала от 3 до 1001. Результат показан на рисунке 7.

GraphicsWindow.Width = 250

GraphicsWindow.Height = 700

m = 1

For min = 3 to 1001 step 2

kol = 0

Blizn()

EndFor

Sub Blizn

For n = min To min + 2 Step 2

prz = 0

q = Math.Floor(Math.SquareRoot(n))

For k = 2 To q

s = n/k

s1 = Math.Floor(s)

If s = s1 Then

prz = 1

EndIf

EndFor

If prz = 0 Then

kol = kol + 1

EndIf

EndFor

If kol = 2 Then

GraphicsWindow.DrawText(50, m*12, "близнецы")

GraphicsWindow.DrawText(150, m*12, min)

GraphicsWindow.DrawText(200, m*12, min + 2)

m = m + 1

EndIf

EndSub

Рисунок 7

Кроме близнецов можно рассматривать и другие плотные блоки простых чисел. Прежде всего, речь идёт о числах-триплетах. Согласно [23], триплет – это «тройка различных простых чисел, разность между наибольшим и наименьшим из которых минимальна. Наименьшими простыми числами, отвечающими заданному условию, являются — (2, 3, 5) и (3, 5, 7). Однако далее во всех остальных тройках разность между наибольшим и наименьшим членом равна шести и не может быть меньше. То есть, если обобщить, триплетом называется тройка простых чисел (2, 3, 5), (3, 5, 7),

(p, p + 2, p + 6)

или

(p, p + 4, p + 6)

.

Четверками простых чисел-близнецов (квадруплетами) называются 4 простых числа в пределах одного десятка, например, 101, 103, 107, 109. В общем виде квадруплеты задаются формулами

(p, p + 2, p + 6, p + 8)

.

Оказывается, что все такие четверки содержатся в арифметической прогрессии вида

(11 + 30 ∙ k, 13 + 30 ∙ k, 17 + 30 ∙ k, 19 + 30 ∙ k)

. Существуют четверки, у которых значения

k

отличаются на 1. Такие четверки назовем четверками-близнецами.

Задание 20. Написать программу, которая находит первые две четверки близнецов.

Решение. Первое число четвёрки при

k + 1

можно записать в виде

11 + 30 ∙ (k + 1) = 41 + 30 ∙ k

. Подобное преобразование можно проделать и для остальных трёх чисел. В результате получаем, что все восемь простых чисел из четверки близнецов являются членами арифметической прогрессии

(11 + 30 ∙ k, 13 + 30 ∙ k, 17 + 30 ∙ k, 19 + 30 ∙ k, 41 + 30 ∙ k, 43 + 30 ∙ k, 47 + 30 ∙ k, 49 + 30 ∙ k)

. Программа должна проверять на простоту именно эти числа.

Однако прямая проверка может вызвать затруднения, в том числе и психологического характера. Дело в том, что первые две четверки близнецов, скорее всего, появятся при больших значениях

k

. По этой причине проще искать четвёрки в достаточно коротких интервалах и пытаться найти две четвёрки с последовательными значениями

k

.

Программа, приводимая далее, позволяет проводить вычисления и проверкой восьмёрок (переменная diam = 8), и проверкой четвёрок (переменная diam = 4). Проверяемые интервалы имеют длину 2000. По этой причине переменной min вручную придаются значения 1, 2001, 4001, …

c[1] = 11

c[2] = 13

c[3] = 17

c[4] = 19

c[5] = 41

c[6] = 43

c[7] = 47

c[8] = 49

GraphicsWindow.Width = 300

GraphicsWindow.Height = 700

diam = 8

min = 32001

m = 1

For k = min to min + 2000

kol = 0

Blizn()

EndFor

Sub Blizn

For i = 1 To diam

n = 30*k + c[i]

prz = 0

q = Math.Floor(Math.SquareRoot(n))

For k1 = 2 To q

s = n/k1

s1 = Math.Floor(s)

If s = s1 Then

prz = 1

EndIf

EndFor

If prz = 0 Then

kol = kol + 1

EndIf

EndFor

If kol = diam Then

GraphicsWindow.DrawText(50, m*12, "четвёрки-близнецы при k =")

GraphicsWindow.DrawText(50, m*12 + 12, k)

m = m + 2

EndIf

EndSub

Результаты работы программы при diam = 4 и min = 30001, а затем при min = 32001 показаны на рисунке 8.

Рисунок 8.

Таким образом, первые две четвёрки-близнеца достигаются при

k =

33543. Следовательно, речь идёт о простых числах 1006301, 1006303, 1006307, 1006309, 1006331, 1006333, 1006337, 1006339. Понятно, что четверки-близнецы встречаются довольно редко. Тем не менее вполне возможно, что множество таких четверок-близнецов бесконечно. Конечно это гораздо более сильное предположение, чем предположение о бесконечности чисел-близнецов, т.е. пар простых чисел, разность между которыми равна двум. Очевидно, что из бесконечности множества четверок-близнецов будет следовать бесконечность множества близнецов, поскольку каждая пара четверок – близнецов состоит из четырех пар близнецов. Так в приведенном примере пару четверок (1006301, 1006303, 1006307, 1006309) и (1006331, 1006333, 1006337, 1006339) можно представить в виде объединения четырех близнецов: (1006301, 1006303), (1006307, 1006309), (1006331, 1006333) и (1006337, 1006339).

Наконец, упомянем о секступлетах (шестёрках) простых чисел. Это шестёрки простых чисел вида

(p, p + 4, p + 6, p + 10, p + 12, p + 16)

. В качестве примеров приведём две шестёрки (7, 11, 13, 17, 19, 23) и (97, 101, 103, 107, 109, 113).

ПРОСТЫЕ ЧИСЛА И МНОГОЧЛЕНЫ

Метод древнейшего доказательства бесконечности простых чисел основан на следующем рассуждении. Пусть множество простых чисел конечно. Тогда существует максимальное простое число

p

. Рассмотрим число

p! + 1

. Оно не делится ни на одно простое число, меньшее

или равное p

. Значит, оно либо является простым, либо делится на некоторое простое число, которое больше числа

p

.

Придумывая многочлен, дающий много простых значений можно использовать видоизменённую и ослабленную (по числу сомножителей) формулу: многочлен равен произведению последовательных чисел плюс простое число.

Например, многочлен Эйлера задаётся формулой

x ∙ (x + 1) + 41

.

Задание 21. Написать программу, которая вычисляет значения многочлена Эйлера и проверяет их на простоту.

Решение. Многочлен Эйлера даёт простые значения в интервале от 0 до 39, что и подтверждается работой следующей программы. Результат её работы показан на рисунке 9.

GraphicsWindow.Width = 300

GraphicsWindow.Height = 720

k = 1

For x = 1 To 39

n = x*x + x + 41

Prst()

GraphicsWindow.DrawText(50, k*18, n + txt + " при х = " + x)

k = k + 1

EndFor

Sub Prst

prz = 0

q = Math.Floor(Math.SquareRoot(n))

For z = 2 To q

s = n/z

s1 = Math.Floor(s)

If s = s1 Then

prz = 1

EndIf

EndFor

If prz = 0 Then

txt = " простое число "

Else

txt = " сложное число "

EndIf

EndSub

Рисунок 9.

Задание 22. Придумать многочлен для генерации простых чисел и провести проверку его значений на простоту.

Решение. Для многочлена-генератора выберем, например, следующую формулу

(x - 1) ∙ x ∙ (x + 1) + 23

. В программе из предыдущего задания заменим только пятую строку:

n = x*(x*x - 1) + 23

Тут, конечно, простые числа генерируются куда реже, чем у Эйлера.

ИРРАЦИОНАЛЬНЫЕ ЧИСЛА. При рассмотрении данной темы мы не будем использовать вычисления в традиционном смысле. Они будут заменены простыми манипуляциями с цифрами и блоками цифр, что в широком смысле соответствует вычислениям.

Факт наличия иррациональных чисел в качестве изучаемого объекта создаёт ряд сложностей педагогического характера. С одной стороны, без иррациональных чисел невозможно строгое построение важнейших разделов математики. С другой – иррациональные числа ускользают от непосредственного их использования. Их неизбежно округляют. Для многих людей число π – это всё-таки 3,14.

По всей видимости, существует необходимость более тесного соприкосновения студентов с иррациональными числами. При этом наиболее осязаемым является определение иррационального числа, как бесконечной непериодической дроби. Это определение открывает путь к постановке заданий, направленных на конструирование иррациональных чисел.

Нужно отметить, что многие студенты не вполне понимают, в чём состоит суть следующего задания: «Сконструировать иррациональное число». В ответ на него они называют одно из известных им иррациональных чисел, например, то же самое π.

Задание 23. Сконструировать иррациональное число.

Решение. Естественно, решений этой задачи может быть бесконечно много. Но любое из решений состоит в осмыслении понятия непериодической бесконечной дроби. Периодическая дробь с некоторого момента обретает период, то есть повторяющуюся последовательность цифр постоянной длины. Таким образом, нужна конструкция исключающая период конечной длины.

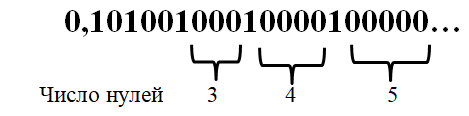
Таким образом, при конструировании иррационального числа можно использовать однородные цифровые блоки, растущей длины. Эти блоки должны разделяться отличающимся от их содержимого разделителем. Например, в качестве разделителей можно взять единицы, а в качестве равномерно растущих блоков наборы нулей. В результате будет получено следующее иррациональное число (рисунок 10).

Рисунок 10.

Идея растущих блоков может быть реализована в виде бесконечного числа вариантов, например, два вида растущих блоков из разных цифр, являющихся друг для друга разделителями:

0,122111222211111222222…

Задание 24. Задано натуральное число

n

. Сконструировать иррациональное число из

n

различных растущих блоков.

Решение. Использовать цифры n-ичной системы счисления.

Решая задание 23, студент группы 22ИТ-МО(б/о)ИСБД-1 факультета информационных технологий МГППУ Алексей Величко предложил следующий метод. Рассмотрим последовательные квадраты натуральных чисел: 1 = 12, 4 = 22, 9 = 32, 16 = 42, 25 = 52, 36 = 62, 49 = 72, 64 = 82 … После нуля и десятичной запятой выпишем последовательные цифры, образующие запись этих квадратов в десятичной системе счисления:

0,1491625364964…

Задание 25. Доказать, что получена десятичная запись иррационального числа.

Решение. В последовательность квадратов натуральных чисел входят растущие степени числа 10. Это обеспечивает присутствие в записи десятичной дроби блоков растущей длины, состоящих из нулей.

Приведённое доказательство гарантирует, что выписывание цифр последовательных натуральных чисел, а также любых их степеней приводит к получению иррациональных чисел.

Описанный метод позволяет сформулировать задачу достаточно общего характера, которую мы назовём задачей Алексея Величко.

Формулировка задачи. Дана бесконечная возрастающая последовательность натуральных чисел. После нуля и десятичной запятой выпишем последовательные цифры, образующие записи чисел этой последовательности. Установить, является ли полученная бесконечная десятичная дробь записью иррационального числа.

Каждая конкретная последовательность приводит к особой задаче. При этом такие задачи могут быть несравненно более сложными, чем в случае степеней последовательных натуральных чисел. Приведём три примера.

Пример 1. За основу взята геометрическая прогрессия

1, 2, 4 = 22, 8 = 23, 16 = 24, 25 = 25, …

Пример 2. За основу взяты числа Фибоначчи:

1, 1, 2 = 1 + 1, 3 = 1 + 2, 5 = 2 + 3…

Пример 3. За основу взяты периоды обратных для натуральных чисел величин, то есть дробей вида

{\frac{1}{n}}

. В данном случае нарушается условие монотонного роста членов исходной последовательности, но сохраняет общий характер нарастания длины блоков.

Наконец, для уяснения характера тех способов, которыми можно задавать иррациональные числа рассмотрим ещё одну конструкцию формирования десятичной дроби на основе последовательности

{a_{n}}

.

Обозначим через

\bar{a_{n}}

последовательность десятичных чисел цифр, которая описывает число

a_{n}

. Наш исходный метод состоял в последовательном построении бесконечной десятичной дроби. После n-го шага будет получена десятичная дробь 0,

\bar{a_{1}} \bar{a_{2}}

\dots

\bar{a_{n - 1}} \bar{a_{n}}

.

Вторая конструкция осуществляет в известном смысле обратное построение, при котором новые цифры вписываются сразу после запятой. В этом случае после n-го шага будет получена десятичная дробь 0,

\bar{a_{n}} \bar{a_{n - 1}}

\dots

\bar{a_{2}} \bar{a_{1}}

.

Сравним обе конструкции. И там, и там результат достигается только после бесконечного числа шагов. На каждом шагу строятся десятичные дроби равной длины. Вопрос состоит в том, приведёт ли вторая конструкция к возникновению иррационального числа? Если же не приведёт, то по какой причине?

Ответ на первый вопрос отрицательный. Причина же этого такова. В первой конструкции каждый шаг приводит к последовательному уточнению значения конструируемого числа. Таким образом, это число вычислимо. Во второй конструкции вычислимость отсутствует. Следовательно, иррациональное число ею не задаётся.

Это обсуждение показывает, что вычисления в математике имеют связь с построением исходных понятий, таких, например, как действительные числа. Надеемся, что это обстоятельство является дополнительным аргументом, обосновывающим полезность данной статьи.

Темы для самостоятельной работы студентов, связанные с теорией чисел.

Освоить определение теоретико-числовой функции Мёбиуса. Построить таблицу значений этой функции на заданном интервале.
Каждое натуральное число $n$ большее, чем 1, разлагается на простые произведение простых множителей ${p_{i}}$ , некоторые из которых могут быть равны между собой. Таким образом, $n = \prod_{i = 1}^{m} p_{i}^{k_{i}} .$ Рассмотреть функцию, которая равна числу различных простых делителей натурального числа, то есть $m$ . Построить таблицу значений этой функции на заданном интервале. Построить её график.
Рассмотреть функцию, которая равна общему числу простых делителей натурального числа, то есть $\sum_{i = 1}^{m} k_{i}$ . Построить таблицу значений этой функции на заданном интервале. Построить её график.
Получить таблицу чисел-близнецов с указанием порядковых номеров составляющих их простых чисел.
Получить таблицу триплетов.
Получить таблицу четвёрок.
Получить таблицу секступлетов.
Пусть выбрано натуральное число $n$ . Можно рассмотреть блоки простых чисел длиной $n$ . Задача исследования таких блоков состоит в решении вопроса о существовании особо плотных блоков, аналогичных ранее упомянутым близнецам, триплетам и т. д. В частности, можно решить вопрос о том, нужно ли рассматривать пропущенные в приведённой классификации пятёрки.
Сконструировать и исследовать многочлены-генераторы простых чисел.
Совершенным числом называется число, которое равно сумме своих делителей, кроме самого числа [24]. Классическим примером является шестёрка: 6 = 1 + 2 + 3. Написать программу проверки натурального числа на совершенство. Провести поиск совершенных чисел и составить таблицу.
Два числа называются дружественными числами, если сумма делителей первого числа равна второму числу и наоборот, сумма делителей второго числа равна первому числу. Примером дружественных чисел являются числа 220 и 284. Проверить это обстоятельство. Написать программу проверки наличия у данного натурального числа дружественного числа. Провести поиск дружественных чисел и составить таблицу.
Выбрать какую-нибудь числовую последовательность и для неё решить задачу Алексея Величко.

ЗАКЛЮЧЕНИЕ

Авторы надеются, что их методические идеи могут помочь молодым преподавателям в их нелёгкой работе. По этой же причине предполагается написание ещё ряда статей, связанных с вычислениями в различных областях математики.

Литература

Степанов М. Е. Образ силового поля как эвристическая модель в математике. Моделирование и анализ данных. Труды факультета информационных технологий МГППУ. – Вып. 3., 2007.
Степанов М. Е. Эрлангенская программа Клейна и геометрия треугольника. Моделирование и анализ данных. Труды факультета информационных технологий МГППУ. – 2015. №1. С.100-135.
Степанов М. Е. Эрлангенская программа Клейна и геометрия треугольника(часть вторая). Моделирование и анализ данных. Труды факультета информационных технологий МГППУ. – 2016. №1. С.60-115.
Степанов М. Е. Эрлангенская программа Клейна и геометрия треугольника Моделирование и анализ данных. Математическое образование. 2017. №3(83). С.28-42.
Степанов М. Е. Компьютерные технологии как средство приобщения учащегося к математической реальности. Моделирование и анализ данных. Научный журнал. – Вып. 1, 2018.
Куланин Е.Д., Нуркаева И.М.О двух геометрических задачах на экстремум. Математика в школе. 2019. № 4. С. 35-40.
Куланин Е.Д., Нуркаева И.М. Еще раз о задаче Мавло. Математика в школе. 2020. № 2. С. 76-79.
8.Куланин Е.Д., Степанов М. Е., Нуркаева И.М. Пропедевтика решения экстремальных задач в школьном курсе математики. Моделирование и анализ данных. 2019. № 4. С.127-144.
Куланин Е. Д., Нгуен Ву Куанг, Степанов М. Е. Осязаемая предметность с компьютерной поддержкой. Моделирование и анализ данных. Научный журнал. 2019. № 4. С.145-156.
Куланин Е.Д.,Степанов М. Е., Нуркаева И.М. Роль образного мышления в научном мышлении. Моделирование и анализ данных. 2020. Т.10. №2 С.110 - 128.
Куланин Е.Д., Степанов М. Е., Нуркаева И.М. О различных подходах к решению экстремальных задач. Моделирование и анализ данных. 2020. Т.11. №1. С.40 - 60.
Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А., Куланин Е.Д. Сборник задач по высшей математике с контрольными работами. Москва, 2013. Том 2 (8-е издание).
Степанов М.Е. Некоторые вопросы методики преподавания высшей математики. Моделирование и анализ данных. Научный журнал. – Вып. 1, 2017.
Степанов М.Е. Некоторые вопросы методики преподавания высшей математики. Моделирование и анализ данных. 2017. №1. С.54-94.
Куланин Е.Д., Степанов М. Е. Из опыта работы в режиме дистанционного обучения Моделирование и анализ данных. 2022. Т.12. №3. С.58 – 70.
Куланин Е.Д., Степанов М. Е. Всестороннее рассмотрение математических понятий как методический прием. Моделирование и анализ данных. 2022. Т.12. №4. С.67 – 84.
Куланин Е.Д., Степанов М. Е. О визуализации решений некоторых экстремальных задач. Моделирование и анализ данных. 2022. Т.12. №4. С.94 - 104.
Арнольд В. И. О преподавании математики. УСПЕХИ МАТЕМАТИЧЕСКИХ НАУК, т. 53, вып.1 (319).
Харди Г. Двенадцать лекций о Рамануджане. М., Институт компьютерных исследований. 2002.
Прахар К. Распределение простых чисел. М., Мир, 1967.
Серпинский В. Что мы знаем и чего не знаем о простых числах. М. – Л. Гос. изд. физ. – мат. литературы. 1963.
Зенкин В. И. Распределение простых чисел: Элементарные методы. Калининград, 2008.
ru.wikipedia.org › Числа-близнецы.
Депман. И. Совершенные числа. Квант, 1991, №5.

Информация об авторах

Куланин Евгений Дмитриевич, кандидат физико-математических наук, профессор, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), Москва, Россия, ORCID: https://orcid.org/0000-0001-6093-7012, e-mail: lucas03@mail.ru

Степанов Михаил Евграфович, кандидат педагогических наук, доцент, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), Москва, Россия, ORCID: https://orcid.org/0000-0003-4803-8211, e-mail: mestepanov@yandex.ru

Метрики

Просмотров

Всего: 17
В прошлом месяце: 0
В текущем месяце: 17

Скачиваний

Всего: 5
В прошлом месяце: 0
В текущем месяце: 5

PlumX

Метрики публикации