Экспертное задание нечётких строгих порядков

Смерчинская С.О.; Яманаева Р.Р.

doi:10.17759/mda.2024140204

Моделирование и анализ данных
2024. Том 14. № 2. С. 62–79
doi:10.17759/mda.2024140204
ISSN: 2219-3758 / 2311-9454 (online)

Экспертное задание нечётких строгих порядков

0

Смерчинская С.О., Яманаева Р.Р.

Аннотация

В работе представлен метод опроса экспертов для случая агрегирования нечётких предпочтений, задаваемых через попарное сравнение альтернатив. Показана возможность уменьшения числа вопросов, задаваемых экспертам при опросе. На примере разобрано взятие нечёткого транзитивного замыкания для бинарного отношения, создаваемого экспертом в ходе опроса, и за счёт этого сокращения числа сравнений.

Общая информация

Ключевые слова: выбор, эксперт, бинарная классификация, опрос, порядок, принцип транзитивности

Рубрика издания: Анализ данных

Тип материала: научная статья

DOI: https://doi.org/10.17759/mda.2024140204

Получена: 13.05.2024

Принята в печать: 27.05.2024

Для цитаты: Смерчинская С.О., Яманаева Р.Р. Экспертное задание нечётких строгих порядков // Моделирование и анализ данных. 2024. Том 14. № 2. С. 62–79. DOI: 10.17759/mda.2024140204

Полный текст

Введение

Пусть в рамках задачи группового выбора из множества альтернатив надо выбрать некоторое подмножество наилучших или расставить альтернативы по предпочтительности, с учётом советов всех заинтересованных лиц. В качестве заинтересованных лиц выступают эксперты, которые должны выразить свои мнения относительно той или иной альтернативы. При выявлении предпочтений экспертов на множестве альтернатив необходимо упрощать процедуру так, чтобы она отвечала неким интуитивным критериям достоверности, скорости и другим. Для этого надо, чтобы эксперту было как можно проще делать выбор из альтернатив.

Распространённым алгоритмом выявления предпочтений является парнодоминантный механизм выбора ([1,3]), при котором экспертам предлагается попарно сравнивать альтернативы и выбирать более предпочтительную из пары. Выбор осложняется тем, что эксперт иногда не может точно сказать, какая из альтернатив лучше. Но при этом у него есть некоторая степень уверенности в том, что выбираемая альтернатива имеет приоритет перед другой. Чтобы выразить эту степень уверенности можно использовать аппарат нечётких множеств ([6,7,8]), в частности, нечётких бинарных отношений. Такой подход может помочь получить от экспертов информацию более точно (по сравнению с чёткими бинарными отношениями) отражающую мнение эксперта и его внутреннее понимание о том, какая альтернатива лучше.

В силу того, что эксперты могут быть не знакомы с самим механизмом построения отношения (а также и агрегированного отношения ([4,5])) и могут говорить, подчас, противоречивые вещи, предлагается упростить эксперту задачу выражения мнения. Для упрощения можно сократить количество вопросов, задаваемых эксперту, так, чтобы исключить противоречия. Например, эксперт может сказать, что альтернатива А лучше Б, а Б лучше В. Если после этих двух утверждений эксперт укажет, что В лучше А, построенное на основании такого ответа отношение не будет удовлетворять условию непротиворечивости. Для того, чтобы соблюсти условие непротиворечивости предлагается после первых двух вопросов автоматически указать, что А лучше В. За счёт этого исключаются явные противоречия.

Вывод о том, что в данном примере А лучше В, делается на основании транзитивного замыкания конструируемого отношения. В статье показано, что транзитивное замыкание не обязательно вычислять после каждого вопроса, заданного эксперту (процедура взятия транзитивного замыкания требует вычислительных ресурсов), и количество выполнений этой операции можно сократить.

Благодаря предположениям выше можно добиться сокращения числа вопросов, задаваемых эксперту в ходе выявления предпочтения, а также добиться более быстрого получения непротиворечивой информации, более тонко отражающей нюансы предпочтений эксперта, с учётом силы уверенности в предоставляемом ответе при каждом сравнении альтернатив.

Проблемы, с которыми можно столкнуться, проводя опрос экспертов, связаны с психологическим аспектом человеческого мышления ([1]). Во-первых, при опросе может влиять выбор пар, предложенных эксперту для сравнения – последовательность предъявления пар может сыграть роль в итоговом предпочтении. В этом отличие от полного опроса эксперта, когда ему предлагается сравнить все возможные пары альтернатив (но в этом случае в бинарном отношении могут выявиться противоречия). Во-вторых, эксперты могут не быть в состоянии численно отразить свое мнение при сравнивании альтернатив, человеку может быть сложно выразить неформализованную, интуитивно понимаемую информацию в конкретных числах. В-третьих, каждый эксперт может иметь свою внутреннюю шкалу для задания предпочтительности, и может случиться так, что для одного из экспертов число 0.7 – это очень сильная степень уверенности, а для другого это же число выражает неярко выраженную уверенность. В этом заключаются отличия от задачи для чётких бинарных отношений.

Постановка задачи

Задано множество альтернатив

A = {a_{1}, \dots, a_{n}}

, множество экспертов

E = {E_{1}, \dots, E_{m}}

. Индивидуальное предпочтение эксперта – нечёткое отношение строгого порядка

ρ

, заданное на множестве

A

матрицей

R

предпочтений эксперта. Матрица

{\tilde{R}}^{t} = ‖ {\tilde{R}}_{ij}^{t} ‖ \in M_{n} ([0; 1]), t = 1, \dots, m

– квадратная матрица порядка

n

с элементами из

[0; 1]

. Элемент

{\tilde{R}}_{ij}^{t}

указывает с какой степенью достоверности для эксперта альтернатива

a_{i}

предпочтительнее, чем

a_{j}

. В итоге для отношений экспертов требуется построить нечёткое агрегированное отношение, являющееся нечётким строгим порядком ([4,5,9]).

Пусть экспертная информация получается в форме попарных сравнений альтернатив. На информацию и на процедуру её выявления накладываются ограничения.

Информация, полученная от каждого эксперта по алгоритму опроса, должна быть:
- - a)однородной (т.е. единообразной, представленной в одной и той же форме для каждого эксперта);
  - b)непротиворечивой;
  - c)полной и достоверной (то есть, выражающей именно собственное мнение эксперта, а не сконструированный продукт выполнения алгоритма опроса).
Должна быть возможность пересмотреть решение для одного или нескольких экспертов в случае получения неудовлетворительных результатов.
Информация должна давать возможность построить агрегированное предпочтение (в виде упорядочения альтернатив или выявления наиболее предпочтительных).

Алгоритм опроса подразумевает возможность использования процедуры согласования получаемой от экспертов информации.

При сравнении альтернатив предполагаем, что есть несколько вариантов их взаимного сопоставления:

альтернатива $a_{i}$ предпочтительнее альтернативы $a_{j}$ ;
альтернатива $a_{j}$ предпочтительнее альтернативы $a_{i}$ ;
альтернативы $a_{i}$ и $a_{j}$ несравнимы.

В таком случае можно задать асимметричное отношение (как в чётком, так и в нечётком случае). Для матрицы

{\tilde{R}}^{t} = ‖ {\tilde{R}}_{ij}^{t} ‖

предпочтений эксперта пункты будут выглядеть следующим образом:

${\tilde{R}}_{ij}^{t} > 0, {\tilde{R}}_{ji}^{t} = 0;$
${\tilde{R}}_{i j}^{t} = 0, {\tilde{R}}_{ji}^{t} > 0;$
${\tilde{R}}_{ij}^{t} = 0, {\tilde{R}}_{ji}^{t} = 0$ .

В ходе проведения опроса может возникнуть ситуация, в которой полученная от эксперта информация окажется противоречивой, т.е. в формируемом отношении предпочтения будет существовать противоречивый контур. Для того чтобы этого не случилось, необходимо к полученным в результате опроса отношениям предъявить такое естественное требование как транзитивность. Обеспечение транзитивности формируемого в ходе опроса отношения позволит, также, сократить количество задаваемых эксперту вопросов (количество сравниваемых пар альтернатив).

Например, получив информацию о том, что альтернатива

a_{1}

предпочтительнее альтернативы

a_{2}

, а альтернатива

a_{2}

предпочтительнее альтернативы

a_{3}

, по транзитивности получим:

a_{1}

предпочтительнее

a_{3}

. Если же предложить эксперту сравнить альтернативы

a_{1}

и

a_{3}

, эксперт может ответить, что

a_{3}

менее предпочтительна, чем

a_{1}

. За счёт этого получим противоречивый контур в отношении предпочтения данного эксперта.

Сокращение числа вопросов эксперту

Обеспечение транзитивности экспертного предпочтения сводится к необходимости в ходе проведения опроса к формируемой матрице смежности (она же – матрица нечёткого предпочтения)

{\tilde{R}}^{t} (t = 1, \dots, m)

, неоднократно применять процедуру взятия транзитивного замыкания и после этого сокращать количество вопросов, задаваемых эксперту, предполагая, что за счёт транзитивности выявляется необходимая информация.

Если отношение асимметричное и не содержит контуров ([2]), то при добавлении к нему свойства транзитивности (при взятии транзитивного замыкания) получим отношение строгого порядка (значок ≻ или ≺), также не содержащее контуров. В случае строгого порядка равноценность альтернатив не рассматривается, равноценные альтернативы могут быть только в нестрогом порядке (значок ≽ или ≼). Надо заметить, что в случае нестрогого порядка, при взятии транзитивного замыкания, отсутствие контуров не гарантируется.

В результате процедуры взятия транзитивного замыкания отношения для n альтернатив число вопросов с

\frac{n^{2} - n}{2}

может быть уменьшено до

n - 1

(при

n = 100

число вопросов с 4950 может сократиться вплоть до

n - 1 = 99

). Это может произойти, если, например, при сравнении альтернативы

a_{i + 1}

c

a_{i}

(

n - 1

вопрос,

i = 1, \dots, n - 1

) получим, что каждая альтернатива

a_{i + 1}

не менее предпочтительна, чем

a_{i}

. В этом случае по транзитивности, очевидно, получим, что все

n

альтернатив попарно сравнимы.

Для доказательства следующих утверждений введём определения, относящиеся к нечётким бинарным отношениям.

Пусть

μ_{ρ^{t}} = {\tilde{R}}^{t}

– матрица принадлежности нечёткого бинарного отношения (аналогичная функции принадлежности) эксперта с номером

t

.

μ_{ρ^{t}} (a_{i}, a_{j}) = {\tilde{r}}_{ij}^{t}

– значение элемента матрицы эксперта.

A = {a_{1}, \dots, a_{n}}

– заданное множество альтернатив.

Используемые в статье операции ([8]) над нечёткими множествами (в частности, бинарными отношениями) связаны со следующими функциями принадлежности

μ_{ρ} (x), x \in ρ \subseteq A \times A

.

Функция принадлежности

\bar{X}

:

μ_{\bar{X}} (x) = 1 - μ_{X} (x) .

Функция принадлежности

X \cap Y

:

μ_{X \cap Y} (x) = \min (μ_{X} (x), μ_{Y} (x)) .

Функция принадлежности

X \cup Y

:

μ_{X \cup Y} (x) = \max (μ_{X} (x), μ_{Y} (x)) .

Функция принадлежности

X - Y

:

μ_{X - Y} (x) = \max (μ_{X} (x) - μ_{Y} (x),0) .

Для матриц

{\tilde{R}}^{X}

и

{\tilde{R}}^{Y}

бинарных отношений

X

и

Y

операции будут являться поэлементными – операция выполняется для каждой пары элементов

{\tilde{R}}_{ij}^{X}

и

{\tilde{R}}_{ij}^{Y}

. Из результатов операций над элементами составляется результирующая матрица.

Композиция

ρ^{2} = ρ \circ ρ

нечетких бинарных отношений:

μ_{ρ^{2}} (x, z) = \max_{y} (\min (μ_{ρ} (x, y), μ_{ρ} (y, z))) .

Операция композиция производится над строками и столбцами подобно операции в матричном произведении по правилу «строка на столбец».

Транзитивное нечёткое бинарное отношение

ρ

– отношение, удовлетворяющее условию:

\forall (x, y), (y, z), (x, z) \in A \times A : μ_{ρ} (x, z) \geq \max_{y} (\min (μ_{ρ} (x, y), μ_{ρ} (y, z)))

или

ρ \circ ρ \subseteq ρ (ρ^{2} \subseteq ρ) .

Транзитивность является одним из основных свойств рационального отношения предпочтения

ρ

. Она означает, что если

x

не хуже

y

с достоверностью

μ_{ρ} (x, y)

а

y

не хуже

z

с достоверностью

μ_{ρ} (y, z)

, то достоверность того, что

x

не хуже

z

не может быть меньше

\min (μ_{ρ} (x, y), μ_{ρ} (y, z))

.

Транзитивное замыкание

\hat{ρ}

нечёткого бинарного отношения

ρ

:

| A | = n, (x, y) \in ρ \subseteq A \times A, \hat{ρ} = ρ \cup ρ^{2} \cup ρ^{3} \cup \dots \cup ρ^{n} .

Операция нечёткого транзитивного замыкания предполагает (для графа отношения) подсчёт максимальной пропускной способности среди всех возможных путей между альтернативами

a_{i}

и

a_{j}

– в матрице нечёткого транзитивно замкнутого отношения будет стоять это число.

Можно показать, что транзитивное замыкание нечёткого бинарного отношения без контуров может быть получено из объединения степеней с 1 по

n - 1

.

\hat{ρ} = ρ \cup ρ^{2} \cup ρ^{3} \cup \dots \cup ρ^{n - 1} .

Это связано с тем фактом, что ненулевой элемент на пересечении строки

i

и столбца

j

в матрице графа говорит о наличии пути из

a_{i}

в

a_{j}

, и если эта матрица степени

n

, то она говорит о наличии пути, состоящем из

n

шагов. Но в случае

n

альтернатив

n

шагов говорят о наличии контура, а ранее было дано предположение, что контуров в итоговом отношении не будет. Поэтому можно утверждать, что

ρ^{n}

– матрица, состоящая из нулей.

Также транзитивное замыкание можно находить по формуле Уоршалла, имеющего сложность

O (n^{3})

.

Обязательно ли применять операцию взятия транзитивного замыкания к матрице смежности формируемого отношения после каждого сравнения двух альтернатив? На этот вопрос отвечают следующие утверждения.

Замечание. Утверждения основаны на свойстве упорядоченных пар принадлежать или не принадлежать отношению. В нечётком случае отсутствие пары означает 0 в элементе матрицы смежности (так же и в чётком случае), а любое ненулевое число уже говорит о некоторой степени принадлежности отношению (присутствие упорядоченной пары в отношении). Поэтому, заменяя любое число в матрице нечёткого отношения символом единицы, можно применять утверждения также и для случая нечёткого отношения.

Утверждение 1. Можно выбрать первые

n - 1

вопросов в попарном сравнении

n

альтернатив таким образом, что при применении процедуры взятия транзитивного замыкания

n - 2

раза (после каждого вопроса, начиная со второго) или один раз после последнего, (

n - 1

)-го, вопроса получим одну и ту же матрицу смежности формируемого отношения предпочтения.

Доказательство утверждения 1. Приведем два примера таких

n - 1

вопросов:

альтернатива

a_{1}

последовательно сравнивается с остальными альтернативами

a_{2}, a_{3}, \dots, a_{n}

;

альтернатива

a_{i}

сравнивается с

a_{i + 1}

для всех

i = 1, \dots, n - 1

.

И в том, и в другом случае каждый раз в сравнении участвует новая альтернатива, которая ранее ни с какой другой альтернативой не сравнивалась. Поэтому промежуточные взятия транзитивного замыкания не требуются. Таким образом, достаточно одного взятия транзитивного замыкания вместо

n - 2

. ∎

Следующее утверждение обобщает утверждение 1 для случая задания произвольных по счету вопросов.

Пусть каждая альтернатива из подмножества

\tilde{A} = {a_{i_{1}}, a_{i_{2}}, \dots a_{i_{k}}} (\tilde{A} \subseteq A)

не сравнима ни с одной альтернативой из множества

A ∖ \tilde{A}

.

Утверждение 2. При применении процедуры взятия транзитивного замыкания

k - 2

раза после каждого сравнения произвольной альтернативы

a_{i} \in A

с альтернативами

a_{i_{1}}, \dots, a_{i_{k}}

из

\tilde{A}

или один раз после последнего,

k - 1

, вопроса получим одну и ту же матрицу смежности формируемого отношения предпочтения.

Доказательство утверждения 2. В этом утверждении, как и в предыдущем, каждый раз в сравнении участвует новая альтернатива, которая ранее ни с какой альтернативой не была сравнима. Поэтому промежуточные взятия транзитивного замыкания не требуются. Таким образом, достаточно одного взятия транзитивного замыкания вместо

k - 2

. ∎

Замечание. Процедуру взятия транзитивного замыкания, очевидно, не стоит применять и в случае, когда отношение транзитивно. Проверка транзитивности отношения 𝜌 сводится к проверке выполнения условия

ρ^{2} \subseteq ρ

и имеет небольшую вычислительную сложность

O (n^{2})

.

Замечание. Для нечётких отношений предыдущие утверждения означают, что новая добавляемая альтернатива может только добавить новый путь, следовательно, может только увеличить пропускную способность между парой вершин-альтернатив в графе отношения.

Утверждение 3. Добавление к транзитивному отношению информации о сравнении двух ранее не сравниваемых альтернатив не приводит к получению противоречивого контура.

Доказательство утверждения 3. (От противного). Пусть

ρ

– транзитивное отношение на множестве

A

, которое не содержит упорядоченных пар

a_{i}, a_{j} >

и

a_{j}, a_{i} >

. Предположим, что после добавления к

ρ

пары, например,

a_{i}, a_{j} >

, был получен противоречивый контур:

a_{i}, a_{j} >, < a_{j}, a_{j_{1}} >, \dots, < a_{j_{k}}, a_{i} >

. Но из цепочки

a_{j}, a_{j_{1}} >, \dots, < a_{j_{k}}, a_{i} >

этого контура по транзитивности

ρ

получаем

a_{j}, a_{i} > \in ρ

, а это противоречит тому, что альтернативы

a_{i}

и

a_{j}

не сравнимы по отношению

ρ

. ∎

Таким образом, процедуру взятия транзитивного замыкания первоначально достаточно применить после сравнения (

n - 1

)-й пары элементов, например, после сравнения одного из элементов со всеми остальными. Количество применений процедуры взятия транзитивного замыкания на следующих этапах зависит от числа оставшихся несравнимых альтернатив (утверждение 2).

Для определения того, что альтернатива из подмножества

\tilde{A} = {a_{i_{1}}, a_{i_{2}}, \dots a_{i_{k}}} (\tilde{A} \subseteq A)

, т.е. не сравнима ни с какой альтернативой из множества

A

, будем использовать следующее утверждение.

Пусть

\tilde{R} = ‖ {\tilde{r}}_{i j} ‖

– матрица смежности порядка n (число альтернатив) произвольного отношения 𝜌 на множестве

A

. Вектор

S = s_{1}, s_{2}, \dots, s_{n} >

–

n

-мерный вектор с компонентами, вычисляемыми по следующей формуле:

s_{i} = \sum_{j = 1}^{n} ({\tilde{r}}_{i j} + {\tilde{r}}_{ji}) .

Утверждение 4. Если

i

-й элемент вектора

S

равен нулю (

s_{i} = 0

), то альтернатива

a_{i} \in \tilde{A}

.

Доказательство утверждения 4. Действительно, если

i

-я строка и

i

-й столбец матрицы

R

содержат только нулевые элементы, то это означает, что альтернатива

a_{i}

не сравнима ни с одним из элементов множества

A

. Утверждение справедливо и для случая нечёткого отношения

ρ

. ∎

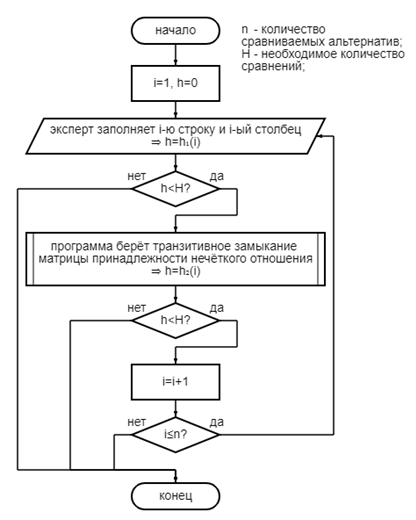
При программной реализации опроса эксперту предлагается заполнить первый столбец и первую строку матрицы с учетом асимметричности отношения (

n - 1

сравнение). Затем программа берет транзитивное замыкание полученного нечеткого отношения. Далее эксперту предлагается второй столбец и вторая строка, причем только если имеются нулевые элементы, симметричные относительно главной диагонали (будет

n - 2

или меньше сравнений). Затем программа берет транзитивное замыкание нечеткого отношения. И так далее, пока не будет достигнуто необходимое количество сравнений, в силу транзитивности или по результату выбора эксперта.

Пример построения экспертных предпочтений

Далее приведён пример построения одной матрицы сравнений при количестве альтернатив

n = 4

.

Эксперт заполняет первые строку и столбец:

μ_{ρ} = R = (\begin{matrix} 0 & 0 & 0 & 0.24 \\ 0.4 & 0 & 0 & 0 \\ 0.12 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}) .

Эксперт проделал

3 = n - 1

сравнения. Количество имеющихся сравнений: 3.

Далее проделаем операции по транзитивному замыканию:

μ_{ρ^{2}} = R^{2} = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \max (0, \min (0.24,0 .4)) \\ 0 & 0 & 0 & \max (0, \min (0.24,0 .12)) \\ 0 & 0 & 0 & 0 \end{matrix}) = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0.24 \\ 0 & 0 & 0 & 0.12 \\ 0 & 0 & 0 & 0 \end{matrix}) .

R^{3} = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}) = R^{4} .

\hat{ρ} = ρ \cup ρ^{2} \cup ρ^{3} \cup ρ^{4}, μ_{\hat{ρ}} = (\begin{matrix} 0 & 0 & 0 & 0.24 \\ 0.4 & 0 & 0 & 0.24 \\ 0.12 & 0 & 0 & 0.12 \\ 0 & 0 & 0 & 0 \end{matrix}) .

Количество имеющихся сравнений: 5.

Эксперт заполняет вторые строку и столбец:

R = (\begin{matrix} 0 & 0 & 0 & 0.24 \\ 0.4 & 0 & 0 & 0.24 \\ 0.12 & 0.8 & 0 & 0.12 \\ 0 & 0 & 0 & 0 \end{matrix}) .

Эксперт проделал

1 \leq (n - 2 = 2)

сравнения. Количество имеющихся сравнений: 6.

Далее проделаем операции по транзитивному замыканию:

R^{2} = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \max (0, \min (0.24,0 .4)) \\ \max (0, \min (0.4,0 .8)) & 0 & 0 & \max (0, \min (0.24,0 .12), \min (0.8,0 .24)) \\ 0 & 0 & 0 & 0 \end{matrix}) =

(\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0.24 \\ 0.4 & 0 & 0 & 0.24 \\ 0 & 0 & 0 & 0 \end{matrix}) .

R^{3} = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}) = R^{4} .

μ_{\hat{ρ}} = (\begin{matrix} 0 & 0 & 0 & 0.24 \\ 0.4 & 0 & 0 & \max (0.24,0 .24) \\ \max (0.12,0 .4) & 0.8 & 0 & \max (0.12,0 .24) \\ 0 & 0 & 0 & 0 \end{matrix}) = (\begin{matrix} 0 & 0 & 0 & 0.24 \\ 0.4 & 0 & 0 & 0.24 \\ 0.4 & 0.8 & 0 & 0.24 \\ 0 & 0 & 0 & 0 \end{matrix}) .

Количество имеющихся сравнений: 6.

Всего необходимо сравнений для построения строгого порядка:

\frac{n^{2} - n}{2} = \frac{16 - 4}{2} = 6

.

Пример построения агрегированного строгого порядка

Получив нечеткие строгие порядки от всех экспертов, программа приступает к выполнению алгоритма построения агрегированного строгого порядка. Алгоритм приводится в работе [4] и состоит из трех этапов.

Суммирование предпочтений.
Разрушение противоречивых контуров.
Взятие транзитивного замыкания.

Ниже приведён пример агрегирования матриц $R_{k} = ‖ {(R_{k})}_{ij} ‖, k = 1, \dots, m$ предпочтений $m$ экспертов. Пусть предпочтения экспертов уже транзитивны.

R_{1} = (\begin{matrix} 0 & 0 & 0 & 0. 3 \\ 0.99 & 0 & 0.3 & 0.3 \\ 0.99 & 0 & 0 & 0.9 \\ 0 & 0 & 0 & 0 \end{matrix}), R_{2} = (\begin{matrix} 0 & 0.8 & 0 .6 & 0 \\ 0 & 0 & 0. 6 & 0 \\ 0 & 0 & 0 & 0 \\ 0.99 & 0.9 & 0.6 & 0 \end{matrix}), R_{3} = (\begin{matrix} 0 & 1 & 0.3 & 0.9 \\ 0 & 0 & 0 & 0 \\ 0 & 0.3 & 0 & 0.9 \\ 0 & 0.3 & 0 & 0 \end{matrix}) .

1. Суммирование предпочтений.

Агрегированная матрица

R = ‖ R_{ij} ‖

предпочтений строится по формуле:

R_{ij} = \frac{1}{m} \sum_{k = 1}^{m} {(R_{k})}_{ij} .

R = (\begin{matrix} 0 & 0. 6 & 0.3 & 0.4 \\ 0.33 & 0 & 0.3 & 0.1 \\ 0.33 & 0.1 & 0 & 0.6 \\ 0.33 & 0.4 & 0.2 & 0 \end{matrix}) .

2. Разрушение противоречивых контуров.

Найдём матрицу контуров (см. [4]), используя матрицу смежности

r

агрегированного отношения. Заметим, что это для отношения

R

по свойству транзитивности на диагонали могут стоять 1, например, в силу неасимметричности, а также, если находятся контуры.

r_{K} = (Tr r) \land {(Tr r)}^{T} \land r = (\begin{matrix} 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \end{matrix}) \land (\begin{matrix} 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \end{matrix}) \land (\begin{matrix} 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \end{matrix}) = r .

Здесь «&» (как и в [4]) обозначает операцию логического «И». Для матриц это означает поэлементное применение операции.

Последовательно удаляем дуги минимального веса из всех контуров и проверяем, не исключились ли контуры.

(\begin{matrix} 0 & 0. 6 & 0.3 & 0.4 \\ 0.33 & 0 & 0.3 & 0.1 \\ 0.33 & 0.1 & 0 & 0.6 \\ 0.33 & 0.4 & 0.2 & 0 \end{matrix}) \to (\begin{matrix} 0 & 0. 6 & 0.3 & 0.4 \\ 0.33 & 0 & 0.3 & 0 \\ 0.33 & 0 & 0 & 0.6 \\ 0.33 & 0.4 & 0.2 & 0 \end{matrix}) = R, r = (\begin{matrix} 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \end{matrix}) \Rightarrow r_{K} = r .

(\begin{matrix} 0 & 0. 6 & 0.3 & 0.4 \\ 0.33 & 0 & 0.3 & 0 \\ 0.33 & 0 & 0 & 0.6 \\ 0.33 & 0.4 & 0.2 & 0 \end{matrix}) \to (\begin{matrix} 0 & 0. 6 & 0.3 & 0.4 \\ 0.33 & 0 & 0.3 & 0 \\ 0.33 & 0 & 0 & 0.6 \\ 0.33 & 0.4 & 0 & 0 \end{matrix}) = R, r = (\begin{matrix} 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 \end{matrix}) \Rightarrow r_{K} = r .

(\begin{matrix} 0 & 0. 6 & 0.3 & 0.4 \\ 0.33 & 0 & 0.3 & 0 \\ 0.33 & 0 & 0 & 0.6 \\ 0.33 & 0.4 & 0 & 0 \end{matrix}) \to (\begin{matrix} 0 & 0. 6 & 0 & 0.4 \\ 0.33 & 0 & 0 & 0 \\ 0.33 & 0 & 0 & 0.6 \\ 0.33 & 0.4 & 0 & 0 \end{matrix}) = R, r = (\begin{matrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 \end{matrix}) \Rightarrow

\Rightarrow r_{K} = (\begin{matrix} 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 \end{matrix}) \land (\begin{matrix} 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 \end{matrix}) \land (\begin{matrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 \end{matrix}) = (\begin{matrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \end{matrix}) .

(\begin{matrix} 0 & 0. 6 & 0 & 0.4 \\ 0.33 & 0 & 0 & 0 \\ 0.33 & 0 & 0 & 0.6 \\ 0.33 & 0.4 & 0 & 0 \end{matrix}) \to (\begin{matrix} 0 & 0. 6 & 0 & 0.4 \\ 0 & 0 & 0 & 0 \\ 0.33 & 0 & 0 & 0.6 \\ 0 & 0.4 & 0 & 0 \end{matrix}) = R, r = (\begin{matrix} 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \end{matrix}) = Tr r \Rightarrow

\Rightarrow r_{K} = (\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}) .

Контуров больше нет.

3. Взятие транзитивного замыкания.

Искомое отношение строгого порядка находится через создание транзитивного замыкания найденного графа с удалёнными контурами.

Tr R = Tr (\begin{matrix} 0 & 0. 6 & 0 & 0.4 \\ 0 & 0 & 0 & 0 \\ 0.33 & 0 & 0 & 0.6 \\ 0 & 0.4 & 0 & 0 \end{matrix}) = (\begin{matrix} 0 & 0. 6 & 0 & 0.4 \\ 0 & 0 & 0 & 0 \\ 0.33 & 0.4 & 0 & 0.6 \\ 0 & 0.4 & 0 & 0 \end{matrix}) .

По транзитивности было добавлено ребро

a_{3}, a_{2} >

:

\max

\max (\min (0.33, 0.6),0, 0, \min (0.6, 0.4)) = \max (0.33, 0, 0, 0.4) = 0.4 .

По матрице

Tr R

агрегированный строгий порядок будет такой:

a_{3} ≻ a_{1} ≻ a_{4} ≻ a_{2}

.

Система поддержки экспертного опроса

Рис. 1. Логическая схема алгоритма опроса

Для проведения опроса используется программная реализация алгоритма с визуализацией. Работа программы на примере, представленном выше, – на рисунках далее.

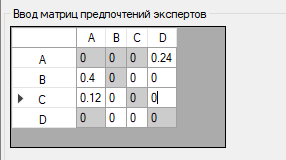
Эксперт заполняет первые столбец и строку. Например, на вопрос: «Какая степень уверенности в том, что альтернатива $A$ лучше альтернативы $D$ ?» эксперт отвечает «0.24 из 1.0». В соответствующей клетке матрицы пишется «0.24».

Рис. 2. Ввод n-1 сравнения – заполнение первых строки и столбца

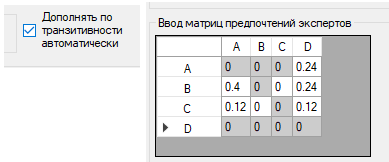
Необходимо после $n - 1$ сравнения взять транзитивное замыкание, чтобы дополнить полученную информацию непротиворечивыми выводами.

Рис. 3. Дополнение по транзитивности после n-1 сравнения

Далее заполняются незаполненные клетки во вторых столбце и строке, берётся транзитивное замыкание.

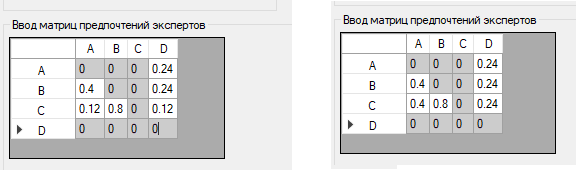
Рис. 4. Ввод оставшихся сравнений и транзитивное замыкание – получение итогового нечёткого отношения для одного эксперта

Таким образом с помощью программы достигается построение асимметричного транзитивного нечёткого отношения, соответствуюшего предпочтениям эксперта.

Программа позволяет такую же процедуру провести для нескольких экспертов, с последующим построением агрегированного отношения. Результат работы программы на примере, представленном выше – на рисунках далее.

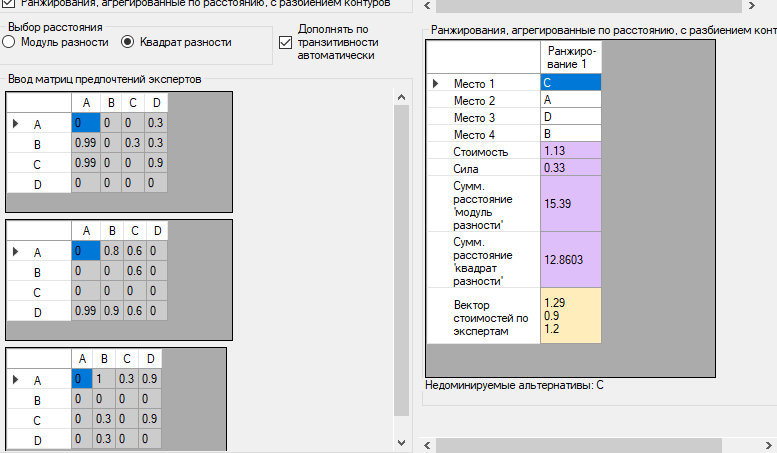
Рис. 5. Результат применения алгоритма для трёх экспертов

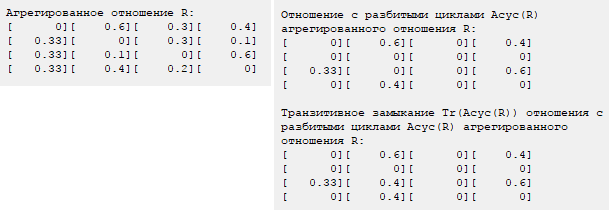
Рис. 6. Матрица агрегированного отношения R, матрицы R с разрушенными контурами и со взятым после разрушения контуров транзитивным замыканием

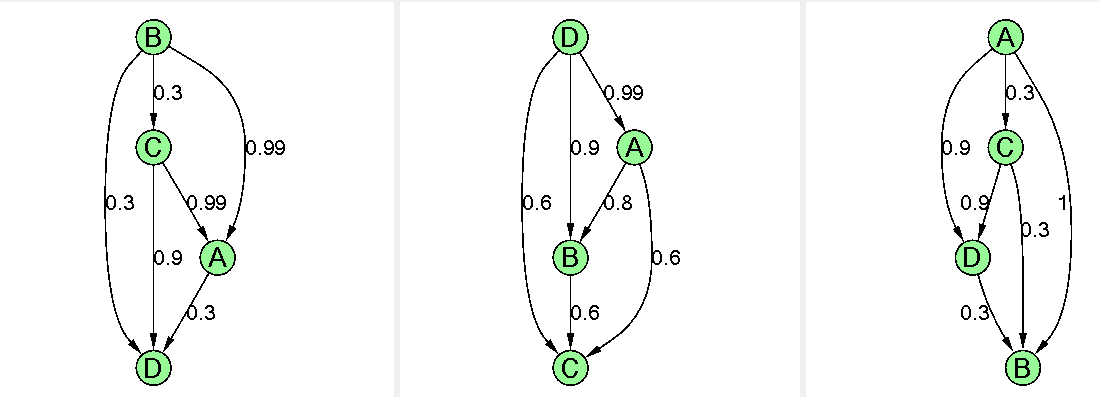
В программе имеется возможность визуализации бинарных отношений в виде графов для отражения полной картины процесса построения группового решения.

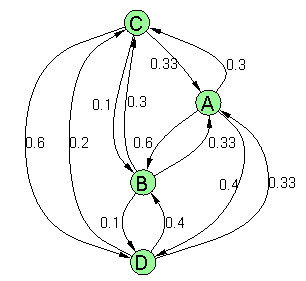
Рис. 7. Графы, соответствующие матрицам предпочтений экспертов

Рис. 8. Агрегированное отношение в виде графа

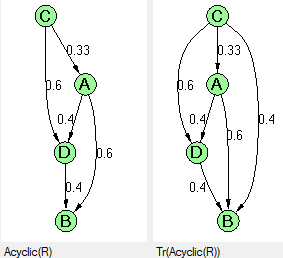
Рис. 9. Агрегированное отношение с разбитыми контурами (слева) и со взятым после этого транзитивным замыканием (справа)

Заключение

В статье разработана методика получения непротиворечивой экспертной информации, в частности нечетких отношений строгого порядка. При этом программная система позволяет значительно сократить работу эксперта, а именно не задавать вопросов, ответы на которые следуют из транзитивности нечеткого предпочтения. Приводится пример задания экспертом нечеткого отношения строгого порядка и скриншоты программы.

Литература

Вольский В.И. Процедуры голосования в малых группах // Проблемы управления. – Москва: ООО "Сенсидат-Плюс". – 2016. – С. 2-40.
Кристофидес Н. Теория графов, Алгоритмический подход. / Перевод с англ. Э.В. Вершкова, И.В. Коновальцева; Под ред. Г.П. Гаврилова. – Москва: Мир, 1978. – 432 с.
Миркин Б.Г. Проблема группового выбора. – М.: Наука, 1974. – 256 с.
Непротиворечивое агрегирование отношений строгого порядка / В.Н. Нефёдов, В.А. Осипова, С.О. Смерчинская, Н.П. Яшина // Известия высших учебных заведений. Математика. – 2018. – № 5. ‑‑С. 71‑85.
Непротиворечивое агрегирование отношений квазипорядка / В.Н. Нефёдов, С.О.Смерчинская, Н.П. Яшина // Прикладная дискретная математика. – Томск: Национальный исследовательский Томский государственный университет. – 2019. – № 45. – УДК 519.81. – С. 113-126. (Математические основы интеллектуальных систем) – DOI 10.17223/20710410/45/13
Беллман Р., Заде Л. Принятие решений в расплывчатых условиях / Беллман Р., Заде Л. [Текст] // Вопросы анализа и процедуры принятия решений. — Москва:"Мир", 1976. — С. 172-215.
Орловский С. А. Проблемы принятия решений при нечёткой информации [Текст] / С. А. Орловский — Москва: Наука, 1981 — 208 c.
Кофман А. Введение в теорию нечётких множеств [Текст] / Кофман А. — Москва: Радио и связь, 1982 — 432 c.
Трухаев Р. И. Модели принятия решений в условиях неопределённости [Текст] / Р. И. Трухаев — Москва: Наука, 1981 — 258 c.
Губко М. В. Лекции по принятию решений в условиях нечеткой информации [Текст] / Губко М. В. — Москва: ИПУ РАН, 2004. — 37 c. — Версия 1.

Информация об авторах

Смерчинская Светлана Олеговна, кандидат физико-математических наук, доцент кафедры математической кибернетики института «Компьютерные науки и прикладная математика», Московский авиационный институт (национальный исследовательский университет) (МАИ), Москва, Россия, ORCID: https://orcid.org/0000-0003-0614-1835, e-mail: svetlana_os@mail.ru

Яманаева Римма Ренатовна, студент магистратуры института «Компьютерные науки и прикладная математика», Московский авиационный институт (национальный исследовательский университет) (МАИ), Москва, Россия, ORCID: https://orcid.org/0009-0000-2874-1466, e-mail: m.e.dragon@mail.ru

Метрики

Просмотров

Всего: 0
В прошлом месяце: 0
В текущем месяце: 0

Скачиваний

Всего: 0
В прошлом месяце: 0
В текущем месяце: 0

PlumX

Метрики публикации