Введение
Внедрение цифровых систем в обучение является важнейшей вехой для решения задач и проблем современной педагогики. Автоматизация процесса контроля за успеваемостью и разработка индивидуальной траектории обучения для каждого ученика призвано улучшить качество образования и снять часть рутинной работы с преподавателя. Использование компьютеризированного адаптивного подхода к задачам психологической диагностики и обучения открыло новые возможности для эффективного обучения (Ермаков, Савенков, Шепелева, 2023). Создание новых математических моделей самообучающихся адаптивных тренажеров привело к появлению новых альтернатив современной теории тестирования (Куравский и др., 2021), а также к появлению новых программных реализаций для автоматизации и адаптации процесса обучения (Поминов, 2020; Ксемидов, Абгарян, 2024). Важность персонализации обучения и создание новых подходов к адаптивному обучению много раз отмечалась в современной литературе (Куравский и др., 2016; Кравченко и др., 2020; Амелина, 2023; Казанцева, 2024; Широколобова, 2024).
Создание механизма формирования адаптивной траектории обучения в цифровых системах призвано предоставить каждому пользователю индивидуальный путь освоения учебной дисциплины. Особую важность здесь принимает фактор предоставления учащемуся только тех задач, которые лучше всего подходят его уровню подготовки. Если пользователю будут предъявляться. одни и те же задания, которые он не может пройти на определенном этапе, то это может негативно сказаться на его мотивации.
Для каждой группы задач в цифровой системе можно определить путь от базовых понятий и заданий к более сложным. Таким образом, возможно охватить весь базовый материал, который требуется для решения выбранной группы задач. Важно отметить, что не всегда есть возможность создать путь обучения для группы особо тривиальных задач. Примером этого может служить сложение и вычитание чисел в первом классе. Если одно задание включает в себя множество математических операций, то оно уже может создать индивидуальный путь обучения для учащегося. Это нужно в ситуации, когда пользователь испытывает трудности с определенным видом математических операций, что так или иначе приводит к неверному ответу в сложных задачах. Не всегда удается интерпретировать ответ пользователя на задачу и связать его с определенной ошибкой. Поэтапное предъявление пользователю несложных для него задач на каждую математическую операцию, при возникновении проблем в задачах с множественными операциями, является одним из вариантов построения адаптивной траектории обучения. Таким образом, можно зафиксировать время выполнения одного типа математической операции, а также сам факт её успешности. Эта фиксация времени дает аналитическую информацию для педагога о том, где в рамках сложной задачи учащийся испытывает трудности.
Формирование адаптивной траектории обучения для каждого состояния марковского процесса предназначено для предоставления новых состояний и соответствующих переходов между ними в соответствии с текущими знаниями пользователя. Одним из ключевых параметров при выбранной реализации остается время пребывания в каждом из состояний. На основе неё формируется аналитическая информация, для педагога. Из-за разной степени подготовки учащихся, у большинства пользователей траектория обучения в рамках марковского процесса будет различна. Исключением здесь являются только отличники, которые могут пройти все состояния марковского процесса без выбора неверного варианта ответа, что, в результате, приведет к фиксированному количеству пройденных состояний.
Материалы и методы
Для формирования адаптивной траектории обучения в цифровой системе за математическую основу взят марковский процесс с дискретным количеством состояний и непрерывным временем (Артеменков и др., 2017). Модель (рис. 1) включает в себя состояния процесса и интенсивность переходов между ними и описывает динамику взаимодействия пользователя с системой, путем постепенного прохода пар состояний марковского процесса слева-направо. Парой состояний здесь выступает связка обычного состояния и состояния ловушки. При входе в обычное состояние происходит случайный выбор материалов в виде заданий или вопросов с последующим предъявлением его пользователю в рамках системы. При даче неверного ответа происходит переход в состояние ловушки с последующим корректирующим взаимодействием со стороны системы. Это подразумевает под собой выдачу подсказки или облегчённого варианта задания на основе интерпретации ошибочного ответа пользователя. При повторном неверном ответе пользователь остается в ловушке до дачи верного ответа на представленную задачу. Дав верный ответ, он переходит назад в обычное состояние. При даче верных ответов в обычных состояниях он переходит в следующую пару состояний. С каждой парой растет не только сложность, но и трудность представленных пользователю материалов.

Fig. 1. Markov process with discrete states and continuous time
Представленные в работах Л.С. Куравского (Куравский и др., 2017; Куравский и др., 2022) вероятности пребывания в состояниях процесса, как функции времени, определяются следующей системой обыкновенных дифференциальных уравнений Колмогорова в матричной форме:
В рамках модели подразумевается, что пары состояний будут содержать материалы, объединённые одним курсом обучения. Это позволяет автоматизировать процесс выявления пробелов в знаниях учащихся и предоставить необходимую аналитическую информацию для учителя. Данная информация формируется на основе времени пребывания пользователя в каждом из состояний марковского процесса, выданных системой типов готовности (не готов, условно готов и готов) формируемых на основе пороговых значений, а также допущенных ошибок. Каждый пользователь системы постепенно проходит пары состояний в определенном порядке слева-направо, что приводит к фиксированному порядку следования тем для каждого учащегося. Из-за этого пользователь с пробелами в знаниях в рамках выбранной темы может застрять в одной из пар состояний и находиться там до истечения времени, отведенного на прохождение всего марковского процесса. Важной информацией для аналитики здесь выступает та пара состояний где остановился пользователь и выбранные им неверные варианты ответов. К сожалению, не всегда получается по неверным вариантам ответов детально определить места где у учащегося сформировались пробелы в знаниях, что требует от учителя провести дополнительное время с ним.
Фиксированность тем для пар состояний не дает возможности по дальнейшему улучшению траектории обучения для учащихся в рамках данной модели. Формирование более адаптивной траектории обучения требует дополнения текущей модели новыми состояниями марковского процесса и переходами между ними. Новые состояния призваны хранить материалы предшествующих курсов обучения, связываясь с ловушками каждой пары состояний (рис. 2).
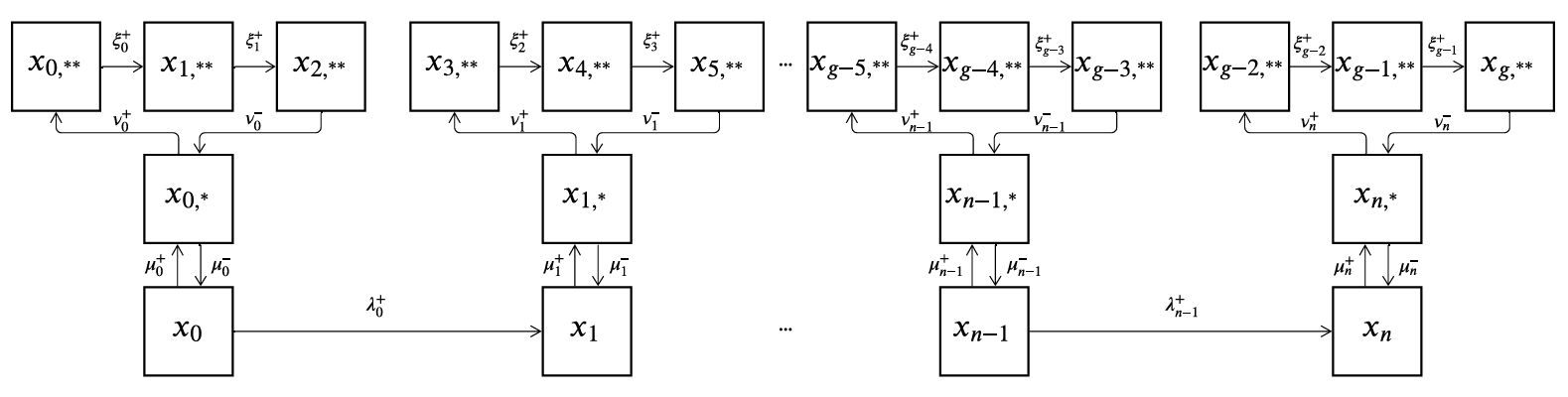
Рис. 2. Дополненный марковский процесс с дискретными состояниями и непрерывным временем
Fig. 2. Extended Markov process with discrete states and continuous time
Адаптивная траектория обучения формируется за счет третьего уровня состояний так как не каждый обучающейся будет переходить на этот уровень из-за разной подготовки. Один учащийся может плохо разбираться в теме второй пары состояний марковского процесса, а другой знать на отлично, что приведёт только к единичному переходу на третий уровень. Отличник может ни разу не перейти на третий уровень во всех парах состояний. Таким образом траектория обучения для каждого пользователя будет различна за счёт разнообразия состояний, которые они проходят. Адаптивность в рамках системы выполняется за счет предоставления пользователю состояний, которые соответствуют его текущему уровню подготовки.
Результаты
В рамках исследовательской работы был доработан прототип веб-приложения тренажера, предназначенный для обучения школьников начальных классов. Для наполнения системы были сформированы материалы на основе заданий по математике с первого по четвертый класс. Материалы для каждого учебного класса группируются по темам начиная с самых легких и заканчивая заданиями повышенной сложности. В случае если тема подразумевает наличие простых и сложных заданий одновременно, более трудные переносятся в состояние ближе к концу марковского процесса. На основе материалов для первого и второго класса были сформированы марковские процессы с 5 парами состояний и переходами между ними (рис. 3).
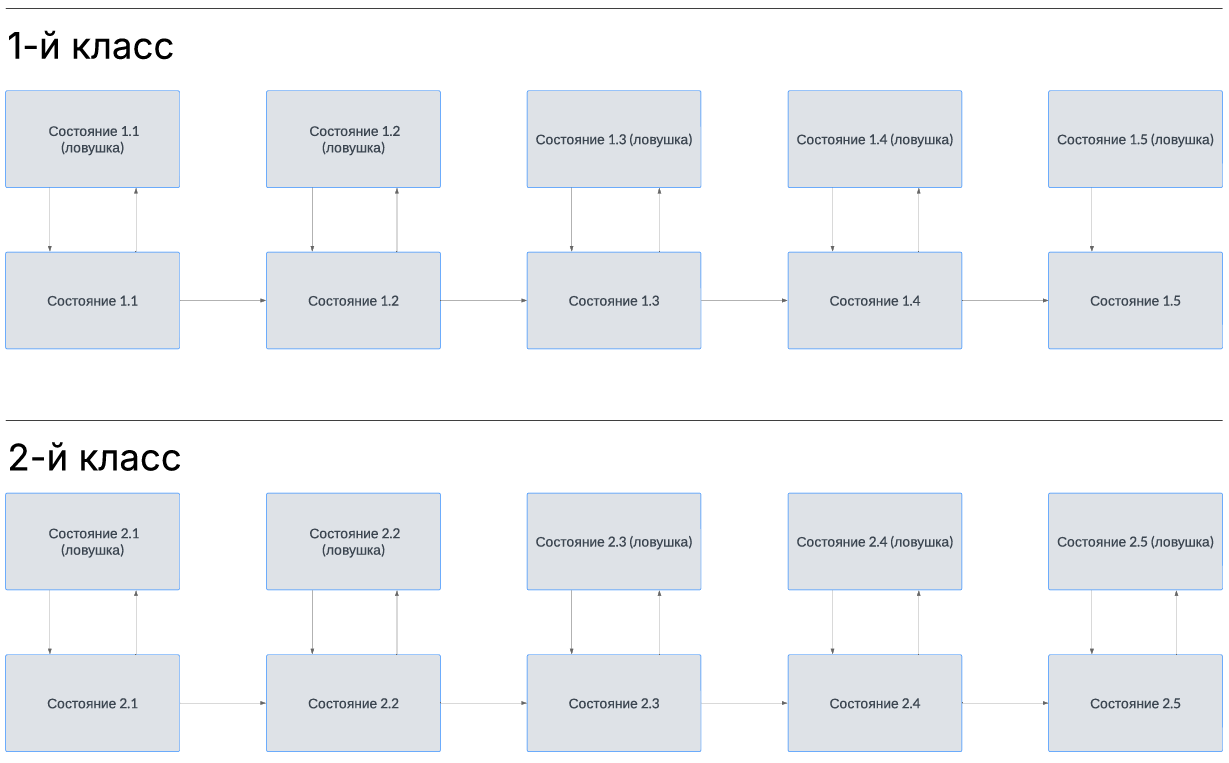
Рис. 3. Марковский процесс с пятью парами состояний и переходами между ними
Fig. 3. Markov process with five pairs of states and transitions between them
Для формирования адаптивной траектории обучения следует определить взаимосвязь тем начиная со второго класса с ранее изученными материалами, представленными в парах состояний младших классов. Это позволяет сформировать учебную траекторию для каждой темы пар состояний начиная с простейших заданий и понятий (рис. 4).
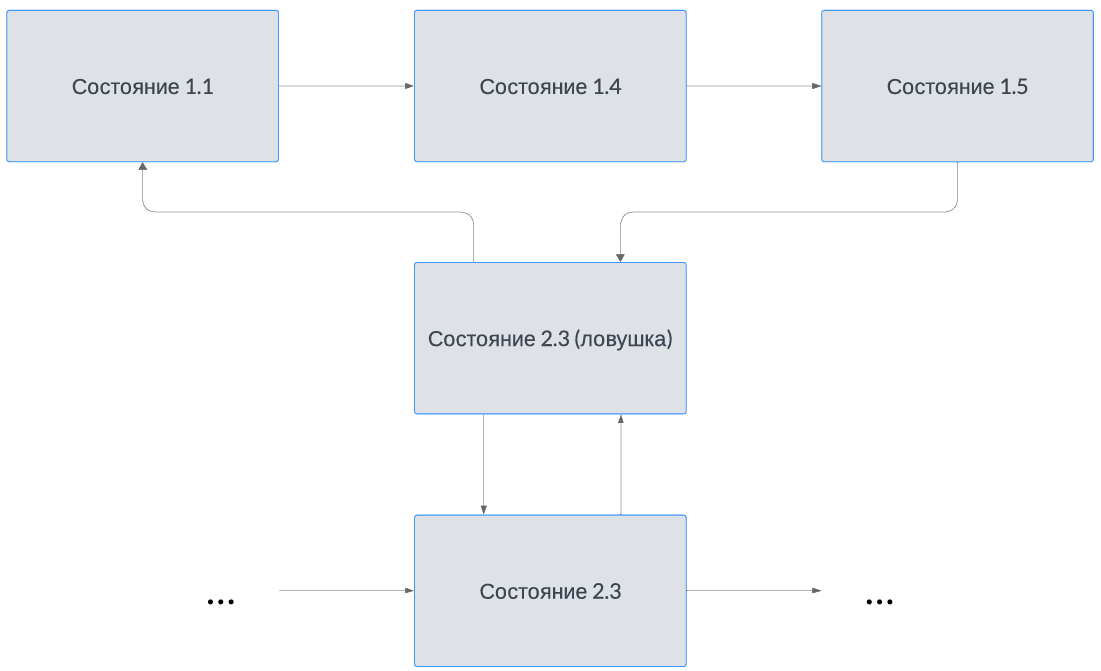
Рис. 4. Трехуровневая группировка состояний марковского процесса
Fig. 4. Three-level grouping of states of a Markov process
Обсуждение результатов
Обновление модели прототипа веб-приложения позволило реализовать адаптивную траекторию обучения для каждого пользователя. Теперь пользователю предоставляются состояния марковского процесса, которые наиболее соответствуют его уровню подготовки. Подобная реализация позволяет выявить пробелы в знаниях учеников и, по возможности на основе подсказок, закрыть самые маленькие из них, так как не всегда представляется возможность средствами системы за ограниченный период времени донести необходимую информацию до учащегося.
Подобная система призвана работать в паре с учителем для автоматизации процесса выявления пробелов в знаниях учеников. В рамках статьи приведены простые примеры распределения материалов по состояниям марковского процесса. Каждый пользователь системы может самостоятельно составить свою траекторию обучения для каждой из пары состояний в соответствии со своими потребностями.
В рамках системы каждый пользователь проходит свой путь по состояниям марковского процесса (рис. 5).
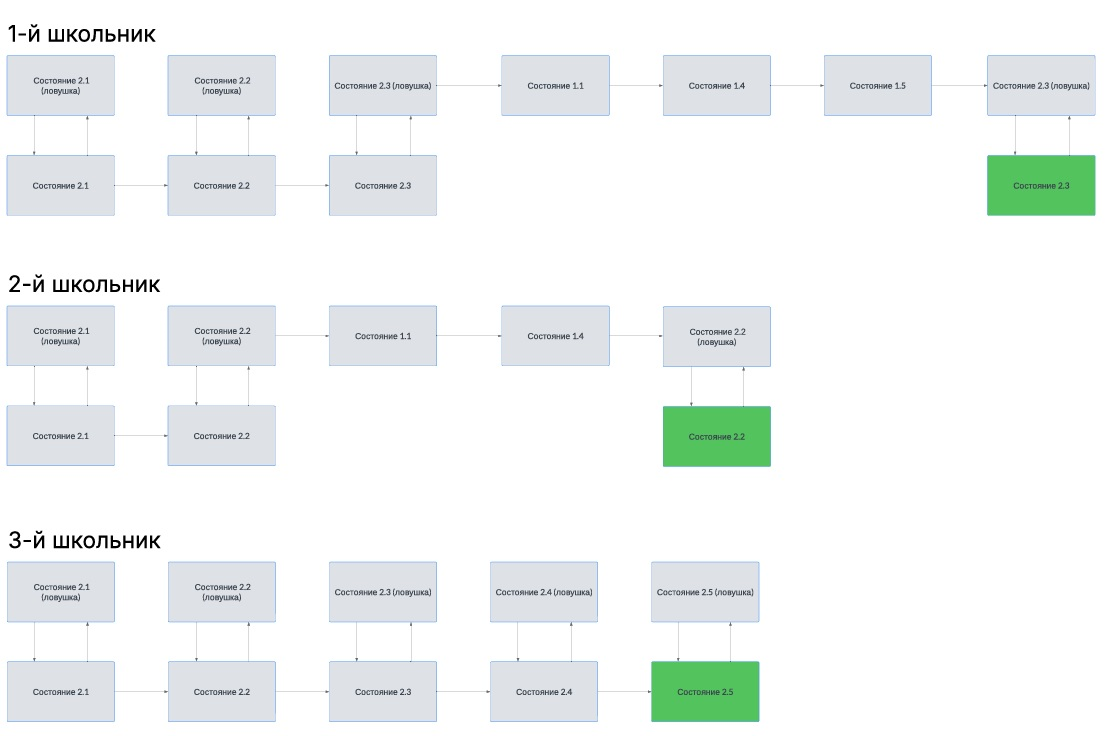
Рис. 5. Адаптивная траектория обучения в рамках системы
Fig. 5. Adaptive learning trajectory within the system
На рисунке выше представлена траектория обучения трех школьников в рамках разработанной системы. Зеленым выделены состояния выхода из марковского процесса по его завершению или истечению времени, выделенному на его выполнение. Первый школьник успешно прошел две пары состояний и испытал трудности с третьей. Ему были предоставлены дополнительные состояния марковского процесса для прохождения и выявления пробелов, которые мешали ему решить задачу из третьей пары состояний. После прохождение трех состояний он вернулся к решению задачи где он допустил ошибку. Решив её, он вернулся в обычное состояние где у него закончилось время. Следующий школьник верно решил первую пару состояний и столкнулся с проблемами во второй. Последний верно решил все пары состояний и ни разу не попал в дополнительные состояния. Таким образом траектория обучения для всех стала уникальной и наиболее соответствовала их подготовке.
Заключение
Внедрение цифровых систем в образование призвано улучшить процесс обучения за счет автоматизации рутинных задач учителя. Выявление пробелов в знаниях учащихся является одной из них. Не всегда представляется возможность детально понять на каком уровне обучения возникли трудности с освоением материала. Это приводит к невозможности решения более сложных задач, идущих дальше по программе. С помощью цифровых систем данный труд можно автоматизировать и предоставить учителю детальную информацию на каком этапе ученик испытывает трудности.
Дополнение марковского процесса новыми состояниями позволило реализовать адаптивную траекторию обучения для каждого обучающегося, предоставляя состояния с задачами, которые наиболее хорошо подходят к индивидуальному уровню подготовки.
Разработанный механизм также позволяет автоматизировать контроль педагога за успеваемостью учеников, используя систему в качестве помощника для выявления пробелов в знаниях при решении задач, основывающихся на ранее пройденных учебных материала.