Алгебраические кривые высших порядков в преподавании высшей математики. Методы построения алгебраических кривых

Е.Д. Куланин; М.Е. Степанов

doi:10.17759/mda.2025150408

Моделирование и анализ данных
2025. Том 15. № 4. С. 122–137
doi:10.17759/mda.2025150408
ISSN: 2219-3758 / 2311-9454 (online)

Алгебраические кривые высших порядков в преподавании высшей математики. Методы построения алгебраических кривых

Е.Д. Куланин, М.Е. Степанов

Резюме

Контекст и актуальность. В рабочих программах дисциплин «Геометрия и топология», «Математический анализ», «Математика» и других, входящих в образовательные программы специальностей по информационным технологиям, важное место занимает понятие алгебраической кривой. Освоение этого понятия требует от студентов способности к абстрактному мышлению и зачастую вызывают существенные затруднения. Цель. Повысить качество усвоения учебного материала по дисциплинам, связанным с понятием алгебраической кривой, используя при этом программные средства для визуализации различных алгебраических кривых и семейств алгебраических кривых. Ещё одной не менее важной целью является описание вопросов, которые могут стать темами курсовых и дипломных работ. Гипотеза. Использование программных средств для визуализации различных алгебраических кривых и семейств алгебраических кривых позволяет преподавателю максимально понятно подать материал, а студентам лучше усвоить материал и получить навыки решения задач на построение алгебраических кривых. Методы и материалы. В большинстве заданий в этой статье предлагается написать компьютерную программу, визуализирующую алгебраические кривые и их семейства. Результаты. Разработана система заданий, позволяющих студентам строить алгебраические кривые с помощью компьютерных программ. Выводы. Применение разработанной системы учебных заданий подтвердило важность использования специальных программных средств для усвоения материала по теории алгебраических кривых.

Общая информация

Ключевые слова: высшее образование, методика преподавания математики, аналитическая геометрия, визуальные образы, алгебраические кривые, методы построения, геометрические образы, геометрические преобразования

Рубрика издания: Методика преподавания

Тип материала: научная статья

DOI: https://doi.org/10.17759/mda.2025150408

Поступила в редакцию 17.10.2025

Поступила после рецензирования 27.10.2025

Принята к публикации 29.10.2025

Опубликована 28.12.2025

Для цитаты: Куланин, Е.Д., Степанов, М.Е. (2025). Алгебраические кривые высших порядков в преподавании высшей математики. Методы построения алгебраических кривых. Моделирование и анализ данных, 15(4), 122–137. https://doi.org/10.17759/mda.2025150408

Лицензия: CC BY-NC 4.0

Полный текст

Введение

Статья продолжает цикл методических разработок авторов (Куланин Е. Д., Степанов М. Е., Нуркаева И.М., 2020; Куланин Е. Д., Степанов М. Е., Нуркаева И.М., 2021; Куланин Е. Д., Степанов М. Е., 2024; Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А., Куланин Е.Д., 2013). Непосредственно она продолжает статью «Алгебраические кривые низших порядков в преподавании высшей математики» (Куланин, Степанов, 2025). В ней обсуждаются некоторые проблемы, связанные с путями повышения культуры математического мышления студентов-математиков. Главным объектом обсуждения являются алгебраические кривые степени выше двух. Авторы опираются на опыт работы на факультете информационных технологий МГППУ.

В статье (Куланин, Степанов, 2025) рассматривались алгебраические линии не выше второго порядка, а также их семейства. Там же описан метод построения алгебраических кривых на экране компьютера с помощью сканирования декартовой плоскости. Этот метод позволяет строить любые линии, описанные неявными уравнениями, в том числе трансцендентные. По этой причине многие задания, рассмотренные в данной статье, могут быть перенесены на более широкий круг математических тем.

В большинстве заданий в этой статье предлагается написать компьютерную программу, визуализирующую алгебраические кривые и их семейства. Авторы считают, что геометрические образы должны максимально интенсивно использоваться в обучении высшей математике (Куланин Е. Д., Нуркаева И. М., Степанов М. Е., 2020; Куланин Е. Д., Нгуен Ву Куанг, Степанов М. Е., 2019; Куланин Е. Д., Степанов М. Е., 2022 DOI: https://doi.rg/10.17759/mda.2022120407; Куланин Е. Д., Степанов М. Е.,2022 DOI: https://doi.org/10.17759/mda.2024140212).

Предоставление возможности студентам с помощью компьютера самостоятельно строить алгебраические кривые, является одной из важных целей данной статьи.

Ещё одной не менее важной целью является описание вопросов, которые могут стать темами курсовых и дипломных работ.

Построение образов алгебраических кривых на экране

Традиционные формы преподавания высшей математики используют чертежи, как обязательный методический приём. Экстремисты от математики с удивительной активностью пытались изгнать визуальные образы математических объектов из курсов не только высшей, но и школьной математики (Дьедонне Ж., 1972).

Однако по мнению авторов данной статьи использование различных образов является одним из важнейших способов развития математической интуиции студентов. В частности, построение на экране кривых и поверхностей даёт учащемуся возможность увидеть большое количество геометрических объектов, которые до появления компьютеров строились с большим трудом. Если же студент сам пишет подобную программу, он, кроме всего прочего, должен детально разобраться в математических аспектах описания соответствующего объекта.

Рассмотрим несколько примеров построения алгебраических кривых на экране компьютера. При этом хорошим путеводителем по замечательным кривым является книга (Савёлов А. А., 1960). Ориентируясь на изложенный в ней материал, рассмотрим одну из описанных там кривых.

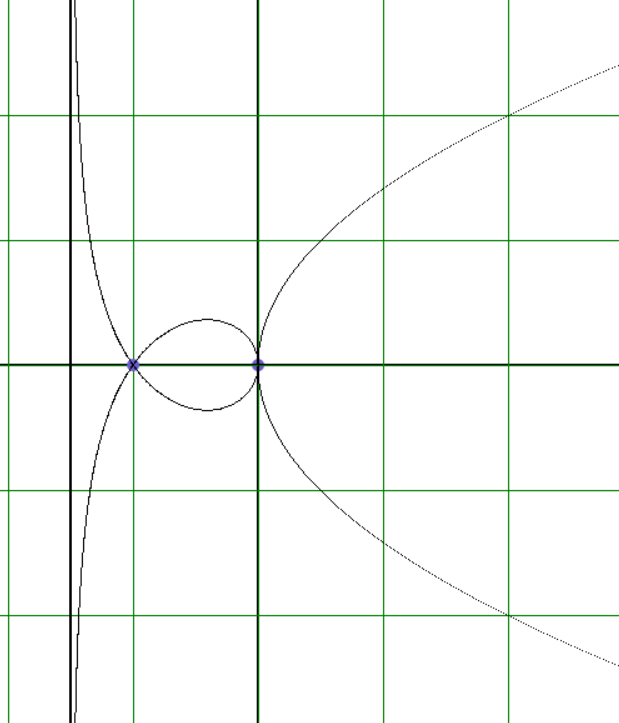
Будем строить трисектрису Маклорена, используя её геометрическое описание. Трисектриса Маклорена является подэрой параболы относительно такой точки её оси, которая удалена от директрисы на расстояние, равное расстоянию директрисы от фокуса (фокальное расстояние). Подэрой данной кривой относительно какой-либо точки плоскости называется новая кривая, представляющая собой геометрическое место оснований перпендикуляров, опущенных из этой точки на касательные к заданной кривой (Савёлов А. А., 1960).

Задание 1. Построить на экране параболу и семейство касательных к ней.

Решение. Уравнение параболы имеет вид

y^{2} = 2 px

, где р – фокальное расстояние параболы. Если менять в цикле ординату

y_{k}

, то

x_{k} = \frac{y_{k}^{2}}{2 p}

. Касательная, проходящая через точку (

x_{k}; y_{k}

по свойству касательных к параболе также проходит через точку (0;

\frac{y_{k}}{2}

). Из этого следует, что уравнение касательной имеет вид

y = k ∙ x + b

, где

k = \frac{y_{k}}{2 ∙ x_{k}} = \frac{y_{k} ∙ p}{2 p ∙ x_{k}} = \frac{p}{y_{k}}

b = \frac{y_{k}}{2}

Построенное программой изображение показано на рисунке 1.

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

'Фокальное расстояние параболы

p = 1

'Начало экранных координат

x0 = 300

y0 = 300

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

GraphicsWindow.DrawLine(0,y0,600,y0)

GraphicsWindow.DrawLine(x0,0,x0,600)

'Количество пикселов в единичном отрезке

ed = 100

'Сетка единичных квадратов

For x=-3 To 3 Step .01

For y=-3 To 3 Step 1

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

For x=-3 To 3 Step 1

For y=-3 To 3 Step .01

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"green")

EndFor

'Построение параболы

For y = 0 To 9 Step .01

x = y*y/(2*p)

xe=x0 + ed*x

ye=y0 - ed*y

GraphicsWindow.SetPixel(xe,ye,"")

ye=y0 + ed*y

GraphicsWindow.SetPixel(xe,ye,"")

EndFor

'Касательные к параболе

For yk = .5 To 9 Step .1

xk = yk*yk/(2*p)

xe=x0 + ed*xk

ye=y0 - ed*yk

k = yk/(2*xk)

b = yk/2

For t = - 3 To 3 Step .01

u = k*t + b

xe=x0 + ed*t

ye=y0 - ed*u

GraphicsWindow.SetPixel(xe,ye,"")

ye=y0 + ed*u

GraphicsWindow.SetPixel(xe,ye,"")

EndFor

Рис. 1. Парабола и семейство касательных к ней

Fig. 1. A parabola and a family of tangents to it

Задание 2. Построить трисектрису Маклорена как подэру параболы. Найти уравнение асимптоты к ней.

Решение. Поскольку уравнение касательной к параболе, выведенное в предыдущем задании, имеет вид

y = k ∙ x + b

, то можно получить уравнение ортогональной прямой, проходящей через точку (

- p; 0

. Пусть это уравнение имеет вид

y = k_{1} ∙ x + b_{1}

. Тогда

k_{1} = \frac{- 1}{k}

b_{1} = \frac{- p}{k}

. Точка пересечения этих прямых имеет координаты

x_{t} = \frac{- b - b_{1}}{k - k_{1}}

y = k_{1} ∙ x_{t} + b_{1}

Все коэффициенты двух прямых зависят от параметра

y_{k}

. Достаточно простые преобразования позволяют выразить зависимость от

y_{k}

x_{t} = \frac{3}{2} p ∙ \frac{y_{k}^{2}}{p^{2} - y_{k}^{2}}

. При

y_{k}

стремящемся к бесконечности

x_{t}

стремится к

\frac{- 3}{2} p

. Таким образом, уравнение асимптоты имеет вид

x = \frac{- 3}{2} p

В программе часть, посвящённую проведению касательных, следует заменить на новые строки. Результат работы программы показан на рисунке 2.

'Точка на плоскости

xe = x0 - p*ed

GraphicsWindow.FillEllipse(xe - 5, y0 - 5, 10, 10)

'Построение подэры

'Параметры касательной

For yk = .1 To 9 Step .01

xk = yk*yk/(2*p)

xe=x0 + ed*xk

ye=y0 - ed*yk

k = yk/(2*xk)

b = yk/2

'Основания перпендикуляров

k1 = -1/k

b1 = -p/k

xt = -(b - b1)/(k - k1)

yt = k*xt + b

xe=x0 + ed*xt

ye=y0 - ed*yt

GraphicsWindow.SetPixel(xe,ye,"")

ye=y0 + ed*yt

GraphicsWindow.SetPixel(xe,ye,"")

EndFor

'Асимптота

xe = x0 - p*ed*1.5

GraphicsWindow.DrawLine(xe, 0, xe, 600)

Рис. 2. Трисектриса Маклорена

Fig. 2. Maclaurin's Trisector

В статье (Куланин Е. Д., Степанов М. Е., 2025, с.210-251) показан метод построения кривых сканированием.

Задание 3. Методом сканирования построить кривую, называемую офиуридой по её уравнению

x (x^{2} + y^{2}) = y (cy - bx)

(Савёлов А. А., 1960).

Решение. Результат работы программы показан на рисунке 3.

GraphicsWindow.Width = 200

GraphicsWindow.Height = 600

x0 = 50

y0 = 300

ed = 10

b = 10

c = 5

GraphicsWindow.DrawLine(c*ed+x0,0,c*ed+x0,600)

For x = -5 To 15 Step .01

For y = -30 To 30 Step .01

z = x*(x*x + y*y) - y*(c*y - b*x)

If Math.Abs(z)<.3 Then

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe, ye, "blake")

EndIf

EndFor

GraphicsWindow.DrawLine(x0 + c*ed, 0, x0 + c*ed, 600)

Задание 4. Офиурида является подэрой параболы относительно какой-либо точки, лежащей на касательной к вершине этой параболы. Построить офиуриду, отправляясь от этого факта.

Меняя формулу, описывающую кривую, можно с помощью последней программы ознакомиться с формой многочисленных линий. Однако для более удобного изучения кривых следует написать интерактивную программу, позволяющую пользователю выбирать очередную кривую из определённого набора. Для более чёткой фиксации важности этого типа программ сформулируем требование их разработки в виде задания.

Задание 5. Написать программу, позволяющую в интерактивном режиме просматривать некоторый набор алгебраических кривых.

О возможных решениях. Предлагаемое задание можно выполнить различными способами в зависимости от конкретных требований к программе. Это может относится к списку кривых, которые можно просматривать; к подробности описания каждой из кривых, например, по типу заданий 1 и 2. Тем более, самыми различными могут быть интерфейсы программ. Учитывая это, можно предлагать разработку подобных программ как тему курсовой и даже дипломной работы.

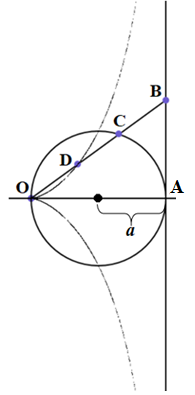
Приведём пример конкретной темы, которая может стать примером дипломной работы. С этой целью мы рассмотрим циссоиду Диоклеса (рис. 4) и циссоидальные преобразования (Савёлов А. А., 1960).

Циссоиду Диоклеса можно определить двумя способами: с помощью уравнения

y^{2} ∙ (2 a - x) - x^{3}

и геометрически. Геометрическое определение таково. Построим на декартовой плоскости с началом координат в точка О окружность радиуса а с центром в точке

(a; 0)

и касательную к ней в точке

(2 a; 0)

. Выберем на касательной произвольную точку В и проведём отрезок ОВ. Пусть точка С является точкой пересечения окружности и отрезка ОВ. Построим на том же отрезке ОВ точку D, такую что ОВ = ОD. Эта точка лежит на циссоиде Диоклеса. Таким образом, эту кривую образует множество всех подобных точек.

Рис 4 — Рис. 4. Циссоида Диоклеса

Fig. 4. Cyssoid of Diocles

Задание 6. Написать программу, которая строит циссоиду по уравнению с помощью сканирования. Кроме того, на экране следует отобразить окружность, прямую АВ, произвольно заданный отрезок ОВ (например, с помощью выбора угла наклона) и точки С и D. В итоге будет построен рисунок 4. Факт прохождения циссоиды через точку D должен подтвердить согласованность двух определений циссоиды Диоклеса.

Решение. Приведём соответствующую программу.

Pi = Math.Pi

GraphicsWindow.Width = 300

GraphicsWindow.Height = 600

x0 = 50

y0 = 300

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

ed = 10

a = 10

u0 = pi/5

h = 2*a*Math.Tan(u0)

x1 = x0 + 2*a*ed

y1 = y0 - h*ed

GraphicsWindow.FillEllipse(x0 - 5, y0 - 5,10,10)

GraphicsWindow.DrawLine(x1,0,x1,600)

GraphicsWindow.DrawLine(0,y0,300,y0)

GraphicsWindow.DrawEllipse(x0, y0 - a*ed, 2*a*ed, 2*a*ed)

GraphicsWindow.DrawLine(x0,y0,x1,y1)

GraphicsWindow.FillEllipse(x1 - 5,y1 - 5,10,10)

d1 = Math.SquareRoot(4*a*a + h*h)

d2 = 2*a* Math.Cos(u0)

lm = d2/d1

x2 = x0 + lm*(x1 - x0)

y2 = y0 + lm*(y1 - y0)

GraphicsWindow.FillEllipse(x2 - 5,y2 - 5,10,10)

lm = 1 - lm

x3 = x0 + lm*(x1 - x0)

y3 = y0 + lm*(y1 - y0)

GraphicsWindow.FillEllipse(x3 - 5,y3 - 5,10,10)

For x = 0 To 2*a*ed Step .005

For y = -30 To 30 Step .005

z = x*x*x - y*y*(2*a - x)

xe = x0 + x*ed

ye = y0 - y*ed

If Math.Abs(z)<.08 Then

GraphicsWindow.SetPixel(xe, ye, "blake")

EndIf

EndFor

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

Задание 7. Написать программу, которая строит циссоиду Диоклеса, исходя из её геометрического определения.

Задание 8. Циссоида является множеством точек, симметричных вершине параболы относительно её касательных. Написать программу, которая строит циссоиду на основе этого факта.

Важным свойством циссоиды является то обстоятельство, что её можно использовать для решения делосской задачи. Дело в том, что на острове Делос разразилась эпидемия чумы. Дельфийский оракул оракул сообщил, что эпидемия закончится если в два раза увеличить объём кубического жертвенника. Для этого нужно построить куб со стороной

\sqrt[3]{2}

. С помощью циркуля и линейки сделать это невозможно. Именно по этой причине нужно задействовать циссоиду (Савёлов А. А., 1960; Прасолов В. В., 1997).

Задание 9. На основе изложенных фактов написать демонстрационную или обучающую программу, посвящённую циссоиде.

Перейдём к рассмотрению циссоидальных преобразований. Циссоида Диоклеса строится с помощью использования окружности и прямой. Если заменить их другими линиями, то получится новая кривая. На этом соображении даётся определение циссоидальных преобразований.

Если в полярных координатах заданы две кривые

ρ_{1} = f_{1} (φ)

ρ_{2} = f_{2}

), то циссоидой этих кривых называется кривая, задаваемая уравнением

F (φ) = f_{1} (φ) -

f_{2}

Задание 10. Доказать, что циссоида Диоклеса подпадает под это определение.

Естественно, что при таком определении циссоидальных преобразований можно построить сколь угодно много новых кривых. Ограничимся только одним примером.

Задание 11. Показать, что уравнение

y^{2} = 2 px + q x^{2}

при различных значениях параметров p и q описывает эллипсы, гиперболы и параболы.

Решение. При q = 0 уравнение описывает параболу. При q отличном от нуля следует выделить полный квадрат в правой части уравнения. В зависимости от знака q будет получено уравнение эллипса или параболы. Продемонстрировать этот факт можно также с помощью следующей программы

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

'Параметры исходной кривой

p = 3

q = -4

'Начало экранных координат

x0 = 300

y0 = 300

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

GraphicsWindow.DrawLine(0,y0,600,y0)

GraphicsWindow.DrawLine(x0,0,x0,600)

'Количество пикселов в единичном отрезке

ed = 100

'Сканирование декартовой плоскости

For x = -3 To 3 Step .01

For y = -3 To 3 Step .01

'Вычисление значений функции z = F(x, y)

z = y*y - 2*p*x - q*x*x

'Переход к экранной системе координат

xe = x0 + x*ed

ye = y0 - y*ed

If Math.Abs(z)<.01 Then

GraphicsWindow.SetPixel(xe, ye, "blake")

EndIf

EndFor

Задание 12. Возьмём в качестве образующих для циссоидальных преобразований линии

y^{2} = 2 px + q x^{2}

x = k

. Перейти к полярным координатам. Написать программу построения соответствующей циссоиды.

Решение. Переход к полярным координатам производится по формулам

x = ρ ∙ \cos φ

y = ρ ∙ \sin φ

. Без труда для первой образующей получаем формулу

ρ_{1} = \frac{2 p ∙ \cos φ}{\sin^{2} φ - {q ∙ \cos}^{2} φ}

, а для второй – формулу

ρ_{2} = \frac{k}{\cos φ}

. Программа будет строить и образующие, и циссоиду, в которую они преобразуются. Результат работы программы показан на рисунках 5 – 7 при разных параметрах p, q и k. При p = 4, q =

-

3 и k = 3 на рисунке 5 изображена циссоида эллипса; при p = 1, q = 1 и k = 1 на рисунке 6 изображена циссоида гиперболы; p = 1, q = 0 и k = 1 на рисунке 7 изображена циссоида параболы.

pi = Math.Pi

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

x0 = 300

y0 = 300

ed = 30

p = 4

q = -3

k = 3

For u = 0 To 2*pi Step pi/10000

zn1 = Math.Sin(u)*Math.Sin(u) - q*Math.Cos(u)*Math.Cos(u)

zn2 = Math.Cos(u)

If Math.Abs(zn1) > .001 And Math.Abs(zn2) > .001 Then

r1 = 2*p*Math.Cos(u)/zn1

r2 = k/zn2

r = r1 - r2

x1 = r1* Math.Cos(u)

y1 = r1 *Math.Sin(u)

xe = x0 + x1*ed

ye = y0 - y1*ed

GraphicsWindow.SetPixel(xe,ye,"")

x2 = r2* Math.Cos(u)

y2 = r2 *Math.Sin(u)

xe = x0 + x2*ed

ye = y0 - y2*ed

GraphicsWindow.SetPixel(xe,ye,"")

x = r* Math.Cos(u)

y = r* Math.Sin(u)

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.FillEllipse(xe-1,ye-1,2,2)

EndIf

EndFor

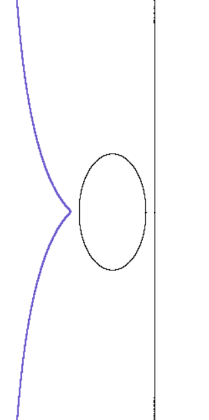
Рис. 5. Циссоида эллипса

Fig. 5. The cissoid of the ellipse

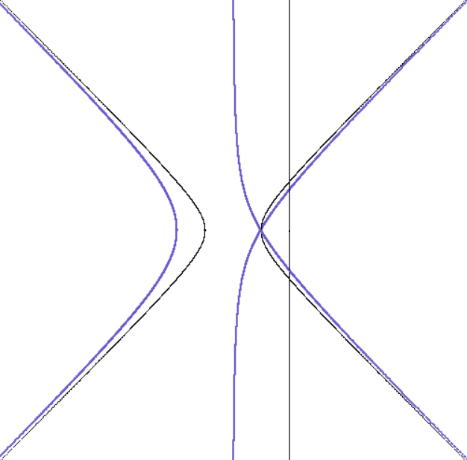
Рис. 6. Циссоида гиперболы

Fig. 6. The cissoid of hyperbola

Рис. 7. Циссоида параболы
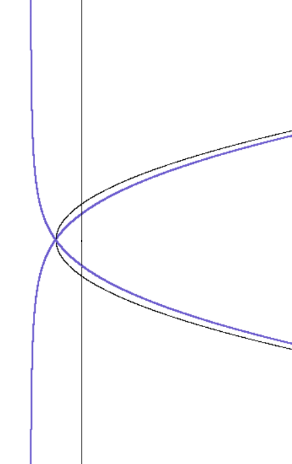
Fig. 7. The cissoid of the parabola

Заключение

В данной статье рассматриваются вопросы, связанные с углублённым изучением линий выше второго порядка. Особое внимание уделяется методам построения алгебраических кривых.

Обсуждение соответствующих вопросов может помочь молодым преподавателям при изучении различных разделов высшей математики. Кроме того, некоторые рассмотренные темы могут быть предложены в качестве тем курсовых и дипломных работ.

Литература

Дьедонне Ж. Линейная алгебра и элементарная геометрия. М., Наука, 1972.
Dieudonné, J. Linear Algebra and Elementary Geometry. Moscow, Nauka, 1972.
Куланин Е. Д., Нгуен Ву Куанг., Степанов М. Е. Осязаемая предметность с компьютерной поддержкой. // Моделирование и анализ данных. 2019. Том № 4. С. 145–156. DOI: https://doi: 10.17759/mda.2019090412
Kulanin E. D., Nguyen Vu Quang, and Stepanov M. E. Tangible Subjectivity with Computer Support. // Modeling and Data Analysis. 2019. Vol. 09. No. 4. Pp. 145–156. DOI: https://doi: 10.17759/mda.2019090412
Куланин Е. Д., Степанов М. Е. Использование образов в преподавании высшей математики. // Моделированиеианализданных. 2024. Том № 2. C. 192–225. DOI: https://doi. org/10.17759/mda.2024140212
Kulanin E. D., Stepanov M. E. Using Images in Teaching Higher Mathematics. // Modeling and Data Analysis. 2024. Vol. 14. No. 2. Pp. 192–225. DOI: https://doi.org/10.17759/mda.2024140212
Куланин Е. Д., Степанов М. Е. О визуализации решений некоторых экстремальных задач. // Моделирование и анализ данных. 2022. Том № 4. C. 94–104. DOI: https://doi. org/10.17759/mda.2022120407
Kulanin E. D., Stepanov M. E. On the visualization of solutions to some extremal problems. // Modeling and Data Analysis. 2022. Vol. 12. No. 4. Pp. 94–104. DOI: https://doi.org/10.17759/mda.2022120407
Куланин Е. Д., Степанов М. Е., Нуркаева И. М. Роль образного мышления в научном мышлении. // Моделирование и анализ данных. Том 10. № 2. C. 110–128. DOI: https://doi:10.17759/mda.2020100209
Kulanin E. D., Stepanov M. E., Nurkaeva I. M. The Role of Imagination in Scientific Thinking. // Modeling and Data Analysis. 2020. Vol. 10. No. 2. Pp. 110–128. DOI: https://doi:10.17759/mda.2020100209
Куланин Е.Д., Степанов М. Е. Всестороннее рассмотрение математических понятий как методический прием. // Моделированиеианализданных. 2022. Том № 4. C. 67–84. DOI:https://doi.org/10.17759/mda.2022120405
Kulanin E.D., Stepanov M. E. Comprehensive Review of Mathematical Concepts as a Methodological Approach. // Modeling and Data Analysis. 2022.Vol. 12. No. 4. Pp. 67–84. DOI: https://doi.org/10.17759/mda.2022120405
Куланин Е.Д., Степанов М. Е. Вычислительный эксперимент в преподавании высшей математики на примере теории чисел. // Моделирование и анализ данных. 2024. Том 14. № 1. C. 170–195. DOI: https://doi.org/10.17759/mda.2024140111 12.
Kulanin E.D., Stepanov M. E. Computational Experiment in Teaching Higher Mathematics on the Example of Number Theory. // Modeling and Data Analysis. Vol. 14. No. 1. Pp. 170–195. DOI: https://doi.org/10.17759/mda.2024140111 12.
Куланин Е.Д., Степанов М. Е. Вычислительный эксперимент в преподавании высшей математики. Комбинаторика и её приложения. // Моделирование и анализ данных. Том 14. № 3. C. 174–202. DOI: https://doi.org/10.17759/mda.2024140310
Kulanin E.D., Stepanov M. E. Computational Experiment in Teaching Higher Mathematics. Combinatorics and Its Applications. // Modeling and Data Analysis. 2024. Vol. 14. No. 3. Pp. 174–202. DOI: https://doi.org/10.17759/mda.2024140310
Куланин Е.Д., Степанов М. Е. Из опыта работы в режиме дистанционного обучения // Моделирование и анализ данных. Том 12. № 3. C. 58–70. DOI: https://doi. org/10.17759/mda.2022120305
Kulanin E.D., Stepanov M. E. From the experience of working in remote mode education // Data modeling and analysis. 2022. Volume 12. No. 3. pp. 58-70. DOI: https:// doi. org/10.17759/mda.2022120305
Куланин Е.Д., Степанов М. Е. Использование образов в преподавании высшей математики. // Моделирование и анализ данных. Том 14. № 2. C. 192–225. DOI: https://doi. org/10.17759/mda.2024140212
Kulanin E.D., Stepanov M. E. Using Images in Teaching Higher Mathematics. // Modeling and Data Analysis. 2024. Vol. 14. No. 2. Pp. 192–225. DOI: https://doi.org/10.17759/mda.2024140212
Куланин Е.Д., Степанов М. Е., Нуркаева И.М. О различных подходах к решению экстремальных задач. // Моделирование и анализ данных. 2021. Том № 1. C. 40–60. DOI: https://doi.org/10.17759/mda.2021110104
Kulanin E.D., Stepanov M. E., Nurkaeva I.M. On Different Approaches to Solving Extreme Problems. // Modeling and Data Analysis. 2021. Vol. 11. No. 1. Pp. 40–60. DOI: https://doi.org/10.17759/mda.2021110104
Куланин Е.Д., Степанов М.Е. Алгебраические кривые низших порядков в преподавании высшей математики // Моделирование и анализ данных. Том 15. № 1. C. 210–251. DOI: https://doi.org/10.17759/mda.2025150111
Kulanin E.D., Stepanov M.E. Algebraic Curves of Lower Orders in Teaching Higher Mathematics // Modeling and Data Analysis. 2025. Vol. 15. No. 1. Pp. 210–251. DOI: https://doi.org/10.17759/mda.2025150111
Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А., Куланин Е.Д. Сборник задач по высшей математике с контрольными работами. Москва, 2013. Том 2 (8-е издание).
Lungu K.N., Norin V.P., Pismenny D.T., Shevchenko Yu.A., Kulanin E.D. Collection of Problems in Higher Mathematics with Control Works. Moscow, 2013. Volume 2 (8th edition).
Прасолов В. В. Геометрические задачи древнего мира. М., ФАЗИС, 1997.
Prasolov, V. V. Geometric Problems of the Ancient World. Moscow, FAZIS, 1997.
Савёлов А. А. Плоские кривые. Систематика, свойства, применения. (Справочное руководство). М., Гос. изд. физ.-мат. литературы. 1960.
Savelov A. A. Flat curves. Taxonomy, properties, applications. (Reference manual). M., State Publishing House of Physics and Mathematics. literatures. 1960.
Степанов М. Е., Куланин Е.Д. Множества точек, находящихся на рациональных расстояниях друг от друга. // Моделирование и анализ данных. Том 15. № 1. C. 210-251. DOI: https://doi.org/10.17759/mda.2025150111
Stepanov M. E., Kulanin E.D. Sets of points located at rational distances from each other. // Modeling and Data Analysis. 2025. Vol. 15. No. 1. C. 210-251. DOI: https://doi.org/10.17759/mda.2025150111

Информация об авторах

Евгений Дмитриевич Куланин, кандидат физико-математических наук, профессор, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), Москва, Российская Федерация, ORCID: https://orcid.org/0000-0001-6093-7012, e-mail: lucas03@mail.ru

Михаил Евграфович Степанов, кандидат педагогических наук, доцент кафедры прикладной математики факультета информационных технологий, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), Москва, Российская Федерация, ORCID: https://orcid.org/0000-0003-4803-8211, e-mail: mestepanov@yandex.ru

Вклад авторов

Куланин Е.Д. — идеи исследования, написание и оформление рукописи, разработка методики, планирование исследования, визуализация результатов исследования.

Степанов М.Е. — идеи исследования, написание и оформление рукописи; разработка описанного ПО, планирование исследования, визуализация результатов исследования.

Все авторы приняли участие в обсуждении результатов и согласовали окончательный текст рукописи.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Метрики

Просмотров web

За все время: 36
В прошлом месяце: 15
В текущем месяце: 21

Скачиваний PDF

За все время: 8
В прошлом месяце: 3
В текущем месяце: 5

Всего

За все время: 44
В прошлом месяце: 18
В текущем месяце: 26

PlumX

Метрики публикации