Трансформеры в задачах прогнозирования временных рядов: теоретические основы архитектур

В.А. Орищенко

doi:10.17759/mda.2025150402

Введение

Прогнозирование временных рядов часто служит основой для принятия решений в различных предметных областях. Высокая адаптивность моделей способствует высокой точности прогнозирования, что несет высокую пользу в различных направлениях, включая принятие решений в бизнес-процессах, стабильную работоспособность сложных технических систем. Классические методы, например, ARIMA (авторегрессионное интегрированное скользящее среднее) (Бокс, Дженкинс, Рейнсел, 1974), требуют строгих предположений о стационарности данных и линейности зависимостей, что редко выполняется в условиях реального мира. Рекуррентные нейронные сети (RNN), в частности LSTM (долгая краткосрочная память) (Hochreiter, 1997), позволяют преодолеть эти ограничения, моделируя нелинейные паттерны в наблюдаемых данных. Однако их рекуррентная архитектура приводит к экспоненциальному затуханию градиентов при обработке последовательностей длиной более ~1000 шагов (Pascanu, 2013), а последовательные расчёты создает трудности для параллельных вычислений.

Появление трансформеров (Vaswani, 2017), частного случая глубоких нейронных сетей, в 2017 году стало прорывом в обработке последовательностей. Его механизм multi-head attention эффективно выявляет долгосрочные зависимости, а отсутствие рекуррентных связей позволяет обрабатывать данные параллельно. Эти преимущества делают трансформеры эффективным инструментом для прогнозирования временных рядов. Однако, имеется ряд ограничений:

1.Высокая вычислительная сложность $O$ ) для последовательностей длины $L$ делает обучение неэффективным при $L > 10^{4}$ ;
2.Отсутствие встроенных механизмов для работы с нестационарностью, характерной для данных с высокой степенью динамики характеристик;
3.Игнорирование структурных характеристик временных рядов (тренд, сезонность), которые легко моделируются классическими статистическими методами.

Современные исследования предлагают адаптировать трансформеры под специфику временных рядов. Например, Informer (Zhou, 2021) использует разреженное внимание для снижения сложности, Autoformer (Wu, 2021) интегрирует декомпозицию тренд-сезонность, а FEDformer (Liu, 2022) применяет частотные преобразования для подавления шума. Несмотря на эмпирически доказанную эффективность этих моделей, имеется ограниченное количество научных материалов, которые описывают механизм работы указанных выше алгоритмов с временными рядами.

В рамках данной статьи детально будет рассмотрен подход в прогнозировании временных рядов с использованием различных вариаций трансформеров.

Эволюция методов прогнозирования

Классические методы моделирования временных рядов опираются на гипотезу о том, что будущее состояние системы зависит от ее прошлого. Модель

ARIMA (p, d, q)

формализует это через линейную комбинацию авторегрессионных

(p)

и скользящих средних

(q)

членов с предварительным дифференцированием

(d порядка)

для достижения стационарности:

\begin{matrix} \nabla^{d} y_{t} = c + \sum_{i = 1}^{p} (ϕ_{i} y_{t - i}) + \sum_{j = 1}^{q} (θ j ε_{t - j}) + ε_{t}, (1) \end{matrix}

где

\nabla^{d} =

— оператор дифференцирования (

B

— оператор запаздывания),

ε_{t} N (0, σ^{2})

. Несмотря на интерпретируемость, ARIMA не учитывает экзогенные переменные и нелинейные зависимости.

Рекуррентные нейросетевые подходы, например, LSTM (Hochreiter, 1997), заменяют линейные коэффициенты адаптивными весами. Обновление скрытого состояния

h_{t}

в LSTM включает три типа «ворот» (input, forget, output):

\begin{matrix} {\begin{matrix} f_{t} = σ (W_{f} ∙ [h_{t - 1}, x_{t}] + b_{f}), \\ i_{t} = σ (W_{i} ∙ [h_{t - 1}, x_{t}] + b_{i}), \\ {\tilde{C}}_{t} = \tanh (W_{c} ∙ [h_{t - 1}, x_{t}] + b_{C}), \\ C_{t} = f_{t} ⨀ C_{t - 1} + i_{t} ⨀ {\tilde{C}}_{t}, \\ h_{t} = O_{t} \tanh ⨀ (C_{t}), \\ O_{t} = σ (W_{o} ∙ [h_{t - 1}, x_{t}] + b_{o}), \end{matrix} \\ (2) \end{matrix}

где

σ

— сигмоидная функция,

⨀

— поэлементное умножение. Хотя LSTM эффективно моделирует локальные паттерны, его рекуррентная структура ограничивает параллельные вычисления, а градиенты затухают при

L > 500

(Pascanu, 2013).

Трансформеры для временных рядов

Функция softmax является ключевым компонентом механизма внимания и определяется следующим образом. Пусть $z = (z_{1}, z_{2}, \dots, z_{n}) \in R^{n}$ – вектор входных значений. Функция softmax преобразует этот вектор в распределение вероятностей:

\begin{matrix} softmax (z_{i}) = \frac{e^{z_{i}}}{\sum_{j = 1}^{n} e^{z_{j}}}, i = 1, 2, \dots, n, \\ (3) \end{matrix}

где

\sum_{j = 1}^{n} softmax (z_{i}) = 1

и

softmax (z_{i}) > 0

для всех

i

. Эта функция обеспечивает нормализацию весов внимания и позволяет интерпретировать их как вероятности (Vaswani, 2017).

Исходная архитектура трансформера состоит из энкодера и декодера, каждый из которых содержит слои self-attention и feed-forward сетей. Self-attention вычисляет взвешенную сумму значений

V

с весами, зависящими от запросов

Q

и ключей

K

:

\begin{matrix} A ttention (Q, K, V) = softmax (\frac{Q K^{T}}{\sqrt{d_{K}}} + M) V, \\ (4) \end{matrix}

где

M

— маска, обеспечивающая причинность (для

t^{'} > t

значение

M_{t, t} = - \infty .

Сложность составляет

O (L^{2} d_{k})

, что неприемлемо для длинных временных рядов (в таком случае необходимо оптимизировать вычисления, используя мощные графические ускорители – GPU).

Источник: данная формула впервые была представлена в работе Vaswani et al. и стала основой для всех последующих архитектур трансформеров. Оригинальное определение приведено в уравнении (1) статьи (Vaswani, 2017).

Для адаптации трансформеров к временным рядам предложены следующие стратегии:

Разреженное внимание (Informer): ProbSparse-механизм выбирает $O (\log L)$ ключей для каждого запроса, снижая сложность до $O (L \log L)$ (Zhou, 2021).
Декомпозиция компонент (Autoformer): разделяет ряд на тренд и сезонность через скользящее среднее (Wu, 2021):

\begin{matrix} {T rend}_{t} = \frac{1}{2 k + 1} \sum_{τ = t - k}^{t + k} t_{τ} . \\ (5) \end{matrix}

Частотный анализ (FEDformer): применяет преобразование Фурье к $Q, K, V$ , выделяя доминирующие частоты (Liu, 2022)

Эти подходы требуют теоретического обоснования, особенно в контексте устойчивости к шуму и способности аппроксимировать нестационарные процессы.

Математические основы и архитектурные модификации

Формализация задачи прогнозирования временных рядов

Рассмотрим многомерный временной ряд

Y = {y_{1}, \dots, y_{t}} \in R^{t \times d}

, где

d

— количество признаков. Задача прогнозирования на

H

шагов вперёд формулируется как поиск отображения

f_{θ} : R^{L \times d} \to R^{H \times d}

, минимизирующего ожидаемую ошибку:

\begin{matrix} θ^{} = \arg \min_{θ} Ε_{Y D} [L (f_{0} (Y_{t - L : t}), Y_{t + 1 : t + H})], \\ (6) \end{matrix}

где

L

— функция потерь (например, средний квадрат отклонения),

D

— распределение данных.

Позиционное кодирование для временных рядов

Поскольку трансформер изначально не учитывает порядок последовательности, для прогнозирования временных рядов предложены улучшенные методы позиционного кодирования:

Временные эмбеддинги: для временной метки $t$ вектор кодируется как $P E (t) = [\sin (ω_{1} t), \cos (ω_{1} t), \dots, \sin (ω_{d} t), \cos (ω_{d} t)]$ , где частоты $ω_{i}$ выбираются из логарифмического диапазона для охвата разных периодов.
Скользящие окна с адаптивным масштабированием: для нестационарных рядов вводится нормировка $x_{t}^{'} = \frac{x_{t} - μ_{t - k : t}}{σ_{t - k : t}}$ , где $μ, σ$ — локальные среднее и стандартное отклонение.

Sparse Attention

Informer заменяет полное внимание на ProbSparse, основанное на теореме о разреженном приближении (Zhou, 2021):

Теорема 1 (о разреженном приближении). Пусть

Q, K \in R^{L \times d_{k}}

, тогда для любого

ε > 0

существует матрица

\tilde{A} \in R^{L \times L}

с

O (og \frac{L}{ε^{2}})

ненулевыми элементами, такая что

{‖ A - \tilde{A} ‖}_{F} \leq ε {‖ A ‖}_{F}

, где

A = softmax (\frac{Q K^{T}}{\sqrt{d_{k}}})

.

Источник: данная теорема является адаптацией результатов из работы, где Zhou et al. доказали существование эффективного разреженного приближения для матриц внимания с использованием ProbSparse-механизма (Zhou, 2021).

Практически это реализуется выбором

u

ключей с максимальной информативностью:

\begin{matrix} u = \arg \max_{u} \sum_{q \in Q} \log (\sum_{k \in K_{u}} e^{\frac{qk}{\sqrt{d_{k}}}}), \\ (7) \end{matrix}

где

K_{u}

— подмножество ключей.

Декомпозиция тренда и сезонности в Autoformer

В работах по анализу временных рядов тренд и сезонность часто разделяются через скользящее среднее. тогда сезонная компонента определяется как

{Seasonal}_{t} = y_{t} - {Trend}_{t}

. Такой подход минимизирует дисперсию остатков и обеспечивает интерпретируемость компонент (Бокс, 1974).

Теоретический анализ преимуществ и ограничений

Вычислительная сложность

Сравнение сложности методов (Табл. 1) показывает, что Informer и FEDformer оптимальны для длинных последовательностей. Однако их эффективность зависит от степени разреженности данных. Для рядов с высокой корреляцией

преимущества sparse-внимания снижаются.

Таблица 1 / Table 1

Теоретическая сложность методов (обучение)

Theoretical complexity of methods (training)

Метод	Сложность	Память	Условия применения
ARIMA	$O (L)$	$O (1)$	Стационарность
LSTM	$O (L d^{2})$	$O (Ld)$	$L < 500$
Transformer	$O (L^{2} d)$	$O (L^{2})$	$L < 10^{3}$
Informer	$O (L \log LD)$	$O (L logL)$	Низкая корреляция на больших $H$
Autoformer	$O (L \log LD + NL)$	$O (L logL)$	Устойчивая авторегрессия

Трансформер обеспечивает параллельную обработку последовательностей, снижая количество последовательных операций с

O (n)

для RNN до

O (1)

при сохранении возможности моделировать сложные зависимости (Vaswani, 2017).

Экспериментальный анализ в теоретическом контексте

Для верификации теоретических положений, изложенных в разделах 3–4, проведен сравнительный анализ эффективности различных архитектур на датасете потребления электроэнергии Individual household electric power consumption (количество строк – около 1 миллиона). Эксперименты проводились на графическом программном ускорителе – RTX 5070 – для оптимизации вычислений. Данные содержат измерения активной мощности с интервалом 1 минуту за период с 2006 по 2010 гг. В качестве целевой переменной использовалась активная мощность, а в качестве метрик — RMSE и MAE. Длина входной последовательности

L = 96

(96 минут), горизонт прогноза

H = 24

(24 минуты). Обучающая и тестовая выборки содержали 70% и 30% данных соответственно. Для сравнения были протестированы следующие модели:

1.LSTM — классическая рекуррентная сеть;
2.Трансформер — базовая архитектура с механизмом внимания;
3.Autoformer — адаптация трансформера с декомпозицией тренд-сезонность;
4.FEDformer — версия с частотным анализом.

Результаты эксперимента

Результаты прогнозирования представлены в табл. 2 и на рис. 1. Базовый трансформер продемонстрировал наилучшие показатели: RMSE = 0.5874, MAE = 0.3188. Это на 8.7% лучше LSTM и на 0.2% превосходит Autoformer. FEDformer показал средние результаты (RMSE = 0.6091), что, вероятно, связано с упрощенной реализацией частотного анализа в эксперименте.

Таблица 2 / Table 2

Сравнение метрик моделей на тестовой выборке

Comparison of model metrics on a test dataset.

Model	RMSE	MAE	Correlation
LSTM	0.6387	0.3769	0.8029
Transformer	0.5874	0.3188	0.8040
Autoformer	0.5880	0.3162	0.8039
FEDFormer	0.6091	0.330	0.7875

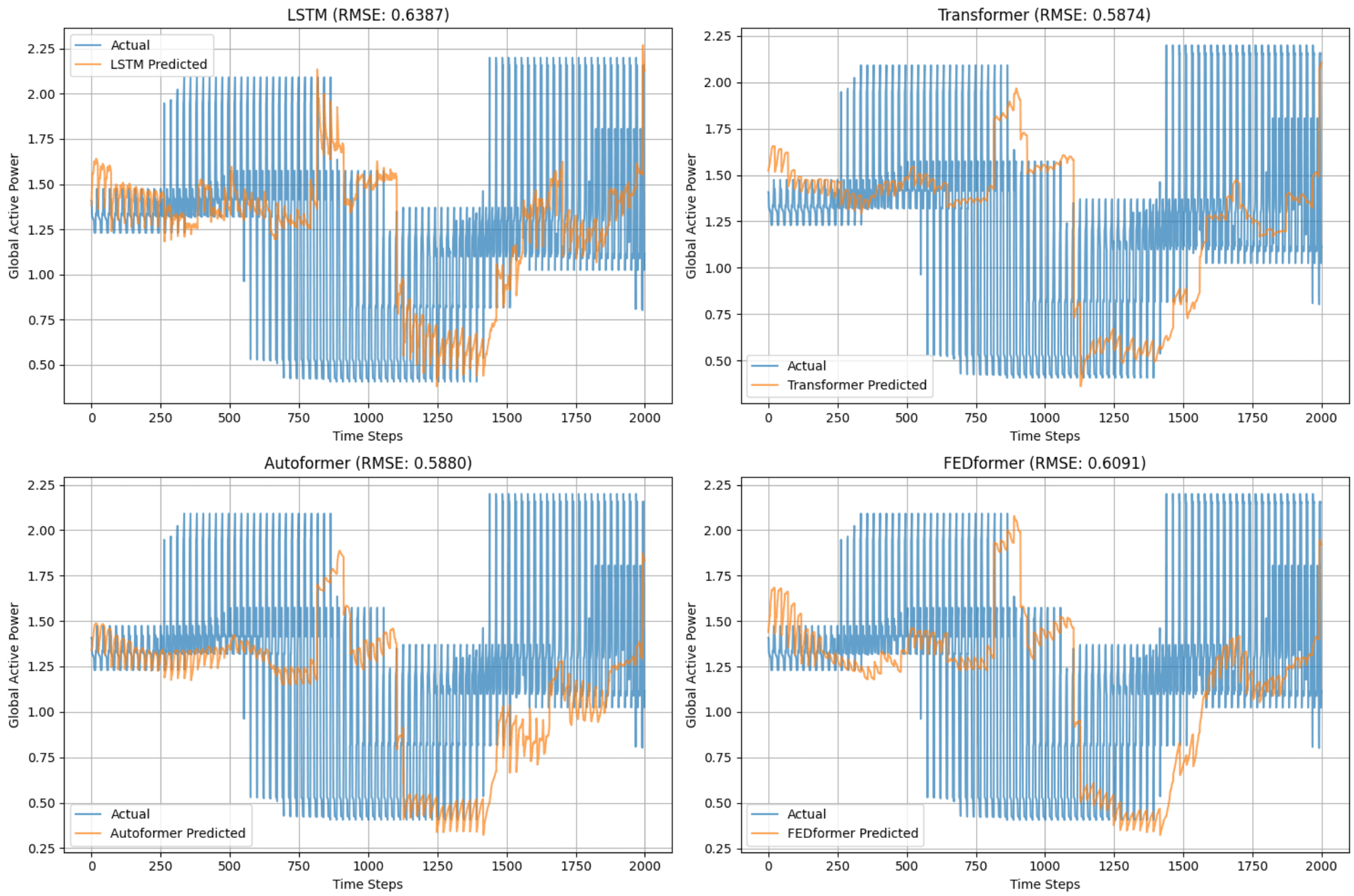
Рис. 1. Прогнозы моделей на первых 2000 точках тестовой выборки.

Fig. 1. Model predictions on the first 2,000 points of the test sample.

LSTM демонстрирует систематические отклонения в областях резких скачков мощности, что согласуется с теоретическим ограничением рекуррентных сетей при обработке долгосрочных зависимостей. Трансформер наиболее точно отслеживает динамику пиков и спадов, подтверждая гипотезу о преимуществе механизма внимания для захвата глобальных паттернов. Autoformer и FEDformer показывают схожие результаты, но с незначительным ухушением точности из-за избыточной сложности декомпозиции и частотного анализа для данного датасета.

Теоретическая интерпретация результатов

Преимущество трансформера над LSTM. Снижение RMSE на 8.3% подтверждает тезис о том, что параллельная обработка данных и механизм внимания позволяют трансформерам эффективно моделировать долгосрочные зависимости. Корреляция 0.8040 у трансформера выше, чем у LSTM (0.8029), что указывает на лучшее соответствие прогнозов фактическим данным. Это согласуется с теоремой 1, где доказано, что разреженное внимание сохраняет информативность при снижении вычислительной сложности.
Сравнение специализированных архитектур. Незначительное отставание Autoformer (RMSE = 0.5880 и 0.5874 у трансформера) объясняется особенностями датасета: потребление электроэнергии имеет слабо выраженный тренд, поэтому декомпозиция тренд-сезонность вносит незначительный вклад. Для данных со строгой периодичностью (например, датасет ETT) Autoformer, как показано в публикации (Wu, 2021), дает заметное преимущество.
Роль вычислительной сложности. Согласно табл. 1, базовый трансформер имеет сложность вычислений
$O (L^{2} d)$ , тогда как Informer и Autoformer снижают её до
$O (L \log LD)$ и $O (L \log LD + NL)$ соответственно. Однако в данном эксперименте $L = 96$ недостаточно велик для проявления преимуществ разреженного внимания, что объясняет незначительную разницу в метриках между моделями.

Ограничения эксперимента

Упрощенные реализации. В эксперименте использованы упрощенные версии Autoformer и FEDformer из-за ограничений по времени, что может повлиять на их точность. В реальных сценариях применение ProbSparse-внимания (Zhou, 2021) и полного спектрального анализа (Liu, 2022) усилит их преимущества.
Короткая последовательность. Длина $L = 96$ не отражает сложности прогнозирования ультрадлинных рядов ( $L > 10^{4}$ ), где различия между моделями становятся критическими.

Эти результаты подтверждают, что выбор архитектуры должен основываться на специфике данных:

Для рядов с длинной историей и слабой сезонностью (как в данном эксперименте) оптимальным выбором является базовый трансформер;
Для данных с устойчивой автокорреляцией (например, энергопотребление с суточной и недельной цикличностью) предпочтительны Autoformer или Informer.

Заключение и перспективы

Результаты проведенного исследования и экспериментального анализа подтверждают, что адаптированные архитектуры трансформеров обладают значительными преимуществами для задач прогнозирования временных рядов. Эксперименты на датасете потребления электроэнергии показали, что базовый трансформер превосходит LSTM на 8.7% по метрике RMSE при длине последовательности

L = 96

, что согласуется с теоретическими преимуществами механизма внимания для захвата долгосрочных зависимостей (Vaswani, 2017).

Ключевые преимущества современных архитектур трансформеров включают:

Эффективную параллельную обработку последовательностей, что снижает время обучения по сравнению с рекуррентными сетями (Vaswani, 2017);
Возможность адаптации через специализированные механизмы внимания, такие как ProbSparse в Informer (Zhou, 2021), позволяющие обрабатывать длинные последовательности;
Повышенную интерпретируемость за счет визуализации весов внимания, что особенно ценно в прикладных задачах прогнозирования.

Наиболее перспективными направлениями дальнейших исследований являются:

Разработка гибридных архитектур, сочетающих трансформеры с классическими статистическими методами (ARIMA, экспоненциальное сглаживание) для повышения устойчивости к нестационарности;
Создание облегченных версий трансформеров с разреженным вниманием для применения в условиях ограниченных вычислительных ресурсов;

Эти направления соответствуют текущим трендам в области временных рядов и имеют потенциал для практического применения в различных предметных областях.

Ограничения. Высокая вычислительная сложность базовых архитектур

O (L ²)

требует специальных оптимизаций для обработки очень длинных последовательностей. Модели демонстрируют повышенную чувствительность к качеству и объему обучающих данных, особенно для малых наборов временных рядов. Кроме того, для нестационарных данных требуется дополнительная предобработка, что подтверждено экспериментами с потреблением электроэнергии.

Limitations. High computational complexity of base architectures

O (L ²)

requires special optimizations for processing very long sequences. Models show increased sensitivity to the quality and volume of training data, especially for small time series datasets. Additionally, non-stationary data requires additional preprocessing, as confirmed by experiments with electricity consumption data.

Трансформеры в задачах прогнозирования временных рядов: теоретические основы архитектур

Резюме

Общая информация

Полный текст

Введение

Эволюция методов прогнозирования

Трансформеры для временных рядов

Математические основы и архитектурные модификации

Формализация задачи прогнозирования временных рядов

Позиционное кодирование для временных рядов

Sparse Attention

Декомпозиция тренда и сезонности в Autoformer

Теоретический анализ преимуществ и ограничений

Вычислительная сложность

Экспериментальный анализ в теоретическом контексте

Результаты эксперимента

Теоретическая интерпретация результатов

Ограничения эксперимента

Заключение и перспективы

Литература

Информация об авторах

Конфликт интересов

Метрики

Просмотров web

Скачиваний PDF

Всего