Курс математики ставит своей целью формирование у школьников предпосылок теоретического мышления (анализ, планирование, рефлексия), поэтому он ориентирован главным образом на формирование научных (математических) понятий, а не только на выработку практических навыков и умений. Эта специфика курса требует особой организации учебной деятельности школьников в форме постановки и решения ими учебных задач [1, 2, 3].
Учебной называется такая практическая задача, которая вынуждает ученика искать общий способ решения всех задач данного типа.
Учебная задача существенно отличается от многообразных частных задач. При решении последних школьники овладевают частными способами и лишь при длительной тренировке они усваивают некоторый общий способ. Усвоение этого способа происходит по эмпирическому принципу движения мысли от частного к формально общему. При решении же учебной задачи школьники первоначально овладевают содержательным общим способом, а затем применяют его к каждой частной задаче. Решение учебной задачи осуществляется согласно теоретическому принципу, который имеет значение не только для некоторого частного случая, но и для всех случаев данного типа. Мысль школьников при этом движется от общего к частному.
При решении учебной задачи выполняются следующие учебные действия:
1) преобразование условий задачи с целью обнаружения всеобщего отношения изучаемого объекта;
2) моделирование выделенного отношения в предметной, графической или буквенной форме;
3) преобразование модели отношения для изучения его свойств в «чистом» виде;
4) построение системы частных задач, решаемых общим способом;
5) контроль за выполнением предыдущих действий;
6) оценка усвоения общего способа как результата решения данной учебной задачи.
Основным содержанием настоящего курса служит понятие действительного числа, которое является стержневым для всей школьной математики. Это понятие, в свою очередь, базируется на понятии величины. Генетически исходным отношением, порождающим все виды действительного числа, является отношение величин, получаемое в результате измерения одной величины с помощью другой, принятой в качестве единицы измерения — «мерки». Натуральное число как исходная форма этого отношения, отражающая последовательное «укладывание» мерки в измеряемой величине, а также другие виды действительного числа дети получают при решении одной и той же задачи — задачи построения величины, равной заданной (задачи воспроизведения величины); меняются лишь условия задачи, что и определяет различия видов числа и способов его обозначения.
Так как в дошкольной жизни ребенка фактически нет опыта действий с непрерывными величинами, то курс математики начинается с изучения величин и отношений между ними.
В простейшем случае задача воспроизведения величины решается выбором предмета, равного данному по определенному признаку. Действуя с различными предметами, пытаясь заменить один предмет другим, подходящим по заданному признаку, дети выделяют параметры вещей, являющиеся величинами, т. е. свойства, для которых можно установить отношения «равно», «неравно», «больше», «меньше». При этом выделение каждой конкретной величины в первую очередь связано с овладением детьми определенным способом сравнения предметов и лишь во вторую со словом-термином. Так, представления о длине дети получают, прикладывая предметы определенным образом друг к другу; о площади — совмещая плоские предметы друг с другом (сначала непосредственно, а затем с разделением на части и перегруппировкой частей); об объеме как о «емкости» вещей — переливая воду из одного сосуда в другой. Понятие массы возникает в связи со взвешиванием предметов.
Отношения, полученные в результате сравнения предметов, моделируются сначала с помощью других предметов и графически (отрезками), а затем буквенными формулами. Это позволяет отделить отношения от способов их обнаружения, специфичных для разных конкретных величин, и перейти к рассмотрению общего понятия величины, т. е. к исследованию свойств отношений «равно», «больше», «меньше» в «чистом» виде.
Решая задачи по упорядочиванию величин (поиск самой большой или самой маленькой величины), дети устанавливают формальные свойства отношений «равно», «больше», «меньше» (например, транзитивность). Это позволяет им получать результаты сравнения величин не только с помощью предметных действий, но и путем логического вывода.
Более сложным случаем воспроизведения величины является уравнивание — одной величины до другой. Изучение условий перехода от неравенства к равенству приводит к необходимости уточнения простого сравнения величин разностным и введения действий сложения и вычитания величин. Таким образом, действия сложения и вычитания, а также их свойства вводятся еще в «дочисловом» периоде обучения. Эти действия моделируются графически и с помощью буквенных выражений. При этом выражения одновременно выступают и как описание действий, и как обозначения величин-результатов этих действий.
Последующее усложнение условий задачи воспроизведения величин (пространственная или временная разделенность образца и материала) требует нового способа ее решения. Величина в этом случае воспроизводится с помощью своей правильной части (мерки), которая повторяется в ней некоторое число раз. При этом у детей формируется понятие числа не как совокупности отдельностей (что характерно для традиционного обучения), а как инструмента счета, позволяющего получать из одной величины другие. Действия измерения-отмеривания моделируются с помощью функционального знака ^ (стрелки) в схемах вида:
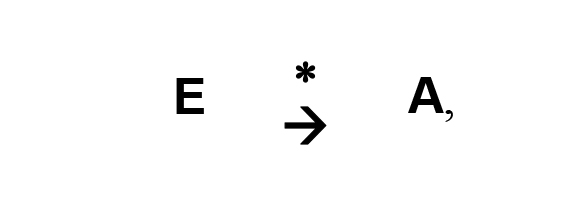
где Е — обозначение мерки, А — обозначение измеряемой или отмеряемой величины, * — код способа построения величины, т. е. та или иная форма числа.
Введение стрелочных схем позволяет различить и представить в общем виде три типа задач, связанных с задачей воспроизведения:
1) построение (отмеривание) величины по заданным мерке и числу;
2) измерение величины — нахождение числа по заданным величине и мерке;
3) поиск мерки, с помощью которой было произведено измерение данной величины.
Вопрос о записи чисел приводит к необходимости введения цифр. Наряду с арабскими дети знакомятся с цифрами разных народов, а также с так называемыми сказочными цифрами (искусственными системами значков). Это позволяет отделить в понимании детей суть числа, которая заключена в способе действия с величинами, от знака, которым число обозначается.
Процесс измерения-отмеривания, как потенциально бесконечное прибавление одной и той же величины (мерки), моделируется с помощью числовой прямой. Представление чисел в виде отрезков и точек числовой прямой позволяет «оторвать» числа от конкретных действий измерения и отмеривания величин и рассматривать их как самостоятельные объекты, над которыми также можно производить действия. Выясняется, что по отношению к числам могут быть поставлены те же задачи, что и для величин, в частности задача сравнения.
Сравнение чисел, в свою очередь, позволяет расширить возможности сравнения величин. Теперь уже нет необходимости в построении самих сравниваемых величин, достаточно знать, сколько раз одна и та же мерка уместилась в этих величинах, т. е. их числовые значения. Таким образом, выявляется новый аспект числа — количественный, выражающий результативную сторону счета. При этом количественный аспект числа рассматривается более широко, чем это принято в традиционном обучении, где он связан только с поэлементным пересчетом совокупностей. Здесь счет выступает моментом измерения произвольной величины любой меркой. В частности, и присчет совокупности может вестись не только штуками, но и парами, тройками и т. д. Таким образом, число, как характеристика величины, зависит не только от самой этой величины, но и от выбранной мерки (единицы измерения), т. е. представляет собой отношение (связь) между величинами. Этот новый смысл числа выражается формулой вида:

где А — величина, Е — мерка, п — числовое значение А относительно Е.
Кроме того, рассматривается еще один вид формул:
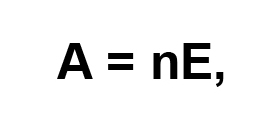
отвечающий представлению величины с помощью своего числового значения (именованного числа). Изучение условий перехода от сравнения величин к сравнению их числовых значений и наоборот открывает для детей важность задачи измерения всех величин (одного рода) одной и той же меркой. А это, в свою очередь, приводит к пониманию назначения стандартных единиц измерения и недостаточности имеющихся в их распоряжении натуральных чисел. Итак, понимание числа как отношения величин «отрывается» от определенного способа измерения величин (последовательного прибавления мерки), что позволяет говорить о числе вообще (точнее, о положительном действительном числе). Это общее понимание числа закрепляется в модели (на числовой прямой) и в буквенных обозначениях чисел.
Изучение действий сложения и вычитания чисел связано с анализом отношения «частей и целого» для величин. Дети учатся выделять компоненты этого отношения, рассматривая их как предметные ситуации, так и их текстовые описания. Выделенное отношение «частей и целого» моделируется с помощью схем, чертежей и различных формул, выражающих зависимость одного из компонентов отношения от двух других. При переходе от описания ситуаций к текстовым задачам формулы превращаются в уравнения за счет введения буквы, «икс» (х), обозначающей искомое (неизвестное) значение величины. В ходе этой работы дети также усваивают состав чисел в пределах 10 и связанные с этим табличные случаи сложения и вычитания чисел.
Далее рассматривается вопрос об ограниченности любого запаса знаков (слов, цифр), служащих для обозначения чисел. Он формируется для детей как задача воспроизведения величины с помощью одной заданной мерки в ситуации, когда считать можно только до определенного числа. Решение этой задачи приводит детей к открытию нового способа измерения — отмеривания с помощью системы вспомогательных (дополнительных) мерок, полученных из основной. Каждый раз, когда «укладывание» очередной мерки в величину доходит до последнего возможного при счете числа, все отложенные мерки образуют новую следующую мерку системы и измерение начинается с нее. В этом случае отношение между соседними мерками системы остается постоянным, оно равно основанию системы счисления (последнему возможному при счете числу), а сама система мерок является открытой, т. е. при необходимости всегда может быть продолжена.
Такой способ измерения требует особой формы представления числа-результата измерения, оно представляется набором знаков (цифр), где каждый знак выражает результат измерения одной определенной меркой системы. Это так называемое многозначное число. Вначале многозначное число представляется в известном детям табличном виде, а затем происходит переход к новому позиционному способу записи, где смысл каждого знака (цифры) определяется его местом (позицией) в записи.
Многозначные числа моделируются на числовой прямой, что позволяет детям осознать их как форму числа, а не как набор отдельных знаков. Кроме того, изображение многозначных чисел на числовой прямой дает универсальный, хотя и трудоемкий, способ сравнения многозначных чисел, представленных в разных системах счисления. Рационализируя действие сравнения многозначных чисел, дети устанавливают, что для чисел, данных в одной системе счисления, применим поразрядный (позиционный) способ сравнения. Десятичная система счисления рассматривается как частный случай позиционной. К концу I класса дети знакомятся с произвольными многозначными числами, заданными в разных системах счисления, хотя чтение чисел ограничивается четырехзначными числами в десятичной системе счисления.
В такой логике во II и III классах продолжается изучение многозначных чисел и действий с ними. В настоящее время разработана программа и готовятся методические пособия для V и VI классов.
В результате обучения у детей к концу начальной школы формируется умение анализировать типологические особенности арифметических задач, осознанно выбирать соответствующий способ их решения, целенаправленно строить последовательность действий по решению частной задачи общим способом. То есть у детей возникают предпосылки теоретического мышления.
Основные темы курса:
I класс
1. Величины и отношения между ними.
2. Введение числа.
3. Отношение частей и целого.
4. Системы мерок.
5. Позиционные системы счисления.
II класс
1. Сложение и вычитание многозначных чисел.
2. Умножение и деление чисел.
3. Сочетательный закон умножения.
4. Распределительные законы.
III класс
1. Умножение и деление многозначных чисел.
2. Анализ текстовых задач.
3. Прямая пропорциональная зависимость величин.
4. Обыкновенные дроби.
V и VI классы
1. Величины.
2. Отношения между однородными величинами.
3. Прямая пропорциональная зависимость величин.
4. Величины и числа.
5. Обыкновенные дроби.
6. Позиционные дроби.
7. Действительные числа.
8. Положительные и отрицательные числа.