Курс развивающего обучения математике для четырехлетней начальной школы

Представленный в статье вариант курса развивающего обучения математике имеет ряд особенностей. Целью курса является обучение детей с 6-ти лет, поэтому нем более развернуто представлены этапы формирования учебных действий. Усилено внимание к формированию навыков решения текстовых задач. Результаты тестов и проверки знаний и умений учащихся показали, что в развитии мышления и учебной деятельности они продвинулись значительнее, чем их сверстники, обучавшиеся по общепринятой методике.

Психологические исследования показывают, что у младших школьников формирование понятий происходит через выполнение ими учебного действия моделирования. Общепринятая методика, кик правило, не предусматривает моделирования, а пытается сформировать обобщения у детей введением формулировок разного рода правил и многократным повторением конкретных действий с конкретными объектами. В результате несколько учеников в классе (так называемые способные) действительно приходят к содержательному обобщению, но большинство ребят осваивают лишь умение манипулировать правилами.

Особенности процесса формирования действия моделирования у шестилетних школьников уже описывались нами [2]. Здесь же мы приведем примеры функционирования некоторых средств моделирования. Одним из них является абстрактная символика: сначала это произвольные знаки — «сказочные цифры», а затем буквы. Как это ни покажется невероятным для сторонников традиционной методики, абстрактная символика воспринимается школьниками легко. По нашей методике это происходит на 19-м уроке первого года обучения [2]. Появление символики позволяет затем ставить перед детьми задачи, нацеленные на обобщение учебного материала в форме конкретных заданий.

Так, учащимся предъявляется «оборванная» с двух сторон лента, на которой «сказочными цифрами» записан отрезок числового ряда. Неизвестно конкретное значение Цифр, но известно, что ряд построен по тем же правилам, что и обычный. Предлагается записать «по-сказочному» значения нескольких выражений:

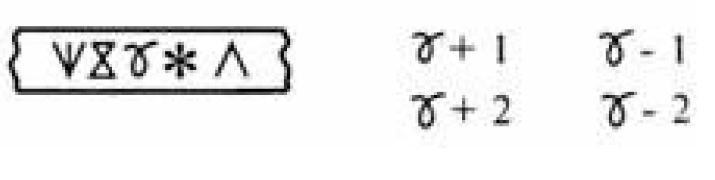
Выполнение таких заданий требует от учащихся актуализации общей идеи порядка и способствует усвоению принципа ее использования в вычислительных операциях. Заметим, что «сказочные цифры» не требуется запоминать. Зачастую учащимся предлагается самим придумать знаки и установить их порядок в отрезке числового ряда.

Приведем примеры использования абстрактной символики в заданиях на освоение позиционного принципа построения многозначных чисел и их разрядного состава. В первой группе заданий требуется сравнить числа в каждой паре, во второй — определить знамения выражений.

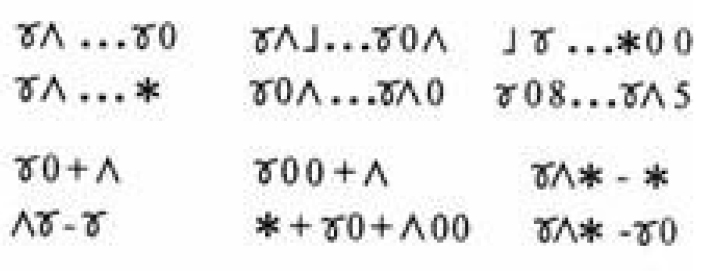
Задания с абстрактной символикой, с одной стороны, требуют от учащихся обобщения, а с другой создают определенные условия для его осуществления. Аналогично используются и конкретные числа, но подобранные таким образом, чтобы ученики не могли выполнить неосознанных вычислений. Так, первоклассники часто не в состоянии прийти к общему способу действия при решении текстовых арифметических задач в силу того, что, сталкиваясь с «маленькими» числами, использованными в сюжетах, могут получить ответ не в результате анализа отношений, заложенных в условии задачи, а при манипулировании числами. Оказывается, что замена в задачах однозначных чисел двузначными мобилизует мышление первоклассника на оценку отношений и выбор арифметического действия (которое затем может быть выполнено на калькуляторе).

Конечно, в определенных случаях одной мобилизации недостаточно, и тогда для формирования обобщения требуется прибегнуть к использованию других средств моделирования, в частности к пространственно-графическим построениям-чертежам. Осваивая форму чертежа, ученики выделяют фиксируемое им отношение, а преобразовывая чертеж, выявляют общие свойства отношения и их частные следствия. Покажем это на примере изучения свойств отношения целого и частей (в I классе).

Предметные действия увеличения и уменьшения объема исходных совокупностей (выполняемые с неопределенными количествами объектов) фиксируются в тетрадях прямоугольниками, которые как бы загораживают объекты счетных действий (см. рис. ниже). В полученном чертеже выделяются целое и части. При подборе их конкретных значений выясняется, что целое всегда больше своей части, что значения двух элементов отношения однозначно определяют значение третьего и, наконец, что значение целого вычисляется сложением, а части — вычитанием. Далее, простейший сюжет, фиксированный чертежом, перестраивается в три задачи, так как значение каждого из трех элементов сюжета можно определить по значениям двух других.

Таким образом, учащиеся переходят от изучения общих свойств отношения целого и частей к построению и решению текстовых задач. Один из этапов этого процесса может получить в тетрадях учащихся следующий вид:

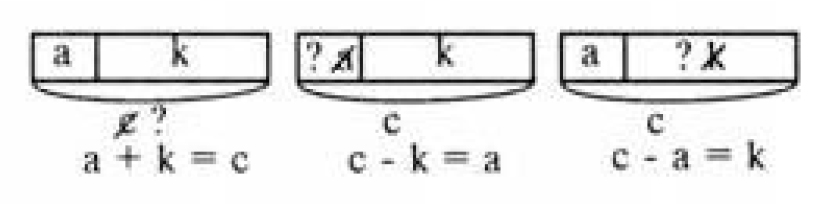
Приведенная форма чертежа в дальнейшем постепенно преобразуется сначала при рассмотрении свойств разностного отношения, затем при введении ситуаций, связанных с действиями умножения и деления, наконец, уточняется для случаев кратного сравнения двух отдельных совокупностей. С помощью условных графических построений и перестроений удается, с одной стороны, обусловить выбор арифметического действия свойствами отношения, а с другой — проследить характер связи между самими арифметическими действиями.

Отметим некоторые особенности учебно-методического комплекта, реализующего предлагаемый курс обучения. Комплект состоит из методического пособия «Учим понимать математику» [6, 7] и учебника-тетради «Учимся понимать математику» [3, 4, 5]. Значительное число упражнений в учебнике помечено знаком «ловушки», который предупреждает, что среди заданий имеется такое, для выполнения которого недостаточно определены условия. Эти задания важны для формирования у школьников учебных действий контроля и оценки. Есть упражнения, помеченные «звездочкой». Их могут выполнять самостоятельно сильные учащиеся (или желающие попробовать свои силы).

Многие задания (особенно со «сказочными цифрами») можно использовать при работе по любым программам, причем в качестве как обучающих, так и диагностирующих.

Предлагаемый вариант методики РО опробовался в течение 8 лет. В экспериментальных классах обучалось в среднем по 27 учеников, зачисленных в школу в возрасте 6 лет без какого-либо отбора. Результаты психологических тестов, а также итоги проверок качества и объема математических умений учащихся показали, что в развитии мышления и учебной деятельности они продвинулись значительнее, чем их сверстники, обучавшиеся по общепринятой методике.

 

 

 

1. Давыдов В. В., Горбов С. Ф., Микулина Г. Г., Савельева О. В. Обучение математике: Методическое пособие. I класс трехлетней начальной школы. М., 1994.
2. Микулина Г. Г. Некоторые особенности формирования действия моделирования при обучении математике детей шести лет // Психологическая наука и образование. 1996. № 1.
3. Микулина Г. Г. Учимся понимать математику. I класс (I-IV). М., 1995.
4. Микулина Г. Г. Математика. II класс (I-IV). Часть I. M., 1996.
5. Микулина Г. Г. Математика. II класс (I-IV). Часть II. М., 1996.
6. Микулина Г. Г. Учим понимать математику: Пособие для учителя. I класс (I-IV). М., 1995.
7. Микулина Г. Г. Учим понимать математику: Пособие для учителя. II класс (I-IV). М., 1996.