Психологические метаморфозы одной метафоры

В 1885 г. Г. Эббингауз обнаружил ряд весьма важных психологических закономерностей, которые впоследствии получили широкую известность как эббингаузовские «кривые научения». Данные кривые, которые, по существу, являются моделями — аналогами процесса выработки навыка, отражают ту закономерность, что многократные повторения приводят к улучшению качества выполнения задачи. В определенный момент рост качества достигает уровня, на котором фиксируется некоторое постоянство параметра, — происходит «выход на плато» (асимптоту). Момент «выхода на плато» можно назвать научением. В определенной мере кривые Эббингауза отражают известную народную мудрость: «Повторение — мать учения». Безусловно, в этой пословице заложен глубокий дидактический смысл, отражающий роль упражнений в механизме научения. Оказывается, помимо дидактического смысла в данной метафоре содержится еще весьма интересное содержание.

Проводя эксперименты с детьми младшего школьного возраста, мы обнаружили некоторые тенденции, принимающие характер определенной закономерности. Эксперименты проводились с детьми 5-6, 8 и 9 лет. В общей сложности нами исследованы три выборки испытуемых дошкольного и младшего школьного возраста. Объем отдельной выборки состоял из 50 испытуемых. Детям предлагалось 10 заданий на решение однотипных задач на обобщение. В каждом задании предъявлялось 20 геометрических фигур, 5 из которых имели общие признаки, а оставшиеся 15 выступали в качестве «фоновых». Время, за которое ребенку предлагалось отыскать фигуры, подлежащие объединению, и произвести соответствующее обобщение, фиксировалось. Напомним, что предлагаемые задачи были однотипными, т. е. если в одной серии ребенок производил обобщение с треугольниками, то в другой — с квадратами или ромбами. При изменении последовательности предъявления заданий мы обнаружили неизменность результатов по фиксируемому времени выполнения, что подтверждает однотипность задач эксперимента.

Отмечая время, затрачиваемое на выполнение заданий, мы ожидали постепенного уменьшения его количества, поскольку от серии к серии ребенком присваивался способ выполнения задачи, что, очевидно, должно сказаться на улучшении качества параметра времени — на быстроте выполнения задания. Однако в данном случае оказалось, что время изменяется нелинейно: оно то уменьшается, то опять увеличивается. При этом возникают маятникоподобные колебания количества затрачиваемого испытуемым времени с постепенным угасанием амплитуды данных колебаний. Проведя эксперименты на трех разновозрастных выборках, мы обнаружили следующую картину, которую отразили в соответствующих графиках по усредненным показателям времени для обследованных групп. По горизонтали представлены серии предъявленных заданий, по вертикали — время в секундах.

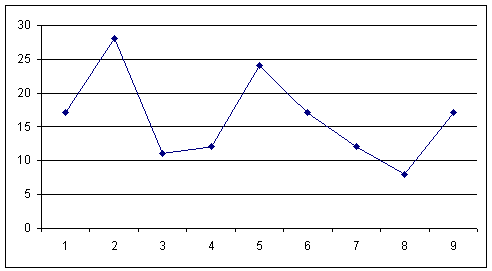
График 1. Результаты выполнения заданий детьми 5-6-летнего возраста

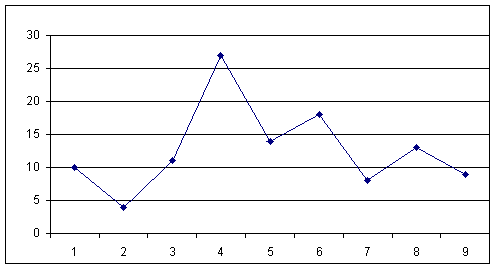
График 2. Результаты выполнения заданий 8-летними детьми

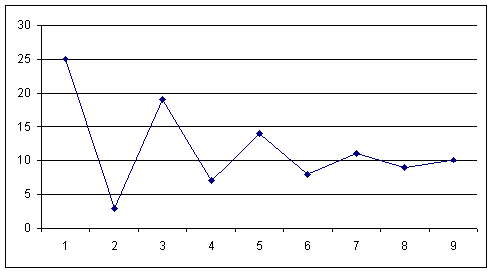
График 3. Результаты выполнения заданий 9-летними детьми

На основании полученных графиков можно предположить, что существует некоторая закономерность в изменениях амплитуды колебаний времени выполнения. Особым образом мы исследовали показатели третьей выборки, где наблюдается очевидная закономерность в изменениях времени выполнения заданий. При дальнейшем анализе результатов исследований в третьей группе мы попытались представить их в виде математической модели. Наиболее адекватной для результатов нашего исследования явилась модель логистической функции: X_n+1+1=λX_n (1—X_n). Данная модель широко используется в исследованиях самоорганизующихся сложных систем [7], проводимых в рамках междисциплинарного подхода, именуемого синергетикой. В рассматриваемой нами модели одним из ключевых в выражении самоорганизации является параметр, который, по существу, отражает степень зависимости поведения системы в данный момент от поведения в предыдущей серии. Для оптимального управления обучением, на наш взгляд, важен момент выхода системы на плато — постоянный уровень фиксируемого параметра. Этот уровень отражает момент самоорганизации процесса. При определенной методике апроксимации результатов можно вычислить индивидуальный показатель выхода на плато для отдельного испытуемого, что будет отражать специфику самоорганизации его мышления. Как показал наш эксперимент, при решении однотипных задач не происходит простого присвоения способа их выполнения. Возникает некоторый инкубационный период присвоения способа решения, поэтому существует востребованность в упражнениях, имманентная процессу мышления.

На нелинейность процесса научения, где допускаются и признаются закономерными временные ухудшения контрольных показателей, указывалось в исследовании В.Ф. Венды [4]. Однако автор объяснял причину ухудшения параметра внутренними трансформациями в стратегии обучения. Он выступил с критикой классических кривых научения и выдвинул свою концепцию существования динамических кривых научения, где есть и эволюционные, и трансформационные фазы. Нам неизвестно дальнейшее развитие трансформационной теории, в данной же работе, сославшись на частное исследование, нам хотелось бы подчеркнуть тот факт, что нелинейный характер закономерностей индивидуального обучения в той или иной форме обсуждался и ранее. Однако эта проблема не находила своего решения в конкретных экспериментальных исследованиях, проводимых в педагогической психологии, в психологии развития.

Если принять идею С. Л. Рубинштейна [8], А.В. Брушлинского [3] о процессуальности мышления, то символическое выражение данного процесса будет обозначено в виде системы. Система в силу информационного обмена со средой будет открытой, энтропия (степень хаоса), соответственно, будет в ней расти. Этот процесс, по основному положению А.В. Брушлинского, «недизъюнктивен». Рост энтропии в системе обозначает ее сложность и вероятность возникновения самоорганизации. Поскольку мы обратились к методу моделирования, хотелось бы вспомнить замечательное в своей конкретности высказывание А.В. Брушлинского относительно моделирования в психологии мышления, который пишет, что «моделями считаются, и во многом справедливо, лишь математические уравнения, которые описывают изучаемый процесс» [3, с. 185].

Результаты нашего эксперимента позволяют иначе взглянуть на смысл пословицы «Повторение — мать учения». Очевидно, что для усвоения способа выполнения задания необходимы повторения. Повторения служат росту насыщенности информации относительно способа выполнения задачи, при достижении определенного уровня этой насыщенности и возникает самоорганизация. Повторение несет в себе информацию для системы. Мышление в данном случае выступает как недизъюнктивный процесс, динамика которого существует на протяжении определенного периода спонтанного присвоения способа выполнения.

Метаморфоза рассматриваемой нами пословицы заключается, на наш взгляд, в психологическом перевоплощении ее дидактического смысла в синергетический. Более того, метаморфоза эта может заключаться в кардинальной трансформации данной пословицы в иную, ничем не уступающую по глубине своей и синергетической направленности. В данном случае имеется в виду широко известная пословица «Семь раз отмерь…», (см. график 3).

Исходя из метафорических размышлений о роли повторений, спроецированных на описанные выше эксперименты, следует по-иному взглянуть на эффективность интенсивных технологий в обучении. Синергетический контекст динамики процесса предполагает наличие некоторого инкубационного периода, во время которого происходит самоорганизация как необходимое условие научения. Традиции нашей сегодняшней педагогики ориентированы на быстроту, интенсификацию, которые, очевидно, являются следствием взрослоцентрированной образовательной культуры. В небезызвестной пословице «Поспешишь — людей насмешишь», вероятно, имеется в виду не суета осмеянного толпой человека, а величие степенной неторопливости, которая, как правило, и в фольклоре оценивается позитивно.

Синергетический контекст упомянутых нами пословиц наводит на размышления о темпе обучения. Темп усвоения — это не только показатель продуктивности обучения, но и условие оптимального управления данным процессом. Когда мы говорим, что существует самоорганизация в процессе мышления, то предполагаем, что мышление имеет внутреннюю спонтанную тенденцию, однозначно не детерминированную внешним воздействием. О необходимости пересмотра темпов обучения говорят и методисты по отдельным школьным предметам. Например, в одной из статей, автором которой является учитель, создатель известных учебников по математике, В.К. Совайленко, высказывается глубокое сожаление об изменениях в методике преподавания математики, предпринятых в современной школе, и отмечается ряд ошибочных мер, введенных в ходе модернизаций начиная с 60-х гг. минувшего столетия. В рассматриваемом нами контексте хотелось бы обратить внимание на два замечания упомянутого автора:

1. «в прежних программах по математике в начале учебного года отводи лось до 32 часов на повторение. Но в 1955 году без всякой экспериментальной проверки эти часы были сняты, что и породило массовую посредственную успеваемость»;
2. «задачи «систематизировались» однородными группами, что позволяло усваивать общие методы их решения. В 70-е гг. практика типовых задач была отвергнута и их стали располагать в смешанном порядке. Это лишило учащихся возможности научиться решать задачи…» [9, с. 36—37].

Думается, в идее о «повторении как матери учения» речь идет не об оптимизации памяти в ходе повторения и даже не о роли упражнений при выработке навыка, метафора эта затрагивает гораздо более глубокие, когнитивные пласты человеческого познания. Мышлению как процессу необходимо время для внутренней самоорганизации. Лишь при определенном количестве повторений происходит истинное присвоение способа решения, который становится имманентным мыслительному процессу. В связи с синергетическим видением обучения возникает аналогия с теорией Л.С. Выготского о зоне ближайшего развития. Л.С. Выготский выступает с тезисом относительно того, что умственное развитие ребенка следует измерять через динамику его успехов в обучении. Эта идея созвучна обозначенной нами выше проблеме синергетического подхода к исследованию мышления как процесса. Невозможно не вспомнить слова О. М. Дьяченко о том, что «неоднократное обращение к творчеству Л.С. Выготского позволяет увидеть новые грани уже, казалось бы, традиционных проблем, увидеть и новые проблемы, которые еще требуют своего теоретического и экспериментального анализа. Даже те вопросы, которые прямо Л.С. Выготский не решал, при чтении его работ освещаются особым сиянием подлинного творчества и напряженной человеческой мысли» [5, с. 110].

Настоящий этап развития проблем педагогической психологии ознаменован влиянием синергетики — новой методологии, рассматривающей психику как сложную открытую систему, субстанциональность которой обеспечивается самоорганизацией. Актуальность синергетического подхода в психологических исследованиях очевидна, так как он открывает новые принципы управления сложными нелинейными системами. По существу, синергетические идеи в психологии индуцируют возникновение новой парадигмы, сближающей естественнонаучный и гуманитарный подходы в исследованиях психических явлений  [6]. Синергетика привлекательна скрытым методологическим потенциалом, который в ближайшем будущем, на наш взгляд, выразится в совершенно новых подходах к исследованию сложного в самых различных областях психологии.

Таким образом, мы увидели новые грани проблем, связанных с управлением когнитивным развитием ребенка в контексте синергетической парадигмы [1, 2]. Синергетический смысл упражнений в обучении отличен от ставшего привычным дидактического: упражнения необходимы не столько для запоминания изучаемого материала и не для выработки навыка, они нужны для достижения сложной когнитивной системой человека режима самоорганизации, заключающегося в выходе отдельного параметра на плато. Зная закономерности самоорганизующейся системы, можно прогнозировать и оптимальное управление ею.

1. Баянова Л. Ф., Ярославова А. И. Диссипативные структуры в интеллекте их характеристики // Ежегодник Российского психологического общества. М., 2002. Т. 9. Вып. 2.
2. Баянова Л. Ф. О моделировании самоорганизации в когнитивной психологии // Синергия культуры: Труды Все российской конференции. Саратов 2002.
3. Брушлинский А. В. Психология мышления и кибернетика. М., 1970.
4. Венда В. Ф. Проблемы психологического анализа и моделирования динамики познавательного процесса // Психологические исследования познавательных процессов и личности. М 1983.
5. Дьяченко О. М. Проблема развития способностей: до и после Л. С. Выготского // Вопросы психологии. 1996 № 5.
6. Крылов В. Ю. Психосинергетика как возможная новая парадигма психологи ческой науки // Психологический журнал. 1998. Т.19. № 3.
7. Медведева Н. Б. Динамика логистической функции // Соросовский образовательный журнал. 2000. № 8.
8. Рубинштейн С. Л. Основы общей психологии: В 2 т. М., 1989.
9. Совайленко В. К. О содержании математического образования и качестве учебников (мнение учителя) // Педагогика. 2002. № 3.