Иниционно-семантическая модель дивергентной креативности

Автором проведен частотный анализ семантических категорий ответов испытуемых на задание дивергентного теста эмоциональной креативности Д.В. Ушакова и О.Н. Ивановой и построена семантическая сеть, показывающая статистику переходов в последовательностях ответов из категории в категорию. Рассмотрены структурные характеристики семантической сети, включая ее кластеризацию и ассортативность. На основе статистического анализа категориальной структуры ответов предложена новая двухфакторная иниционно-семантическая вероятностная модель продуцирования семантических категорий в ситуации тестирования дивергентной креативности. Ведущим фактором дивергентной креативности в модели является инициативность человека. Другой фактор связан с оригинальностью семантики ответов испытуемого. Вероятностные параметры модели определяются на основе обработки данных эталонной выборки. Введенные новые тестовые оценки являются расчетными и обеспечивают единообразное и соотнесенное с нормой вычисление индивидуальных показателей креативности, которые включают независимые друг от друга показатели иниционной креативности и семантической креативности, а также интегральный показатель креативности.

Совершенствование методов развития творческих способностей учащихся является важной задачей образовательного процесса и предполагает проведение психологических исследований, направленных на разработку адекватных моделей психических процессов и средств их психодиагностического тестирования. Тестовые модели при этом, по идее, должны учитывать как индивидуальные психологические качества, так и ситуативно­функциональные и социально-семантические характеристики тестовых ситуаций.

Характерным примером ситуационного тестирования являются тесты на дивергентное мышление [1]. Они связаны с продуцированием многочисленных семантически разных решений, относящихся к заданной нестандартной ситуации. Ответы испытуемых подвергаются категориальному анализу, и определяются индивидуальные значения ряда психологических факторов, которые так или иначе связаны с семантической новизной (это могут быть идеи, эмоции и др.), являющейся важным признаком творческого мышления.

В частности, в дивергентных тестах креативности принято различать довольно много параметров продуктивной активности испытуемых: беглость, гибкость, оригинальность [1; 8; 10] и др. Предложены были также новые специальные параметры, например: информационный показатель креативности [2; 7], показатель уникальности [2] и интегральный показатель творческого мышления [6]. Все эти параметры и показатели по их смыслу так или иначе определены на семантическом поле появления новизны и в этом отношении мало учитывают ситуационные контекстно-динамические психологические особенности поведения испытуемых.

Ниже приведен статистический анализ динамики формирования сети семантических категорий дивергентного теста эмоциональной креативности и на этой основе предложена новая двухфакторная иниционно-семантическая модель продуцирования тестовых ответов и новые расчетные показатели, характеризующие креативность.

Тест эмоциональной креативности и его семантическая сеть. Эмоциональная креативность представляет собой особый конструкт, который определяет творческую активность человека «на пространстве эмоционально окрашенного материала, т. е. в широком понимании представляет собой генерирование новых идей в отношении эмоциональных явлений» [5, c. 300]. Рассматриваемый в данной статье тест эмоциональной креативности Д.В. Ушакова и О.Н. Ивановой [5] предназначен для исследования творческой одаренности детей, начиная с 10-11 лет и до выпускных экзаменов в школе (17-18 лет). В качестве основного задания в тесте используется реакция на событие с каким-либо общеизвестным предметом. За определенное время испытуемым предлагается придумать как можно больше различных объяснений реакции человека на это событие и записать их на специальный бланк.

В рассматриваемом нами задании теста эмоциональной креативности испытуемому предлагается представить себе ситуацию и ответить на вопрос: «Друг вернул вам книгу, но у вас плохое настроение, почему?». Причем необходимо дать как можно больше вариантов ответов. Первичная выборка испытуемых составляет 198 человек. Результаты включают в себя довольно разнообразные ответы в количестве от 1 до 9. После классификации смысла ответов экспертом-психологом по качественным отличиям между ними было выделено 17 общих смысловых категорий, в которые попадают различные ответы всех испытуемых в выборке. Например, категория «книга испорчена» включает в себя ответы, связанные с разными повреждениями книги (вырванные листы, рисунки, грязь, запах и др.). Категория «книга не нужна» включает в себя ответы, связанные с причинами ненужности (нет времени для чтения, уже куплена новая книга и др.).

Категории теста эмоциональной креативности вместе со всей совокупностью переходов между ними образуют семантическую сеть, которая представляет собой информационную модель смысловой структуры предметной области и имеет вид ориентированного графа, вершины которого соответствуют категориям, а дуги (ребра) задают связи или отношения между ними. Эти отношения могут быть определены на основе анализа статистики переходов от узла к узлу.

В соответствии с активационной парадигмой семантической сети [3-5] процесс продуцирования ответов в тесте эмоциональной креативности можно представить в виде цепи вероятностных переходов по ориентированной сети (направленному графу). Сеть можно представить в виде графа, задав матрицу смежности размерности MxM, где М=17 - общее количество категорий. Плотность каждой из связей, заданных ребрами графа, определяется относительным количеством переходов по этой связи:

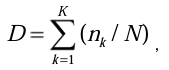
где N - здесь и далее общее количество испытуемых,

nk - число испытуемых, показывающих данную связь на k шаге,

K = 8 - общее число шагов.

Общий вид направленного графа семантической сети для системы из 17 категорий задания теста эмоциональной креативности представлен на рис. 1. Видно, что ряд узлов имеет значительно большее число связей, чем другие. При этом многие узлы часто повторяются. Значительное количество узлов не имеет взаимных связей или имеет только односторонние связи.

Анализ графа семантической сети позволяет сделать некоторые частные выводы, касающиеся семантики переходов от категории к категории. После выбора категории 9, связанной со сложностями общения между друзьями, очень вероятен переход к категории 1, означающей, что книга испорчена или ей нанесен какой-либо ущерб. Порча книги в свою очередь легко связывается с проблемами у героя из-за отсутствия книги (категория 8). Интересной семантически является в существенной мере «самодостаточная» категория 4 (книга не нужна). Идея ненужности книги имеет много аспектов и в то же время по самому смыслу мало связана с другими ситуационными смыслами, что, видимо, способствует большому числу «зацикленных» в ней переходов. Категория 2 (была возвращена другая книга) не только не имеет больших смысловых связей с другими категориями, но, похоже, также способствует разрушению контекста ситуации и тем самым прекращению (остановке) дальнейшей активности испытуемого.

В графе имеются как исходящие, так и входящие связи. Вне зависимости от направления связи два узла графа сети можно назвать соседями, если существует связь между ними. Для сложных сетей характерно, что два узла, соседних по отношению к какому- либо узлу, также являются соседями между собой. Это явление характеризуется кластерным коэффициентом Cli узла i. Кластерный коэффициент узла i вычисляется по формуле:

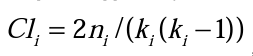
где ki - степень узла (число его соседей),

ni - число связей между соседями узла i.

Кластерные коэффициенты узлов сети характеризуют число связей между соседями этих узлов. Усредненный по всем узлам сети кластерный коэффициент С1 называется кластерным коэффициентом сети. В данном случае С1 = 0,72, т. е. сеть является достаточно сильно взаимосвязанной.

Коэффициент корреляции Пирсона между степенями соседних узлов называется коэффициентом ассортативности A и характеризует степень взаимной связи узлов с разными степенями. В сети возможна ситуация, когда узлы, имеющие большую степень, преимущественно связаны с узлами, тоже имеющими большую степень. Такие сети называют ассортативными. Для ассортативных сетей A > 0, для дисассортативных сетей A < 0. У сетей, не имеющих выраженной ассортативности, A близко к нулю [9].

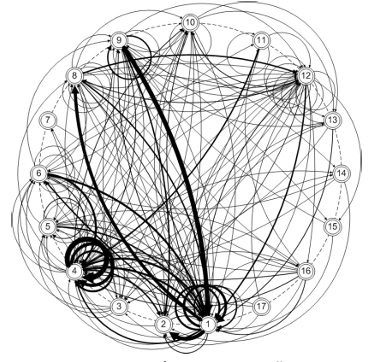
Рис. 1. Общий вид направленного графа семантической сети из 17 узлов -категорий теста (толщина линий примерно соответствует плотности связей)

В данном случае результат A = -0,22, т. е. сеть получилась немного дисассортативной. Это, в принципе, означает, что узлы с большим количеством связей связаны не столько между собой, сколько с узлами с малым числом связей. Такого рода зависимость, например, очень четко выражена в больших Интернет-сетях, где узлы с большим количеством связей имеют по большей части соединения с узлами с малым числом связей, и наоборот. Но в целом это характерно для больших отрицательных значений A.

Полученное достаточно близкое к нулю значение A означает, что система семантических категорий для данного задания теста является сложно связанной (сильно смешанной) и лишь в незначительной мере разделяется на два кластера более общих и менее общих категорий. Для наглядности на рис. 2 приведен график соотношения степеней узлов (отложена по оси абсцисс) со средней величиной степеней всех соседей этих узлов (отложена по оси ординат).

 

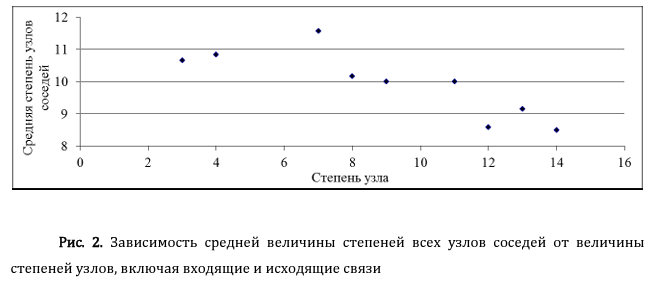
Для узла с заданной степенью можно определить среднюю степень его соседей. Видно, что в сети имеется слабая дисассортативная тенденция уменьшения степени соседей узла при увеличении степени самого узла. Однако эта тенденция очень незначительная и практически у узлов со всеми количествами связей наблюдается большое количество соседей. При этом полностью отсутствуют узлы с малым числом связей (менее трех). Топология такой (когнитивной семантической) сети отличается большей сложностью от собственно ассортативных или дисассортативных сетей [9] и, видимо, может свидетельствовать о существенной степени случайности происходящих в ней процессов. Моделирование вероятностей переходов в семантической сети. Динамика переходов из категории в категорию по графу рассмотренной выше сети может быть представлена в виде дискретного случайного процесса, моделирование которого представляет определенные трудности в силу недостаточного понимания сути психологических процессов, связанных с творчеством и мышлением. Гипотетические особенности активационной организации семантической памяти и процессы ассоциативного распространения в ней активности [3-5] свидетельствуют в пользу того, что вероятность продуцирования испытуемым на каждом шаге ответов в той или иной семантической категории в существенной мере должна зависеть от предыдущего и всех имевших место ранее шагов. На то, что семантика выбранных категорий влияет на переходы в другие категории, указывает и проведенный выше анализ графа семантической сети.

Вместе с тем сравнение распределений частот выбора категорий для нескольких первых шагов показывает, что при всех амплитудных различиях эти распределения имеют очень схожую форму. Расчеты парных корреляций между количествами ответов в разных категориях для первых трех шагов показывают, что коэффициенты корреляции Спирмана имеют достаточно большие значения (0,75;  0,77;   0,75) при уровне значимости 0,01.

Дополнительная проверка для случая в два раза большей выборки показывает, коэффициенты корреляции увеличиваются, достигая уровня 0,8 - 0,9. Этот факт наводит на мысль о том, что активационная динамика системы семантической памяти может быть обусловлена другими механизмами, например общей интенционально-конкурентной активацией этой системы. Это позволяет предположить, что в первом приближении продуцирование категорий ответов может осуществляться на каждом шаге случайным образом независимо от предыдущих шагов.

Тогда формула для эмпирического расчета общей вероятности Pg получить заданную последовательность категорий в ответах испытуемого представляет собой произведение частотных оценок вероятностей случайного выбора этих категорий в каждом из шагов последовательности:

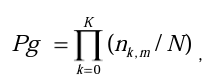
где nk,m - количество испытуемых, имеющих, как и данный испытуемый, ответ в m категории на k шаге (первый ответ теста считается нулевым шагом), K = 8.

Для того чтобы расчеты по этой формуле были адекватными по отношению к целостности выборки, при вычислении пошаговых частот необходимо учитывать и случаи отсутствия ответов, которые можно трактовать как переход в нулевую категорию. Общее количество категорий при этом увеличивается на единицу: М = 18.

Значение Pg может в известной мере служить интегральной мерой креативности ответов испытуемого. При этом наблюдается обратная зависимость: чем меньше эта вероятность, тем, в принципе, большей может считаться креативность. Для того чтобы получить прямую зависимость и уменьшить нелинейность оценок, для вычисления интегрального (генерального) показателя креативности удобно использовать логарифмическое преобразование:

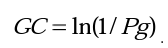
Однако в данном случае эти расчеты не представляют практического интереса в силу наблюдающейся большой неоднородности в беглости ответов испытуемых: распределение испытуемых по беглости носит экспоненциальный характер, и количество испытуемых быстро сокращается с увеличением F В результате для статистически адекватных расчетов необходимы очень большие выборки, что мало осуществимо на практике. Кроме того, значения показателя GC зависят от выборки испытуемых, что затрудняет сравнение результатов разных реализаций теста.

В связи с этим интересно рассмотреть вероятностную модель, в которой неоднородность переходов по графу семантической сети учитывается в качестве отдельного фактора и при этом обеспечивается независимость расчета показателей креативности от выборки испытуемых.

Иниционно-семантическая модель теста эмоциональной креативности. С учетом сделанных выше предположений общую вероятность Pg без введения дополнительной нулевой категории можно представить в виде произведения частных вероятностей: K

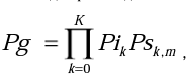
где Pik - вероятность в принципе дать ответ на каждом шаге, Psk,m - условная вероятность перехода в конкретную категорию. Эмпирические оценки этих вероятностей определяются формулами:

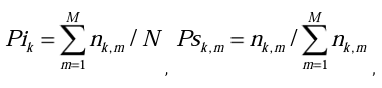
где к - номер шага, m - номер категории, M - число категорий (без нулевой), N - число испытуемых в выборке, nk,m - количество испытуемых, давших ответ в m категории на k шаге.

При этом Pik зависит только от номера шага и не зависит от выбора категории, а Psk,m фактически определяет выбор категории на каждом шаге, если этот шаг имеет место.

Анализ вероятностей Psk, m показывает, что распределения этих вероятностей в выборке для каждого из шагов имеют в принципе близкую форму, т.е. в первом приближении можно не учитывать изменение Ps в зависимости от номера шага k и рассматривать только общее для всех шагов усредненное распределение вероятности Psm. Это распределение может быть определено для большой выборки и затем считаться постоянной характеристической нормой динамики передвижения по семантической сети. Зависимость вероятности Pi от номера шага тоже можно аппроксимировать и затем использовать в нормированных таким образом расчетах креативности.

Предложенная упрощенная вероятностная модель продуцирования категориальных ответов теста математически соответствует ситуации бросания игральной кости с 17-ю гранями и со смещенным центром (т.е. каждая грань соответствует одной категории, и вероятности Psm выпадения каждой из граней разные) в случае, когда вероятность инициации самого броска Pik предсказуемо быстро падает с увеличением k. После определения на основании имеющихся эмпирических данных этих двух типов базовых вероятностей модель позволяет рассчитывать индивидуальные показатели испытуемых единообразным образом независимо от разброса данных в конкретной выборке испытуемых.

Представленную вероятностную модель можно назвать иниционно-семантической моделью, в которой к традиционно рассматриваемому латентному фактору семантической активации памяти и мышления добавляется второй латентный фактор. Можно предположить, что он характеризует именно инициативность испытуемого, которая в результате в значительной мере определяет креативность испытуемых в тестовой ситуации. Процесс выбора ответа в данной категории в модели дополняется процессом инициации этого выбора. Это означает, что в первом приближении продуцирование на каждом шаге теста семантически разных ответов осуществляется вместе с инициацией мыслительных действий (по продуцированию этих категорий), причем эти процессы являются независимыми друг от друга.

Зависимость вероятности инициации броска (выбора категории) от номера шага назовем функцией инициативности Ik. На основании имеющихся экспериментальных данных в первом приближении Ik можно аппроксимировать экспоненциальной функцией, которая зависит только от номера шага k:

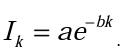
Эта функция определена при k > 0 (при k = 0 полагаем I0 = 1) и задает для каждого испытуемого группу вероятностей перехода Pik, которые быстро уменьшаются с каждым новым переходом. Функция инициативности определяет вероятностный потенциал испытуемого дать в тестовой ситуации следующий ответ. Примерные значения параметров a и b функции Ik могут быть определены с помощью регрессионного анализа (например, в SPSS). Для имеющейся выборки испытуемых/ a = 1,332, b = 0,681.

На основании введенной аппроксимации функции креативности можно вычислить кумулятивный логарифмический показатель иниционной креативности испытуемого как функцию, зависящую от его беглости, K=F:

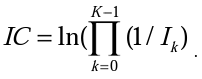
Другая группа вероятностей переходов по семантической сети соответствует вероятностям Pm, каждая из которых показывает средние шансы появления данной категории m из всех M=17 категорий. Эти шансы можно определить как отношение числа реальных выборов каждой из категорий к числу всех ответов всех ответивших испытуемых во всех шагах. Диаграмма, показывающая значения усредненных вероятностей Pm для анализируемой выборки, приведена на рис. 3.

Как видно из диаграммы, разброс вероятностей появления категорий весьма велик. Для ряда категорий (1, 4, 9, 12, 8 и 6) вероятности их появления превышают среднюю вероятность 0,059 выбора одной категории из 17 в случае равновероятного выпадения категорий. Эти категории получают преимущественное распространение в ответах.

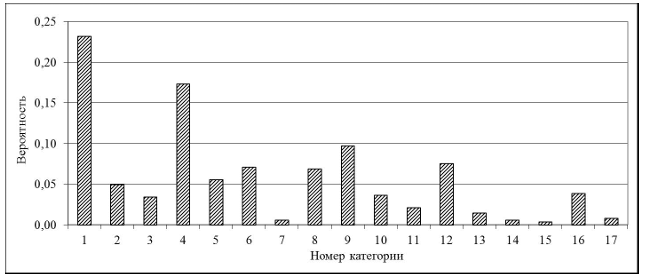
Рис. 3. Усредненное распределение вероятностей появления на каждом шаге любой из 17 категорий теста

На основании найденного распределения, зная категориальную цепь ответов испытуемого, можно оценить семантическую креативность испытуемого:

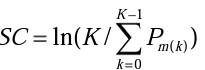
При K = F формула вычисляет среднее значение группы вероятностей Pm и определяет показатель семантической креативности. При K = 1 с помощью этой формулы можно оценить разброс значений SC (от минимума до максимума Pm(k) при изменении k). Средние значения этого показателя и разброс значений SC для 198 испытуемых показаны на рис. 4. Видно, что значительное количество испытуемых имеют значения показателя SC ниже общего среднего значения 2,8, т.е. работают с категориями, имеющими высокую вероятность появления.

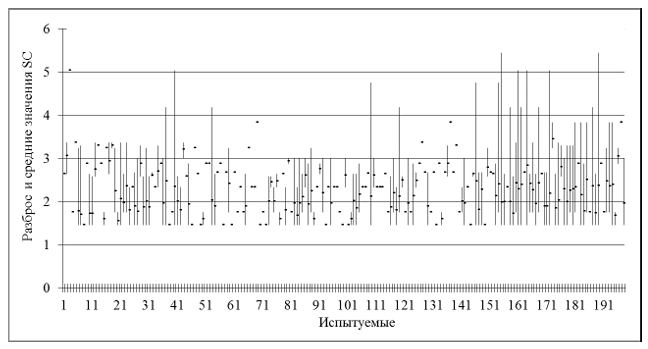
Рис. 4. Распределение средних значений (точки) и разброс значений (вертикальные линии) показателя семантической креативности SC для заданной выборки испытуемых

На рис. 5 представлена диаграмма, показывающая распределение испытуемых в соответствии с их показателями SC и IC.

Практически все значения SC на рис. 5, соответствующие данным после трех первых шагов, находятся ниже общего среднего уровня 2,8. Превышение этого уровня для маленьких значений IC указывает на тот факт, что часть людей с малым IC используют оригинальные категории, и в этом смысле они могут являться не менее креативными, чем люди с большой инициативностью (IC).

Для оценки точности расчетов, сделанных с помощью независимой от выборки иниционно-семантической модели, интересно сравнить рассчитанные для имеющейся выборки значения модельных показателей IC и SC с их значениями, полученными без использования модельных аппроксимаций. Расчет соответствующих коэффициентов корреляций Спирмана R дает следующие результаты: R(IC) = 0,99, R(SC) = 0,91, что свидетельствует в пользу применимости иниционно-семантической модели.

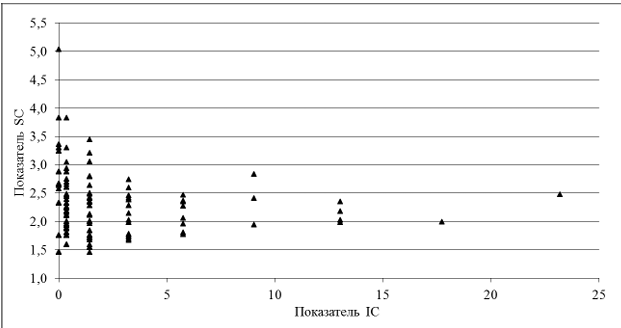
Рис. 5. Распределение испытуемых в зависимости от среднего значения их показателя SC(F) и значения показателя IC

Иниционно-семантическая модель, на наш взгляд, интересна тем, что в ней выделяются две группы независимых вероятностных явлений (относящихся к разным типам активности испытуемого: инициативности и семантической избирательности), характеристики которых можно с достаточной точностью аппроксимировать. Тем самым можно обеспечить относительную независимость конечных расчетов от экспериментальной выборки испытуемых.

Представленная модель дает также возможность рассчитать интегральный показатель креативности, который учитывает как количество ответов, так и их разнообразие и оригинальность:

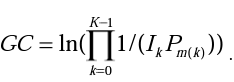
При этом если положить K = F то испытуемые с большой беглостью будут в целом иметь и большие значения GC В целях выравнивания значений интегрального показателя для разных групп испытуемых предлагается использовать общее значение K, а для отсутствующих ответов брать среднее значение Pm(k) = 1/M.

Следует отметить, что нахождение единого коэффициента творческого мышления является насущным вопросом в психологии творчества [6], в этой связи представленный интегральный показатель GC может быть полезным для верификации различных тестов дивергентной креативности.

Основные результаты и выводы. Таким образом, мы построили и представили в графическом виде семантическую сеть, рассчитали ее структурные характеристики (кластеризация и ассортативность) и провели статистический анализ категориальных ответов задания дивергентного теста эмоциональной креативности.

На этой основе мы предложили новую двухфакторную иниционно-семантическую вероятностную модель продуцирования тестовых категорий. Модель позволяет выделить в ситуации дивергентного тестирования два отдельных независимых латентных фактора: инициативность испытуемого и его семантическую избирательность. Психологически фактор инициативности определяется побудительными мотивами к произвольному поведению и связан с различными активационными проблемами, стоящими на пути претворения мыслительных действий и активации памяти. Второй фактор определяется собственно активацией семантических процессов мышления в соответствии с представлениями и предпочтениями испытуемого.

В рамках предложенной вероятностной модели нами были введены новые расчетные тестовые показатели: интегральный показатель креативности, а также независимые друг от друга показатели иниционной креативности (соответствует уровню инициативности испытуемого) и семантической креативности (определяет оригинальность семантики ответов испытуемого). Вероятностные параметры модели формируются на основе усреднения и аппроксимации статистических характеристик эталонной выборки, что обеспечивает единообразное и соотнесенное с нормой вычисление индивидуальных показателей креативности испытуемых.

Развитый нами вероятностный подход к исследованию семантики и категориальной структуры ответов теста эмоциональной креативности является достаточно общим и может быть применен для анализа и оценки результатов других дивергентных тестов креативности и творческого мышления.

Автор выражает благодарность кандидату психологических наук С.С. Беловой за постановку задачи и предоставленные исходные данные.

1. Аверина И.С., Щебланова Е.И. Вербальный тест творческого мышления «Необычное использование». М., 1996.
2. Артеменков С.Л. К расчету характеристических показателей дивергентных тестов креативности // Моделирование и анализ данных. 2011. № 1.
3. Белова С.С. Творчество: психологические и компьютерные модели // Психология. 2008. Том 5. №4.
4. Белова С.С. Творчество с позиций когнитивных сетевых моделей // Одаренный ребенок. 2006. № 6.
5. Белова С.С. Эмоциональная креативность и активационная парадигма в исследовании творчества // Психология человека в современном мире: Материалы Всероссийской юбилейной научной конференции, посвященной 120-летию со дня рождения С.Л. Рубинштейна: В 2 т. Т. 2. М., 2009.
6. Чернецкая Н.И. Эмпирическое моделирование интегрального показателя творческого мышления // Вестник БГТУ им. В.Г.Шухова. 2011. № 3.
7. Bossomaier T., Harre M., Knittel A., Snyder A.A. Semantic network approach to the creativity quotient (CQ) // Creativity Research Journal. 2009. 21(1).
8. Guilford J.P. The Nature of Human Intelligence. N.Y., 1967.
9. Newman M.E.J. The structure and function of complex networks // SIAM Review 45, 167-256 (2003).
10. Torrance E.P. The nature of creativity as manifest in its testing // R.J. Sternberg (ed).. The Nature of Creativity. N.Y., 1988.