Роль модельного эксперимента и фрактального анализа данных в психологическом исследовании

Показана роль модельного эксперимента для повышения объективности оценки теории. Обосновывается, что построение модели процесса на основе оцениваемой теории, проведение компьютерного модельного эксперимента, и сопоставления данных модельного эксперимента с реальными данными по неочевидной характеристике позволяет повысить объективность оценки адекватности теории. В качестве примера такой характеристики использована степень фрактальности последовательности интервалов между действиями.

Введение

По мере формирования новой теории происходит уточнение ее терминологического аппарата, теоретические положения приобретают более строгую форму, что в итоге позволяет провести формализацию теории и построить математическую модель исследуемого процесса на основе этой теории. Наличие математической модели говорит о высоком уровне развития теории, о ее высоком уровне детализации, конкретизации. Для таких развитых научных направлений полный цикл исследования приобретает вид: проведение натурного эксперимента в соответствии с выдвинутой исследовательской гипотезой, модификация теории в связи с полученными результатами, модификация модели с учетом новых теоретических положений, проведение компьютерного модельного эксперимента с целью тестирования теории на полноту и непротиворечивость, генерация новой исследовательской гипотезы на основе модельного эксперимента (рисунок 1).

Проведение компьютерного эксперимента с моделью позволяет проверить полноту теории и ее внутреннюю непротиворечивость. Теория, как набор теоретических положений, представляет собой совокупность представлений об исследуемом процессе (предмете исследования). Моделирование позволяет воплотить эти представления в модельном виде и затем путем проведением компьютерного эксперимента сопоставить модельный процесс с реальным. Таким способом исследователь может увидеть, каким был бы реальный процесс, если бы его представления о процессе были верны.

Введение

По мере формирования новой теории происходит уточнение ее терминологического аппарата, теоретические положения приобретают более строгую форму, что в итоге позволяет провести формализацию теории и построить математическую модель исследуемого процесса на основе этой теории. Наличие математической модели говорит о высоком уровне развития теории, о ее высоком уровне детализации, конкретизации. Для таких развитых научных направлений полный цикл исследования приобретает вид: проведение натурного эксперимента в соответствии с выдвинутой исследовательской гипотезой, модификация теории в связи с полученными результатами, модификация модели с учетом новых теоретических положений, проведение компьютерного модельного эксперимента с целью тестирования теории на полноту и непротиворечивость, генерация новой исследовательской гипотезы на основе модельного эксперимента (рисунок 1).

Проведение компьютерного эксперимента с моделью позволяет проверить полноту теории и ее внутреннюю непротиворечивость. Теория, как набор теоретических положений, представляет собой совокупность представлений об исследуемом процессе (предмете исследования). Моделирование позволяет воплотить эти представления в модельном виде и затем путем проведением компьютерного эксперимента сопоставить модельный процесс с реальным. Таким способом исследователь может увидеть, каким был бы реальный процесс, если бы его представления о процессе были верны.

Рис. 1. Цикл экспериментального исследования. Наверху – петля без модельного эксперимента: теория формулирует гипотезу экспериментального исследования, трактует полученные данные и модифицирует себя, что отражает субъективизм при верификации теорией самой себя. Внизу – петля с модельным экспериментом: данные, полученные на основе компьютерного эксперимента с моделью, напрямую сопоставляются с данными натурного эксперимента

Для объективной проверки теории существует натурный эксперимент, но насколько он объективен как метод верификации теории? При проверке теории натурным экспериментом исследователь строит гипотезу исследования на основе именно проверяемой теории и трактует полученные данные на основе опять же проверяемой теории. Это создает субъективность проверки теории: получается, что теория проверяет сама себя, через призму себя, глядя на реальность. При обнаружении «аномалий» путем натурного эксперимента, т.е. при обнаружении данных, противоречащих теории, на следующем шаге цикла принято дорабатывать теорию, а не отвергать ее. В итоге теория не может отвергнуть сама себя, она сохраняет свое «твердое ядро» и лишь модифицирует «защитный пояс» (Лакатос, 1995).

При дополнительной проверке теории с помощью модельного эксперимента мы получаем возможность усилить объективность оценки теории, поскольку теперь не трактуем данные с помощью теории, а напрямую сопоставляем данные, полученные в натурном и модельном экспериментах (рисунок 1, внизу). Для этого будем использовать такие данные, которые эксплицитно в теории не фигурируют.

Например, теория рефлекса является достаточно развитой теорией и позволяет провести ее формализацию и построить математическую модель (Крылов, Александров, 2008). Мы создали компьютерную математическую модель рефлекторного агента, т. е. создали искусственного агента, который вел себя так, как предполагает теория рефлекса. Проведение компьютерного эксперимента позволило нам обнаружить, какое поведение можно было бы ожидать от реальных животных, если бы они были рефлекторны, т.е. если бы теория рефлекса была бы верна (Крылов, Александров, 2007, 2008, 2009). Зарегистрированные в компьютерном эксперименте поведенческие феномены являются следствием теории, и, если они не совпадут с поведением животных, значит, теория в чем-то неверна. Теория рефлекса оперирует связью между текущей ситуацией S(t) и последующим действием A(t) (что и называется «рефлекс»), но не делает никаких эксплицитных утверждений относительно связи между текущим действием A(t) и последующей ситуацией S(t+1) и не предполагает изменения распределения статистики возникновения различных ситуаций в процессе обучения. Именно эти величины были использованы нами для анализа теории рефлекса, и получены они были путем компьютерного эксперимента с моделью рефлекторного агента (Крылов, Александров, 2007, 2008, 2009). Результаты показали, что рефлекторный агент при взаимодействии со средой демонстрирует такие свойства, которые рефлекторной теорией не могут быть адекватно описаны. Это означает, что рефлекторная теория неадекватна для описания взаимодействия организма со средой.

Далее представлен пример применения такого подхода к анализу цепочек действий.

Процедура и методы исследования

Рассмотрим некоторое поведение, в котором у испытуемого есть выбор только из двух альтернативных действий – «А» и «Б». Это могут быть эксперименты по распознаванию сигнала, в которых испытуемый должен принимать одно из двух решений относительно текущего стимула, или эксперименты, в которых животное движется направо («А») или налево («Б»), или данные регистрации нейронной активности, в которых в каждый момент времени спайк либо есть («Б»), либо его нет («А»). Известно, что животные в такого рода задачах демонстрируют поведение, обладающее фрактальной структурой, которое обнаруживается с помощью гистограмм интервалов в логарифмических осях (Непомнящих, 2003). Также последовательность межспайковых интервалов активности нейронов демонстрирует наличие фрактальной структуры, которую можно выявить, вычислив фактор Аллана (Teich, 1997).

Пусть в имеющихся данных, полученных в натурном эксперименте, в 94% случаев выполнялось действие «А» и в 6 % случаев выполнялось действие «Б». На основе рефлекторного подхода можем сформулировать такую частную теорию применительно к нашим данным: «Есть рефлекс совершать действие «А», и он выполняется в 94 % случаев, и есть рефлекс совершать «Б», и он выполняется в 6 % случаев». Эта теория не делает никаких эксплицитных утверждений относительно того, сколько раз подряд может выбираться «А», т.е. о длительностях времени между совершениями действия «Б». Именно эту характеристику будем определять путем проведения модельного компьютерного эксперимента и сопоставлять с аналогичными данными натурного эксперимента. Если проводить упомянутую аналогию с нейронной активностью, то речь идет о межспайковых интервалах. Построим модель на основе этой теории и в компьютерном эксперименте с ней получим последовательность временных интервалов между действиями «Б», отражающую сегменты непрерывного совершения действия «А». Так определим, каким был бы реальный процесс, если бы эта гипотетическая теория была верна. Полученные данные, предсказанные теорией, сопоставим с данными натурного эксперимента.

Для оценки скрытых закономерностей в последовательности действий будем использовать показатель фрактальности этой последовательности. Для этого данные представим в виде гистограммы интервалов в логарифмических осях, проведем линейную аппроксимацию кривых (Непомнящих, 2003) и сопоставим модельную кривую с экспериментальной визуально. Более строгое сопоставление данных предсказываемых теорией и натурных проведем, вычисляя фактор Аллана, оценивающий наличие фрактальной структуры в последовательности действий (Teich, 1997).

Результаты исследования

Рис. 2. Гистограммы интервалов между совершениями действия «Б» в логарифмических осях, с логарифмической величиной бина и нормализацией к величине бина

Результаты расчетов по модели и по натурным данным представлены на рисунке 2. Видно, что результаты обработки модельных данных отличаются от натурных данных. Это означает, что теория неадекватно описывает имеющиеся данные, несмотря на то что построена на основе этих данных.

Однако являются ли эти отличия качественными или всего лишь количественными? Можно думать, что отличия между модельными результатами и натурными данными являются только количественными, и если подобрать подходящие численные параметры модели (коэффициенты), то можно получить удовлетворительное соответствие данным. В этом случае наша гипотетическая теория смогла бы «спасти» себя. Например, данные, предсказанные теорией для интервалов величины 2–35, т.е. большая часть данных, аппроксимируются прямой линией с углом наклона 0,83, а реальные данные аппроксимируются прямой линией с углом наклона 2,15. Можно было бы думать, что возможность аппроксимации прямой линией означает качественное сходство реальных и теоретически предсказанных интервалов, а разный угол наклона отражает лишь непринципиальные количественные различия. Можно было бы сделать вывод, что теория качественно адекватно описывает большую часть данных.

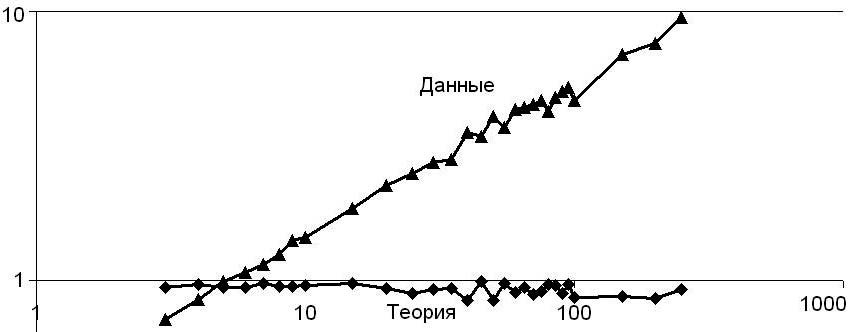
Рис. 3. Фактор Аллана для данных, предсказанных теорией («Теория») и для реальных данных («Данные»). Теория предсказывает, что данные должны иметь фактор Алана, близкий к 1, что означает отсутствие фрактальности в них. Реальные данные демонстрируют линейный рост фактора Аллана в логарифмическом масштабе, что доказывает наличие фрактальной структуры в них

Однако проведем анализ последовательности интервалов с оценкой фрактальности. Чтобы оценить соответствие теоретически предсказанных данных с натурными данными качественно, мы рассчитали фактор Аллана. Он представлен на рисунке 3. Если процесс является случайным процессом пуассоновского типа, без фрактальности, то фактор Аллана равен 1. Если процесс имеет фрактальную природу, то фактор Аллана линейно растет в логарифмических координатах (Teich, 1997).

По рисунку 3 видно, что теория описывает нефрактальный процесс, подобный пуассоновскому, в то время как реальный процесс имеет фрактальную структуру (линейный рост фактора Аллана). Следовательно, наша гипотетическая теория не только количественно, но и качественно непригодна для описания данного процесса, и ее следует отвергнуть.

Заключение

Продемонстрирован подход для оценки адекватности теорий путем формализации теории, построения модели процесса на основе оцениваемой теории, проведения компьютерного модельного эксперимента и сопоставления данных модельного эксперимента с реальными данными. Такой подход позволяет усилить адекватность в оценке теорий по сравнению с классическим подходом проверки теорией самой себя и последующей самомодификации теории. В качестве сопоставляемой характеристики данных предложено использовать такую, о которой теория не делает эксплицитных утверждений и которая является нелинейным (неочевидным, эмерджентным) следствием из постулатов теории. В настоящей работе в качестве такой характеристики использовалась оценка фрактальности последовательности интервалов между разнотипными действиями.

1. Крылов А.К., Александров Ю.И. Погружение в среду как альтернатива методике предъявления стимулов: модельное исследование // Психологический журнал. 2007. Т. 28. № 2. С.106–113.
2. Крылов А.К., Александров Ю.И. Парадигма активности: от методологии эксперимента к системному описанию сознания и культуры // Компьютеры, мозг, познание: успехи когнитивных наук / Отв. ред. Б. М. Величковский, В. Д. Соловьев. М.: Наука, 2008. С. 133–160.
3. Крылов А.К., Александров Ю.И. Особенности взаимодействия рефлекторного агента со средой: модельное исследование // Экспериментальная психология. 2009. № 1. С. 5–22.
4. Лакатос И. Фальсификация и методология научно-исследовательских программ. М.: Медиум, 1995.
5. Непомнящих В. А. Как животные решают плохо формализуемые задачи // Проблемы интеллектуального управления – общесистемные, эволюционные и нейросетевые аспекты // Нейроинформатика-2003. М.: МИФИ, 2003. С. 186–190.
6. Teich M. C., Heneghan C., Lowen S. B., Ozaki Y., Kaplan E. Fractal Character of the Neural Spike Train in the Visual System of the Cat // J. Opt. Soc. Am. A. V. 14. 1997. Р. 529–546.