Построение шкалы отношений на основе данных прямых методов оценки стимулов, не имеющих физической метрики

Теоретическая модель построения шкалы отношений

В психологии до сих пор право построения шкал отношений на основе результатов прямых методов измерений традиционно оставляется психофизике-2 Стивенса, несмотря на то, что Г. Экман еще в 50-е годы прошлого века использовал методы непосредственной оценки отношений, в которых испытуемый не имел возможности изменять «интенсивность» стимула, как, например, в методе бисекции Стивенса (Экман, Кюннапс, 1972; Экман, 1959).

Если прямые категориальные оценки (оценки интервалов) достаточно часто применяются при психологических измерениях, то прямые оценки отношений менее популярны, особенно в психометрических задачах при невозможности измерить стимулы в физической шкале.

Мы постараемся показать способность человека адекватно манипулировать образами стимулов в структуре «обобщенного образа» на уровне оценки отношений, т. е. доказать возможность построения психологической шкалы отношений на основе данных прямых методов оценки (Худяков, 2000).

Теоретическая модель построения шкалы отношений

В психологии до сих пор право построения шкал отношений на основе результатов прямых методов измерений традиционно оставляется психофизике-2 Стивенса, несмотря на то, что Г. Экман еще в 50-е годы прошлого века использовал методы непосредственной оценки отношений, в которых испытуемый не имел возможности изменять «интенсивность» стимула, как, например, в методе бисекции Стивенса (Экман, Кюннапс, 1972; Экман, 1959).

Если прямые категориальные оценки (оценки интервалов) достаточно часто применяются при психологических измерениях, то прямые оценки отношений менее популярны, особенно в психометрических задачах при невозможности измерить стимулы в физической шкале.

Мы постараемся показать способность человека адекватно манипулировать образами стимулов в структуре «обобщенного образа» на уровне оценки отношений, т. е. доказать возможность построения психологической шкалы отношений на основе данных прямых методов оценки (Худяков, 2000).

В основе построения искомой шкалы лежит экспериментально полученная матрица парных сравнений, в которой каждый элемент представляет оценку отношения степени выраженности указанного критерия в двух сравниваемых стимулах. Т. е. испытуемый должен указать во сколько раз один стимул в паре больше отвечает предложенному критерию оценки по сравнению с другим. aij = Si/ Sj (1), где aij – элемент матрицы парных сравнений, представляющий оценку отношения между соответствующими стимулами (i – номер столбца матрицы, j – номер строки); Si , Sj – числовые представления стимулов в субъективном пространстве, т. е. искомые шкальные значения.

В результате проведения эмпирической процедуры измерения (эксперимента) мы получаем неполную матрицу парных сравнений отношений. В этой матрице номер столбца каждой заполненной клеточки соответствует номеру стимула, который был в паре оценен выше, следовательно, число, стоящее в этой ячейке, больше 1. Диагональные элементы матрицы представлены 1, так как они отвечают случаю сравнения стимула с самим собой. Поэтому на первом шаге обработки экспериментальная неполная матрица преобразовывается в полную, т. е. в симметричную незаполненную ячейку помещается величина обратная величине в соответствующей заполненной ячейки: aij = 1/aji .

Проведем суммирование равенства (1) по индексу i: Σiaij = (ΣiSi )(1/Sj ), т. е. суммирование элементов матрицы в j-й строке. Из этого равенства следует Sj = ΣiSi /Σiaij . ΣSi – для данного набора стимулов и конкретного испытуемого является константой. Обозначим ее k1 , ΣiSi = k1 . Шкала отношений, по определению, задается с точностью до произвольной константы «а», определяющей масштаб или единицу измерения шкалы: y = ax – допустимое преобразование. Так как мы предполагаем построение шкалы отношений, то здесь и далее нам вполне достаточно получить шкальные значения с точностью до некоторой произвольной константы, значение которой мы можем считать равным 1.

Таким образом, мы получаем искомое шкальное значение для j-того стимула: Sj = k1 /Σiaij или Sj = 1/Σiaij (2).

Проведем суммирование равенства (1) по индексу j, т. е. суммирование в i-м столбце Σjaij = Si Σj(1/Sj ). Σj(1/Sj ) – величина постоянная для данного набора стимулов и данного испытуемого, следовательно, Σj(1/Sj) = k2 . Мы получаем искомое шкальное значение для i-го стимула: Si = k2 Σjaij или Si = Σjaij (3).

Рассмотрим случай i = j = y: Sj = Si = Sy = k1 /Σiaiy = k2 Σjayj, из этого следует (Sy Sy ) = (k1 k2 )(Σjayj /Σiaiy ).

С точностью до константы (k1 k2 ), мы получили третье выражение для искомого шкального значения: Sy = √(Σjayj /Σiaiy ) (4).

Кроме этого, из приведенных рассуждений следует наличие еще одной константы, значение которой может быть оценено в эксперименте, а именно, из равенства k1 /Σiaiy = k2 Σjayj следует Σiaiy Σjayj = k1/ k2 (5), т. е. для данного набора стимулов и данного испытуемого (для конкретной экспериментально полученной полной матрицы парных сравнений отношений) должно быть постоянным произведение сумм элементов матрицы по строкам и по столбцам, в случае выполнения наших предположений. А предположение, положенное в основу приведенных рассуждений, было одно: испытуемый в состоянии адекватно оценивать отношение субъективных значений пары стимулов.

Найденные шкальные значения Si представляют индивидуальную шкалу отношений конкретного испытуемого. Если эта шкала действительно обладает свойствами шкалы отношений, то шкальное значение индивидуальной шкалы Si связано с «истинным» значением Ri линейным соотношением bRi . Si = bRi , следовательно, ΣSi = bΣRi , отсюда b = ΣSi /ΣRi . Ri = Si /ΣSi (6), так как значение суммы ΣRi является постоянным для данного стимульного набора, точнее для представления данного стимульного набора в совокупном обобщенном образе.

«Совокупный обобщенный образ» – рабочее название обобщенного образа группы испытуемых однородной по реакции на предложенный стимульный набор (Худяков, 2000).

Правильность вышеприведенных выводов и предлагаемого алгоритм построения шкалы отношений проверяется экспериментально.

Доказательством возможности построения шкалы отношений прямыми методами оценки может служить два факта: 1) выполнение равенства (5) Σiaiy Σjayj = k для полученной в эксперименте матрицы; 2) три построенные на этой матрице шкалы – Sj = k1 /Σiaij , Si = k2 Σjaij , Sy = √(Σjayj /Σiaiy ) – должны быть эквивалентны с точностью до постоянного множителя, т. е. связаны соотношением y = ax.

Описание эксперимента

Стимульный набор

Стимульный набор состоял из 20 фотографий, сделанных фотохудожником Ю. В. Ермоловым. В наборе представлено 4 различных сюжета – один человек или группа людей в бытовой обстановке. Каждому сюжету соответствует 5 фотоизображений, которые отличаются степенью контраста. Отличия степени контраста фотоизображений в пределах каждого сюжета одинаковы для всех 4 сюжетов. Использование фотографий реальных сюжетов, а не схематических изображений повышало экологическую валидность эксперимента.

Испытуемые

В эксперименте приняли участие 43 человека – студенты третьего курса факультета психологии СПбГУ.

Процедура

Испытуемым в случайном порядке предъявлялись пары стимулов из набора. В качестве критерия оценки был выбран интегральный критерий «простое предпочтение».

Предлагалась инструкция: «Вам будут предъявляться пары фотографий. Ваша задача выбрать ту фотографию в паре, которая кажется вам более предпочтительной в предложенной паре. Кроме того, оцените, пожалуйста, во сколько раз вам показалась предпочтительней выбранная вами фотография по отношению ко второй фотографии в паре».

Ответы испытуемых заносились в матрицу парных сравнений. Далее метод непосредственной оценки отношений будем называть НОО.

По данным метода НОО строились предполагаемые шкалы отношений по описанным в уравнениях (2), (3), (4) алгоритмам с нормированием на сумму шкальных оценок согласно уравнению (6) (НОО-2, НОО-3, НОО-4). Кроме того, вычислялись значение константы – уравнение (5) (НОО-1).

По результатам метода парных сравнений (МПС) без учета оценки отношений была построена шкала, шкальные значения которой вычислялись как усредненные по выборке испытуемых суммы предпочтений, полученных каждым стимулом. Ранее нами было показано, что такая шкала является шкалой интервалов (Гусев, Зароченцев, 1988; Зароченцев, Оганян, 1988).

Анализ результатов

На первом шаге проверки рассмотрим, насколько в полученных экспериментальных данных выполняется равенство (5).

Распределение этих оценок имеет следующие характеристики: среднее значение – 58,25, оценка среднеквадратичного отклонения – 1,7, размах max – min = (61,2 – 55,3) = 5,9. Можно сделать вывод, что соотношение (5) вполне выполняется, а флуктуации этой «константы» вызваны погрешностями измерения.

На втором шаге проверялась гипотеза о линейном характере связи между шкалами, построенными согласно уравнениям (2), (3), (4) (НОО-2, НОО-3, НОО-4). Значения соответствующих статистик, приведенные в таблице 1, не дают оснований отклонить гипотезу о линейной связи между построенными шкалами.

Далее мы проверили вид связи между шкалой, построенной на основе данных МПС, которая является, как минимум, шкалой интервалов (Гусев, Зароченцев, 1988; Зароченцев, Оганян, 1988), и шкалами, построенными по данным непосредственной оценки отношений. Регрессионный анализ и в этом случае не отклоняет гипотезу о линейной зависимости. В таблице 2 приведены результаты регрессионного анализа. Рисунки 1 и 2 иллюстрируют эти зависимости. При построении этих графиков, соответствующие шкальные значения были смещены к общей нулевой точке.

Таблица 1 Оценка линейности связи между шкалами, построенными на основе результатов методов НОО-2, НОО-3, НОО-4

Примечания: F1 , F2 – статистики Фишера для оценки адекватности линейной модели; F3 – статистика Фишера для оценки корректности линейной модели; r – значение коэффициента корреляции.

Таблица 2 Оценка линейности связи между шкалами, построенными на основе результатов методов НОО-2, НОО-3, НОО-4 и МПС

Примечания: F1 , F2 – статистики Фишера для оценки адекватности линейной модели; F3 – статистика Фишера для оценки корректности линейной модели; r – значение коэффициента корреляции.

Примечания к таблице данных проверки линейности связей

Проверяется линейная модель y = ax + b + e; а, b – параметры модели, e – случайное отклонение.

1) Проверка адекватности модели

Для этого была использована схема, в которой x и y не случайны, но могут быть измерены с некоторыми случайными ошибками, главное, чтобы ошибки были меньше диапазона изменений переменных (Айвазян, Енюков, Метелкин, 1985). Исходная модель удовлетворяет требованиям этой схемы. F1 = (m – 1)(1 – r2 )Sy 2 /[(m – 2)ΣSyi 2 ], F2 = nF1 m – количество точек, Syi – оценки соответствующих среднеквадратичных отклонений в точках i, r – коэффициент корреляции между x и y, n – количество измерений в точке i, Sy – оценка среднеквадратичного отклонения переменной y.

Если F1 >1, F2 >F0 , гипотеза о линейной зависимости отвергается.

2) Проверка значимости регрессии (корректности линейной модели)

F3 = (m – 2)r2 /(1 – r2 ). Если F3<F0, гипотеза о корректности модели отвергается. F0 = 6,6 для уровня значимости 0,05.

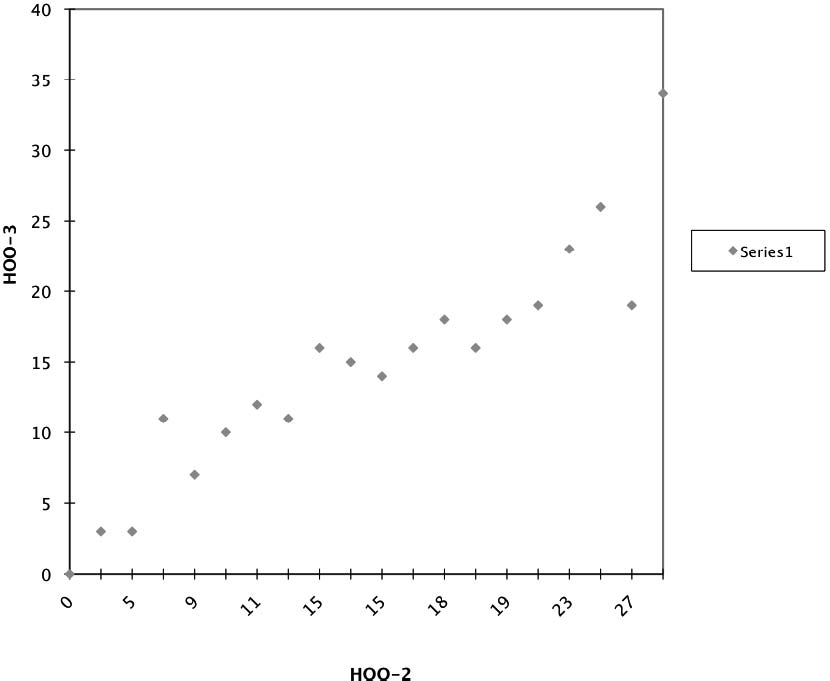
Рис. 1. Связь между шкалами НОО-2 и НОО-3

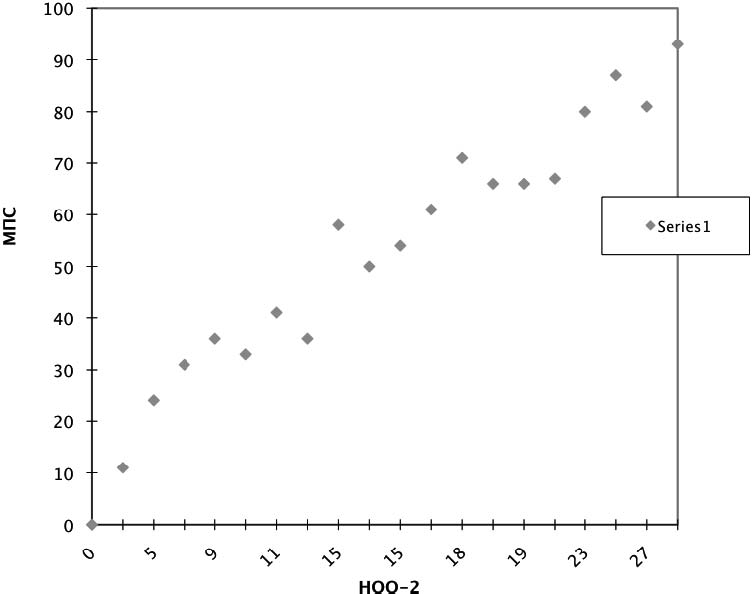
Рис. 2. Связь между шкалами, построенными по данным методов НОО и МПС

Таким образом, анализ экспериментальных данных подтверждает выдвинутые предположения, положенные в основу построения шкал отношений: постоянство произведения сумм по строкам и по столбцам и эквивалентность трех построенных шкал. Это подкрепляется линейностью связи со шкалой, построенной по данным МПС. Следовательно, можно сделать вывод, что построенные шкалы действительно являются шкалами отношений, что испытуемый в состоянии адекватно непосредственно оценивать отношения между образами стимулов.

1. Айвазян С. А., Енюков И. С., Метелкин Л. Д. Прикладная статистика: исследование зависимостей. М., 1985.
2. Гусев Е. К., Зароченцев К. Д. Опыт построения метрической психологической шкалы // Психолого-педагогическое обеспечение учебного процесса в высшей школе в условиях ее перестройки. Л.–М., 1988. С. 308–315.
3. Зароченцев К.Д., Оганян Н.В. Психологическое метрическое шкалирование и экспертные оценки в любительской фотографии // Труды ГОИ им. С. И. Вавилова, 1988. Т. 70. Вып. 204. С. 114–119.
4. Худяков А. И., Зароченцев К. Д. Обобщенный образ как предмет психофизики. СПб.: Изд. СПбГУ, 2000.
5. Экман Г., Кюннапс Т. Шкалирование эстетических оценок «прямыми» и «косвенными» методами // Семиотика и искусствометрия. М., 1972. С. 264, 267–277.
6. Ekman G. Weber’s low and related functions // Journal of Psychology. 1959. № 47. Р. 343–352.