Экспериментальное исследование принятия решения в ситуации неантагонистического взаимодействия двух лиц

Представлен метод описания принятия решений в конфликтной ситуации. Построена нормативная математическая модель принятие решений, учитывающая различия в критериях выбора индивидуальных стратегий поведения субъекта. Разработан и проведен эксперимент по проверке данной модели. Выявлены типы поведения в диадном взаимодействии, уточняющие типы, выявляемые методикой Томаса.

Понятие конфликта широко используется в различных сферах социальной жизни, но часто понимание его не является однозначным. Одно из направлений исследования конфликтов использует в качестве аппарата описания математическую теорию игр. Это связано с тем, что теория игр является цельным математическим аппаратом, обладающим прогностической способностью, а также, что представление социальных взаимодействий в виде матриц возможных исходов является удобным инструментом для описания различных типов социального взаимодействия.

Наиболее интересные результаты в теории игр получены либо для двух лиц с нулевой суммой (теорема Неймана о существовании пары оптимальных смешанных для произвольной матрицы игры), либо для случая бескоалиционных игр многих лиц (теорема Нэша о существовании хотя бы одной точки равновесия в произвольной бескоалиционной конечной игре многих лиц) (Нейман, Моргенштерн, 1970). Однако применение минимаксного критерия, предложенного Дж. фон Нейманом, оказалось малопродуктивным для описания поведения субъектов в реальных конфликтных ситуациях, так как в реальности часто не используются оптимальные стратегии поведения и даже в ситуации неопределенности люди, принимая решение, делают различные предположения о поведение партнера.

В данной работе экспериментально проанализировано поведение игроков в неантагонистической игре с целью построения адекватной математической модели такого поведения (Савченко, 1987). Основное отличие от предыдущих моделей – это учет рефлексии участников игры и их неоптимального поведения с точки зрения теории игр (Савченко, 2002).

Понятие конфликта широко используется в различных сферах социальной жизни, но часто понимание его не является однозначным. Одно из направлений исследования конфликтов использует в качестве аппарата описания математическую теорию игр. Это связано с тем, что теория игр является цельным математическим аппаратом, обладающим прогностической способностью, а также, что представление социальных взаимодействий в виде матриц возможных исходов является удобным инструментом для описания различных типов социального взаимодействия.

Наиболее интересные результаты в теории игр получены либо для двух лиц с нулевой суммой (теорема Неймана о существовании пары оптимальных смешанных для произвольной матрицы игры), либо для случая бескоалиционных игр многих лиц (теорема Нэша о существовании хотя бы одной точки равновесия в произвольной бескоалиционной конечной игре многих лиц) (Нейман, Моргенштерн, 1970). Однако применение минимаксного критерия, предложенного Дж. фон Нейманом, оказалось малопродуктивным для описания поведения субъектов в реальных конфликтных ситуациях, так как в реальности часто не используются оптимальные стратегии поведения и даже в ситуации неопределенности люди, принимая решение, делают различные предположения о поведение партнера.

В данной работе экспериментально проанализировано поведение игроков в неантагонистической игре с целью построения адекватной математической модели такого поведения (Савченко, 1987). Основное отличие от предыдущих моделей – это учет рефлексии участников игры и их неоптимального поведения с точки зрения теории игр (Савченко, 2002).

В данной работе понятие «игра», используемое в теории игр, аналогично понятию «ситуация взаимодействия», а «игра с непротивоположными интересами» – понятию «ситуация взаимодействия с неопределенностью».

Пусть игра двух лиц с ненулевой суммой (биматричная тира) задана при помощи двух матриц: A = ||aij|| и B = ||bij||, где i= 1, 2, …, т; j = 1, 2, …, n. Обозначим через α= (α1, …, α m), β= (β1, …, β n) векторы смешанных стратегий соответственно 1-го и 2-го игроков.

Обозначим через m1= (α, β) и m2= (α, β) математические ожидания выигрыша 1-го и 2-го игроков, если они применяют свои смешанные стратегии α и β соответственно. Каждый игрок, выбирая свою смешанную стратегию, влияет на выигрыши, которые получают оба игрока.

Дж. фон Нейман доказал для игры двух лиц с ненулевой суммой (с непротивоположными интересами) существование таких смешанных стратегий, которые максимизируют гарантированный выигрыш каждого из игроков.

В экспериментах с конкретными играми двух лиц с ненулевой суммой было показано, что игроки применяли различные критерии, часто не соответствующие оптимальной. Например: 1) максимизацию своего выигрыша; 2) минимизацию выигрыша партнера; 3) максимизацию выигрыша партнера; 4) максимизацию суммы выигрышей обоих партнеров; 5) максимизацию разности своего выигрыша и выигрыша партнера и т. д. Все приведенные примеры критериев можно описать в терминах максимизации или минимизации каждым игроком заданной линейной комбинации выигрышей (своего и партнера) с фиксированными (своими: для каж дого игрока) коэффициентами линейной комбинации где i = 1, 2 – номер игрока. Этому и было посвящено проведенное теоретическое исследование.

Т.е. для обоих участников строились функции математических ожиданий выигрышей:

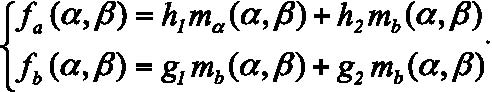
Подставляя коэффициенты h1 h2 для первого игрока, равные 0, 1, –1, будем получать функцию f a, равную математическому ожиданию либо своего выигрыша, либо выигрыша партнера, либо суммарного выигрыша (своего и партнера). Аналогично и для функции g.

Математические ожидания выигрышей являются линейными функциями относительно α и β. Экстремум линейной функции есть геометрическое место точек, лежащих на границе области ее существования.

Нами было предложено следующее определение решения для игры двух лиц с непротивоположными интересами.

Пусть для каждого из игроков, участвующих в игре, определена линейная комбинация выигрышей всех игроков с фиксированными коэффициентами. Критерий (цель, которую стремится достичь данный участник – игрок) определяется как максимизация или минимизация заданной линейной комбинации выигрышей. Игра предполагается бескоалиционной, т.е. каждый игрок выбирает свою стратегию независимо.

Решение игры в данном случае – множество смешанных стратегий всех игроков, которые соответствуют критериям, выбранным каждым из игроков. Естественно, что для заданной игры при некоторых выборах множества критериев игроков решение может существовать, а при других – нет.

В частности, теорема Дж. фон Неймана в этих терминах выглядит следующим образом: если задана игра двух лиц с нулевой суммой, т. е. аij+ bij= 0 (i = 1, 2, …, т; j = 1, 2, …, п), а в качестве критерия каждым из игроков выбрана максимизация своего (гарантированного) выигрыша, то всегда имеется пара смешанных стратегий, удовлетворяющая выбранным критериям (оптимальные стратегии, по Дж. фон Нейману).

В качестве примеров критериев, применяемых каким-либо игроком (например, 1-м в игре двух лиц с ненулевой суммой), могут служить следующие критерии:

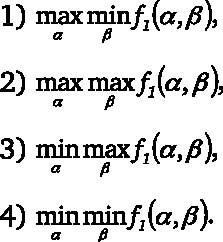
В частности, для игры двух лиц стратегия максимального гарантированно ложенного Дж. фон Нейманом.

Субъект в ситуации конфликта часто не ведет себя по правилам, предложенным нормативной моделью классической теории игр (в некоторый случаях даже и иррационально), а опирается на свои критерии, которые могут быль различными. Ситуация будет приемлемой для обоих участников, если будет существовать решение игры в том смысле как мы его ввели ранее, удовлетворяющее обоих участников.

Т. е. суть метода можно изложить следующим образом: в зависимости от индивидуальных особенностей и ситуации у каждого участника формируется критерий его поведения в предложенной ситуации. Зная критерий и матрицы выигрышей, можно определить, можно ли при таких критериях найти решение из существующего набора, удовлетворяющее критериям обоих игроков и матрицам исходов. Если множества α и β не имеют пересечений, то решение не существует.

Нами была разработана компьютерная программа для построения пространств математических ожиданий для различных матриц выигрышей. Решается система неравенств, находятся области α и β для первого участника, которые определяют решение игры для данной матрицы. Потом аналогичная процедура проводится для второго игрока. Далее находится пространство смешанных стратегий, являющееся пересечением пространств обоих игроков, которое и является решением игры.

Таким образом, предложенная модель позволяет спрогнозировать возможность существования решения игры при заданных критериях и стратегиях поведения участников, т. е. определить, будет ли существовать удовлетворяющее обоих участников разрешение сложившейся ситуации.

Для проверки адекватности модели нами был разработан парный эксперимент. Написана программа для компьютерной коммуникации двух лиц на двух компьютерах. В процессе работы происходил обмен информацией между участниками посредством компьютеров, совершался выбор и получалась информация о своем выигрыше. Участники общались друг с другом посредством компьютеров. Предлагалось два типа игр: с открытой информацией о выигрыше партнера и с закрытой (имелась информация только о своих выигрышах). Участники могли вести переговоры о выборе той или иной стратегии. Перед началом игры участникам предлагалось ознакомиться с легендами игр «семейный спор», «дилемма узника» и др.

Перед испытуемым ставилась задача – набрать как можно больше баллов. Далее предлагалось определить, как будет совершаться действие: совместно с партнером или индивидуально. Кооперативная (совместная) стратегия принималась только в случае выбора ее обоими участниками. При кооперативной стратегии происходили переговоры участников по выбору действий и стратегий поведения. При совпадении предложений совершались ходы, при несовпадении продолжался «торг». При этом фиксировались: протокол «торга», сами ходы, выигрыши за ход и суммарные выигрыши партнеров, время, затраченное на игру.

Так как результат каждого участника зависел и от действий партнера, то создавалась ситуация неопределенности, а в некоторых случаях и конфликтная ситуация. Участник мог провозглашать какую-либо стратегию, а при совершении действия выбирать другую. Также перед началом эксперимента проводилось тестирование участников по методикам К. Томаса и Т. Лири с целью валидизации экспериментального исследования, а после игры участники давали самоотчет в форме свободного интервью.

Данный эксперимент имел многоцелевое назначение.

Одна из задач – это выявление основных типов поведения в диадном взаимодействии и возможности совместной деятельности между ними.

В результате проведенного эксперимента было выявлено несколько типов поведения, что дало хорошее совпадение со способами поведения в конфликтах, выявляемыми методикой К. Томаса.

Однако были и отличия: в методике К. Томаса выделяется всего 5 типов, в нашем экспериментальном исследовании нельзя полностью различить компромисс и сотрудничество, они имеют пересечение, но сотрудничество относится, скорее, к кооперации, т. е. к случаю, когда участники могут договориться друг с другом о выборе каждого хода непосредственно перед совершением действия.

Чтобы определить компромисс, необходимо определить, насколько удовлетворен интерес участника.

В отличие от методики К. Томаса в проведенном эксперименте была выделена более разветвленная структура типов поведения в конфликтной ситуации с учетом рефлексии. Так как в принятом нами ранее определении критерия существует функция, характеризующая предположение о поведении партнера, то каждый тип имел еще разделение по предположению о стремлениях, партнера. Таким образом, в нашем исследовании было выделено 8 типов.

Способы регулирования конфликтов по Томасу и критерии, которые используют игроки, имеют более сложную взаимосвязь.

Рассмотрим более подробно, например, соревнование по Томасу – это стратегия добиться своих интересов в ущерб другому. Мы выделяем в данной ситуации следующие типы, которые имеют более разветвленную структуру:

• компромисс, в предположении о благоприятном настрое партнера;
• компромисс, в предположении о конкурентном поведении партнера;
• приспособление, в предположении, что партнер также увеличивает свой выигрыш;
• приспособление, в предположении о том, что партнер не хочет этого;
• конкуренция также в двух предположениях и т. д.

В нашем исследовании (в отличие от модели дуальных отношений, в которой предполагалось, что отношения к себе и другому – независимы) заложено предположение о влиянии рефлексии о поведении партнера на выбор решения. В методике К. Томаса эту информацию можно получить из заполнения опросника за партнера.

Формально критерии определяются по результатам торга, вычисляются частоты выбора стратегий участниками (реальные ходы). Выявление моментов смены стратегий проводилось по результатам торга, считались частоты предлагаемых игроками стратегий, из которых выбиралась наиболее часто предлагаемая пара.

Данный эксперимент позволил проверить адекватность описанной ранее модели поведения субъекта в обстановке лабораторного эксперимента. Т. е. подтвердить, что действительно испытуемые, ориентирующиеся на какие-либо критерии, выходили на решение, спрогнозированное моделью, либо не находили решение и меняли стратегию или останавливали игру.

Разработанный эксперимент был опробован на двух группах испытуемых: неформально знакомой и неизвестных друг другу респондентах.

Следует заметить, что эксперимент во второй группе является более чистым с точки зрения проверки предложенной модели, так как наличие дополнительных целей усложняет задачу и делает ее неформализуемой с точки зрения теории игр. Однако анализ результатов экспериментов, проведенных с первой группой, дает возможность оценить влияние дополнительных целей на ход переговоров.

Сравнивая две группы игроков между собой, можно заметить, что у знакомой неформально группы игры проходили интереснее, т. е. появлялись дополнительные цели, разнообразящие игры, что, впрочем, является естественным фактом. Во второй группе с увеличением количества сыгранных игр проявлялась тенденция, выявленная Р. Раппопортом и др., к некоторому нивелированию личностных характеристик, т.е. большинство участников выходили на кооперативные стратегии, которые давали максимально гарантированный выигрыш.

Еще одна задача, которая решалась в данном исследовании, – изучение процесса формирования общего решения на основе торга. Как отмечалось выше, перед испытуемыми ставилась задача получения максимального выигрыша, однако часто, особенно в группе знакомых участников, многие помимо главной цели решали и другие задачи.

В ходе эксперимента были также выделены дополнительные цели, которые ставили перед собой участники:

• почувствовать себя лидером, «вести» партнера;
• получение одинаковых выигрышей;
• «научение» партнера на лидера;
• динамика: периодическая смена лидерства партнерами;
• предоставить возможность выиграть партнеру;
• научиться уступать друг другу и др.

Однако наиболее выгодным для обоих участников остается принятие кооперативных решений, несмотря на кажущиеся большие выигрыши, которые можно получить, используя индивидуальные стратегии. Поэтому важно исследовать процесс переговоров и научить участников способам выработки совместных решений.

Таким образом, проведенное экспериментальное исследование позволило верифицировать предложенную теоретико-игровую модель принятия решений в диадном взаимодействии, выделить реально используемые стратегии поведения и соотнести их с оптимальными, провести исследование формирования общей цели на основе индивидуальных, а также сформулировать ряд рекомендаций по построению систем, обучающих ведению переговоров.

1. Нейман фон Дж., Моргенштерн О. Теория игр и экономическое поведение. М., 1970.
2. Савченко Т. Н. Моделирование принятия решений в игре двух лиц с непротивоположными интересами // Психологический журнал. 1987. Т. 8. № 5. С. 142–146.
3. Савченко Т. Н. Развитие математической психологии: история и перспективы // Психологический журнал. 2002. Т. 23. № 5. С. 32–41.