Embodied Cognition in Education: Possibilities and Limitations of Hybrid Representations

The main purpose of this review is to systematize theoretical and experimental research in one of the areas of the field “Embodied Cognition”, aimed at solving applied problems in the field of education, as well as identifying the main opportunities and limitations in using the results obtained. The numerous experimental evidence and new explanatory models that have emerged within the framework of this approach open up a wide range of opportunities for new practices in education. This field offers a whole set of tools that can be used in the pedagogical process in order to increase its purposefulness and effectiveness. We will consider one of the most developed topics – the correlation of abstract concepts in mathematics or disciplines of the natural science spectrum with the specific content of perceptual representations of the student. The approach of embodied cognition allows us to identify the patterns that determine the effectiveness of using various types of visualizations (diagrams, drawings, maps, graphs, diagrams, etc.) in the process of mastering a specific field of knowledge. As a result, the prospects of using the concept of hybrid representations, combining modal perceptual and amodal components, to explain the internal mechanics of the mediation of conceptual thinking are discussed.

Introduction

Currently, there is a large number of theoretical models and empirical facts indicating the important role of the body's sensorimotor activity in the functioning of cognitive processes (for more details, see: [1; 2; 3]). The approach most commonly known as Embodied Cognition has taken its rightful place in the field of fundamental research. Now, its proponents are trying to answer the legitimate question of how to practically apply the results obtained. One of the intriguing areas of application would be education, where problems often arise when students to to master abstract material. This problem is especially common in STEM (Science, technology, engineering, and mathematics) education. It seems likely that the resources provided by the embodied cognition framework are the most efficient and effective for overcoming such difficulties.

Among research in the field of embodied cognition, the most developed framework is “Grounded Cognition”. On the one hand, this is due to the large number of heuristic experimental methods proposed (e.g., the switching cost or feature verification paradigms). On the other hand, it is theoretically the least radical among all the varieties of embodied cognition frameworks, and is much easier to compare with theories and facts derived from more mainstream cognitive research. That is why we will be focusing mostly on grounded cognition paradigms in this review. The main purpose of this review is to systematize the theoretical and experimental studies in the applied field of STEM-education carried out within this framework, as well as to identify the main limitations and opportunities presented by the results obtained. 

One of the most heuristically valuable ideas in the grounded cognition framework regards the fundamental feature of mental representations, that they do not have to be symbolic and amodal. The metaphor of the computer suggests that we receive information through our perceptual system in a modal-specific way (visual, auditory, tactile, etc.) and then translate it into an abstract symbolic amodal format arranged like machine code. One of the founders of the grounded cognition approach, Lawrence Barsalou, pointed out the scarceness of empirical evidence for such a translation. He proposed the alternative scenario that people do not translate one representation into another, but can use modal-specific representations, enacting both perceptual and motor systems, in the process of processing information of any depth and complexity [4]. The computer metaphor does not allow for such a move, considering it meaningless, because the notion that the input and output systems (e.g., keyboard, computer display, etc.) are functionally involved in the operation of the central processor would be absurd. The embodied approach, on the other hand, attempts to combine these two seemingly irreconcilable positions. Its proponents propose the idea that mental representations are associated with both sensorimotor processes and amodal ones. Thus, such representations are hybrid, that is, they contain both multimodal and abstract symbolic components. This position is based on the following arguments:

1)         The classical theories of amodal representationalism assume a rather narrow view of the very nature of mental representations. The research based on such a notion often substitutes “knowing something” as simple verbal “name giving” [5], which is clearly not sufficient.

2)         Conceptual representations are limited by context [6; 7; 8], which does not at all correspond to the amodal point of view.

3)         The neuronal recycling hypothesis [9] argues that if abstract conceptual representations  grounded in perceptual and motor systems, then the answer to the question of how such complex high-level abstract processes (e.g., natural language, mathematics, etc.) could arise and develop in a very short time, relative to an evolutionary timescale.

Hybrid representations offer diverse opportunities for improving the efficiency of the learning process, but they are also associated with significant limitations. We will try to demonstrate these in the material of two rapidly developing areas of research – the understanding of symbolic expressions and of graphs and diagrams.

In both cases, we can find modern research with certain echoes of the cultural-historical theory of Lev Vygotsky. It seems to us that the cited works can be interpreted as quite convincing conceptualizations of the principle of mediation, i.e., the use of diverse cultural means to enhance structurally simpler, and genetically earlier, mental functions [10].

Understanding Symbolic Expressions

The groundedness of abstract mental representations in the perceptual system could be most easily demonstrated within the field of mathematics, the field of knowledge with the most abstract content. As an example, consider how people read and understand symbolic expressions such as algebraic equations. An algebraic equation can describe a huge class of specific situations, so its abstractness is undeniable. Moreover, the meaning of an algebraic equation, of course, does not depend on what color or what font it is printed in. However, the perceptual system makes a significant functional contribution to the understanding of this class of symbolic expressions.

An algebraic equation contains abstract and hierarchically ordered relationships between variables, but the form of the equation is closely related to perceptual characteristics which can also be represented and affect the way the equation will be understood. For example, the spatial proximity between variables may be related to the order in which arithmetic operations are performed. The order in which arithmetic operations are performed determines their hierarchy (high-level operators are executed before low-level ones). Addition requires the variables and operator to be written in full (p + q), while multiplication accepts the shortened version (pq). Both of these examples of mathematical notations do not seem to invoke perceptual elements in the mental representation of an equation, but rather concern certain mathematical conventions. However, this impression is deceptive.

An experiment was conducted on material of spatial proximity, in which the participants were required to evaluate the correctness of the equations presented to them. It turned out that they coped with the task worse if the parameter of spatial proximity between variables was not associated with the order of arithmetic operations [11; 12]. For example, if there is less distance between the numbers to be multiplied than between the numbers to be added, then this makes it easier to assess the correctness of the equation and if the distances are arranged vice versa, it is more difficult. In addition, it was found that if adult participants who have a school-level grasp of algebra were asked to write an equation by hand, they would write variables closer to each other if they were considered a higher operation in terms of the hierarchy or order of operations (for example, multiplication) than variables associated with the operation of a lower hierarchy level (for example, addition) [13]. The researchers assumed that symbols and mathematical operators would automatically activate spatial relationships. As it turned out, the distance to the first character left or right of the equal sign was the maximum [13].

Judging by the available data, the influence of irrelevant visuospatial information only increases with the growth of expertise [14]. In this study, the authors used an online platform to collect data from about 50,000 Dutch schoolchildren who had to evaluate the correctness of the equations. It was found that high school students have a more pronounced relationship between spatial proximity and the order of arithmetic operations: closely spaced variables were interpreted as having priority in terms of the order of operations. This effect is paradoxical, since many researchers of cognitive development have for decades assumed that development proceeds from concrete forms of thinking to more abstract forms. However, the results cited indicate that with increasing expertise, people become more sensitive to the spatial organization of algebraic expressions.

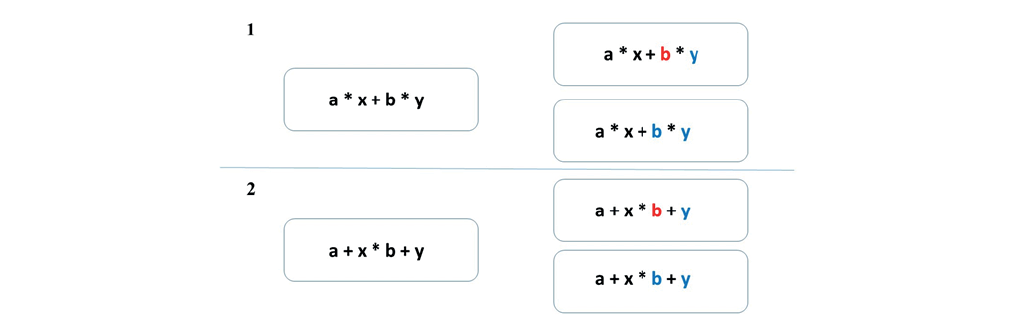
One possible explanation is the mechanism of perceptual learning: the perceptual system can be trained so that the distribution of attention represents a mathematical problem in accordance with the decision-making rules. As an example of one of the studies on the role of attention in solving mathematical equations, one can cite a work where the feature verification paradigm was modified on the basis of algebra [15]. Previously, it was found that checking visual features (for example, color) is easier within one visual grouping than when comparing several features [16]. In a study by Margetis et al., equations like “a * x + b * y” were presented but the color of two neighboring elements changed from black to blue or red (see Fig. 1)

Fig. 1.  The example of stimuli for the study of color verification based on the understanding of symbolic expressions (adapted from [17]). (1) Color verification in the condition of the high-level multiplication operator. (2) Color verification in the condition of the low-level addition operator.

The participants had to state whether the color of these neighboring variables is the same or different. The elements could refer to one arithmetic operation (it might be worth noting that, according to the rules of arithmetic, multiplication is performed before addition), or the elements could belong to different arithmetic operations. It was assumed that the hierarchical organization of the order of operations in the equation will affect the response time about what color the variables are. In particular, if the variables were connected by a multiplication sign, the reaction time for correct answers should have been faster than for variables connected by addition. And so it happened, but only for the participants with a high level of knowledge in the field of algebra. The results led the authors to the conclusion that the perceptual system plays a functional role in determining the correctness of actions for solving equations, and is not just a channel for obtaining information. In another study, using the method of eye movement registration, it was found that when determining the correctness of an equation, eye movement patterns correspond to the syntactic structure of the equation [17].

Based on the results, the authors proposed a hypothesis of reassembly of perceptual-motor systems known as Rigged Up Perception-Action Systems (RUPAS), designed to explain how people manage to successfully operate complex sign systems without the evolutionarily developed cognitive structures and mechanisms for this [18]. The general idea here is that initially, operating with sign systems requires a full set of resource-intensive arbitrarily controlled processes, but as learning progresses, they are automated and replaced by more concise perceptual-motor routines.

Based on this hypothesis and the experimental results obtained, the scientific group of Robert Goldstone developed an interactive system, “Graspable Math”, designed for teaching algebra, in which students can actively manipulate mathematical operators in real time [19]. Such an approach fundamentally avoids linking abstract equations with concrete elements like coins, matches, apples, pies, etc. It is assumed that such a system allows us to understand an important thesis: the variables and operators themselves are, in a sense, concrete objects that can be manipulated. Various types of equation transformations are performed by physical actions to change the spatial arrangement of mathematical objects. At the moment, evidence has already been obtained of the effectiveness of teaching algebra using this system [19; 20]. But it is necessary to evaluate the effectiveness of the proposed approach in comparison with the traditional one.

Understanding Graphs and Charts

Another area of application of the ideas of grounded cognition is data visualization. In the natural sciences, quite often, one has to deal with a visual representation of non-obvious abstract patterns. Therefore, in order to be able to optimize graphs and diagrams, to make them as understandable as possible, it is necessary to study which cognitive processes are involved in this task.

One of the research directions in this area is the study of visual routines [21; 22] that are used in the process of reading graphs and which may affect the final interpretation of a particular image. The very fact that these routines influence the interpretation of a graph already suggests that such representations should be grounded in the perceptual system. In one of the works the authors used the eye-tracking method to determine what exactly happens in the process of understanding histograms [23]. The subjects had to compare the bars of histograms by color or by size. As It was found that when reading this type of graph, people first choose a kind of reference point (in the case of histograms, a specific column in it), with which they compare the rest. It turned out that for histograms of the same color, but different height, such a reference point is most often the highest bar. And if the columns differ in color, but are the same in size, then it is the darkest. However, if the columns differ both in color and size, then the subjects are guided by the attribute that is relevant to the task (that is, how exactly it is worth comparing the columns – by color or by size). Thus, perceptual templates turn out to be task-specific, and if the presented histograms present several options upon which to establish understanding, then the templates contribute to the interpretation by determining the initial reference point. This result is consistent with others obtained in the course of estimating the number of objects on histograms, where the final interpretation of the graph also depended on the selected reference point [24].

A whole series of studies has been devoted to how, when reading color graphs, people match different colors and concepts that define the semantics of the graph [25]. Evidence has been obtained in favor of the fact that histograms reflecting a different number of objects (fruits) are better understood if the color of the bars matches their color [26]. That is, the perceptual characteristics of the graph affect the accuracy of its interpretation. However, as the authors of this study point out, such an effect occurs only if there is a strong association between the color and the semantics of the category displayed on the graph.

Thus, we can conclude that data visualization is more effective the more it follows the principle of isomorphism: the perceptual characteristics of graphs should somehow correspond to the semantics of the displayed categories.

Another direction of research into the groundedness of mental representations in a perceptual system in the field of visualization regards how students generate schemas that visualize the operation of complex systems. In general, it has already been established that if students independently generate some explanations, examples or analogies for the material being studied, then this increases the effectiveness of learning [27; 28]. But how important is the visual format of these explanations and analogies?

There is already evidence that the explanation of educational material accompanied by relevant schemes and diagrams, is more effective than without [29]. In particular, it has been found that, when reading a text about tectonic plates and asking students to draw a diagram to accompany the text, they perform better on a follow-up test of similar content than students who were asked to write a short summary of the text they have read [30]. Similar results were obtained for a text on the law of conservation of energy, the understanding of which was better when students were asked to draw a diagram rather than write their own text [31].

One possible explanation for the advantage of visualizations over verbal descriptions is the need to translate from one representational format to another. Such a translation can help to find gaps and contradictions in the original ideas, and aid in their subsequent development and refinement [32]. In general, this kind of translation might be helpful due to a deeper processing of information. However, another explanation is also possible, that perceptual and verbal representations correspond with each other and, due to such integration, provide an advantage in learning [33].

However, there is also evidence against the use of visualizations in teaching. In particular, it was found that the very drawing of diagrams to understand a text in physics can lead to specific comprehension errors, when an incorrect spatial arrangement of the components on a diagram leads to additional difficulties in understanding the material being mastered [34]. Yet, the author points out that such errors occur only among beginners who have no experience in using diagrams. Thus, the benefits of visualization in learning are mediated by the amount of experience with using diagrams.

At the same time, a number of studies suggest that spatial abilities can play a role as well. In particular, it was found that people with low levels of such abilities spend more resources on building a visual representation, and people with high levels of spatial abilities willingly spend these resources on matching visual and verbal representations [35]. In addition, people with low spatial abilities demonstrate difficulties in the animation of mechanical systems (they can neither imagine exactly how a particular device works nor answer the corresponding questions) [36]. Besides, it has been found that people with low levels of spatial ability tend to perceive visualizations as static pictures [37], while people with higher levels of spatial ability embed visualizations into more complex mental representations and manipulate them effectively.

Finally, one of the best-known studies has shown that if subjects are asked to explain or draw how a device (a bicycle pump) works, information about the structural components of the pump is more accurately learned and presented in the visualization than in the verbal explanation. No differences were found in responses on the function and mechanics of this pump [38]. Furthermore, the authors indicated that, according to the results of their study, visualization still helps people with low spatial abilities in learning, which is generally consistent with the empirical evidence already accumulated in this area. Thus, we can conclude that it is worth suggesting a student draw a diagram in the process of mastering abstract material if he or she has sufficiently low spatial abilities, and also if we are talking about the structure, and not about the functions of the phenomenon being studied.

Summing up, we can point to the potential application of using hybrid representations, combining both perceptual components and abstract amodal ones, in an educational context. The very concept of hybrid representations can be a clue to researchers seeking to uncover the mechanisms that underlie the mediation of conceptual thinking, as well as a point of convergence between modern cognitive research and the cultural-historical approach. In particular, the studies described above can be interpreted as illustrations of how various cultural tools in the form of visualizations (graphs or diagrams), and in the form of a system of mathematical symbols, affect learning processes.

Regarding practical application, the results testify to the perceptual groundedness of abstract representations and can be used in a wide range of educational contexts, ranging from the creation of special software that can suggest to our perceptual system the best ways to assimilate educational material, to local recommendations for working with visualizations and verbal descriptions of complex systems in order to make them more understandable to students. 

1. Loginov N.I., Spiridonov V.F. Voploshchennoe poznanie (embodied cognition): osnovnye napravleniya issledovanii [Key areas of research in the embodied cognition approach]. Vestnik Sankt-Peterburgskogo universiteta. Psikhologiya i pedagogika = Vestnik SPbSU. Psychology and Education, 2017. Vol. 7, no. 4, pp. 343—364. DOI:10.21638/11701/spbu16.2017.404 (In Russ.).
2. Loginov N.I., Spiridonov V.F. Voploshchennoe poznanie kak sovremennyi trend razvitiya kognitivnoi psikhologii [Embodied Cognition as a Current Trend in Cognitive Psychology]. Vestnik Sankt-Peterburgskogo universiteta. Psikhologiya i pedagogika = Vestnik SPbSU. Psychology and Education, 2017. Vol. 7, no. 1, pp. 25—42. DOI:10.21638/11701/spbu16.2017.102 (In Russ.).
3. Madni A.O., Spiridonov V.F. Radikal’nyi podkhod k voploshchennomu poznaniyu: teoriya dinamicheskikh system [Radical approach to embodied cognition: dynamic system theory]. Rossiiskii zhurnal kognitivnoi nauki = The Russian Journal of Cognitive Science, 2018. Vol. 5, no. 3, pp. 37—55. (In Russ..
4. Barsalou L. W. Perceptions of perceptual symbols. Behavioral and brain sciences, 1999. Vol. 22, no. 4, pp. 637—660. DOI: 10.1017/S0140525X99532147
5. Mahon B.Z., Caramazza A. Why does lexical selection have to be so hard? Comment on Abdel Rahman and Melinger’s swinging lexical network proposal. Language and Cognitive Processes, 2009. Vol. 24, no. 5, pp. 735—748. DOI:10.1080/01690960802597276
6. Machery E. Doing without concepts. Oxford University Press, 2009. 283 p
7. Connell L., Lynott D. Principles of representation: Why you can’t represent the same concept twice. Topics in Cognitive Science, 2014. Vol. 6, no. 3, pp. 390—406. DOI:10.1111/tops.12097
8. Yee E., Thompson-Schill S. L. Putting concepts into context. Psychonomic bulletin & review, 2016. Vol. 23, no. 4, pp. 1015—1027. DOI:10.3758/s13423-015-0948-7
9. Dehaene S., Cohen L. Cultural recycling of cortical maps. Neuron, 2007. Vol. 56, no. 2, pp. 384—398. DOI:10.1016/j.neuron.2007.10.004
10. Vygotskii L.S. Istoriya razvitiya vysshih psihicheskih funkcij [The History of the Development of Higher Mental Functions]. Sobranie sochinenij = Collected works. Moscow, 1983. Vol. 3, pp. 5—329 (In Russ.).
11. Landy D., Goldstone R. L. Formal notations are diagrams: Evidence from a production task. Memory & cognition, 2007. Vol. 35, no. 8, pp. 2033—2040. DOI:10.3758/BF03192935
12. Rivera J., Garrigan P. Persistent perceptual grouping effects in the evaluation of simple arithmetic expressions. Memory & cognition, 2016. Vol. 44, no. 5, pp. 750—761. DOI:10.3758/s13421-016-0593-z
13. Landy D., Goldstone R. L. How abstract is symbolic thought? Journal of Experimental Psychology: Learning, Memory, and Cognition, 2007. Vol. 33, no. 4, pp. 720. DOI:10.1037/0278-7393.33.4.720
14. Braithwaite D. W. et al. Non-formal mechanisms in mathematical cognitive development: The case of arithmetic. Cognition, 2016. Vol. 149, pp. 40—55. DOI:10.1016/j.cognition.2016.01.004
15. Marghetis T., Landy D., Goldstone R. L. Mastering algebra retrains the visual system to perceive hierarchical structure in equations. Cognitive research: principles and implications, 2016. Vol. 1, no. 1, pp. 25. DOI:10.1186/s41235-016-0020-9
16. Duncan J. Selective attention and the organization of visual information. Journal of experimental psychology: General, 1984. Vol. 113, no. 4, pp. 501. DOI:10.1037/0096-3445.113.4.501
17. Schneider E. et al. Eye gaze reveals a fast, parallel extraction of the syntax of arithmetic formulas. Cognition, 2012. Vol. 125, no. 3, pp. 475—490. DOI:10.1016/j.cognition.2012.06.015
18. Goldstone R. L. et al. Adapting perception, action, and technology for mathematical reasoning. Current Directions in Psychological Science, 2017. Vol. 26, no. 5, pp. 434—441. DOI:10.1177/0963721417704888
19. Ottmar E. et al. Graspable mathematics: Using perceptual learning technology to discover algebraic notation. Integrating touch-enabled and mobile devices into contemporary mathematics education. IGI Global, 2015, pp. 24—48.
20. Ottmar E., Landy D. Concreteness fading of algebraic instruction: Effects on learning. Journal of the Learning Sciences, 2017. Vol. 26, no. 1, pp. 51—78. DOI:10.1080/10508406.2016.1250212
21. Cavanagh P. Attention routines and the architecture of selection. Cognitive Neuroscience of Attention. New York: Guilford Press, 2004, pp. 13—28.
22. Ullman, S. Visual routines. Cognition, 1984. Vol. 18, pp. 97—159. DOI:10.1016/B978-0-08-051581-6.50035-0
23. Michal A.L., Franconeri S. L. Visual routines are associated with specific graph interpretations. Cognitive research: principles and implications, 2017. Vol. 2, no. 1, pp. 1—10. DOI:10.1186/s41235-017-0059-2
24. Michal A.L. et al. Visual routines for extracting magnitude relations. Psychonomic bulletin & review, 2016. Vol. 23, no. 6, pp. 1802—1809. DOI:10.3758/s13423-016-1047-0
25. Schloss K.B. et al. Color inference in visual communication: the meaning of colors in recycling. Cognitive research: principles and implications, 2018. Vol. 3, no. 1, pp. 1—17. DOI:10.1186/s41235-018-0090-y
26. Lin S. et al. Selecting semantically resonant colors for data visualization. Computer Graphics Forum. Oxford, UK: Blackwell Publishing Ltd, 2013. Vol. 32, no. ¾, pp 401—410. DOI:10.1111/cgf.12127
27. Chi M.T.H. Active-constructive-interactive: A conceptual framework for differentiating learning activities. Topics in cognitive science, 2009. Vol. 1, no. 1, pp. 73—105. DOI:10.1111/j.1756-8765.2008.01005.x
28. Hall V. C., Bailey J., Tillman C. Can student-generated illustrations be worth ten thousand words? Journal of Educational Psychology, 1997. Vol. 89, no. 4, pp. 677. DOI:10.1037/0022-0663.89.4.677
29. Ainsworth S., Loizou Th. A. The effects of self-explaining when learning with text or diagrams. Cognitive science, 2003. Vol. 27, no. 4, pp. 669—681. DOI:10.1207/s15516709cog2704_5
30. Gobert J. D., Clement J. J. Effects of student-generated diagrams versus student-generated summaries on conceptual understanding of causal and dynamic knowledge in plate tectonics. Journal of Research in Science Teaching: The Official Journal of the National Association for Research in Science Teaching, 1999. Vol. 36, no. 1, pp. 39—53. DOI:10.1002/(SICI)1098-2736(199901)36:1<39::AID-TEA4>3.0.CO;2-I
31. Edens K. M., Potter E. Using descriptive drawings as a conceptual change strategy in elementary science. School science and mathematics, 2003. Vol. 103, no. 3, pp. 135—144. DOI:10.1111/j.1949-8594.2003.tb18230.x
32. Ainsworth S., Bibby P., Wood D. Examining the effects of different multiple representational systems in learning primary mathematics. The Journal of the Learning Sciences, 2002. Vol. 11, no. 1, pp. 25—61. DOI:10.1207/S15327809JLS1101_2
33. Aleven V. A., Koedinger K. R. An effective metacognitive strategy: Learning by doing and explaining with a computer-based cognitive tutor. Cognitive science, 2002. Vol. 26, no. 2, pp. 147—179. DOI:10.1207/s15516709cog2602_1
34. Wilkin B. Learning from explanations: Diagrams can “inhibit” the self-explanation effect. Reasoning with diagrammatic representations II: Papers from AAAI Fall Symposium, 1997, pp. 136—143.
35. Mayer R. E., Sims V. K. For whom is a picture worth a thousand words? Extensions of a dual-coding theory of multimedia learning. Journal of educational psychology, 1994. Vol. 86, no. 3, pp. 389. DOI:10.1037/0022-0663.86.3.389
36. Hegarty M., Just M. A. Constructing mental models of machines from text and diagrams. Journal of memory and language, 1993. Vol. 32, no. 6, pp. 717—742. DOI:10.1006/jmla.1993.1036
37. Kozhevnikov M., Hegarty M., Mayer R. E. Revising the visualizer-verbalizer dimension: Evidence for two types of visualizers. Cognition and instruction, 2002. Vol. 20, no. 1, pp. 47—77. DOI:10.1207/S1532690XCI2001_3
38. Bobek E., Tversky B. Creating visual explanations improves learning. Cognitive Research: Principles and Implications, 2016. Vol. 1, no. 1, pp. 27. DOI:10.1186/s41235-016-0031-6