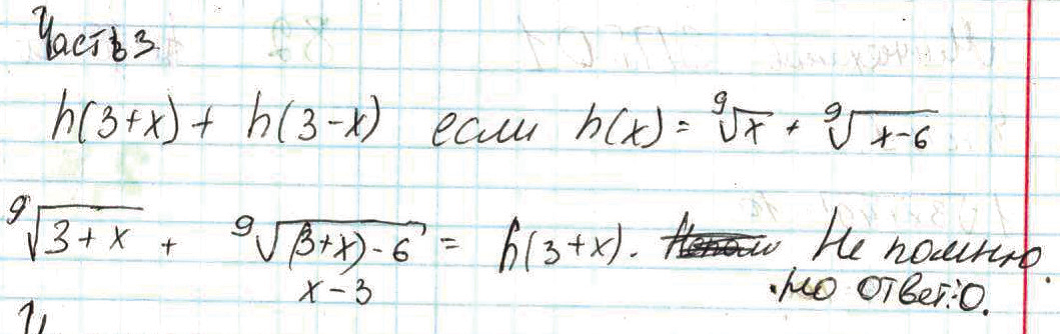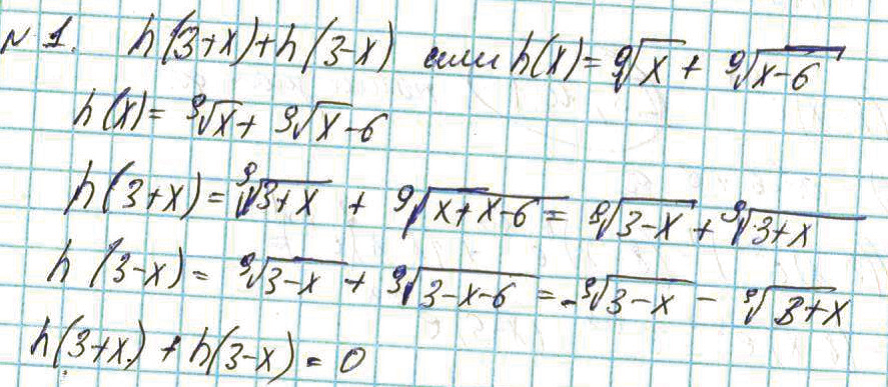Introduction
In the modern world, mathematics education plays a key role in developing critical thinking and analytical skills needed for successful adaptation to rapidly changing technological and social conditions.
Social, cultural, geographical, and economic factors influence the development of students' thinking [Chesters, 2022; Mali, 2022]. According to Rosstat data, 75% of university students come from urban areas, while 21% come from villages and rural settlements. This highlights the importance of research aimed at studying the peculiarities of teaching urban and rural students. Studies [Chesters, 2022] indicate that rural youth generally have lower educational aspirations than their urban peers. In this regard, we should note the results of a team of authors who proposed a model considering regional risks to improve the quality of education in rural schools in Bashkortostan [Gumerova, 2023]. R. Parsons [Parsons, 2022] was among the first to identify the mismatch of social and cultural contexts as a barrier to education for rural and non-rural youth. On one hand, this difference lies in the socioeconomic status between rural and urban families [Koricich, 2018], and on the other, in the professional aspirations of rural and non-rural youth [Francis, 2022].
In exploring the development of students’ mathematical skills and identifying influencing factors, researchers examined thought structures, math anxiety [Asherft, 2019], and emotional experience [Mali, 2022]. The significance of these factors for the development of mathematical skills is confirmed by numerous studies (see, for example, [Vygotsky, 1999; Piaget, 1983; Asherft, 2019]), including [Shvarts, 2011; Mali, 2022] which discuss their influence on the understanding of mathematics. Although there are differing opinions on the phenomenon of mathematical understanding (see, for example, [Kuzniak, 2022; Tuktamyshov, 2022a]), the number of studies in this area has recently been increasing, particularly among foreign researchers (see the review [Şefik, 2021]; among domestic studies, see [Gromova, 2014]).
This study applies the APOS theory, which emphasizes sequential development of mathematical concepts through internal construction and reflection. This theory was specifically designed to study mental structures in the process of learning mathematics. Based on the principles of constructivism and drawing on the works of J. Piaget [Piaget, 1983], APOS theory was developed by E. Dubinsky [Dubinsky, 2002] to analyze the structuring of mathematical concepts in students' minds. According to APOS theory, mental constructions rooted in reflective abstraction [Dubinsky, 2002] are defined as Action, Process, Object, and Schema. Arnon and other researchers [Arnon, 2014] describe APOS as “a theory of how mathematical concepts may be learned.” Detailed descriptions of APOS applications in mathematics education are provided in the review article [Şefik, 2021].
The choice of this research topic stems from the limited study of how regional educational conditions influence the understanding of mathematical concepts. While the external factors mentioned earlier implicitly affect the stages of APOS, this study focuses on determining the degree of mathematical concept formation among students through the lens of APOS theory in a regional context.
Problem Statement: How do regional differences in secondary education (urban versus rural) impact the formation of mathematical concepts in students?
Objective: The purpose of this study was to determine the extent of mathematical concept formation among students in the context of social and geographical diversity using APOS theory. It was hypothesized that students’ social and geographical backgrounds and their level of basic mathematical training influence their degree of concept formation. This is reflected in the quantity and nature of conceptual and procedural errors at each stage of APOS theory. Consequently, the study focuses on analyzing students’ errors at various stages of understanding mathematical concepts.
To achieve this objective, the following tasks were identified:
– Determine how students from different geographical (urban, rural) and social contexts understand and apply basic mathematical concepts at each stage of APOS theory;
– Conduct a comparative analysis of the frequency and types of errors at APOS stages across different groups of students.
Methods
As mentioned above, this study used APOS theory, developed by E. Dubinsky and colleagues [Arnon, 2014], as its theoretical foundation. APOS theory (Action-Process-Object-Schema) is a modification of Piaget’s ideas on reflective abstraction [Piaget, 1983], applied to the analysis of mental structures necessary for learning mathematics (see [Arnon, 2014] for details). Reflective abstraction focuses on universal characteristics of actions unrelated to the specific mathematical objects being manipulated [Shvarts, 2011].
Within APOS, an Action is defined as manipulation of an already existing mathematical object that the student perceives as external. Actions are based on rules and algorithms that students repeatedly practice under the teacher’s guidance and are tied to specific objects. When an Action is repeated and the student responds to it, it can transform into a Process, shifting from the external to the internal realm. This stage involves internalizing actions into procedures, enabling students to independently perform actions or generalize them into processes valid for the same type of mathematical object.
When the context in which the student constructs the Process changes, the student may need to act on the Process itself to understand new problem situations. In this case, the student must perceive the Process as a unified entity, as an independent object. If the student is able to perform or imagine actions on the Process, it is said to be encapsulated into an Object. In the context of functions, this means that the student can, for example, determine intervals of increase and decrease of functions. Actions, Processes, Objects, and other previously created mental structures associated with a given mathematical concept can be combined into a single structure known as a Schema. The Schema is activated in response to a problem situation that the student perceives as an instance of a specific mathematical concept.
The main methods used in this study were:
– A systematic approach to analyze scholarly and pedagogical publications on the research topic, to identify and synthesize the theoretical foundations of the problem;
– Content analysis of survey results, to evaluate the understanding of mathematical concepts according to APOS theory;
– Statistical analysis methods: Mann–Whitney U test, Shapiro–Wilk test, and Kruskal–Wallis test.
This study analyzes students’ errors at various stages, offering ways to address them.
The empirical stage of the research was conducted at Kazan State University of Architecture and Engineering. The study proceeded in stages:
-
Theoretical stage: Establishing the premises of the research and creating a survey to assess students’ readiness to understand and determine their stages of mathematical concept understanding according to APOS theory.
-
Experimental stage: Conducting the survey to identify errors and assess students’ understanding of mathematical concepts, followed by analysis of the results.
The survey included 96 first-year students, 57 of whom were female and 39 male, enrolled in the “Construction” program at Kazan State University of Architecture and Engineering (KSUAE). The students were aged 17–18 years.
A questionnaire developed by the authors was used, consisting of typical Unified State Exam (USE) tasks sourced from an educational portal for exam preparation “Reshu EGE” (https://ege.sdamgia.ru/) and adapted to APOS theory. The survey assessed the formation of mathematical concepts (algebraic expressions, functions, derivatives, solving equations and inequalities, function graphs) among students. The USE tasks were used for the Action and Process stages. Examples of tasks included:
Part 2 (Process):
1.Find the minimum value of a function on a segment .
on a segment .
2.Find the point of minimum of a function 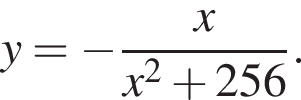 .
.
This example illustrates tasks aimed at evaluating students’ ability to understand and perform sequential actions or algorithms—key characteristics of the Process stage in APOS theory.
Results
Based on the data analysis, the information was categorized by social component, dividing settlements into three groups: Kazan, other cities, and villages/rural areas. Another important factor was the USE score, divided into two categories: 40–64 points and 65–100 points, reflecting the baseline level of mathematical knowledge. The threshold of 65 points was chosen as the average USE math score for students admitted to technical universities in Kazan (KSUAE, Kazan State Power Engineering University, Kazan National Research Technological University) in 2023 was 65 points.
The following data were obtained from the survey participants:
Table. Quantitative and qualitative composition of survey participants
|
USE Score\Location |
Kazan |
Other cities |
Villages (rural areas) |
Total |
|
40-64 |
15 |
13 |
4 |
32 |
|
65-100 |
19 |
28 |
17 |
64 |
|
Total |
34 |
41 |
21 |
96 |
Analyzing the data, it can be noted that two-thirds of the first-year cohort scored above 65 on the USE. Additionally, 35.4% of all first-year students were from Kazan, 42.7% came from other cities (small towns) in Tatarstan and Russia, and 21.9% were from rural areas. Among first-year students scoring above 65, only 29.7% were from Kazan, while 43.8% came from other cities, and 26.5% were from rural areas. The majority of high-scoring students, therefore, came from other cities.
Further analysis of the proportions of first-year students from each group (Kazan, other cities, rural areas) with scores above or below 65 reveals that among those from Kazan, 55.8% scored above 65, while 44.2% scored below. For other cities, the distribution was 69.2% scoring above 65 and 30.8% scoring below. For rural areas, 80.9% scored above 65 and 19.1% below.
Following [Şefik, 2021], errors were classified as conceptual and procedural, although other classification methods exist [Dalinger, 2014]. Conceptual errors indicate a lack of understanding of the problem’s essence, failure to grasp relationships within the problem and between concepts. Procedural errors occur due to incorrect execution of operations or algorithms, revealing difficulties with technical, formal transformations even when basic concepts are understood. This approach to error analysis through APOS theory has proven highly productive, particularly in the topic of “Differentiation” [Siyepu, 2015]. Conceptual and procedural errors were diagnosed using a questionnaire designed around APOS stages, analyzing responses to identify errors, and manually reviewing and scoring answers. Results of the Shapiro–Wilk test for data from Kazan, rural areas, and other cities showed that the data were not normally distributed. The Kruskal–Wallis test for each stage (Action, Process, Object, Schema) revealed no statistically significant differences in procedural errors across the three groups. However, for conceptual errors at the Schema stage, statistically significant differences were found (p = 0.001, which is well below the significance level of 0.05). Pairwise comparisons using the Mann–Whitney test followed.
Let us present the results of the analysis of procedural errors made by students (see Fig. 1).
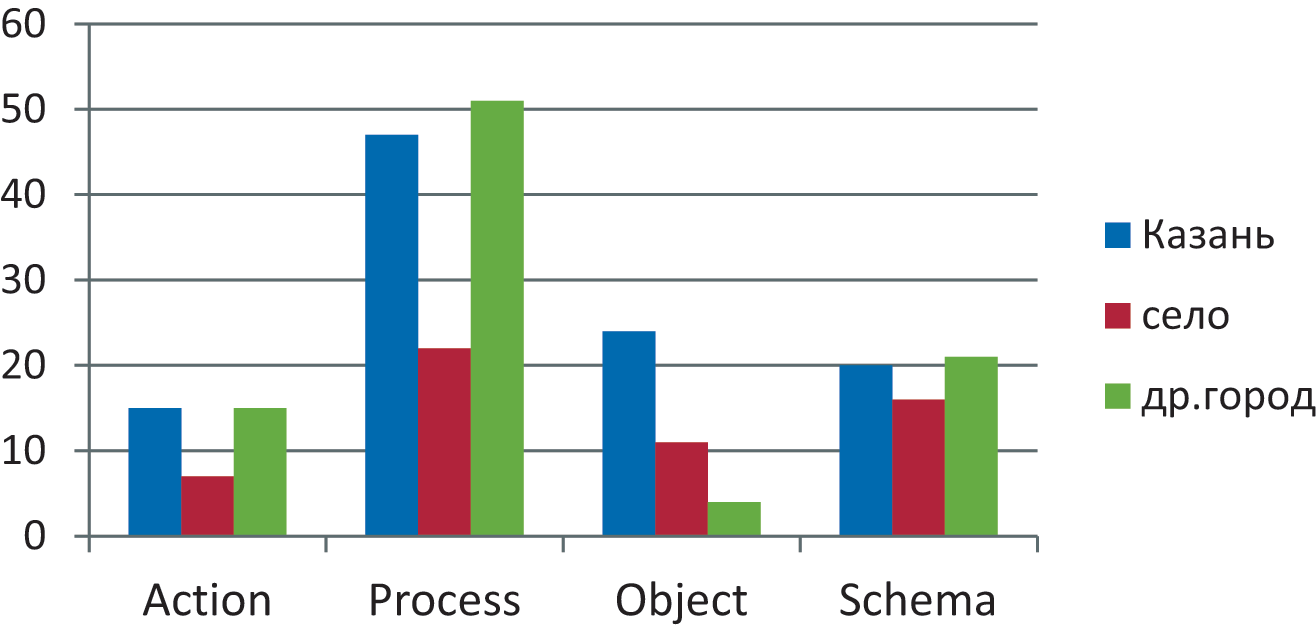
Fig. 1. Diagram of the distribution of procedural errors by APOS stages for students from Kazan, rural areas and other cities: on the vertical axis, divisions are marked (from 0 to 60), corresponding to the number of procedural errors
Procedural errors were most common during the Process stage across all groups. Common procedural errors included incorrect use of parentheses and substitutions, arithmetic mistakes, and failure to eliminate extraneous roots. Rural school graduates made fewer errors overall compared to others. The Mann–Whitney test showed no statistically significant differences in the number of procedural errors between different locations at a significance level of 0.05.
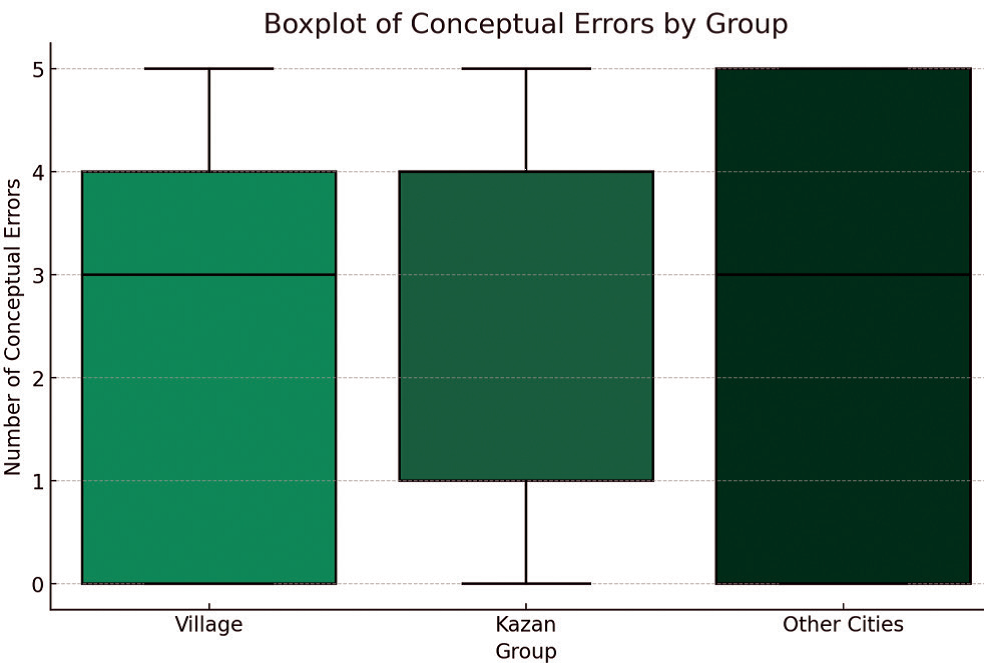
Conceptual errors were compared at the Object and Schema stages since these stages are more indicative of students’ understanding of mathematical concepts. Let us present a graphical representation (Fig. 2) for the analysis of conceptual errors at the Object stage using Boxplot [Benjamini, 1988].
Fig. 2. Graphical representation of conceptual errors at the Object stage
Boxplot visually displays five numerical characteristics of data: minimum, first quartile (Q1), median, third quartile (Q3), and maximum, as well as outliers.
A statistical analysis conducted at the Object stage showed that the p-value for rural areas and Kazan was p=0.6496; for rural areas and other cities, p=0.5804; and for Kazan and other cities, p=0.35133. In all comparisons, the p-values were above 0.05, indicating no statistically significant differences in the number of conceptual errors among students from rural areas, Kazan, and other cities at the Object stage. Median values were 3.0 for rural areas and other cities, and 4.0 for Kazan.
An analysis of conceptual errors at the Schema stage revealed statistically significant differences between Kazan and rural areas (p=0.0035), as well as between Kazan and other cities (p=0.0007). No significant differences were found between rural areas and other cities (p=0.7254).
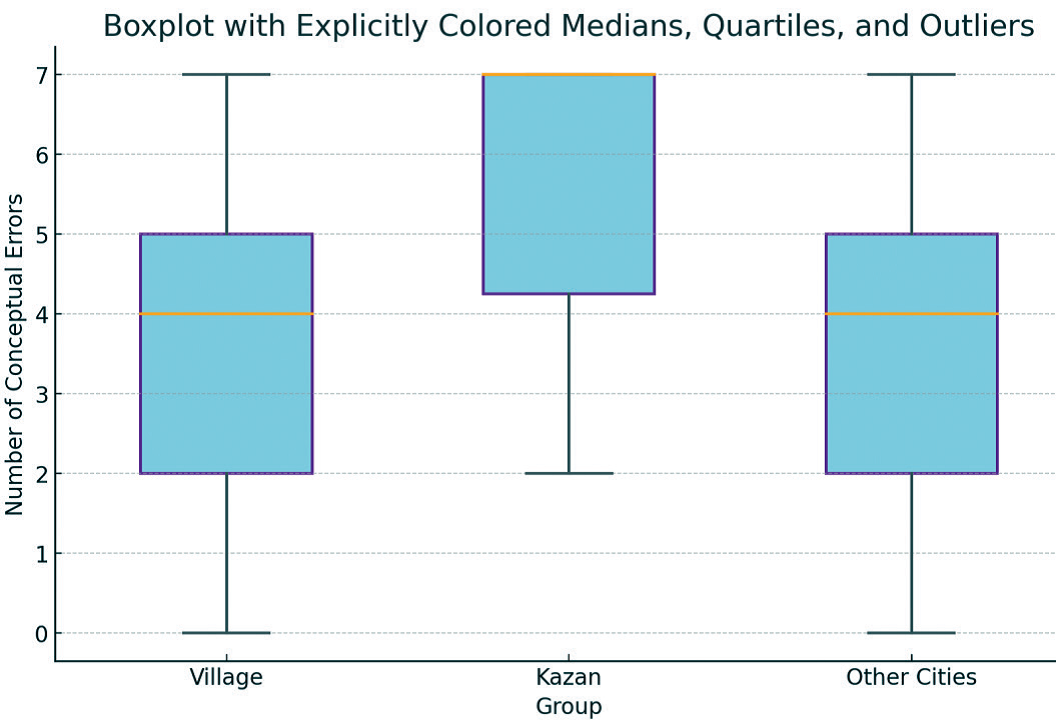
To visually present the differences between the groups (rural areas, Kazan, and other cities), we include a Boxplot (Figure 3) showing the distribution of the number of conceptual errors for each group at the Schema stage, with median values highlighted in yellow.
Fig. 3. Graphical representation of conceptual errors at the Schema stage
The presented Boxplot shows that the median number of conceptual errors in Kazan (7.0) is higher than in rural areas and other cities (both 4.0), with a larger spread of errors. The distributions in rural areas and other cities are similar, with less variability. The median is 7 because the value at the midpoint of the data is 7. Q3 is also 7, as 75% of the data falls at or below this value, and all surrounding data points are also 7. This means that, while not all 34 students make exactly 7 errors, a significant number of them (22 out of 34) do.
The results of the Mann-Whitney test confirm statistically significant differences between Kazan and the other groups, while there are no differences between rural areas and other cities.
For illustration, we provide examples of typical procedural and conceptual errors.
Fig. 4. An example of a conceptual error in a student’s work
In Figure 4, it is clear that no solution is provided. The task required substituting (3+x) and (3-x) as arguments into the given function h(x), then simplifying the resulting expression. It is evident that this is a conceptual error, as the student did not understand the task’s instructions.
The next example (Figure 5) relates to the same task, but here it involves a procedural error in the form of a typo.
Fig. 5. An example of a procedural error in a student’s work
A typo occurred during the substitution: in the third line, the second term under the square root incorrectly has "x" instead of the number 3. That is, under the square root it says "x+x-6" when it should have been "x+3-6."
Additionally, we note that the data on which these studies are based is presented in article [Tuktamyshov, 2024].
Discussion
Following [Kuzniak, 2022], step-by-step analysis of the cognitive process helps reveal the relationship between mathematical activity and mathematical thinking. The novelty of our study lies in identifying the impact of social factors on students’ mathematical concept formation. APOS stages, as a framework, help uncover gaps in education and student potential. However, the study did not explicitly consider teaching quality, socioeconomic status, psychological characteristics, or students’ prior educational experiences.
Data analysis shows that most students are at the Action stage of learning differential calculus, highlighting weaknesses in critical thinking [11. Azizi H, 2020]. Experiments revealed that procedural errors stem from insufficient knowledge of school material on functions, elementary algebraic transformations, and connections between mathematical symbols and their visualization, aligning with findings from [Tuktamyshov, 2022].
Rural and out-of-town students showed better results compared to Kazan graduates, especially at the more advanced APOS stages. The high number of conceptual errors among Kazan students at the Schema stage is associated with difficulties in analyzing function graphs and solving irrational equations.
Students who scored above 65 on the USE performed better at all APOS stages compared to those who scored below 65, confirming the relevance of USE scores as an indicator of mathematical knowledge.
Conclusion
Theoretical and experimental results from this study lead to several conclusions:
- Applying APOS theory to analyze differences between urban and rural students helps identify barriers to learning mathematics and develop teaching strategies tailored to their educational backgrounds. This includes adapting instructional materials and methods and creating supportive programs that foster the critical APOS learning stages.
- Students’ errors are both conceptual and procedural. Differences in procedural errors between student groups at the Action and Process stages are not statistically significant and may be random. Conceptual errors generally occur at the Object and Schema stages, highlighting difficulties in deep understanding of mathematical concepts. At the Schema stage, statistically significant differences exist between Kazan and rural areas, as well as between Kazan and other cities.
- The practical significance of this research lies in the ability to monitor students’ academic performance, assess their understanding of mathematical concepts, and organize group discussions that help transform isolated actions into coherent processes.
Future research prospects include studying the effectiveness of pedagogical interventions and technologies to reduce conceptual and procedural errors at different APOS stages, the impact of modern technologies and innovative teaching methods on students’ mathematical concept formation, and cross-cultural studies.