Введение
Процедуры тестирования все чаще используются во многих современных приложениях, требующих оценки поведения людей или машин. Согласно традиционным моделям, основанным на классической теории тестирования, для измерения уровня определенного умения или способности испытуемого настолько точно, насколько это возможно, эти процедуры должны включать большое количество заданий, затрудняющих использование тестов. Выход из этой ситуации обеспечивает компьютеризированное адаптивное тестирование (CAT), развитию которого в значительной мере способствовали современные технологии и вычислительные возможности, появившиеся наряду с разработкой современной теории тестирования (IRT). Использование IRT или других подходов CAT — это метод администрирования тестов и измерения латентных конструктов с помощью небольшого количества тестовых заданий и как можно более точно (Thompson, Weiss, 2011). Эти конструкты могут включать в себя: способности, отношения, знания, навыки, черты и другие соответствующие категории. Ниже термин «конструкт» будет использоваться в качестве замены любой из этих категорий.
Во время компьютеризированной процедуры адаптивного тестирования используется адаптивный принцип выбора заданий, в соответствии с которым трудность заданий, предлагаемых для выполнения, должна соответствовать оценкам уровней достижений испытуемых. Согласно IRT, этот подход дает лучшую дифференциацию испытуемых по уровню их достижений. Другое преимущество представляет многомерное компьютеризированное адаптивное тестирование (MCAT), также включающее более короткое время тестирования и более точную и эффективную оценку конструкта. MCAT объединяет теоретические и практические достижения, полученные в CAT, позволяет получить доступ к большему количеству интересуемых конструктов, не увеличивая нагрузку на инструмент в виде дополнительных пула заданий, и, в конечном итоге, имеет большую точность (т. е. низкую стандартную ошибку измерения) (Torre de la, Patz, 2005). Несмотря на все эти преимущества, доступные методы CAT и MCAT, основанные на IRT, довольно сложны для реализации и не учитывают ряд специальных параметров таких, как время, историю тестирования и т. д.
Однако основная проблема, связанная с CAT и MCAT на основе IRT (которые обычно сочетаются с оценками максимального правдоподобия), состоит в приблизительном равенстве вероятностей для неправильных и правильных решений, поскольку трудность выбранного задания должна соответствовать оценке уровня достижений испытуемого. Этот факт делает результаты тестирования зависимыми в основном от посторонних случайных факторов, которые не связаны с изучаемыми конструктами, тем самым девальвируя полученные выводы, которые становятся фиктивными. Поэтому разработка новых подходов к CAT и MCAT является актуальной проблемой.
Ниже представлен один из подходов к ее решению. Используемая модель представлена марковскими процессами с дискретными состояниями и дискретным временем (цепями Маркова). Особенностью данного подхода является определение трудностей заданий с использованием предельных распределений вероятностей пребывания в состояниях, полученных с помощью матриц вероятностей перехода. Преимущества представленного подхода по сравнению с адаптивным тестированием на основе теории IRT, использующей модель Г. Раша, заключаются в следующем:
1) оценка не выводится из локальных сопоставлений текущих измерений оценок и трудностей с использованием модели Г. Раша, но учитывает:
— всю наблюдаемую историю выполнения тестовых заданий, которая включает в себя распределение успешных и неуспешных решений заданий и их порядок;
— время, затраченное на выполнение тестовых заданий;
2) оценки основаны на прогнозируемых результатах в будущем, при условии, что время тестирования не ограничено, и они не используют локальные (то есть для определенного задания) сравнения, основанные на модели Г. Раша, которые могут быть неустойчивыми1;
3) количество заданий, которые необходимо выполнить, существенно меньше;
4) выбранные трудности заданий связаны с историей выполнения тестовых заданий и не зависят напрямую от текущих приближенных оценок уровней достижений испытуемых;
5) существует возможность учитывать изменение трудности конструктов для испытуемого во время процедуры тестирования из-за усталости и других причин;
6) имеется возможность самообучения, которая приводит к улучшению характеристик модели адаптивного тестирования во время ее эксплуатации;
7) существует процедура идентификации модели, основанная на простых и доступных результатах наблюдений.
В то же время представленный подход может рассматриваться как расширение 1ИТ, поскольку модель Г. Раша используется в качестве ее компонента.
Преимущества представленного подхода по сравнению с адаптивным тестированием на основе марковских моделей с непрерывным временем состоят в следующем:
1) вместо марковских процессов с непрерывным временем используются марковские процессы с дискретным временем (Куравский и др., 2013; Куравский и др., 2011; Кигаузку е1 а1., 2016; Кигаузку е1 а1., 2015), однако в рассматриваемой адаптивной модели время, затрачиваемое на выполнение заданий, учитывается с помощью ограничений на время пребывания в состояниях и переходов в состояния-«ловушки»;
2) допустимы политомические задания.
Модель адаптивного тестирования
Общее описание модели
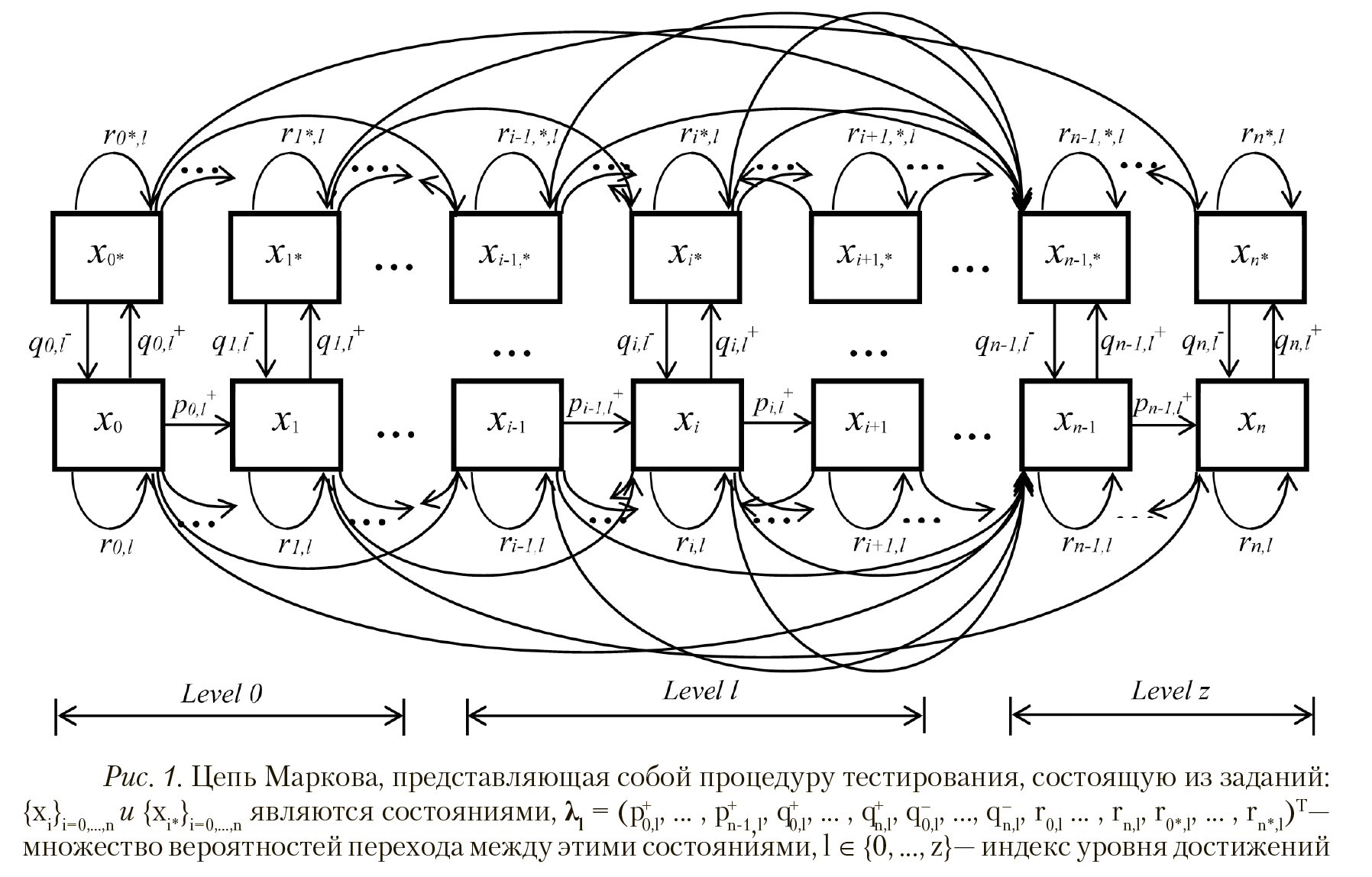
Используются марковские процессы с дискретными состояниями и дискретным временем (цепи Маркова), при этом вероятности перехода между их состояниями являются параметрами модели. Типичная структура, показанная на рисунке 1, представляет собой конечную цепочку из 2п + 2 состояний, в которой переходы из состояния х. (г*0,г^п) возможны только в следующее состояние хг или состояния х * Доступными из состояний хд и хп являются только состояния х1, х и х соответственно. Будучи в состоянии х (г=0,...,п), можно перейти только к состоянию х.
Состояния х. и х* соответствуют г-му уровню трудности заданий. Для каждого г определен конкретный набор заданий соответствующей трудности. Как показано на рисунке 1, состояния с большим номером определяют задания, соответствующие большему уровню трудности, причём задания, соответствующие к самому высокому уровню трудности, соотносятся с состоянием, находящимся в крайнем положении справа.
Предполагается, что каждый испытуемый имеет один из указанных уровней достижений с индексами I е {0, ..., г}, где (г + 1) — число этих уровней, причём каждому из этих уровней соотносится набор заданий определённой трудности и г < п. На каждом уровне достижений задания соответствуют определённому уровню знаний, способностей или навыков.
Каждый уровень достижений соответствует определенному интервалу трудностей заданий, содержащему не менее одного состояния (см. рис. 1). Поэтому количество уровней трудностей равно или больше, чем количество уровней достижений.
Вероятности пребывания в состояниях модели как функции времени определяются следующим матричным уравнением:
p(t + 1) = M(λl )p(t),
где t — дискретное время; 0 ≤ t ≤ T; t, T ∈ N; T — конечный момент времени; N — множество натуральных чисел; p(t) = (p0 (t), ... , pn (t), p0* (t), ... , pn*(t))T — представляет вероятности пребывания в состояниях модели в момент времени t; M(λl ) = ǁmij(λl )ǁ — стохастическая квадратная матрица вероятностей перехода между состояниями цепи Маркова, в которой mij(λl ) — вероятность перехода из состояния j в состояние i; λl = (p+ 0,l , ... , p+ n-1,l , q+ 0,l , ... , q+ n,l , q– 0,l , ... , q– n,l , r0,l ... , rn,l , r0*,l , ... , rn*,l )T — упорядоченное множество рассматриваемых вероятностей перехода для уровня достижений l. Квадратные матрицы M(λl ) имеют порядок 2n + 2.
Классификация испытуемых выполняется так, как представлено в разделе 2.
Если шкала измерения непрерывная, то весь диапазон ее значений следует разделить на несколько интервалов, каждый из которых интерпретируется как некоторый уровень, определяемый состоянием. Это и есть интервал значений шкалы, который должен быть выбран в результате процедуры тестирования. Чем больше число состояний, тем точнее оценка. Чем точнее оценка, тем большее количество эмпирических данных требуется для настройки модели.
Процедура тестирования определяется администрированием заданий, успешное выполнение которых требует наличия необходимого уровня достижений. Трудность задания, направленного испытуемому, соответствует состоянию модели, занятому им в текущее время.
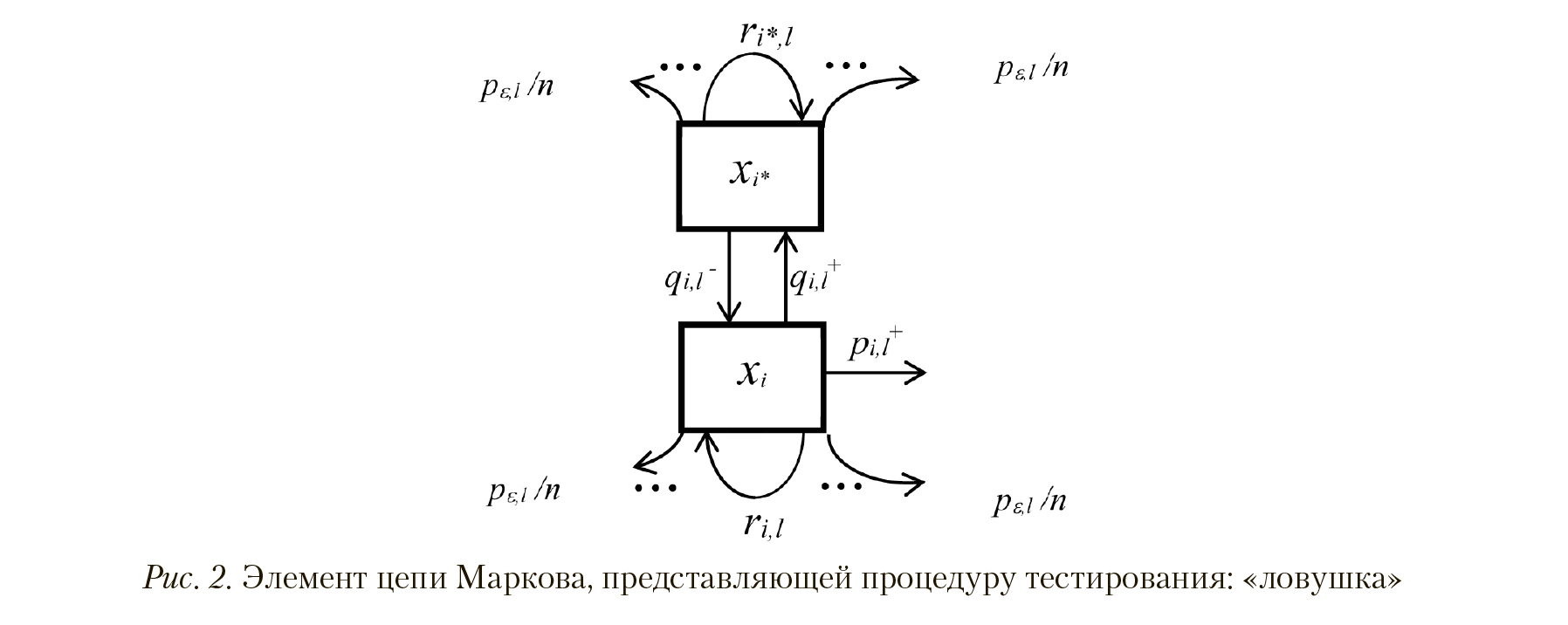
Вероятности перехода вычисляются следующим образом
(i = 0, … , n): q– i,l = p(i, l)k(t * i , i, l)(1 – pε,l), ri,l = (1 – p(i, l)) k(t * i , i, l)(1 – pε,l), ri*,l = ((1 – p(i, l)) k(t * i , i, l) + (1 – k(t * i ,i, l))) (1 – pε,l), q+ i = (1 – k(t * i , i, l)(1 – pε,l), ea(f(l) – i) p(i, l) = 1+ ea(f(l) – i) , с p+ i,l определяемым для i = 0, ... , n – 1: p+ i,l = p(i, l)k(t * i , i, l) (1 – pε,l), где функция p(i, l
где функция р(г, /) выражает зависимость Г. Раша для вероятности успепнного выполнения тестового задания на уровне достижений / и уровне трудности задания I; параметры к(£\ , I, /) представляют вероятности непревышения соответствующих временных ограничений 1\ в случае заданных уровней трудности I и уровней достижений /; ре/ << 1 (/ е {0, ..., г}) — вероятность «ошибки» для каждого состояния, принадлежащего уровню достижений /; функция/(/) и величина а являются параметрами модели Г. Рата. .Малые I;с|)о>ггнос1'11 р соответствующие уровням достижений, необходимы для поддержки адаптивности, поскольку эти значения отвечают за переходы, которые выполняются в случае изменения текущих оценок уровней достижений. Предполагается, что они равномерно распределены по соот1;с'гству|<ищиI переходам из каждого состояния и, следовательно, равны рв1 / п. Включение небольшой вероятности «ошибки» в модель необходимо для формальных переходов, которые маловероятны для определенного уровня достижений, но характерны для какого-либо другого уровня дости/Псы 1111, в противном случае эти переходы были бы невозможны. Этот элемент модели полезен при классификации испытуемых. Малые вероятности перехода усредняются, поскольку их значения имеют порядок ошибки выборки (несмотря на то, что их можно оценить с использованием экспериментальных данных).
Появление в модели «ловушек», показанное на рисунке 2, обусловлено как необходимостью учитывать временную динамику процедуры тестирования (время учитывается в модели неявно), так и возможностью дифференцировать две важные группы испытуемых: тех, кто быстро генерируют ряд неправильных решений, и тех, кто находит правильное решение в течение длительного периода времени. Это важно для психологической диагностики, поскольку данная функция позволяет определять тех, кто не критичен в отношении получаемых ими результатов. Когда t*^ ,, соответствующие «ловушки» трансформируются из структуры с двумя состояниями в структуру с 1-м состоянием.
Правила переходов и классификация
В начальный момент процедуры тестирования предполагается, что испытуемый находится в состоянии модели xg, т.е. получает самое простое задание (отвечающее самому нижнему уровню конструкта).
Когда испытуемый находится в состоянии xk, то предъявляемое задание выбирается случайным образом из набора заданий, соответствующих данному состоянию, с временными ограничениями t* применяемыми для каждой пары состояний цепи Маркова (x., x*).
Переходы испытуемого между состояниями определяются следующими правилами:
— если в состоянии xt испытуемый правильно выполняет назначенное задание, и время выполнения не превышает заданное значение t* (т. е. завершает назначенное задание в течение заданного периода времени), то он переходит в состояние x.+1;
— если в состоянии x. испытуемый неправильно выполняет назначенное задание, а время выполнения не превышает заданное значение t*, то он остается в состоянии x.;
— если испытуемый находится в состоянии x., а время выполнения назначенного задания превышает заданное значение t*i, то испытуемый переходит в состояние x *;
— если испытуемый находится в состоянии x и время выполнения назначенного задания либо превышает заданное значение t*i, либо испытуемый неправильно выполняет назначенное задание, а время тестирования не превышает заданного значения t*i, то испытуемый остается в состоянии x ;
— если, находясь в состоянии x , испытуемый правильно выполняет назначенное задание, а время выполнения не превышает заданное значение t*i, то испытуемый возвращается в состояние x .
После каждого из указанных переходов выполняется коррекция состояний посредством классификации. Классификация осуществляется для определения уровня достижений испытуемого. Применяется подход, основанный на вычислении предельного стационарного распределения p,,z = (p,,z, ... , p,,z, p”,z , ... , P,,z)T рассмотренных вероятностей состояний цепи Маркова, которые удовлетворяют следующему уравнению:
p ', = M(X;)p”,z.
Доказано, что распределение p,,z является собственным вектором выбранной в данный момент стохастической матрицы M(X;), которая всегда существует и соответствует единичному собственному значению. В случае рассматриваемых матриц M(X;) было также обнаружено, что процесс p(t) эргодичен, другие собственные значения данной матрицы находятся строго внутри единичной окружности в комплексной плоскости, p,,z = lim, pz (t). Численные методы вычисления p,,z довольно просты и могут быть найдены в соответствующей литературе (Burden, Faires, 2001; Wilkinson, 1988).
Чтобы учесть траектории движения испытуемого между состояниями рассматриваемых цепей Маркова и сделать классификацию на основе распределения p,,z более надежной и более подходящей реальной ситуации, столбцы матриц M(X;), где Z е {0, ..., z}, корректируются после каждой попытки выполнить задание, а именно: в случае перехода между состояниями модели, соответствующим индексам j и i этих матриц (из состояния j в состояние i) элемент т.. заменяется на 1, а другие элементы столбца j заменяются на 0, причем эти изменения остаются действительными только для процедуры тестирования данного испытуемого. Матрица М(Х;), в которой такие изменения были осуществлены, называется матрицей пройденной траектории. После каждого шага процедуры тестирования матрицы пройденных траекторий вычисляются для каждого исследуемого уровня достижений. Таким образом, они сохраняют информацию о динамике тестирования.
Используя матрицы пройденных траекторий, для прогнозирования уровня достижений I испытуемого, после каждой попытки выполнить задание рассчитывается математическое ожидание индекса конечной пары состояний (х, хе„) цепи Маркова:
е, = 1 (р?1+Р7Л
Для дальнейших оценок перед процедурой тестирования для каждого рассматриваемого уровня достижений I и матрицы М(Х;), используемой в начальный момент времени процедуры тестирования, должен быть определен стационарный индекс уровня трудности е? г Чтобы выбрать уровень достижений, который лучше всего подходит для исследуемого процесса тестирования, следует рассчитать абсолютные разности между полученным индексом ег и стационарными индексами уровня трудности е? г для каждого рассматриваемого уровня достижений I (см. рис. 1) и затем выбрать минимальное значение етл.
emnn = , \в1 - ''-, l\'
l E {0 Z} '
Уровень 1тп, соответствующий этому значению етп, дает наилучшую оценку уровня достижений. Очевидно, что чем больше испытуемый соответствует данному уровню достижений, тем меньше значения етП и наоборот.
Если уровень I отличается от текущего, уточнение состояния реализуется с помощью перехода к состоянию, которое соответствует уровню I и имеет целый индекс, который ближе всего соответствует математическому ожиданию е. Уточнение состояния не производится, если либо оно требует уменьшения номера состояния после правильного решения задания, либо номер состояния увеличивается после неправильного решения задания или превышения установленного для решения лимита времени. Также целесообразно выполнять эти сдвиги номера состояний, только если они не превышают заданного порога сдвига. Если какая-либо матрица пройденной траектории повторяется на предыдущих этапах процедуры тестирования, то должно выполняться уменьшение номера состояния. Используемое значение сдвига может меняться со временем.
Матрица М(Х;) для данного уровня достижений I называется согласованной, если упомянутое выше математическое ожидание попадает в набор состояний модели, соответствующих этому уровню (см. рис. 1).
При выполнении описанной здесь процедуры испытуемый «захватывается» в одном из состояний, которое наилучшим образом соответствует оценке его уровня конструкта.
В качестве альтернативного метода для классификации могут быть использованы байесовские оценки. Зная состояние модели, в котором испытуемый оказывается после решения последнего задания в определенный момент времени, и вероятности нахождения в этом состоянии в указанное время для каждого уровня достижений, которая может быть рассчитана с использованием ранее данного матричного уравнения, можно оценить последующие вероятности уровней достижений с помощью формулы Байеса:
P(Cl )P(S│Cl ) P(Cl │S) = ∑z k=0 P(Ck ) P(S│Ck )
где С1 — событие, указывающее, что испытуемый достиг уровня достижений 1(1 е {0, ..., г}), 5 — событие, указывающее, что испытуемый находится в указанном состоянии модели, соответствующем заданному уровню трудности задания в заданное время, Р(С) — является априорной вероятностью достижения испытуемым уровня достижений I, Р(51 С) — вероятность находиться в указанном состоянии модели в указанное время, при условии, что испытуемый имеет уровень достижений I, а Р(С11 5)— это вероятность попадания в уровень достижений I при условии, что испытуемый находится в заданном состоянии модели в указанное время.
Уровень достижений, при котором достигается максимальная условная вероятность Р(Стах | 5) = тах{Р(С11 5)}1 =0 г, дает требуемую классификацию. В результате выполнения последовательности заданий получается распределение вероятностей {Р(С; | 5)} =0 г, что позволяет оценить надежность производной классификации.
Идентификация модели
Идентификация рассмотренных марковских моделей выполняется, используя результаты тестирования. Каждый уровень достижений I е {0, ..., г} обрабатывается отдельно и имеет свою идентифицированную матрицу М(Х;), с которой связан уникальный набор оценок параметров модели Х;. Это позволяет проводить дальнейшую классификацию, вычисляя уровень достижений, который наилучшим образом подходит для проверяемой процедуры тестирования.
В отличие от подхода, представленного в работах (Куравский и др., 2013; Куравский и др., 2011; Кигаузку е1 а1., 2016; Кигаузку е1 а1., 2015, по. 21), идентификация исследуемой модели не требует решения сложных задач оптимизации. Если имеется соответствующая база данных с результатами наблюдений, настройка модели сводится к довольно простой оценке следующих характеристик: функции /(г), величины а, коэффициента к(7* , г, й) и предельного времени {7* } ,_0 п. База данных должна позволять оценивать частоты правильных и неправильных решений для каждой комбинации уровней достижений испытуемого и трудности задания с учетом превышений предельного времени выполнения задания.
Характеристики /(г) апб а могут быть оценены методом максимального правдоподобия с использованием эмпирических данных, представляющих результаты тестирования для испытуемых с заранее определенными уровнями достижений и заданий с заранее известными уровнями трудности.
Параметры к(7* , г, й) определяются непосредственно с помощью эмпирических данных через отношения количеств испытуемых, которые превышают и не превышают соответствующие временные пределы 7* в случае заданного уровня достижений.
Параметры {7* } п, а также вероятности «ошибок» ре1 могут быть определены путем решения задачи оптимизации с критерием С = ^_0 (е1 - втеап)1. Таким образом, параметры временного ограничения выбираются так, чтобы сделать ожидаемую конечную пару состояний цепи Маркова ближе к центру рассматриваемого диапазона уровней достижений модели. Так как фактические диапазоны значений для параметров {7* } ,_0 я известны заранее, можно использовать численный метод решения задачи оптимизации (Кигаузку е7 а1, 2015, No. 8).
Цепь Маркова (см. рис. 1) идентифицируется отдельно для каждого уровня достижений.
Самообучение модели
После определения уровня достижений с заданной точностью С*, а также после каждой попытки выполнить задание, происходит корректировка значений вероятностей элементов т^, соответствующих уже осуществлённым переходам между состояниями модели этого уровня. Их оценки заменяются на увеличенные малые значения т.(1 + 8), где 8 << 1, в то время как остальные элементы столбца у суммарно уменьшаются на значения т.р / (2п + 1), чтобы сохранить общую сумму элементов столбца равной единице (т.е. сохранить матрицу М(Х;) стохастической). Эта коррекция выполняется для всех испытуемых, проходящих тестирование в течение определённого периода времени.
Представленная серия малых поправок для матричных элементов фактически реализует метод самообучения Кохонена (Койопеп, 2001).
Свойства процедуры тестирования
Процедура тестирования прекращается, когда происходит одно из следующих событий:
— значение етПп становится меньше заданного порогового значения (этот случай обычно сокращает время тестирования, так как данное условие может быть выполнено после предъявления нескольких заданий);
— превышено заданное предельное время тестирования;
— задание, соответствующее состоянию хп, выполняется успешно за время, не превышающее Е*п.
В случае непрерывной шкалы измерений представленный подход может быть использован в режиме «микроскопа», где мы на первом этапе получаем приблизительную оценку с использованием довольно грубых интервалов. Затем, когда испытуемый окажется в конце процедуры тестирования, мы разделяем интервал этапа на несколько подынтервалов меньшего размера, затем на следующем этапе повторяем процедуру тестирования, используя новую цепь Маркова, приспособленную для более точной оценки с этими подынтервалами, и так далее. Чем больше число таких этапов, тем точнее оценка.
Как цепи Маркова, так и указанные выше адаптивные переходы остаются скрытыми для испытуемых, которые взаимодействуют с реализованной математической моделью только на уровне получения новых заданий.
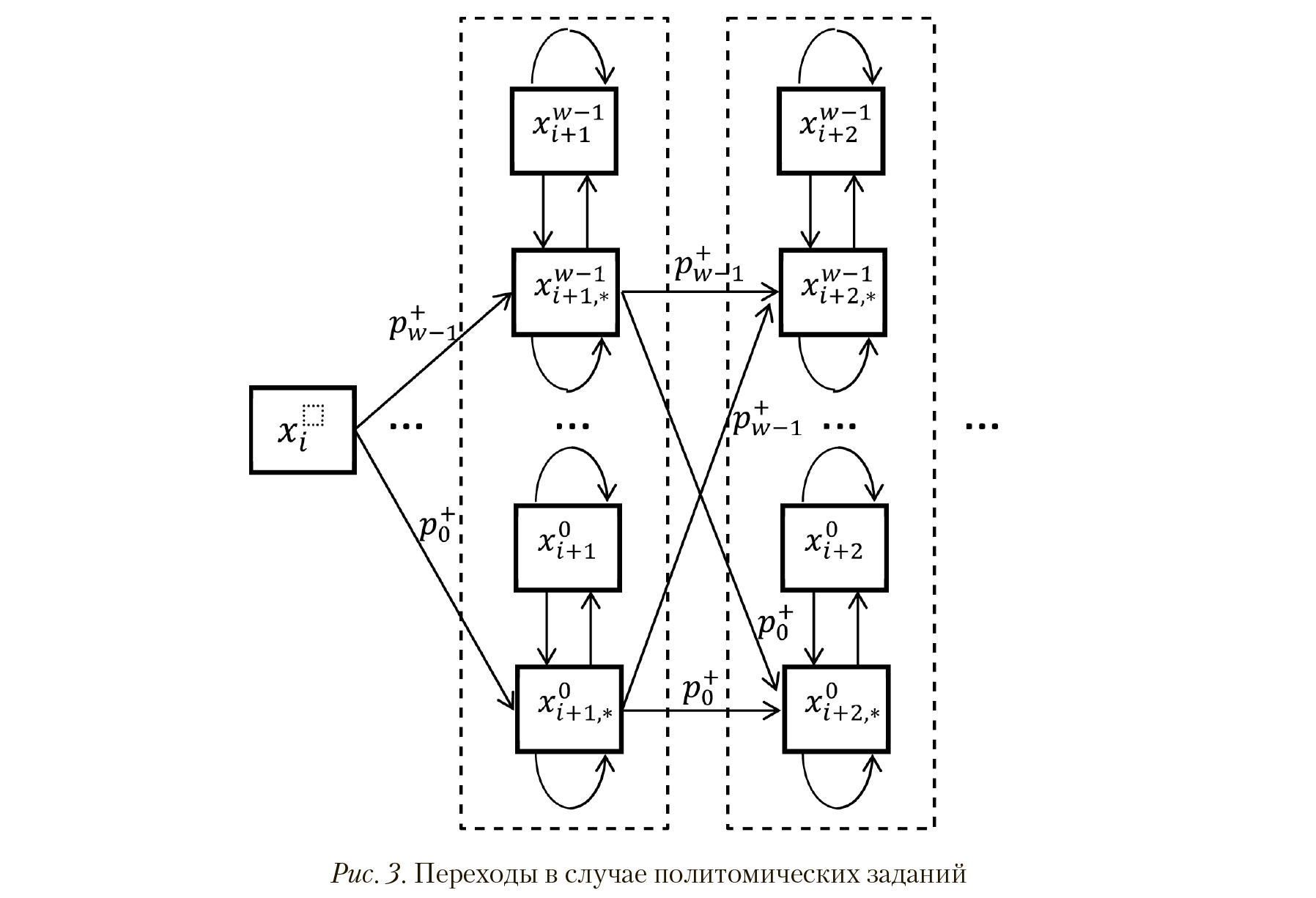
Политомические задания
Рассмотренная модель может быть обобщена на случай политомических заданий. Рассмотрим ® возможных вариантов оценки результатов работы для задания, предъявленного в состоянии х, В этом случае соответствующий переход модели к состоянию х, показанный на рис. 1, заменяется многовариантным переходом, представленным на рис. 3 (каждое состояние х.+1 имеет свою собственную «ловушку»). Предполагается, что вероятности политомических переходов {р+ , ... , р^,_1} пропорциональны эмпирическим частотам переходов, доступным посредством наблюдения.
Трудность заданий
Для оценки трудности заданий разработана «теория двойственности», в которой конструкт испытуемого (например, способность) и шкала трудности заданий рассматриваются как двойственные концепты, заменяющие друг друга. Цепь Маркова, используемая для оценки уровней достижений, может быть применена для вычисления уровней трудности, если рассматриваемые состояния представляют собой уровни достижений, а не уровни трудности заданий, как в предыдущей модели. Задание, которое будет оцениваться, «идёт»
по цепи Маркова и даётся испытуемым, уровень достижений которых соответствует состоянию, в котором исследуемое задание находится в данный момент. Все элементы теории, включая структуру модели, правила перехода, идентификацию модели, а также правила классификации, остаются неизменными.
Задания, оцениваемые с использованием нескольких шкал измерений
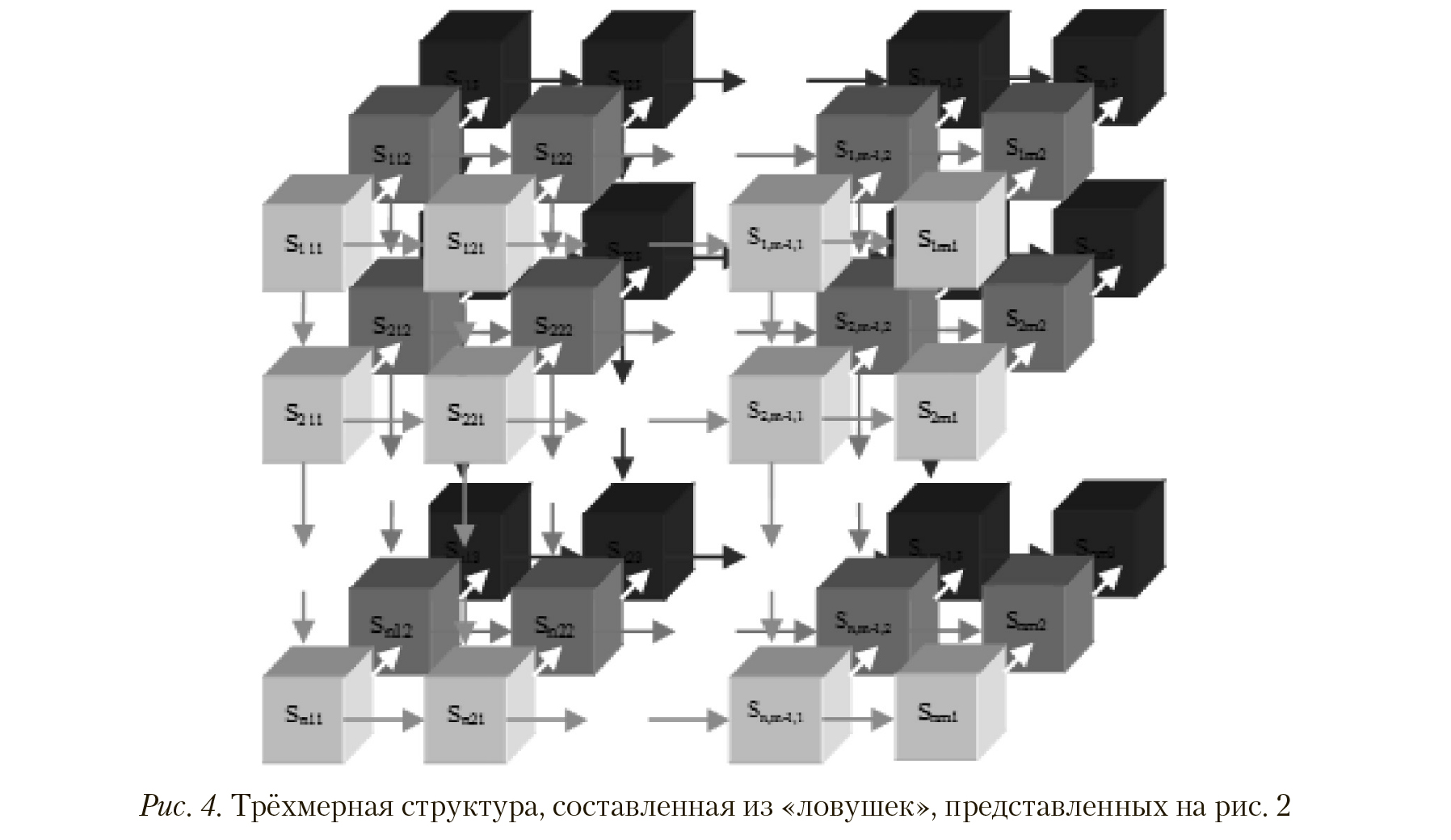
Когда процедура тестирования содержит задания, оцениваемые с использованием нескольких шкал измерений, рассмотренная оценка для каждойшкалыможетбытьвы- полнена независимо с использованием модели, представленной на рис. 1. Полученные результаты могут быть представлены с помощью многомерных структур, составленных из «ловушек», показанных на рис. 2. В качестве примера. трёхмерная структура этого типа приведена на рис. 4 (ее составные элементы представляют собой у помя нутые выше «ловушки»).
Демонстрационная программа
Программа, демонстрирующая особенности рассмотренной модели адаптивного тестирования, доступна по адресу: http://it.mgppu.ru/files/model.zip.
Результаты и выводы
Разработан новый подход к адаптивному тестированию, модель предъявления заданий которого описывается с помощью марковских процессов с дискретными состояниями
и дискретным временем. Этот подход опирается на обобщение модели Г. Раша и имеет существенные преимущества перед адаптивным тестированием на базе современной теории тестирования (ШТ). Его особенностями являются:
1) учёт в модели адаптивного тестирования всей наблюдаемой история выполнения тестовых заданий, включая порядок успешных и неуспешных результатов;
2) учёт времени, затраченного на выполнение тестовых заданий, с помощью временных ограничений в элементах модели, названных «ловушками»;
3) оценки, основанные на прогнозировании будущего поведения испытуемых, которые допускают изменение значений конструктов испытуемого во время процедуры тестирования;
4) возможность самообучения модели, что приводит к улучшению её характеристик в период эксплуатации;
5) использование марковских процессов с дискретным временем вместо аналогичных процессов с непрерывным временем, что облегчает практическое применение рассмотренного подхода;
6) простая процедура идентификация параметров модели на основе доступных результатов наблюдений;
7) связь трудностей предъявляемых заданий с историей прохождения тестов, а не текущими оценками уровней достижений испытуемых;
8) возможности обобщения разработанного подхода на случай политомических заданий и нескольких шкал измерений.
Финансирование
Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 1706-00277).
1 Когда в классической шкале логитов способности примерно равны трудностям, изменение в 0,5 логита в способности дает сдвиг 0,2 в вероятностях. Напротив, в неизменных условиях сдвиг 0,1 в вероятностной мере приводит к изменению в 0,25 логита в измерении способности. Таким образом, оценки весьма чувствительны к ошибкам.