Моделирование латентных изменений c помощью структурных уравнений^*

Модели латентных изменений – один из методов структурного моделирования, позволяющих анализировать временные процессы при наличии малого числа временных срезов. Использование этих моделей особенно актуально в социальных науках и психологии. Они позволяют описывать динамический процесс развития одной или нескольких характеристик в комплексе, а также детерминацию изменений различными инвариантными для этого процесса характеристиками. В первой части статьи рассматриваются различные случаи и разновидности моделей. Во второй части эти модели используются для анализа, проведенного в Лос Анжелесе, конкретного социально-психологического лонгитюдного исследования употребления психоактивных веществ молодежью.

Основные положения и принципы структурного моделирования

Структурное моделирование (СМ), или моделирование структурными уравнениями, по сути дела, всеобъемлющая и необычайно мощная техника многомерного анализа, включает большое количество методов из различных областей статистики. Кратко можно сказать, что структурное моделирование представляет собой развитие многих методов многомерного анализа, а именно: множественная линейная регрессия, дисперсионный анализ, факторный анализ, которые получили здесь естественное развитие и объединение (Митина, 2005; Bentler, 1995).

Основные понятия, с которыми работает структурное моделирование, – это переменные, в психологии – ответы на пункты опросников, характеристики, показатели, выраженность качеств и т. д. Переменные могут быть измеряемыми, наблюдаемыми, их значения определяются непосредственно в результате опроса, отчета или самоотчета, наблюдений, физических, физиологических, социально-демографических измерений. Другой тип переменных – латентные, ненаблюдаемые. Это гипотетические конструкты, которые нельзя измерить непосредственно. Исследователь, строя свою психологическую теорию, предполагает их существование и проявление через измеряемые переменные. Значение этой латентной переменной определяется исходя из заданных в теории структурных уравнений на основании значений измеряемых переменных.

В структурных моделях латентные переменные обозначаются буквой F (factor – фактор), а наблюдаемые V (variable – переменная).

Все переменные, измеряемые и латентные, взаимодействуют друг с другом. Характер этих взаимодействий устанавливается исследователем на этапе формулирования гипотез. Переменные могут детерминировать одна другую (т. е. составлять причинно-следственную пару): детерминирующая переменная называется независимой, а детерминируемая – зависимой. В причинно-следственных парах в качестве зависимых и независимых переменных выступают как латентные, так и наблюдаемые переменные в любом сочетании. То есть и латентные и наблюдаемые переменные могут детерминироваться и латентными и наблюдаемыми переменными. Возможно также, что зависимая переменная, в свою очередь, также может детерминировать какую-либо третью переменную. Другой тип связи между переменными, участвующими в модели, – корреляционный. Переменные каким-то образом связаны друг с другом, но нет оснований говорить, что одна из них является причиной, а другая следствием.

Чтобы модель была полна, правила структурного моделирования предполагают, что для каждой зависимой переменной (латентной или измеряемой), помимо общей части, определяемой весовым вкладом детерминирующих ее известных независимых переменных, есть еще и специфичность, в модели не вычисляемая, но выражаемая латентной переменной E для наблюдаемых зависимых переменных и D – для латентных зависимых переменных. Эти остаточные переменные, являясь латентными и независимыми, также взаимодействуют между собой по всем правилам структурной модели. Как правило, остаточные компоненты не включаются в интерпретацию и выносятся за рамки анализируемой модели. В структурном моделировании бывает достаточно просто указать на них и обозначить их как E (от слова “error” – ошибка). Однако мы склонны придавать им большее значение и интерпретировать их не как ошибку модели, а как специфичность переменной, которую данная модель не учитывает либо в силу заранее известной ограниченности (поскольку любая модель не совершенна), либо в силу недостаточной разработанности. Анализ взаимосвязей между остаточными членами нам представляется полезным и информативным.

Существует два эквивалентных способа задать модель – графически, с помощью диаграммы, или с помощью системы линейных уравнений множественной регрессии и ковариационных соотношений. На структурных диаграммах латентные переменные обозначаются овалами, а наблюдаемые прямоугольниками, причинно-следственная пара соединяется односторонней стрелкой, исходящей из независимой и оканчивающейся на зависимой переменной. Ковариационные связи обозначаются двухсторонними стрелками (рис. 1).

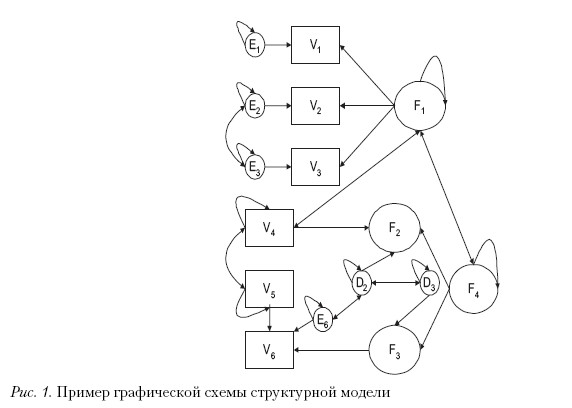
Факт, что переменная X детерминирует переменную Y, на графике обозначаемый односторонней стрелкой, задается следующим структурным уравнением:

Y = aX + EY, где a – это коэффициент детерминации, EY – остаточный член[2].

Значения параметров a и b могут быть определены заранее, исходя, например, из результатов каких-либо предыдущих исследований, данных наблюдений или предполагаются к оценке в ходе анализа модели. В последнем случае эти коэффициенты заменяются звездочками.

В структурном моделировании задаются или оцениваются ковариации (корреляции) только независимых переменных. Ковариации зависимых переменных вычисляются исходя из симметричности и линейности этой функции: (aX+bY,Z) = (Z,aX+bY) = a(X,Z) + b(Y,Z).

Ковариация переменной с самой собой есть вариация и является ее мерой разброса. На диаграммах вариации обозначаются круговой стрелкой, исходящей и заканчивающейся на самой переменной, и чаще всего просто упоминаются, а на самом рисунке опускаются. Вариации, как и ковариации и коэффициенты детерминации, могут быть заранее известными исходя из теоретических соображений или предыдущих исследований, а могут оцениваться в ходе анализа модели. Вариации остаточных членов E и D, являющихся независимыми латентными конструктами, считаются заранее неизвестными и обозначаются звездочками, а вот их коэффициенты детерминаций на исследуемые зависимые переменные для задания масштаба полагаются равными 1. Ниже представлена эквивалентная структурной схеме система уравнений.

Следующие два этапа в определенном смысле напоминают этапы регрессионного анализа. Вначале с помощью минимизирующей процедуры (чаще всего метода наименьших квадратов) вычисляются оценки для регрессионных коэффициентов, вариаций и ковариаций независимых переменных, а потом с помощью статистических критериев определяется значимость вычисленных параметров и интегральный показатель, позволяющий определить, насколько теоретическая модель, заданная формулами, в целом соответствует экспериментальным данным. Таких показателей несколько:

• отношение c2 к числу степеней свободы df. Оптимально, чтобы этот показатель не был больше 2.
• CFI (Comparative Fit Index) – сравнительный критерий согласия, лежащий в пределах от 0 до 1. Если CFI больше 0,9, значит, модель согласована.
• RMSEA (root mean-square error of approximation) – квадратичная усредненная ошибка аппроксимации. Этот показатель также лежит в пределах от 0 до 1. Однако для принятия нулевой гипотезы его значение не должно превышать 0,05.

Как правило, исследователь принимает решение о согласованности модели исходя из общей совокупности значений указанных показателей. Если один из показателей дает «хорошее» значение, а остальные не очень сильно отклоняются от критериального интервала, можно принимать гипотезу о согласованности.

Моделирование латентных изменений

Моделирование латентных изменений наряду с конфирматорным факторным анализом, анализом путей входит в арсенал методов структурного моделирования.

В англоязычной литературе этот набор техник называется «Latent Growth Modeling», что дословно можно перевести как моделирование латентного роста. Однако мы предпочитаем употреблять именно слово «изменения», так как динамика может происходить не только в сторону роста, но и падения, либо иметь какую-то нелинейную форму.

Этот метод применяется наиболее часто для анализа повторяющихся измерений, для данных, полученных в ходе лонгитюдных исследований (Duncan et al., 1999). Однако он также может быть использован и в том случае, если выбрать какой-либо независимый параметр и получать данные (повторять измерения), последовательно (упорядоченно) изменяя значения независимого параметра. Очевидно, что при лонгитюде этим независимым параметром является время, а естественный временной ход соответствует последовательному изменению значений этого независимого параметра.

Для простоты рассмотрим в начале моделирование латентного линейного роста. Далее все рассуждения могут быть распространены на более общий случай латентных изменений (как монотонных, так и немонотонных).

Линейный рост можно представить с помощью уравнения Y=aX+b (рис. 2). X – это независимая переменная, Y – это линейно зависимая от X переменной. Параметр a соответствует углу наклона прямой, а параметр b – точке пересечения этой прямой с осью OY (т. е. уровню, на который эта наклонная прямая приподнята (если b > 0) или опущена (если b < 0) над осью OX).

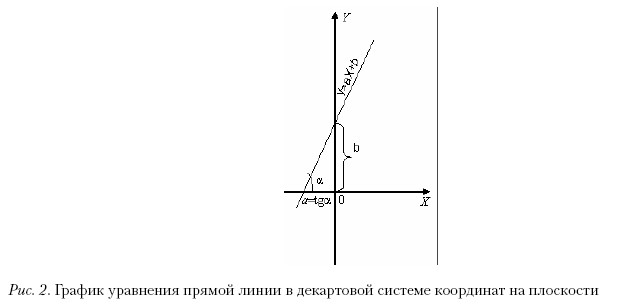
Если теперь предположим, что в ходе эксперимента были зафиксированы две переменные X и Y, и было сделано n наблюдений, то есть получено n пар значений (X_i Y_i), то известная задача линейной регрессии заключается в нахождении таких значений a и b, чтобы прямая Y=aX+b алгебраически и статистически соответствовала экспериментальным данным (Тюрин, Макаров, 1998).

Эта же идея используется и при моделировании латентного линейного роста. В случае когда имеется некоторое количество повторяющихся измерений Y_i (I = 0,1, …, n – временные этапы), необходимо выявить меньшее количество латентных факторов (в линейном случае два), позволяющих описывать всю модель без существенной потери информации.

На рис. 3 изображена схема взаимосвязи латентных и наблюдаемых переменных, используемая для моделирования латентного линейного роста. Y₁, Y₂, Y₃ – это измерения какой-либо характеристики, выполненные при последовательно возрастающих значениях независимого параметра. В данной модели латентные факторы отмечены F₀ и F₁ и позволяют моделировать характер изменений. Односторонние стрелки соответствуют связям детерминации (латентные переменные детерминируют наблюдаемые переменные). Числа, стоящие рядом со стрелками, обозначают факторные нагрузки того или иного фактора на соответствующие переменные.

Как видим из рис. 3 и соответствующей системы уравнений, факторные нагрузки по фактору F₀ одинаковы для всех наблюдаемых переменных, а по фактору F₁ изменяются с каждым следующим шагом на единицу, т. е. пропорционально n (номеру измерения). Таким образом, если проводить аналогию с уравнением линейной регрессии, фактор F₀ соответствует константе, а фактор F₁ – коэффициенту наклона.

Однако существенное различие между линейной регрессией и латентным моделированием линейного роста заключается в составе требуемых для анализа данных.

В первом случае необходимо большое количество пар наблюдений над различными объектами по зависимой Y и независимой X переменным. Во втором случае необходимо производить наблюдения (измерения зависимой переменной Y) над одними и теми же объектами при различных фиксированных уровнях (значениях) независимого параметра (переменной X). В этом смысле дизайн эксперимента аналогичен дисперсионному анализу, при проведении которого также необходимо измерять зависимый показатель у всех объектов при разных уровнях анализируемого фактора (Гусев, 2000). Если в случае линейной регрессии множество различных значений X_i должно быть большим, чтобы гарантировать достоверность результатов, то в случае моделирования латентного линейного роста различных уровней может быть немного (например, трех вполне достаточно), однако такая возможность ставит перед необходимостью проведения измерений зависимой переменной у всех элементов выборки при каждом значении независимого параметра.

Моделирование латентных изменений позволяет определить не только общие для всей выборки показатели – наклон и константу (макроуровень), но и установить, от чего эти коэффициенты могут зависеть у каждого конкретного объекта наблюдений (индивида) (микроуровень).

На рис. 4 представлены различные виды линейных графиков. С помощью линейной регрессии можем вычислить одну «усредненную» прямую, у которой коэффициенты a и b являются усредненными значениями коэффициентов a_i и b_i для каждого индивида в отдельности. Структурное моделирование позволяет выявлять латентную линейную зависимость (т. е. строить линейный график) для каждого испытуемого, соотносить индивидуальные зависимости друг с другом, определять характер разброса, причины выявленных различий.

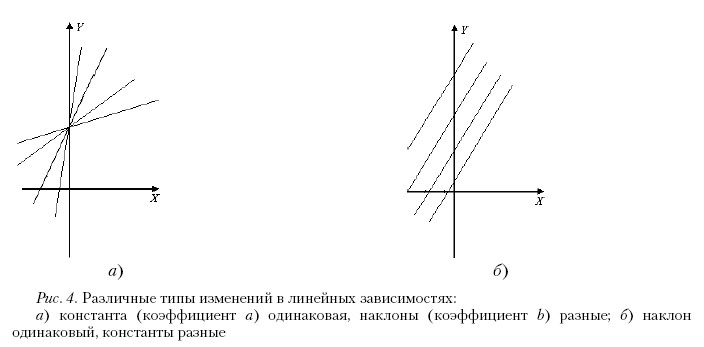
Таким образом, можно сказать, что латентное моделирование линейного роста в определенной степени интегрирует идеи линейного регрессионного анализа, факторного и дисперсионного анализа и позволяет использовать преимущества всех этих методов одновременно.

Моделирование латентных нелинейных изменений

Представленная модель латентных изменений для линейного случая легко может быть распространена и на более сложный случай, предполагающий нелинейные изменения одной или (и) совокупности характеристик. Ниже разберем различные примеры.

Простые одномерные модели. Моделируются нелинейные изменения одной характеристики (рис. 5).

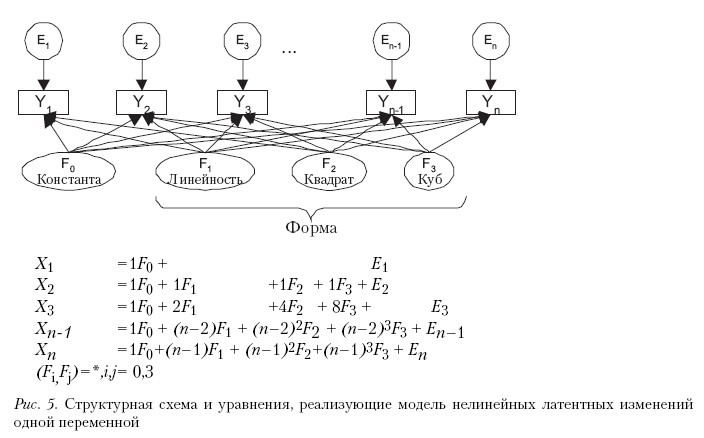
Как видно из соответствующей системы уравнений, факторные нагрузки по фактору F₀, соответствующему константе, одинаковы для всех наблюдаемых характеристик, по фактору F₁ (линейный член) изменяются с каждым следующим шагом на единицу, т. е. пропорционально номеру измерения, по фактору F₂ (квадрат) пропорционально квадрату номера измерения, по фактору F₃ (куб) пропорционально кубу номера измерения и т.д.

Кроме того, в общем случае допускается, что латентные факторы могут быть взаимосвязаны между собой, поэтому последней строчкой добавлено ковариационное соотношение всех факторов между собой. Графически им должны соответствовать двусторонние стрелки, но, чтобы избежать нагромождений, на рис. 5 они опущены.

Число латентных факторов может быть сколь угодно большим. Однако рекомендуется соблюдать принцип разумной простоты. Если модель хорошо удовлетворяет экспериментальным данным полиномом степени n, не имеет смысла рассматривать модель более высокой степени. Факторы F₁, F₂, F₃ … задают форму кривой. Если же возникает необходимость смоделировать любую другую нелинейную зависимость j(X), коэффициенты перед фактором, соответствующим одночленной функции j, должны изменяться как j(n), а многочленная моделируется как линейная комбинация одночленов.

Многопеременные модели

Моделируются нелинейные изменения нескольких характеристик одновременно. На рис. 6 представлена модель для трех характеристик, каждая из которых изменяется линейно. Однако модель легко может легко быть распространена на случай, во-первых, большего числа наблюдаемых характеристик, а во-вторых, на случай когда они все (или некоторые из них) изменяются нелинейно.

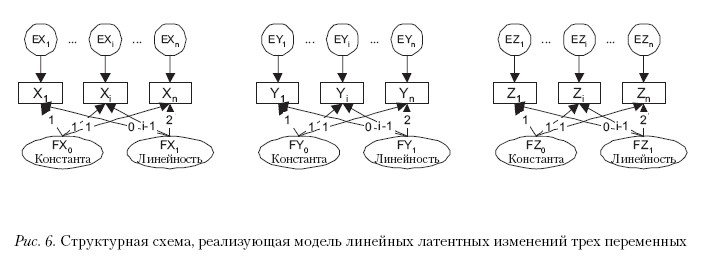
При этом возможны различные взаимосвязи латентных факторов друг с другом.

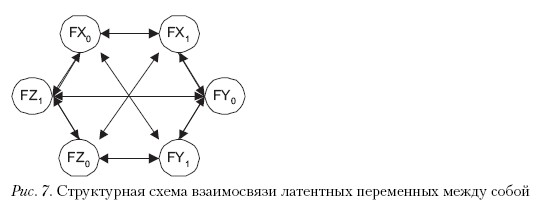
Ассоциативная модель предполагает, что все латентные факторы могут коррелировать друг с другом (рис. 7). Система уравнений дополняется ковариационными соотношениями всех факторов со всеми.

В модели латентных конструктов латентных изменений предполагается существование факторов второго порядка: общая константа и общая линейность (рис. 8). Для экономии места на рис. 8 верхняя часть модели – зависимость наблюдаемых характеристик от латентных факторов первого порядка – опущена, но она в точности сохраняется.

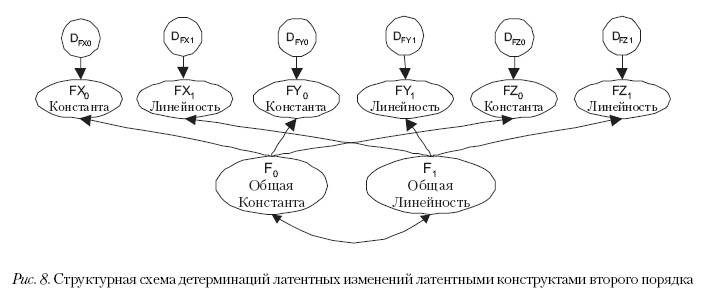
Поэтому к уравнениям, описывающим модель рис. 6, добавляются следующие уравнения:

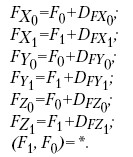
В случае когда предполагается, что измеряемые характеристики более тесно связаны друг с другом в каждый момент измерения, используется модель латентных изменений латентных конструктов (рис. 9).

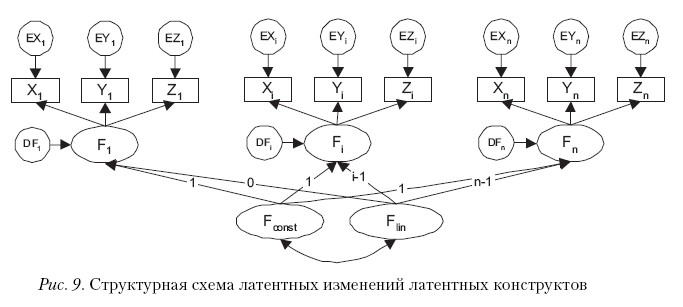
Соответствующая система уравнений имеет вид:

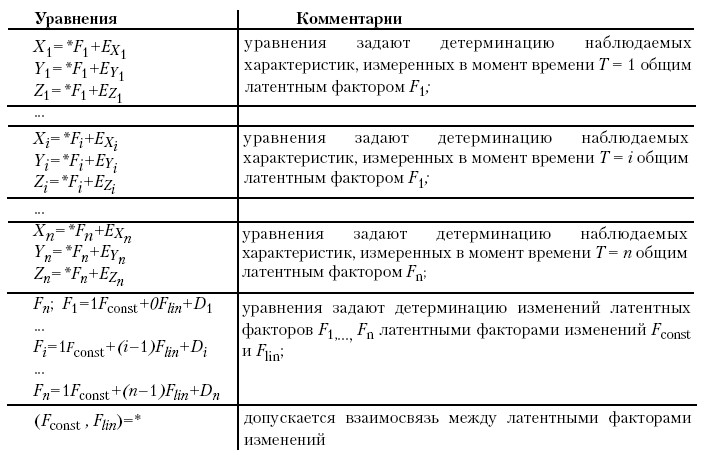
Моделирование детерминаций фактором изменений внешними параметрами. Модели латентных изменений позволяют не только установить детерминацию изменений латентными факторами изменений, но также проверить гипотезы о детерминации этих факторов какими-либо внешними коррелятами: наблюдаемыми характеристиками или факторами, инвариантными в течение всего процесса (рис. 10). Рассмотрим лишь простейший случай – одна переменная, линейные изменения. Однако все рассуждения с равным успехом можно применять в более сложных случаях.

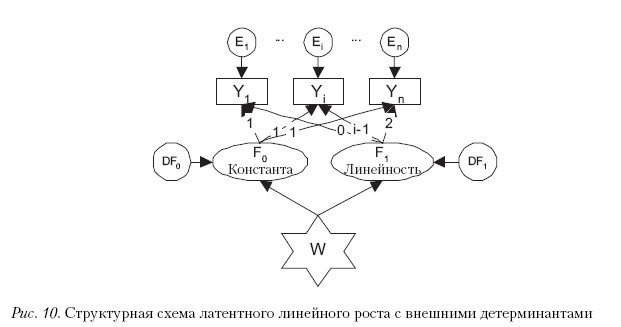
Ковариационное соотношение между факторами, используемое в рис. 3, заменяется детерминационными уравнениями

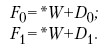
W – инвариантный параметр. Например, нас интересует, как изменяется со временем (год от года) успеваемость ученика по какому-либо предмету (характеристика Y), а W – это его пол.

Моделирование дисконтинуальных изменений. Предлагаемая методология может быть использована для анализа процесса, предполагающего разрыв в какой-либо момент времени. Таким образом мы можем проследить и промоделировать не только непрерывные процессы (рис. 11).

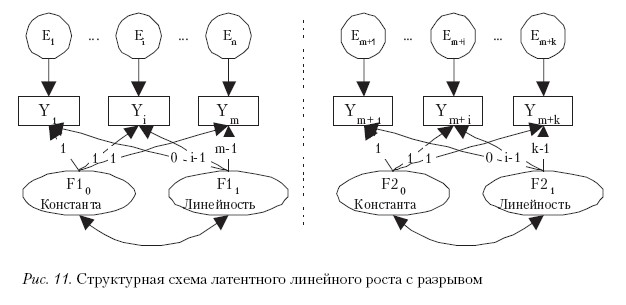
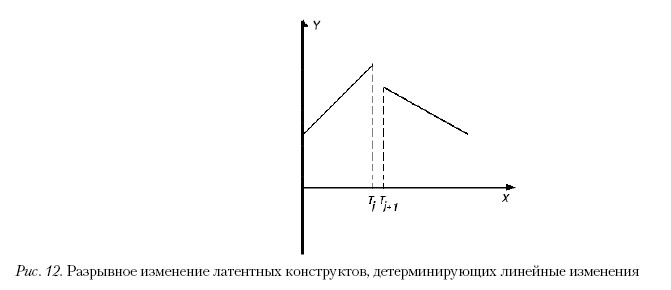
Согласно модели в момент времени m произошло качественное изменение параметров. Эти изменения могут быть различны. Например, на обоих этапах характер детерминации сохранился: до момента разрыва и после него изменения носили линейный характер, однако значения факторов линейности и константности значимо отличаются. В терминах графиков ситуация отражена на рис. 12. Возможно также не только изменение значений факторов, но и их число (например, переход от линейных изменений к нелинейным).

Пример использования моделей латентных изменений в конкретном социально-психологическом исследовании

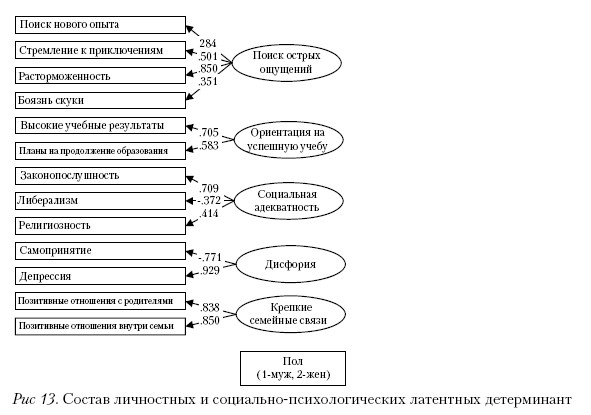
Продемонстрируем применение указанных выше моделей. Данные были получены в ходе масштабного лонгитюдного исследования употребления психоактивных веществ (ПАВ), проводимого в Калифорнийском университете Лос-Анжелеса под руководством П. Бентлера и М. Ньюкомба[3]. 332 испытуемых (94 мужчины и 238 женщин) наблюдались в течение 17 лет с 1976 года по 1993. Было сделано шесть замеров. Возраст респондентов во время проведения каждого из них составлял 12–13, 16–17, 20–21, 24–25, 28–29 и 28–29 лет соответственно. Каждый замер – это широкомасштабный опрос, включавший социально-демографические вопросы, личностные опросники, методики коммуникативного характера, вопросы, связанные с семейной обстановкой, друзьями, исследовалась динамика отношения к психоактивным веществам: частота употребления алкоголя, сигарет и наркотиков. На рис. 13 представлены основные социально-психологические переменные (латентные в овалах, наблюдаемые в прямоугольниках), определенные при первом опросе. В задачу исследования входило выявить характер динамики употребления различных ПАВ с возрастом; влияние социально-демографических и психологических переменных, проявившихся в раннем подростковом возрасте на последующее употребление ПАВ.

На первом этапе анализа данных была построена трехпеременная ассоциативная модель с социально-психологическими и демографическими детерминантами (рис. 14). Статистические показатели модели свидетельствуют о высокой степени соответствия экспериментальным данным.

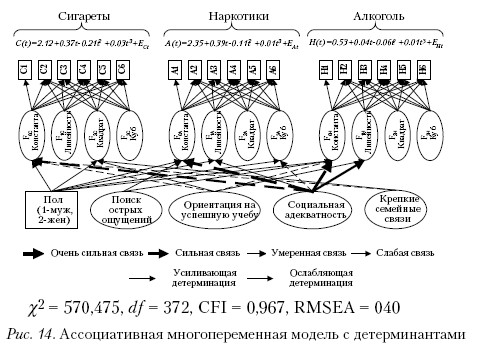
В задачу данной статьи не входит подробная интерпретация данной схемы, она будет сделана в публикациях, посвященных именно факторам риска и защиты употребления ПАВ, однако здесь мы считаем необходимым кратко проиллюстрировать возможные направления чтения подобных схем.

Во-первых, кривые роста для всех трех видов ПАВ выглядят аналогично: это возрастающие кубические кривые с отрицательным коэффициентом при квадратичном члене. То есть хотя в течение жизни и возможны некоторые спады в употреблении тех или иных ПАВ, доминирующей тенденцией является все-таки рост. Однако главным фактором употребления ПАВ является актуализированность этой привычки в младшем подростковом возрасте. В уравнениях – это константа. И особенно велика она в случаях употребления сигарет и алкоголя. При этом у девочек в этот период тяга к ПАВ проявляется сильнее, чем у мальчиков (константа положительно детерминирована полом). В младшем подростковом возрасте девочки в большей степени социально активны, а употребление ПАВ, по их мнению, способствует повышению их статуса как среди одноклассников, так и среди более взрослых подростков, с которыми они предпочитают проводить досуг. Это и является причиной, что в возрасте 12–13 лет именно девочки более часто употребляют ПАВ, нежели мальчики.

Существенным этот рост на фоне изначальной предрасположенности не является. В более старшем возрасте социальные, да и внутренние установки (молодые женщины в большей степени следят за своим здоровьем) приводят к обратному эффекту: так, например, при употреблении алкоголя линейный коэффициент оказывается выше для респондентов-мужчин.

К факторам риска употребления ПАВ следует отнести стремление к острым ощущениям, к факторам защиты – ориентацию на академическую успеваемость и крепкие семейные связи. Социальная адекватность, являясь фактором защиты на ранних этапах, впоследствии может, трансформировавшись в близкую социально-психологическую диспозицию социальной конформности, оказывать уже неблагоприятное влияние (см. положительную детерминацию линейного коэффициента употребления алкоголя и наркотиков и отрицательную константы во всех трех случаях). Конформный человек может употреблять ПАВ просто за компанию под влиянием сверстников.

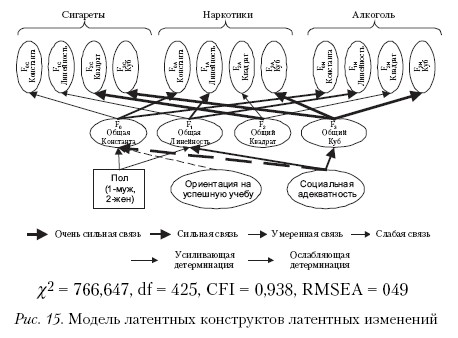
Данная схема свидетельствует о наличии общих латентных факторов второго порядка, определяющих характер изменений. То есть тенденции в употреблении всех трех видов ПАВ схожи. Данная схема вполне согласуется с предыдущей (представленной на рис. 14). На ранних подростковых этапах девочки в большей степени склонны употреблять ПАВ, а в дальнейшем в большей степени этому риску подвергаются юноши и молодые мужчины. К факторам защиты от употребления ПАВ однозначно относится ориентация на успешную учебу, социальная адекватность, играя защитную роль, иногда может оказаться и неблагоприятным фактором.

Следующая модель, рассмотренная нами, отражала динамику обобщенной латентной переменной, названной «употребление ПАВ». Непосредственно ее измерить нельзя, она латентная, но именно эта характеристика, по нашему предположению, детерминирует курение, употребление алкоголя и наркотиков, проявляемые непосредственно. Как уже было сказано выше, модель латентных изменений латентных переменных позволяет выявить, как латентная характеристика изменяется во времени, и что является детерминантами процесса. На рис. 16 представлена структурная схема. Согласно модели, которая очень хорошо согласована с экспериментальными данными, можно видеть, что изменения описываются кубической кривой с отрицательным коэффициентом при квадратичном члене. Факторы риска и защиты такие же, как и в предыдущих случаях для отдельных видов ПАВ. Эти факты можно интерпретировать как устойчивость и надежность полученных решений как в этом, так и в двух предыдущих случаях: характер динамики везде один и тот же, факторы риска и защиты употребления ПАВ также сохраняются.

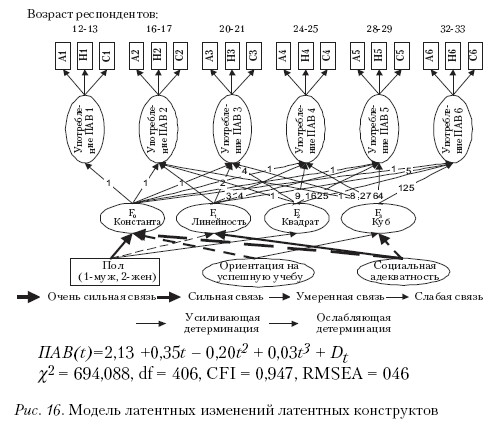
Последняя модель предполагает существование точки разрыва, т. е. наличие момента, в котором анализируемый процесс существенным образом меняет свои характеристики.

В качестве такой точки мы выбрали возраст 20–21 год. С содержательной точки зрения этот выбор обосновывается тем, что в США – это возраст совершеннолетия. Достигнув этого возраста, молодые американцы получают право курить сигареты и употреблять спиртные напитки официально. Мы предположили, что легализация употребления определенных видов ПАВ должна отразиться на показателях процесса. Таким образом, мы выделили два временных промежутка: до и после наступления совершеннолетия, и построили модели линейных латентных изменений с детерминантами. Характер детерминаций подтверждает результаты, полученные на предыдущих моделях. А именно: девочки в большей степени, нежели мальчики, склонны употреблять ПАВ в младшем подростковом возрасте, однако скорость вовлечения в употребление ПАВ у мальчиков выше.

Ориентация на академическую успеваемость во всех случаях является фактором риска.

Фактор стремления к новым ощущениям амбивалентен: его выраженность приводит к тому, что на этапе ранней молодости сразу после наступления совершеннолетия молодые американцы в большей степени склонны употреблять ПАВ, однако затем они, по всей видимости, находят иные способы удовлетворения этой потребности (спорт, экстремальная деятельность, путешествия) и тем самым ослабляют употребление ПАВ.

Социальная адекватность на первом этапе амбивалентна, а на втором однозначно является фактором защиты.

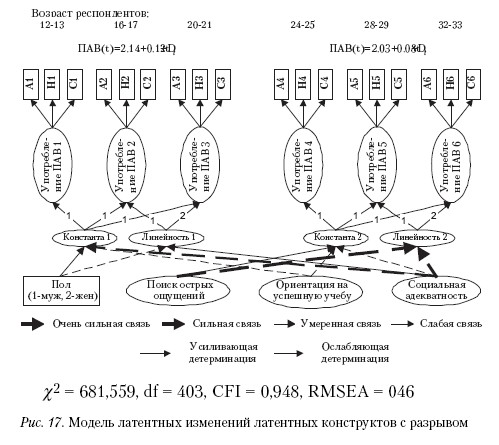
В заключение отметим, что модели латентных изменений дают богатый материал для интерпретаций и безусловно должны соотноситься с содержательной областью. То есть выбор окончательной модели должен быть сделан психологом исходя из теоретических соображений, а статистические показатели могут играть лишь вспомогательную роль. Рассмотренный пример конкретного эмпирического исследования, со статистической точки зрения, допускает принятие любой из приведенных моделей. Чтобы ответить на вопрос об окончательном выборе той или иной модели, необходимы теоретические соображения, связанные с изучением употребления ПАВ, факторами риска и защиты этого употребления. Вполне возможно, что в определенных случаях могут быть использованы различные модели, так как они не противоречат, а дополняют друг друга. Но это тема другой статьи.

---

1. Гусев А. Н. Дисперсионный анализ в экспериментальной психологии. М.: УМК «Психология», 2000.
2. Митина О. В. Структурное моделирование: состояние и перспективы // Ученые записки кафедры общей психологии факультета психологии МГУ. М.: Смысл, 2005.
3. Тюрин Ю. Н., Макаров А. А. Анализ данных на компьютере. М.: Инфра, 1997.
4. Bentler P. M. EQS, Structural Equations, Program Manual. CA, Encino: Multivariate Software, Inc, 1995.
5. Duncan T., Duncan S., Strycker L., Li F., Alpert A. An Introduction to Latent Variable Growth Curve Modeling. London. 1999.