Методические вопросы использования факторного анализа на примере спектральных показателей сердечного ритма

Настоящая статья посвящена рассмотрению ряда методических вопросов, касающихся использования факторного анализа для оценки спектральных показателей сердечного ритма, а именно: допущения многомерности нормального распределения исследуемых признаков, целесообразности применения факторной модели анализа к исходным данным, процедуры отбора общих факторов, значимости полученного факторного решения. В проведенном исследовании были использованы переменные, характеризовавшиеся нарушением нормального распределения, переменные, преобразованные к нормальному распределению, а также матрицы корреляции Пирсона и Спирмена, модельные данные. В процессе проведенного факторного анализа (метод главных компонент, Varimax-вращение) нами проанализированы как возможности, так и ограничения различных статистических критериев и процедур; рассмотрена природа выделенных общих факторов и возможность использования корреляций Спирмена при нарушениях нормальности распределения.

Факторный анализ относится к методам многомерного статистического анализа и широко используется для снижения размерности анализируемого пространства признаков, отбора наиболее информативных показателей и классификации объектов. В основе факторного анализа лежит общая базовая идея, согласно которой структура связей между многочисленными анализируемыми переменными может быть объяснена их зависимостью от меньшего числа непосредственно неизмеряемых («скрытых», «латентных», «гипотетических») общих факторов (Айвазян и др., 1989). Основной предпосылкой для итогового снижения размерности пространства анализируемых признаков служит взаимная коррелированность исходных переменных, а исходными данными для анализа выступает матрица их парных коэффициентов корреляции (или ковариации).

Факторный анализ можно использовать не только как метод сжатия информации, но и как основу классификации, заменяя исходные признаки факторами; в данном случае классификация объектов заключается в получении факторных оценок для каждого из них и последующей визуальной или аналитической группировке этих объектов в факторном пространстве, что позволяет перейти от типологизации по большому числу исходных признаков к построению классификации на основе значительно меньшего числа факторов, с более ясным аналитическим описанием и графическим представлением данных.

Идея использования факторного анализа для классификации функциональных состояний человека на основе спектра сердечного ритма была реализована в ряде психофизиологических исследований Н. Н. Даниловой (Данилова, 1995, 1998; Данилова, Астафьев, 1999). В этих исследованиях основу факторной модели составили три показателя спектра мощности сердечного ритма, которые должны были характеризовать дыхательные (0.12÷0.16 Гц), сосудистые (0.06÷0.10 Гц) и метаболические (0.02÷0.04 Гц) воздействия на сердечный ритм (Данилова, Астафьев, 1999). Поскольку границы частотных диапазонов указанных показателей могут сильно колебаться, для классификации функциональных состояний было предложено использовать метод факторного анализа. Для этого были рассчитаны показатели мощности спектра сердечного ритма в 25 частотных диапазонах, которые были сгруппированы в 10 переменных: 0.005÷0.02 и 0.02÷0.04 Гц (метаболическая модуляция); 0.04÷0.06, 0.06÷0.08 и 0.06÷0.1 Гц (сосудистая модуляция); 0.1÷0.12, 0.12÷0.14, 0.14÷0.16, 0.16÷0.3 и 0.3÷0.5 Гц (дыхательная модуляция) (Данилова, 1995). В соответствии с полученной матрицей взаимных корреляций 10 переменных далее было выделено три общих фактора, которые интерпретировались как метаболические, сосудистые и дыхательные модуляции сердечного ритма. Оценки по общим факторам служили основой для типологизации функциональных состояний обследуемых в факторном пространстве вегетативных влияний на сердечный ритм.

В своем исследовании мы решили рассмотреть различные методические вопросы приложения факторного анализа к спектральным показателям сердечного ритма, включая допущение о многомерности нормального распределения исследуемых показателей, проверку целесообразности применения факторной модели анализа к исходным данным, процедуры отбора общих факторов, оценку значимости полученного факторного решения. Отдельного внимания, с нашей точки зрения, заслуживает вопрос о возможности содержательной (физиологической) интерпретации природы полученных общих факторов. Отметим, что спектральные показатели сердечного ритма находят широкое применение в современных психофизиологических исследованиях.

Методика

В эксперименте приняли участие 734 оператора АЭС, которые проходили обследования в Лаборатории психофизиологического обеспечения Нововоронежского учебнотренировочного центра подготовки специалистов для АЭС (ЛПФО НВУТЦ). У всех обследуемых отсутствовали нарушения здоровья (мужчины, средний возраст 29.87 лет, стандартное отклонение 7.17 лет). Регистрация сердечного ритма выполнялась в спокойном состоянии в положении сидя в течение 10 минут.

Для записи QRS-комплексов нормальных синусовых кардиоциклов ЭКГ и последующего выделения из них R-R интервалов (в миллисекундах) использовался 3-канальный программно-аппаратурный комплекс «Варикард-1.51» (частота дискретизации 500 Гц). Хранение, редактирование R-R интервалов (коррекция артефактов, экстрасистол на ритмограмме) и расчет показателей спектра мощности сердечного ритма выполнялись с применением компьютерной программы «МАВР.DBase-HRV», разработанной в ЛПФО НВУТЦ («Delphi-5», «Access-2000»). Перед расчетом спектральных показателей из временного ряда сердечного ритма удалялся линейный тренд, рассчитанный с помощью метода наименьших квадратов. Для соблюдения требования об эквидистантности временного ряда (равные промежутки времени измерения переменной) границы частотных диапазонов спектра кардиоинтервалов корректировались по следующей формуле:

FD = FD×M, где FD – исходная граница частотного диапазона, FD – скорректированная, M_NN – среднее значение продолжительности R-R интервалов в выборке (в секундах) (Машин, 2002). Мощность спектральной плотности сердечного ритма (в мсек²) рассчитывалась с помощью быстрого преобразования Фурье со спектральным окном Хэмминга по стационарным «скользящим» выборкам объемом 256 и шагом 10 R-R интервалов. Для проверки выборок на стационарность применялся непараметрический метод ВяльдаВольфовитца (Зырянов и др., 1990). Весь спектр (0.0÷0.5 Гц) был поделен на 25 частотных областей D₁÷D₂₅ (длительностью 0.02 Гц), по которым были получены усредненные по каждому обследуемому показатели мощности спектральной плотности сердечного ритма (объем выборки n = 734), которые послужили исходными данными для проведения факторного анализа.

Для оценки нормальности распределения данных, расчета матриц корреляций и выполнения факторного анализа использовалась статистическая программа «Statistica 6.0». Расчет статистических критериев для проверки целесообразности применения факторной модели анализа, значимости полученного факторного решения и конгруэнтности различных факторных структур был выполнен с помощью специально разработанной программы «МАВР-FA».

Результаты исследования и их обсуждение

Перед началом выполнения факторного анализа рассмотрим допущение о многомерном нормальном распределении исходных переменных. Ряд авторов утверждают, что для построения линейных факторных моделей переменные должны быть многомерно нормально распределены (Харман, 1972; Rencher, 2002). Из этого как минимум следует, что каждый из исходных показателей мощности спектра сердечного ритма должен быть распределен по нормальному закону и между исследуемыми показателями должны существовать линейные связи. Существует также точка зрения, что предположение о многомерной нормальности может играть существенную роль лишь на стадии проверки адекватности факторных моделей, поскольку статистические критерии согласия чувствительны к этому допущению (Справочник по прикладной статистике, 1990). Наконец, ряд исследователей полагают, что факторная модель не требует выполнения предположения о многомерной нормальности закона распределения параметров, хотя отмечают, что последствия нарушения этого допущения до сих пор остаются не вполне ясными (Ким и др., 1989).

Визуальный анализ гистограмм полученных нами данных указывал на выраженные нарушения нормального распределения показателей спектра в 25 частотных областях. Статистический анализ дополнительно позволил установить высокие положительные значения коэффициентов асимметрии (2.28÷10.54) и эксцесса (7.42÷165.69). Напомним, что для нормального распределения коэффициент асимметрии равен 0, а коэффициент эксцесса 3. Для преобразования распределений показателей к нормальному виду были использованы формулы, которые приведены в табл. 1. Гипотеза о нормальности распределений показателей проверялась с помощью критерия Шапиро-Уилка. Поскольку для преобразованных распределений частотных диапазонов D₁₆÷D₂₅ нарушения нормальности сохранялись (p<0.004), они были дополнительно сгруппированы в две переменные: T = D+D+D+D+D (0.30÷0.40 Гц) и T = D+D+D+D+D (0.40÷0.50 Гц). После этого мы получили 17 переменных (V₁÷V₁₇), для которых, согласно критерию Шапиро-Уилка (табл. 1), принималась гипотеза о нормальности распределения (p=0.062÷0.552).

Таблица 1. Формулы приведения переменных к нормальному виду (ln – натуральный логарифм) и значения уровня значимости критерия нормальности распределения Шапиро-Уилка (p).

Примеч.: T = D+D+D+D+D, T = D+D+D+D+D

Для проверки линейной связи между переменными использовались диаграммы рассеивания. Поскольку распределения переменных отвечали нормальному закону (Кендалл, Стьюарт, 1973), мы могли оценить значимость парных коэффициентов корреляции Пирсона, которые служат мерой линейной зависимости между переменными (Хальд, 1956). Для этого рассчитывался критерий:

 , где r – коэффициент корреляции, n – объем выборки (Справочник по прикладной статистике, 1990).

Величина t-критерия (распределенного по закону Стьюдента с n–2 степенями свободы, df) изменялась в диапазоне 8.044÷63.468, что позволяло принять гипотезу о значимости коэффициентов корреляции на уровне p = 0.000. Но поскольку значимость t-критерия могла быть достигнута также за счет большой выборки данных, то для подтверждения вывода о линейной связи между переменными мы дополнительно использовали визуальный анализ диаграмм рассеивания.

Для проверки последствий нарушения допущения о многомерном нормальном распределении исходных данных мы также включили в анализ не преобразованные к нормальному виду переменные D¸D, T и T. Это позволило сформировать для факторного анализа две матрицы параметрических коэффициентов корреляции Пирсона: матрицу А (парные корреляции преобразованных переменных V₁¸V₁₇) и матрицу B (парные корреляции непреобразованных переменных D¸D, T, T). Кроме того, была рассчитана матрица непараметрических коэффициентов корреляции Спирмена для непреобразованных переменных D¸D, T, T (матрица С). Для всех трех матриц корреляций (порядок матриц 17´17) был выполнен факторный анализ.

Перед выполнением факторного анализа по корреляционным матрицам необходимо провести проверку целесообразности использования факторной модели для исследования показателей спектра сердечного ритма. Итак, поскольку факторный анализ относится к той ветви многомерного статистического анализа, которая исследует внутреннюю структуру матриц корреляций (Лоули, Максвелл, 1967), в самом начале необходимо убедиться в наличии значимых корреляционных зависимостей между переменными с помощью критерия сферичности Бартлетта-Уилкса и критерия адекватности выборки Кайзера (measure of sampling adequacy – MSA). Ранее мы проверили значимость каждого парного коэффициента корреляции матрицы А с помощью t -критерия. Для оценки значимости всей корреляционной матрицы Бартлетт предложил критерий, усовершенствованный Уилксом (Rencher, 2002; Иберла, 1980):

, где n – объем выборки, m – число переменных, l n – натуральный логарифм, |R| – определитель матрицы, df = m(m–1)/2.

С помощью критерия Бартлетта-Уилкса проверяется гипотеза о единичной матрице, в которой все элементы главной диагонали равны 1, а все остальные – 0. Данный критерий основан на преобразовании определителя матрицы в статистику χ², при этом если корреляция между переменными будет слабой, то значения |R| будут близки к 1 (снижение χ²), а если 2 или более переменных будут значительно коррелировать друг с другом, то значения |R| будут стремиться к 0 (рост χ²).

Для наших данных были получены следующие значения критерия Бартлетта-Уилкса:

= 18162.10 (|R| = 1.390е-11), = 10757.91 (|R| = 3.707е-07), = 17452.58 (|R| = 3.690е-11), p = 0.000; следовательно, подтверждается гипотеза о значимости всей корреляционной матрицы (переменные зависимы). Данный вывод для матрицы А вытекал уже из результатов использования t -критерия (высокая значимость коэффициентов корреляции по данному критерию), поэтому ряд авторов рекомендуют использовать критерий Бартлетта-Уилкса лишь в случае слабой корреляционной зависимости между переменными (Иберла, 1980). Если мы разделим все значения парных корреляций матрицы А на 100 (все r < 0.01), то значения χ² = 3.32 (|R| = 0.995), р = 1.0 и гипотеза о зависимости переменных отвергается. Дополнительно добавим в матрицу один значимый коэффициент корреляции: r_ij = r_ji = 0.465: в данном случае χ² = 180.33 (|R| = 0.780), и гипотеза о зависимости переменных принимается на уровне значимости р = 0.007. Также отметим зависимость критерия Бартлетта-Уилкса от объема выборки. Разделим значения парных корреляций матрицы А на 10 (все r < 0.1). В этом случае χ² = 237.60 (|R| = 0.721), р = 0.000 (n = 734), – принимается гипотеза о зависимости переменных. Если объем выборки был бы равен, например, 450, то тогда χ² = 144.72, р = 0.288, – отвергается гипотеза о зависимости переменных.

Критерий адекватности выборки Кайзера не зависит от объема выборки, но для него отсутствуют статистические таблицы значимости (Rencher, 2002; Ким и др., 1989):

, где – сумма квадратов элементов матрицы коэффициентов корреляции (исключая главную диагональ), å^q ij – сумма квадратов соответствующих частных коэффициентов корреляции. Критерий адекватности выборки сравнивает значения наблюдаемых коэффициентов корреляции со значениями частных коэффициентов корреляции. Частные корреляции оценивают взаимозависимости между переменными i и j при фиксированных значениях всех остальных переменных. Если корреляция между двумя переменными уменьшается, когда мы фиксируем значения других переменных, то это означает, что их взаимозависимость возникает частично через воздействие этих переменных; если же частная корреляция равна 0 или очень мала, то можно сделать вывод, что их взаимозависимость целиком обусловлена этим воздействием. В том случае, когда частная корреляция больше первоначальной корреляции между двумя переменными, можно заключить, что другие переменные ослабляли связь («маскировали» корреляцию) (Кендалл, Стьюарт, 1973). Небольшие значения критерия MSA указывают на то, что корреляции между парами переменных нельзя объяснить другими переменными и что использование факторного анализа нецелесообразно. Пороговые значения для критерия MSA по Кайзеру следующие (Ким и др., 1989): > 0.9 – безусловная адекватность; > 0.8 – высокая адекватность; > 0.7 – приемлемая адекватность; > 0.6 – удовлетворительная адекватность; > 0.5 – низкая адекватность; £ 0,5 – факторный анализ неприменим к выборке. Для наших данных были получены следующие значения критерия: MSA_A = 0.898, MSA_B = 0.786, MSA_C = 0.894. Таким образом, для матриц А и С по критерию MSA был достигнут высокий уровень адекватности применения факторного анализа, а для матрицы В – приемлемый.

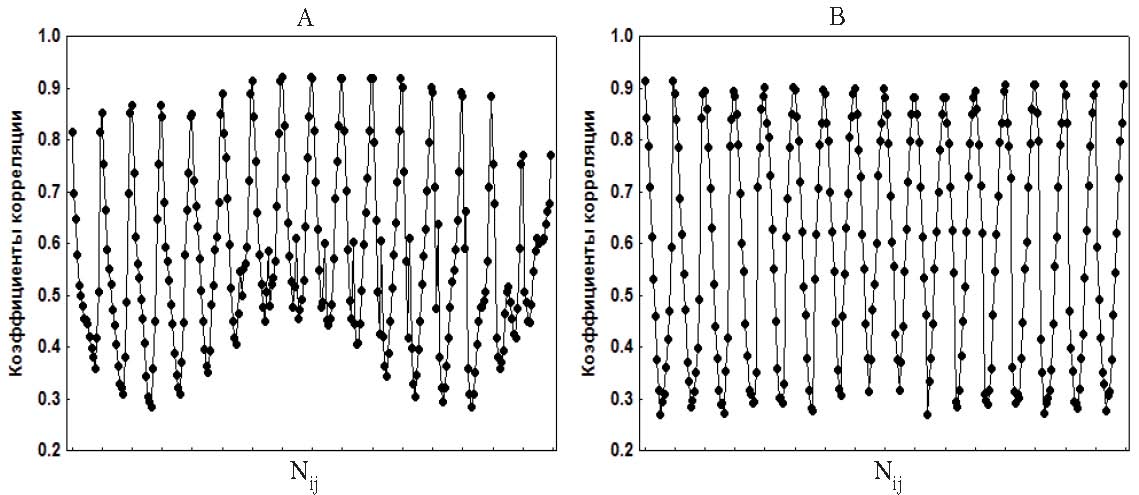
Рис. 1. Графики парных коэффициентов корреляции r_ij: (А) – матрица А, (В) – матрица М (последовательность векторов-строк)

Дополнительно мы решили рассмотреть графики парных коэффициентов корреляции, представив каждую матрицу в виде вектора, состоящего из последовательности строк (значения на главной диагонали исключались). На рис. 1, А (матрица А) хорошо просматривается периодичность в изменениях корреляции: максимумы образованы значениями парных коэффициентов корреляции показателей спектра сердечного ритма соседних частотных диапазонов (rи r), которые постепенно уменьшаются по мере увеличения расстояния между частотными диапазонами. Характерная высокая взаимозависимость между соседними частотными диапазонами становится еще более очевидной при анализе частных коэффициентов корреляции. На рис. 2, А (матрица А) отчетливо наблюдаются пики, образованные частными корреляциями показателей спектра соседних частотных диапазонов, при этом частные корреляции показателей спектра более удаленных частотных диапазонов колеблются около 0. (Заметим, что высокие значения 32 частных корреляций соседних частотных диапазонов, когда оставшиеся 104 близки 0, незначительно понижают показатель MSA.) Такая периодичность парных и частных корреляций наблюдается и для матриц В и С. Это позволило нам смоделировать с помощью программной среды «Delphi-5» матрицу корреляций, используя следующую формулу гармонических колебаний:

Х_i = Аm×Cos(2×π×f) + Аm×Sin(2×π×f) + Х_ср + RandG (M,SD), где Аm – амплитуда колебаний = 0.22, f – частота колебаний (с периодом = 22), Х_ср – среднее значение коэффициента корреляций = 0.599, RandG – функция для генерирования случайных чисел, распределенных по нормальному закону Гаусса с математическим ожиданием M и среднеквадратическим отклонением SD (M = 0, SD = 0.12).

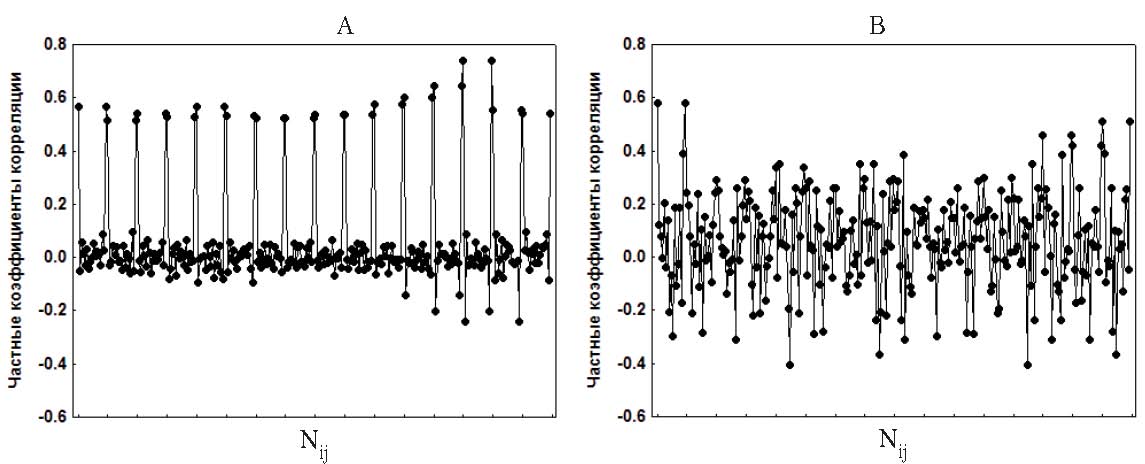
Рис. 2. Графики частных коэффициентов корреляции r_ij: (А) – матрица А, (В) – матрица М (последовательность векторов-строк)

Из полученной последовательности гармонических колебаний отбирались значения векторов-строк (m = 17, включая r_ij= 1.0) для модельной матрицы: максимальная амплитуда колебаний соответствовала значениям корреляций r показателей спектра соседних частотных диапазонов. Таким образом, были отобраны элементы для 100 матриц, средние значения по которым стали элементами модельной матрицы М. Коэффициент корреляции между элементами матриц А и М оказался равен 0.882, между соответствующими частными корреляциями r = 0.433. На рис. 1, В и 2, В представлены графики парных и частных коэффициентов корреляции матрицы М (последовательность векторов-строк). Для матрицы М критерий Бартлетта-Уилкса c² = 21867.75 (|R| = 8.466е-14), p = 0.000, а MSA = 0.914. В своем исследовании мы решили проверить, насколько близки будут факторные модели для матриц А и М, имеющих близкое распределение парных корреляций и значимые отличия в распределении частных корреляций переменных.

После подтверждения гипотезы о целесообразности применения факторной модели для анализа данных по четырем матрицам (критерии Бартлетта-Уилкса и MSA) на следующем шаге для выделения факторов (компонент) был использован метод главных компонент (Principal components). Модель компонентного анализа имеет следующий вид (Харман, 1972):

z = aF + aF+…+aF (j = 1, 2, …, m), где z – наблюдаемый признак (переменная), который линейно зависит от m некоррелированных между собой и упорядоченных по величине вклада в суммарную дисперсию признаков компонент F₁, F₂, …, F_m; m – число анализируемых признаков. При этом первая компонента дает максимально возможный вклад в суммарную дисперсию признаков, а последняя – минимальный. Главные компоненты независимы (парные корреляции равны 0), т. е. в геометрическом плане ортогональны. Модель компонентного анализа позволяет однозначно восстановить значения каждого из наблюдаемых признаков z_j по соответствующим значениям компонент F₁, F₂, …, F_m . Коэффициенты при компонентах a_ji называют нагрузками (loadings), они представляют собой линейную корреляцию между переменными и компонентами и выражают меру влияния компонента на признак.

Обычно суммарная дисперсия признаков раскладывается по главным компонентам таким образом, что первые несколько компонент k уже объясняют почти всю эту дисперсию, а остальные практически ничего не добавляют, поэтому совсем не обязательно выделять все m компонент. На практике ограничиваются несколькими первыми k, так как их оказывается достаточно для удовлетворительного сжатого описания всей исходной информации. С целью определения относительной значимости каждой главной компоненты F_i рассчитываются их собственные значения ( l_i ²); собственное значение (eigenvalue) – это часть суммарной по всем переменным дисперсии, которую объясняет компонента. Для вычисления собственного значения нужно суммировать квадраты нагрузок a по всем переменным данной компоненты F_i:

 , где m – число переменных.

В табл. 2 приведены собственные значения главных компонент, их доли в общей дисперсии и соответствующие кумуляты для корреляционных матриц А, В, С и М.

Таблица 2. Собственные значения главных компонент для корреляционных матриц А, В, С и М (N – номер компоненты)

Существует несколько правил отбора необходимого числа первых k главных компонент, которые формулируются в терминах собственных чисел (Rencher, 2002; Ким и др., 1989):

1. Оставить число главных компонент, которые объясняют заданный процент общей дисперсии. Его можно определить, исключив компоненты, которые учитывают менее 5% суммарной дисперсии переменных. Согласно табл. 2, данное условие выполняется при k = 4 для матриц А и С (соответственно, их суммарная доля дисперсии 87.5% и 86.9%), k = 5 для матрицы В (80.5%) и k = 3 для матрицы М (91.9%). Это правило основывается на исключении компонент с малым вкладом в суммарную дисперсию, поскольку они не имеют практической ценности (Харман, 1972).
2. Используя график собственных значений главных компонент (график «каменистой осыпи» – «scree graph»), определить точку «излома»: переход от резкого уменьшения собственных значений к их постепенному (с небольшим углом наклона линии графика) убыванию с ростом номера компоненты (метод предложен Кэттеллом). Для отбора используют главные компоненты с собственными значениями до данной точки «излома» (Rencher, 2002). Согласно рис. 3, В (матрица М), данное условие выполняется для первых трех главных компонент (k = 3). На графике, представленном на рис. 3, А (матрица А), единственная точка «излома» отсутствует; вместо этого собственные значения плавно изменяются (данная картина наблюдается и для матрицы С, для матрицы В – в интервале 4÷6 компонент). Такая неоднозначность (включая несколько точек «излома») характерна для многих графиков собственных значений и предлагает исследователю руководствоваться субъективными критериями в содержательных трактовках и описаниях (Ким и др., 1989).

3. Оставить число главных компонент, собственные значения которых превышают 1 (среднее собственное значение для матрицы корреляций). Данная эвристическая процедура была выработана Кайзером после длительных экспериментальных исследований (Ким и др., 1989). Согласно этой процедуре, k = 3 для матриц А, С и М и k = 4 для матрицы В (табл. 2).

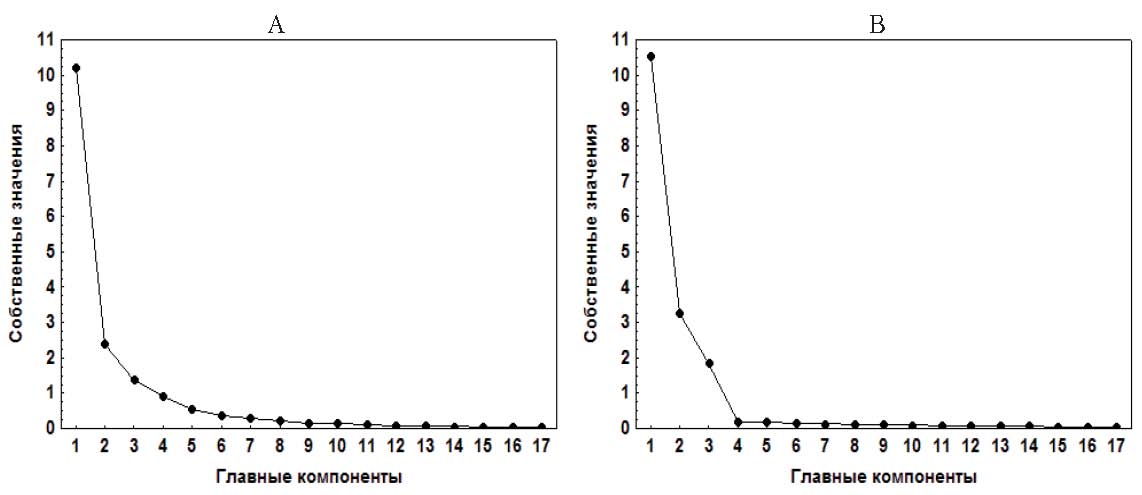
Рис. 3. Графики собственных значений главных компонент: (А) – матрица А, (В) – матрица М

Суммировав полученные результаты отбора первых главных компонент правилами, основанными на собственных числах, получим следующие результаты: для матрицы М по всем трем процедурам k = 3, для матриц А и С k = 3÷4 компонентам, для матрицы В – 4÷5 компонентам.

Отобранные на основе собственных значений главные компоненты позволяют нам перейти к построению факторной модели. Если метод главных компонент дает возможность проанализировать максимальные вклады в суммарную дисперсию признаков (используя собственные значения), то цель факторного анализа – поиск наилучшей аппроксимации корреляционных связей между признаками, для достижения которой используют вращение факторного пространства. Основную модель факторного анализа можно записать следующим способом (Харман, 1972):

z = aF + aF+…+aF +u (j = 1, 2, …, m), где z – наблюдаемый признак (переменная), который линейно зависит от k не коррелированных между собой (независимых, ортогональных) общих факторов F, F, …, F и характерной компоненты u; m – число анализируемых признаков. Коэффициенты при общих факторах aназываются факторными нагрузками (factor loadings) и представляют собой линейную корреляцию между переменными и общими факторами, отражая меру влияния общего фактора на признак. В общие факторы объединяются переменные, сильно коррелирующие между собой. Если в модели главных компонент вся дисперсия приписывается m компонентам (характерный компонент u_j всех признаков принимается равным 0, а число главных компонент равно числу исходных признаков), то в факторном анализе дисперсия каждой исходной переменной делится на две части: дисперсию, обусловленную наличием k общих для всех признаков факторов F₁, F₂, …, F_k (общность – communality), и дисперсию, обусловленную характерным, «специфическим» для признака z_j остаточным случайным компонентом u_j (специфичность или характерность), который включает в себя, как правило, ошибки измерения признака (Айвазян и др., 1989; Rencher, 2002). После построения всех главных компонент остаточная дисперсия оказывается равной 0, т.е. задача имеет точное математическое решение. В отличие от метода главных компонент, в случае факторного анализа возможность однозначного восстановления значений каждого из наблюдаемых признаков z по соответствующим значениям общих факторов F₁, F₂, …, F_k отсутствует. Исследователь стремится построить такую факторную модель, которая, с одной стороны, позволяет содержательно интерпретировать минимальное число латентных общих факторов, а с другой, как можно более полно объяснить с их помощью наблюдаемые взаимосвязи между исходными переменными, минимизируя зависимость отдельных признаков от их специфических остаточных случайных компонент. В рамках факторной модели искомые общие факторы могут рассматриваться в качестве причин (детерминантов), а исходные признаки – в качестве их следствий.

Возведенная в квадрат факторная нагрузка a_ji (коэффициент корреляции между фактором и переменной) характеризует степень общности (или перекрытия, совпадения) дисперсий данной переменной и данного общего фактора. Если полученные общие факторы не зависят друг от друга («ортогональное» решение), то общность переменной z_j по всем факторам (часть дисперсии переменной, совпадающей с дисперсиями всех факторов – h ² _j ) можно оценить через сумму квадратов факторных нагрузок переменной по факторам, включенным в модель (Иберла, 1980):

h ² _j =_åa ² _ji (j = 1, 2, …, m ), где a_ji – факторные нагрузки, m – число переменных, k – число общих факторов.

Значения общности переменной лежат в диапазоне от 0 до 1, они позволяют понять, какая часть дисперсии переменной объясняется общими факторами. Чем выше значение общности переменной, тем точнее факторная модель объясняет дисперсию анализируемого признака. Если взаимосвязь переменной с другими исследуемыми признаками крайне невысокая, ее общность будет низкой. Это может быть обусловлено тем, что переменная измеряет качественно отличный от других переменных показатель, либо ошибкой измерения.

Факторные нагрузки позволяют также вычислить, какую часть суммарной дисперсии переменных объясняет каждый фактор F_i ( l_i² ). Для этого рассчитываются собственные значения факторов (Иберла, 1980):

m li ² =åa ² ji (i = 1, 2, …, k), где a – факторные нагрузки, m – число переменных, k – j =1 - число общих факторов; разделив собственные значения факторов на число m, мы получим долю суммарной дисперсии переменных, которую объясняет каждый общий фактор, и сможем оценить их относительную значимость.

Для максимально возможной концентрации дисперсии исходных признаков на координатных осях выделенных общих факторов («контрастирования» факторных нагрузок) и облегчения содержательной интерпретации факторов используют различные методы вращения факторного пространства. Наиболее часто используется вращение по методу Varimax, при котором по каждому фактору минимизируется количество переменных, имеющих высокие нагрузки, что максимально увеличивает дисперсию факторов (максимизируются различия столбцов матрицы нагрузок). Это обеспечивает разделение факторов за счет уменьшения числа исходных переменных, связанных с каждым фактором, и упрощает их содержательную интерпретацию. Метод Varimax предполагает, что общие факторы ортогональны (независимы). В табл. 3 приведены матрицы факторных нагрузок (факторное отображение – factor pattern) для модели с тремя общими факторами: метод выделения факторов – метод главных компонент, метод вращения факторного пространства – Varimax.

Таблица 3. Матрицы факторных нагрузок для модели с тремя общими факторами F1¸F3: N – номер переменной, l² – собственное значение фактора (в скобках указана доля l² в общей дисперсии переменных).

Примеч.: жирным шрифтом выделены факторные нагрузки > 0.5.

Существует ряд статистических критериев для проверки гипотезы о значимости полученного факторного решения по исходной корреляционной матрице R. Все они основываются на оценке воспроизведенной с помощью факторной модели корреляционной матрицы R⁺ и матрицы остатков коэффициентов корреляции R^-= R – R⁺. Во многих из них используются определители матриц R⁺ и R^-.

1. Критерий Лоули-Бартлетта – проверка гипотезы о достаточности выделенных k общих факторов для воспроизведения корреляционной матрицы R⁺ (Иберла, 1980): χ² = (n–1)×ln(|R⁺|/|R|), где |R⁺| – определитель матрицы воспроизведенных корреляций, |R| – определитель исходной матрицы корреляций, n – объем выборки. Табличные значения χ_т ² рассчитываются для df = 0.5 [(m – k)² – m – k], где m – число переменных, k – число общих факторов. Если χ² > χ_т² , необходимо увеличить число общих факторов.
2. Критерий Бартлетта-Уилкса – проверка гипотезы об окончании процесса выделения факторов по матрице остатков R (Иберла, 1980). Данный критерий был описан нами выше. Единственное отличие заключается в том, что вместо определителя исходной матрицы корреляций |R| в формуле используется определитель матрицы |R−|. Если χ² > χ_т², переменные зависимы, выполняется условие для увеличения числа общих факторов¹.

При расчетах определителя матрицы необходимо учитывать относительную погрешность при решении системы линейных уравнений, обусловленную машинной точностью, с которой совершаются все операции с вещественными числами (Иберла, 1980). Если корреляционная матрица плохо обусловлена, то значения определителя будут очень чувствительны к таким погрешностям. Оценкой погрешности вычислений может служить число обусловленности матрицы (Cond): чем выше величина Cond, тем выше относительная погрешность вычислений. Плохо обусловленными могут считаться матрицы, для которых Cond >> 1 (Амосов и др., 1994). Например, для исходных матриц корреляций были получены следующие значения числа обусловленности: Сond_А = 3.342е+02, Сond_В = 9.341е+01, Сond_С = 3.035е+02, Сond_М = 3.880е+02. Число обусловленности для соответствующих матриц воспроизведенных корреляций и остатков при различных факторных решениях (количествах общих факторов) колебалось уже в диапазоне 3.074е+04÷3.896е+06. Плохая обусловленность корреляционных матриц ставит под сомнение результаты использования перечисленных критериев. Не случайно во всех случаях применения критерия Лоули-Бартлетта и Бартлетта-Уилкса были получены чрезвычайно высокие значения χ² (p = 0.000), не позволяющие сделать выбор между различными факторными решениями.

Чтобы обойти проблему, связанную с низкой обусловленностью матриц, были предложены критерии, не связанные с расчетом определителей.

1. Критерий Лоули и Максвелла (аппроксимация критерия Лоули-Бартлетта) (Иберла, 1980):

, где – коэффициенты корреляций матрицы остатков ^r (ост) j <i u_i ×u_j 22 (наддиагональные элементы), u_i и u_j – значения характеристических (специфических) компонент переменных z_i и z_j (равны соответствующим диагональным элементам матрицы остатков), n ¢ = n – (2m + 5)/6 – 2k/3, df = 0.5 [(m – k)² – m – k] (n – объем выборки, m – число переменных, k – число общих факторов). Для данного критерия нами также были получены очень высокие значения χ² (p = 0.000), не позволяющие сделать выбор между различными факторными решениями. В работе (Иберла, 1980) делается предупреждение, что применение данного критерия не всегда приводит к хорошим результатам.

2. Критерий Лоули (аппроксимация критерия Бартлетта-Уилкса) (Иберла, 1980):

 , где – коэффициенты корреляций матрицы остатков (наддиагональные элементы), n – объем выборки, df = m(m–1)/2 (m – число переменных). = n ×_år rij

Условие независимости остатков корреляции (χ² < χ_т² – нецелесообразно дальнейшее увеличение числа общих факторов) для рассматриваемых матриц было достигнуто при следующих значениях числа общих факторов. Матрицы А и С: k = 4, c_À ² =115.01, p = 0.904; с =121.41, p = 0.810 (k = 3, cÀ =309.21, p = 0.000; c ² _с =320.98, p = 0.000). Матрица В: k = 7, c ²=117.17, p = 0.941 (k = 6, c ² =176.97, p = 0.000). Матрица М: k = 3, c ² =19.26, p = 1.0 (k = 2, _c 2 =1026.67, p = 0.000). При использовании данного критерия необходимо учитывать зависимость от объема выборки. Например, если бы объем выборки для матрицы А был равен 350, то для k = 3 критерий Лоули c _À ² = 147.44, p = 0.237.

¹В «Statistica 6.0» значения общности переменных 2 приведены в соответствующих элементах главной диагонали матрицы R⁺, а специфичности u_j – матрицы R-.

3. Критерий Барта (Иберла, 1980): c ² = (n - 3) ×_å(z_ij - z )² , где z_ij – преобразование Фишера = 0.5×[(1 + r_ij)/(1– r_ij)] (r_ij – наддиагональные элементы коэффициентов корреляции матрицы остатков), z – среднее значение преобразований Фишера, n – объем выборки, df = 0.5×[(m – k)² – m – k] (m – число переменных, k – число общих факторов).

Оценки остатков по критерию Барта приводят к повышению значений числа общих факторов для матриц А и С: k = 5, c _À ² =57.94, p = 0.587; c ² _с =64.20, p = 0.365 (k = 4, c _À ² =108.83, p = 0.005; c ² _с =114.57, p = 0.002). Для матрицы М выводы совпали: k = 3, c_м ² =16.64, p = 1.0 (k = 2, c_м ² =1031.74, p = 0.000). Показательно, что для матрицы В даже при k = 10 нулевая гипотеза отвергалась (χ² > χ_т², p = 0.000): остатки корреляций статистически значимы, целесообразно продолжить увеличение числа общих факторов. Критерий Барта также зависит от объема выборки. Так, если бы объем матрицы А был равен 250, то для критерия Барта (k = 3) c _À ² = 100.38, p = 0.173.

Данные статистических критериев Лоули и Барта в целом подтвердили выводы, сделанные с помощью правил собственных значений главных компонент. Для матрицы М наиболее оптимальным является решение с тремя общими факторами (k=3). Для матриц А и С, согласно критерию Лоули, целесообразно рассмотреть содержательную интерпретацию моделей с тремя и четырьмя общими факторами. Критерий Барта дает завышенные оценки числа общих факторов (k=5) для матриц А и С. Для матрицы В использование статистических критериев приводит к чрезмерной переоценке числа общих факторов в модели, особенно в случае критерия Барта.

Для определения окончательного числа общих факторов обратимся к научным представлениям о природе спектральных показателей сердечного ритма. Международный стандарт по измерениям и физиологической интерпретации вариабельности сердечного ритма рекомендует рассматривать три частотные области в сердечном спектре, имеющие свои уникальные механизмы регуляции: VLF (0.00÷0.04 Гц), LF (0.04÷0.15 Гц) и HF (0.15÷0.40 Гц) (Heart Rate Variability, 1996). С учетом данных рекомендаций и полученных ранее выводов мы можем остановиться на факторной модели с тремя общими факторами.

Чтобы еще раз проверить правильность факторного решения, воспользуемся принципом «простой структуры», предложенным Тэрстоуном. Достижение простой факторной структуры с помощью вращения факторного пространства облегчает интерпретацию переменных и факторов, правда, концепция «простой структуры» неоднозначна и единых формальных критериев ее определения не существует (Ким и др., 1989). Но с точки зрения простой структуры мы должны стремиться к построению такой матрицы факторных нагрузок, в которой каждая переменная z_j имела бы высокую корреляцию (a_ji) только с одним фактором F_i. В табл. 3 мы выделили жирным шрифтом высокие значения факторных нагрузок a_ji > 0.5. Для всех матриц хорошо видны три группировки переменных, образованные соседними частотными диапазонами, которые имеют высокие нагрузки с отдельными факторами. Например, для матрицы А это V÷V (высокая корреляция с фактором 1), V÷V (высокая корреляция с фактором 2) и V₁₂÷V₁₇ (высокая корреляция с фактором 3). Как можно заметить, ряд переменных из этих групп имеют высокие нагрузки более чем с одним фактором: V – факторы 1 и 2, V и V – факторы 1 и 3. Такие переменные считаются сложными (они отражают влияние более чем одного фактора). Цель вращения состоит в минимизации числа таких переменных, затрудняющих интерпретацию факторов.

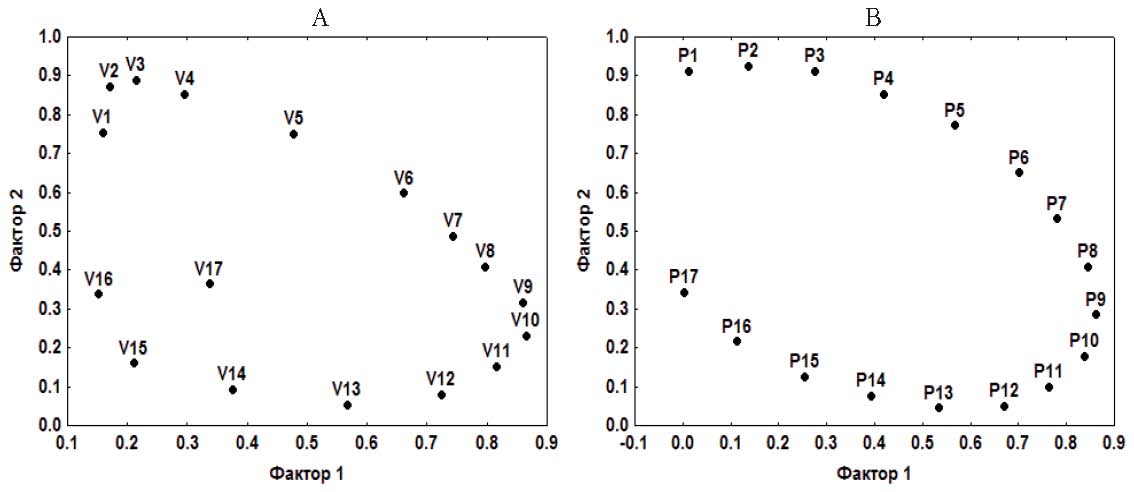
Рис. 4. Графики факторных нагрузок для переменных V₁÷V₁₇ матрицы А (А) и переменных P₁÷P₁₇ матрицы М (В)

Чтобы понять природу появления этих сложных переменных, обратимся к графической оценке простоты факторной структуры. Для этого построим график факторных нагрузок. На рис. 4 для матриц А и М изображено двухмерное факторное пространство, образованное ортогональными факторными осями 1 и 2. При наличии простой структуры факторные нагрузки группируются таким образом, чтобы иметь максимальные значения по одной факторной оси и минимальные по другой. В нашем случае факторные нагрузки принимают форму, близкую к эллипсу (отметим, что данная особенность характерна и для факторного решения с четырьмя общими факторами). Нарушение принципа простой структуры отражает характер внутренней взаимосвязи между переменными: высокая корреляция соседних частотных диапазонов и постепенное «затухание» корреляций с увеличением расстояния между диапазонами. Вращение факторного пространства привело к выделению взаимосвязанных между собой групп переменных (по принципу близости частотных диапазонов), но не смогло исключить наличие сложных переменных, «пограничных» для этих групп. При этом объем групп в различных факторах приблизительно равен, как и собственные значения факторов (λ²). Частотные диапазоны, которые «детерминируют» факторы, совершенно не совпадают с результатами многочисленных физиологических исследований, на которые опираются международные рекомендации (Heart Rate Variability, 1996). Например, для матрицы А (табл. 3): первый фактор имеет высокую корреляцию (a_ji > 0.6) с переменными частотного диапазона 0.10÷0.24 Гц, второй фактор – с переменными частотного диапазона 0.0÷0.10 Гц, третий фактор – с переменными частотного диапазона 0.24÷0.50 Гц. В этом случае правильно говорить о том, что существует корреляция между факторами и переменными, но ошибочно было бы утверждать, что выделенные латентные факторы детерминируют исследуемые переменные. Заметим, что факторная нагрузка для переменной V₁₇ (0.40÷0.50 Гц) несколько выпадает из «ансамбля» (рис. 4, А). Напомним, что международные рекомендации ограничивают высокочастотный диапазон спектра сердечного значением 0.40 Гц (Heart Rate Variability, 1996).

В завершение нашего анализа произведем сравнение факторных структур для четырех матриц. Для этого воспользуемся коэффициентом конгруэнтности (Харман, 1972):

, где a – элементы матрицы нагрузок фактора p, a – элементы матрицы нагрузок фактора q, i – номер переменной, m – число переменных. Показатель j _pq изменяется в диапазоне от +1 (полное совпадение) или –1 (полное обратное совпадение) до 0 (полное отсутствие связи). Для данного показателя отсутствуют статистические таблицы значимости. Экспериментально было предложено: j _pq = 0.999984÷0.93981 – факторы конгруэнтны, j _pq = 0.459717 – недостаточно для определения конгруэнтности. Для усиления различий (совпадений) между факторами предложен следующий индекс контрастности:

, где ln – натуральный логарифм. Согласно полученным результатам (табл. 4), между факторными решениями исследуемых матриц существует высокая конгруэнтность; особенно высоко совпадение факторных нагрузок матриц А и С.

Таблица 4. Коэффициенты конгруэнтности для факторов F1÷F3 исследуемых матриц (в скобках приведены значения индекса контрастности Z)

Примеч.: жирным шрифтом выделены коэффициенты конгруэнтности > 0.90.

По аналогии с матрицей А мы построили две дополнительные матрицы А₁ и А₂, разделив исходный объем данных (n=734) на две равные половины (n₁=367, n₂=367). И матрица А₁, и матрица А₂ имели высокие коэффициенты конгруэнтности с факторным решением матрицы А. Также дополнительно мы провели факторный анализ коэффициентов корреляции Спирмена для исходных переменных D₁÷D₂₃ и пришли к схожему факторному решению с тремя общими факторами: суммарная доля дисперсии 91.46%, l₃² >1, h₁² =31.6% (D÷D, 0.28÷0.46 Гц), ² =31.4% (D÷D, 0.0÷0.14 Гц), ² =28.5% (D÷D, 0.14÷0.28 Гц).

Заключение

1. Частотный диапазон спектра сердечного ритма был разбит на 25 равных областей, которые после проверки нормальности распределения показателей мощности спектра были сгруппированы в 17 переменных (см. табл. 1). Факторный анализ был выполнен для четырех корреляционных матриц: А – нормальное распределение переменных (предварительное преобразование к нормальному виду), параметрическая корреляция Пирсона; В – нарушение нормального распределения переменных (без преобразования к нормальному виду), параметрическая корреляция Пирсона; С – нарушение нормального распределения переменных (без преобразования к нормальному виду), непараметрическая корреляция Спирмена; М – моделирование периодичности в изменениях парных коэффициентов корреляции: максимум амплитуды – корреляция соседних частотных диапазонов, уменьшение корреляции по мере увеличения расстояния между частотными диапазонами (рис. 1). Для матриц А и М было достигнуто сходство в распределении парных корреляций, при этом распределения частных корреляций различались (рис. 2).
2. Для всех четырех матриц критериями Бартлетта-Уилкса и Кайзера была подтверждена целесообразность использования факторной модели. Для матриц А и С по критерию MSA был достигнут уровень высокой адекватности, для матрицы М – уровень безусловной адекватности, для матрицы В – уровень приемлемой адекватности факторному анализу.
3. Используя правила собственных чисел для отбора общих факторов (k), выделенных методом главных компонент (табл. 2), были получены следующие факторные решения: для матриц А и С k = 3÷4, для матрицы В k = 4÷5, для матрицы М k = 3.
4. Значимость факторных решений (после вращения факторного пространства методом Varimax) была проанализирована с помощью ряда статистических критериев, из которых наиболее ценными оказались критерии Лоули и Барта. Результаты критерия Лоули в целом подтвердили выводы, сделанные с помощью правил собственных значений главных компонент: для матрицы М наиболее оптимальным является решение с тремя общими факторами (k=3); для матриц А и С целесообразно рассмотреть содержательную интерпретацию моделей с тремя и четырьмя общими факторами. Критерий Барта дает идентичные оценки числа общих факторов (k=3) для матрицы М и завышает для матриц А и С (k=5). Для матрицы В использование данных статистических критериев приводит к чрезмерной переоценке числа общих факторов в модели (особенно в случае критерия Барта).
5. С учетом научных представлений о природе спектральных показателей сердечного ритма была выбрана факторная модель с тремя общими факторами. Для заключительной проверки правильности факторного решения был использован принцип «простой структуры». Анализ двухмерного факторного пространства позволил установить нарушение принципа простой структуры, вызванное характером внутренних взаимосвязей между переменными: высокая корреляция соседних частотных диапазонов и постепенное «затухание» корреляций с увеличением расстояния между диапазонами. Вращение факторного пространства привело к выделению взаимосвязанных между собой групп переменных (по принципу близости частотных диапазонов) и появлению сложных переменных, «пограничных» для этих групп (табл. 3). Объем групп в различных факторах был приблизительно равен, как и собственные значения факторов. Частотные диапазоны, с которыми факторы имеют высокую корреляцию, совершенно не совпадают с результатами многочисленных физиологических исследований. В этом случае было бы ошибочно утверждать, что выделенные латентные факторы детерминируют (регулируют) исследуемые переменные, и на этом основании строить психофизиологическую классификацию объектов исследования, как это представлено, например, в работах Н. Н. Даниловой.
6. Для сравнения факторных структур четырех матриц был использован коэффициент конгруэнтности. Согласно полученным результатам (табл. 4), между факторными решениями исследуемых матриц существует высокая конгруэнтность. Особенно высоко совпадение факторных нагрузок матриц А и С.
7. Использование в факторном анализе переменных с выраженными нарушениями нормальности распределения (матрица корреляций Пирсона В) привело к завышению числа отобранных общих факторов, чему также способствовали статистические процедуры, основанные на собственных значениях главных компонент и чрезмерной переоценке числа общих факторов на основании применения критерия Лоули и особенно критерия Барта (подтверждается чувствительность статистических критериев к допущению о многомерном нормальном распределении исходных переменных; см. Справочник по прикладной статистике, 1990). В то же время факторный анализ для матрицы корреляций Спирмена этих переменных (С) продемонстрировал практически полное совпадение с результатами нормально распределенных переменных, представленных матрицей корреляций Пирсона (А). Также мы получили высокое согласие факторных решений между матрицей А и модельными данными матрицы М, имеющими близкое распределение парных корреляций и значимые отличия в распределении частных корреляций переменных.

Таким образом, при выраженных нарушениях нормальности распределения исследуемых показателей в качестве исходных данных для проведения факторного анализа можно рекомендовать:

а) матрицу парных коэффициентов корреляции Пирсона (параметрическая статистика) с предварительным преобразованием распределений показателей к нормальному виду;

б) матрицу парных коэффициентов корреляции Спирмена (непараметрическая статистика) без предварительного преобразования распределений показателей к нормальному виду.

В заключение необходимо заметить, что факторный анализ, подобно регрессионному, можно отнести к области математического моделирования: создание модели объекта исследования в форме математического уравнения взаимосвязей исследуемых показателей с факторами. Но любая модель отражает только некоторые характерные черты объекта и никогда не бывает его точной копией. Для одного и того же объекта можно создать множество моделей (Вучков и др., 1987). Поэтому для построения и проверки факторной модели исследователю необходимо использовать как можно более полный набор процедур, критериев и научных представлений об объекте исследования: рассмотреть допущение о многомерном нормальном распределении исходных переменных; выбрать тип матрицы парных коэффициентов корреляции в качестве исходных данных; проверить целесообразность применения факторной модели анализа к исходным данным; выполнить процедуры отбора общих факторов; оценить значимость полученного факторного решения с помощью статистических критериев и принципа «простой структуры».

К сожалению, объем журнальной публикации не позволяет нам проанализировать факторные решения с зависимыми (облическими) факторами, сравнить метод главных компонент с другими методами выделения факторов, а Varimax – с другими методами вращения факторного пространства. Наши исследования показали, что для исходных данных – значений спектра мощности сердечного ритма в заданных частотных диапазонах – метод главных компонент в сочетании с Varimax-вращением является наиболее оптимальным с точки зрения построения факторной модели. Именно на этом мы и постарались детально остановиться в нашей статье.

1. Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: Классификация и снижение размерности. М.: Финансы и статистика, 1989. 607 c.
2. Амосов А. Л., Дубинский Ю. Л., Копченова Н. В. Вычислительные методы для инженеров. М.: Высшая школа, 1994. 544 с.
3. Вучков И., Бояджиева Л., Солаков Е. Прикладной линейный регрессионный анализ. М.: Финансы и статистика, 1987. 239 с.
4. Данилова Н. Н. Сердечный ритм и информационная нагрузка // Вестник МГУ. Серия 14 (Психология). 1995. № 4. С. 14–19.
5. Данилова Н. Н. Стрессоустойчивость как индивидуальная особенность // Доклады I-й Международной конференции памяти А. Р. Лурия. М.: МГУ, 1998. С. 177–192.
6. Данилова Н. Н., Астафьев С. В. Изменения вариабельности сердечного ритма при информационной нагрузке // Журн. выс. нерв. деят. им. Павлова. 1999. Т. 49. № 1. С. 28–38.
7. Зырянов Б. А., Власов С. Н., Костромин Э. В. Методы и алгоритмы обработки случайных и детерминированных периодических процессов. Свердловск: УГУ. 1990. 116 с.
8. Иберла К. Факторный анализ. М.: Статистика, 1980. 398 с.
9. Кендалл М., Стьюарт А. Статистические выводы и связи. М.: Наука. Т. 2. 1973. 899 с.
10. Ким Дж.-О., Мьюллер Ч. У., Клекка У. Р., Олдендерфер М. С., Блэшфилд Р. К. Факторный, дискриминантный и кластерный анализ. М.: Финансы и статистика, 1989. 215 с.
11. Лоули Д. Н., Максвелл А. Э. Факторный анализ как статистический метод. М.: Мир, 1967. 145 с.
12. Машин В. А. Зависимость показателей вариабельности сердечного ритма от средней величины R-R интервалов // Рос. физиол. журн. им. И. М. Сеченова. 2002. Т. 88. № 7. С. 851–855.
13. Справочник по прикладной статистике / Под ред. Э. Ллойда, У. Ледермана, С. А. Айвазяна, Ю. Н. Тюрина. Т. 2. М.: Финансы и статистика, 1990. 526 с.
14. Хальд А. Математическая статистика с техническими приложениями. М.: Изд. иностранной литературы, 1956. 663 с.
15. Харман Г. Современный факторный анализ. М.: Статистика. 1972. 487 с.
16. Heart Rate Variability: Standards of Measurement, Physiological Interpretation, and Clinical Use. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology // Circulation. 1996. V. 93. № 5. P. 1043–1065.
17. Rencher A. C. Methods of multivariate analysis. Wiley. 2002. 739 p.