Анализ показателей нравственного состояния общества в европейских странах: оценка адекватности факторной модели с использованием критерия, сформированного на основе самоорганизующихся карт признаков Кохонена

Корректное использование метода максимального правдоподобия для идентификации значений свободных параметров и оценки степени адекватности факторной модели в случае конфирматорного факторного анализа результатов вейвлет-преобразований предполагает проверку многомерной нормальности распределения наблюдаемых переменных. Эта процедура является трудоемкой и зачастую невозможной из-за малой выборки исследуемых данных. Для преодоления этой проблемы предлагается новый статистический критерий оценки степени адекватности факторных моделей дисперсионных составляющих в рамках используемой в исследовании выборки. Данный критерий опирается на возможности самоорганизующихся карт признаков Кохонена и позволяет снять с результатов наблюдений ограничения, связанные с их вероятностным распределением. Преимущества предлагаемого критерия: – отсутствие необходимости проверки многомерной нормальности распределений наблюдаемых переменных; – доступность простой процедуры оценки статистических ошибок второго рода; – возможность оценки наиболее вероятного процента статистически значимых отклонений компонентов вектора невязки псевдорешения. В статье приводятся теоретические основы разработки предлагаемого критерия, а также результаты применения данного критерия в исследовании выделения общего фактора и оценке его влияния на изменчивость социально-экономических показателей европейских стран.

Введение

В статьях (Kuravsky и др., 2009) рассматривается альтернативный вариант конфирматорного факторного анализа (КФА), позволяющий строить и идентифицировать факторные модели дисперсионных составляющих по выборочным данным. Учитывая тематику и научную направленность журнала «Экспериментальная психология», автор по мере возможности будет вносить дополнительные пояснения, касающиеся некоторых деталей проведенного ранее анализа. В исследовании (Куравский и др., 2010), проведенном автором совместно с научным руководителем и сотрудниками Института психологии РАН, возможности альтернативного КФА использовались для проверки гипотезы о существовании влияния общего фактора на изменчивость ряда социально-экономических показателей в европейских странах, составляющих индекс нравственного состояния общества (Юревич, Ушаков, 2007; Юревич, 2009), а также для выявления ряда частных закономерностей развития исследуемых показателей. В данном исследовании проверяется гипотеза о влиянии общего латентного фактора на изменчивость показателей нравственного состояния общества. В качестве анализируемых данных была использована выборка значений индекса коррупции (K), индекса неравенства доходов Джини (D) и индекса убийств (U) для 22 стран, входящих в состав Евросоюза и декларирующих информацию по указанным индексам, подсчитываемым ежегодно в открытых источниках. Для исследования были взяты значения индексов за 1998, 1999, 2000 и 2001 годы. Таким образом, выборка значений анализируемых индексов, обозначаемых как K₁₉₉₈, K₁₉₉₉, K₂₀₀₀, K₂₀₀₁, D₁₉₉₈, D₁₉₉₉, D₂₀₀₀, D₂₀₀₁, U₁₉₉₈, U₁₉₉₉, U₂₀₀₀, U₂₀₀₁, может быть представлена в виде таблицы с 12 столбцами (параметрами) и 22 строками (объектами). Альтернативный КФА, при помощи которого проводилось указанное исследование, использует метод максимального правдоподобия (ММП) для идентификации значений свободных параметров модели и оценки степени ее адекватности (степени согласования выборочных дисперсий и ковариаций исследуемых показателей с аналогичными оценками максимального правдоподобия, полученными путем идентификации свободных параметров факторной модели). Малая выборка значений переменных не позволила авторам достоверно оценить вид распределения исходных данных, а следовательно, и рассматривать полученный набор оценок свободных параметров модели как оптимальный. Данная статья посвящена описанию нового критерия оценки степени адекватности факторных моделей дисперсионных составляющих и порядка его применения, а также пояснениям по вейвлет-преобразованиям исходных данных и способу перехода от наглядного представления факторной модели в виде путевой диаграммы к системе линейных уравнений.

Гипотеза исследования и преобразование данных

Сотрудниками Института психологии РАН была выдвинута гипотеза о наличии единого общего фактора, который характеризуется исследователями как нравственность в ее широком понимании (Юревич, Ушаков, 2007; Юревич, 2009), влияющего на социальноэкономические показатели (индекс коррупции K, индекс неравенства доходов Джини D и индекс убийств U).

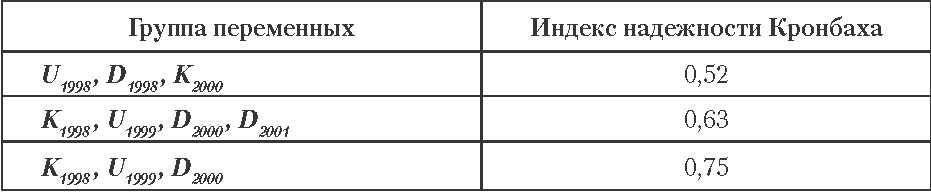
Указанная гипотеза в первом приближении частично подтверждается оценками альфа Кронбаха (Клайн, 1994), приведенными в табл. 1.

Таблица 1. Группы переменных с высоким значением индекса надежности Кронбаха.

Представление исследуемых временных рядов в альтернативном варианте КФА формируется с помощью дискретного вейвлет-преобразования (Добеши, 2001) с использованием ортогональных вейвлетов Добеши 4-го порядка, позволяющего выявлять различия в характеристиках анализируемых социально-экономических процессов (которые представлены в виде временных рядов значений индексов K, D и U) при различных шкалах измерений на всем протяжении интервала наблюдений.

Дискретное вейвлет-преобразование имеет смысл проводить в случае, когда существует необходимость сократить размерность анализируемых временных рядов (соответственно, снизить размерность и сложность задачи моделирования) без значимых потерь полезной эмпирической информации. Помимо этого вейвлет-преобразования могут быть использованы для устранения возможных влияний шумовых составляющих, а также для выделения интересующей исследователя периодичности в исследуемых процессах и представления ее в гораздо более компактной форме при помощи набора вейвлет-коэффициентов, каждый из которых соответствует определенному периоду наблюдений (т. е. положению на временной оси) и определенному масштабу детализации (т. е. диапазону на оси частот). Таким образом, вейвлет-коэффициенты, являясь мерой относительного вклада базисной составляющей в динамику процесса в различных частотных диапазонах (на различных масштабах), отражают распределение амплитуды процесса на заданном диапазоне частот и на всем интервале наблюдений. Их нужно понимать в данной работе как один из способов представления (кодирования) значений анализируемых параметров, который содержит в себе все закономерности и характеристики исследуемого временного ряда. В рамках этой работы вейвлет-преобразование было использовано с целью демонстрации возможности его применения в случае коротких временных рядов (от четырех временных точек). Тем не менее, автор открыт для дискуссии о необходимости и обоснованности применения вейвлетпреобразований в случае коротких временных рядов и возможности содержательной интерпретации результатов таких преобразований. Данные вопросы требуют детального разбора, и их рассмотрение должно представлять собой отдельное самостоятельное исследование.

Вычисление вейвлет-коэффициентов выполняется в среде графического программирования LabVIEW 8.2 с использованием дискретного вейвлет-преобразования Добеши 4-го порядка. Такое преобразование использует специальные масштабирующую a(s) и детализирующую c(s) функции, которые определяются, соответственно, своими коэффициентами h_n и g_n :

Вейвлет-преобразование анализируемого временного ряда s(t) производится в соответствии с итерационным пирамидальным алгоритмом Малла:

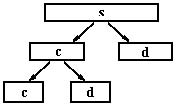
Рис. 1. Схема алгоритма Малла

Как показано на рис. 1, данный алгоритм позволяет подсчитывать вейвлет-коэффициенты D_m,k, характеризующие изменение значений анализируемого временного ряда на заданном уровне детализации m для определенного временного сдвига k.

Подробнее о теории вейвлетов можно прочитать в соответствующей технической литературе (Добеши, 2001).

Вейвлет-преобразования могут использоваться в различных прикладных областях науки для решения таких задач, как очистка сигналов произвольной природы от шума, сжатие сигналов и изображений, выявление и выделение тренда, применяться для спектрального анализа, а также кратномасштабного анализа, когда вейвлет-преобразования позволяют рассматривать исследуемые временные ряды с интересующей исследователя степенью детализации (в нужном масштабе). Теория вейвлетов применима не только к решению подобных задач технического характера, но может быть полезна в социологических и психологических задачах (Шустенкова, 2008).

Исходные временные ряды, состоящие из четырех значений каждый, позволяют получить четыре вейвлет-коэффициента. Первые два характеризуют вклад несущей составляющей (тренд) на всем интервале наблюдений (четыре года), а другие два характеризуют выраженность изменения значений исследуемых индексов в периоды наблюдений с 1998 по 1999 год и с 2000 по 2001 год. Именно эти коэффициенты и были выбраны в качестве наблюдаемых переменных, что позволило сократить размерность задачи в два раза.

Вейвлет-коэффициенты, соответствующие периоду с 1998 по 1999 год, обозначены как KW₃, DW₃ и UW₃, а коэффициенты, соответствующие периоду с 2000 по 2001 год, как KW₄, DW₄ и UW₄. (см. рис. 2).

Конфирматорная факторная модель

На рис. 2 в виде путевой диаграммы представлена факторная модель дисперсионных составляющих, которая использовалась для выявления степени факторного взаимодействия и проверки гипотезы о наличии общего фактора, влияющего на наблюдаемые переменные.

Путевая диаграмма (Loehlin, 1987) – это наглядный способ представления прикладной факторной модели, которая конструируется исходя из научной гипотезы исследования. Путевая диаграмма изображается графически на этапе проектирования модели и используется как отправная точка для перехода к системе уравнений, описывающей модель в формализованном виде (для этого могут быть использованы специальные правила обхода путей). Свободные параметры формализованной факторной модели затем могут быть идентифицированы при помощи подходящего метода решения систем линейных уравнений (модель дисперсионных составляющих является линейной).

В моделях дисперсионных составляющих свободными параметрами являются дисперсии и ковариации латентных гипотетических факторов. Конфирматорная модель дисперсионных составляющих подразумевает наличие системы уравнений, выражающих дисперсии и ковариации наблюдаемых переменных через линейные комбинации неопределенных свободных параметров модели. Для того чтобы идентифицировать модель, используется метод наименьших квадратов (МНК), который позволяет найти оптимальное сочетание дисперсий и ковариаций латентных факторов. Поскольку в общем случае МНК не предполагает нахождения точного решения системы, при помощи этого метода находится псевдорешение x_*, которое при подстановке вместо вектора неизвестных x обеспечивает наилучшее согласование левой и правой части системы Ax = b, где A – матрица коэффициентов при свободных параметрах, x – вектор-столбец неизвестных свободных параметров модели, b – свободный вектор наблюдаемых статистик (дисперсий и ковариаций исследуемых переменных). Следует указать, что в случае использования модели дисперсионных составляющих матрица A будет состоять из единиц и нулей, показывая, какие факторные дисперсии и ковариации описывают дисперсии и ковариации наблюдаемых переменных.

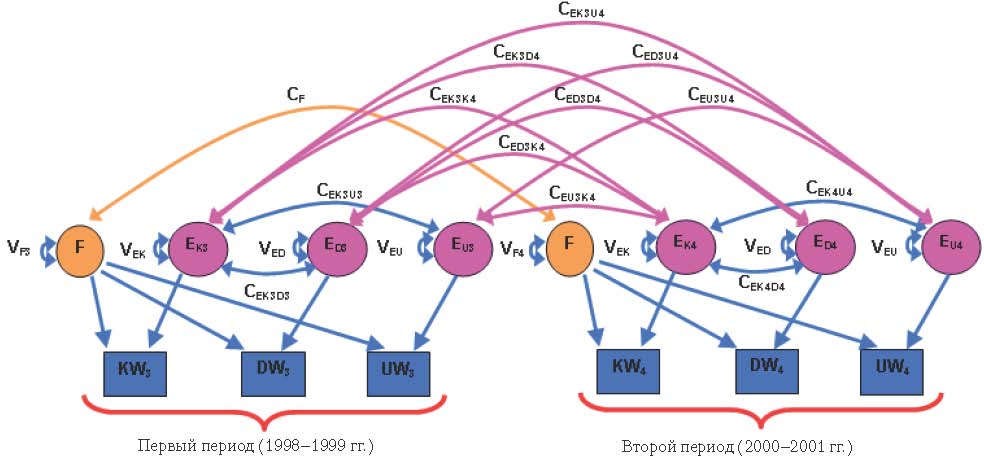
Рис. 2. Модель для проверки гипотезы о наличии общего фактора, влияющего на социально-экономические показатели в европейских странах: общий фактор обозначен как F; специфические факторы, влияющие на переменные K, D и U, – как Eи E; V – дисперсии общего фактора; V – дисперсии специфических факторов; C– ковариации между специфическими факторами; C– ковариация между фактором F в первом и втором периоде; факторные нагрузки равны единице и не указаны

При этом степень согласования модели и наблюдений (или, другими словами, статистическая значимость отличий между теоретическими и эмпирическими оценками дисперсий и ковариаций) может оцениваться по методу максимального правдоподобия, описанному в статьях, посвященных более детальному рассмотрению альтернативного варианта КФА (Куравский и др., 2009 a; Kuravsky, Baranov, 2008).

Теперь вернемся к конкретной модели, описывающей влияние единого общего фактора и специфических факторов на показатели KW₃, DW₃, UW₃ и KW₄, DW₄ и UW₄. Идентифицированные при помощи МНК дисперсии и корреляции латентных факторов представлены на рис. 3¹. Следует отметить высокие положительные корреляции между специфическими факторами E_D3 и E_D4, а также высокие отрицательные корреляции между специфическими факторами E_U3 и E_U4, E_K4 и E_U4.

 Рис. 3. Идентифицированные параметры факторной модели

Новый критерий для оценки адекватности факторной модели

Известно, что метод максимального правдоподобия, описанный ранее (Куравский и др., 2009 b; Kuravsky, Baranov, 2008) для альтернативного варианта КФА, подразумевает нормальное распределение значений наблюдаемых переменных. Однако используемые в проведенном нами исследовании выборки слишком малы (22 страны), что не позволило осуществить надежную проверку многомерной нормальности распределения исходных данных. Этот факт ставит под вопрос корректность интерпретации результатов, поскольку оценка степени адекватности предлагаемой модели проводится на выборке с неизвестным вероятностным распределением анализируемых параметров.

Для преодоления этой и подобных проблем, возникающих при использовании метода максимального правдоподобия, предлагается новый статистический критерий (Kuravsky et al., 2009; Мармалюк, 2010), использующий возможности самоорганизующихся карт признаков Кохонена (Галушкин, 2000; Куравский и др., 2003), которые относятся к типу нейронных сетей, обучаемых без учителя, и выполняют задачу кластеризации входных векторов наблюдений. Схема предлагаемого критерия представлена на рис. 4.

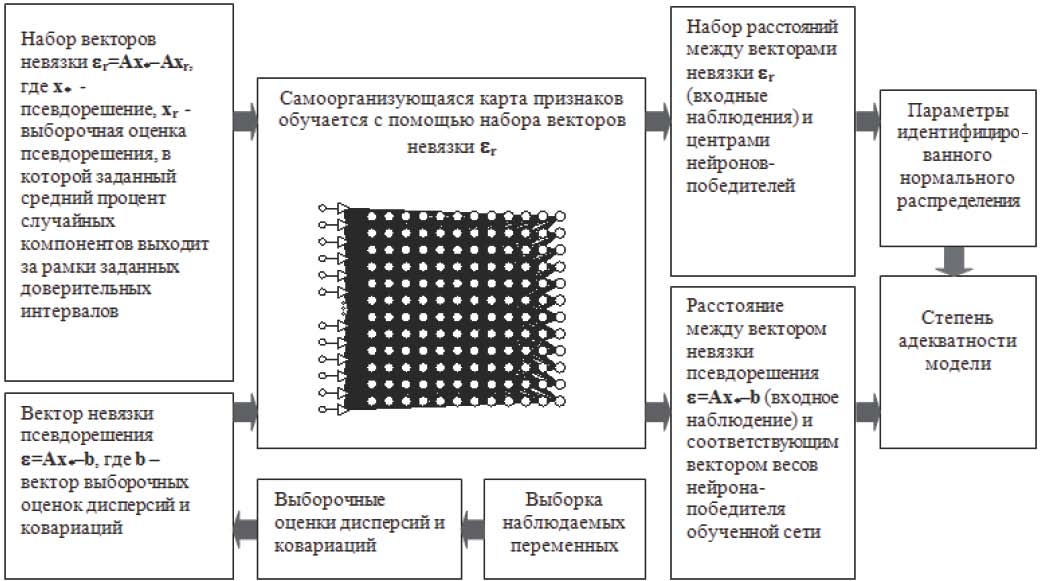
Рис. 4. Процедура оценки степени адекватности факторной модели с помощью самоорганизующихся карт признаков

Оценка степени адекватности основывается на сравнении вектора невязки псевдорешения ɛ=Ax–b с выборкой случайных векторов невязки ɛ =Ax–Ax , где x – это выборочная оценка псевдорешения, в которой определенный процент случайных компонентов выходит за рамки доверительных интервалов. Векторы невязки ɛ и ɛ подсчитываются по рассматриваемой факторной модели. Генерация выборки векторов невязки реализована в среде графического программирования National Instruments LabVIEW 8.2.1 Professional Edition.

Выборочные оценки дисперсий вычисляются при помощи следующей формулы, полученной из выражения для распределения выборочной дисперсии нормально распределенной случайной величины:

где V_S – оценка выборочной дисперсии, N – размер генерируемой выборки векторов невязки, V – дисперсия, входящая в состав найденного оптимального псевдорешения,

N-1 ^– случайный элемент, распределенный как χ² с N–1 степенями свободы. Формируемые оценки ковариаций подсчитываются через соответствующие значения выборочных корреляций, исходя из предположения, что их преобразование Фишера аппроксимируется нормальным распределением, а именно: распределение статистики

где r – выборочная корреляция, может быть аппроксимировано нормальным распределением со средним значением 1 1+r,

где ρ – значение корреляции, и дисперсией .

Значения преобразования Фишера вычисляются для каждой ковариации, входящей в псевдорешение, а корреляции ρ заменяются соответствующими результирующими корреляциями. Необходимые корреляции восстанавливаются при помощи обратного преобразования Фишера вышеупомянутых сгенерированных значений. После восстановления они конвертируются в ковариации, входящие в состав псевдорешения.

Сгенерированные дисперсии и ковариации составляют векторы псевдорешений x (в том же порядке, в каком расположены дисперсии и ковариации, формирующие вектор ^r оптимального псевдорешения x_*: этот порядок определяется составленной системой уравнений прикладной модели) и позволяют формировать образцы векторов невязки ɛ _r =Ax_* –Ax_r, необходимые для дальнейшего обучения самоорганизующейся карты признаков Кохонена подходящей размерности, а затем для получения наборов евклидовых расстояний между векторами невязки ɛ _r, используемых в качестве входных данных, и центрами (весовыми векторами) нейронов-победителей обученной сети.

Самоорганизующаяся карта признаков Кохонена – это соревновательная нейронная сеть с обучением без учителя, которая выполняет задачу кластеризации входных наблюдений и является методом проецирования многомерного пространства в пространство с более низкой размерностью (чаще всего двухмерное). Самоорганизующаяся карта состоит из компонент, называемых узлами или нейронами. Нейроны формально описываются векторами «весов», характеризующих положение центров нейронов в n-мерном пространстве (n – размерность входа сети, количество признаков в обучающих векторах). Исходное распределение центров нейронов случайно.

Алгоритм обучения сети последовательно подает на ее входы обучающие наблюдения (в данном случае это вектора невязки ɛ _r) и выбирает радиальный элемент с ближайшим центром (нейрон-победитель). Центр этого элемента и центры его «соседей» изменяются таким образом, чтобы минимизировать евклидово расстояние до входного наблюдения. Циклический процесс обучения, перебирающий входные данные, заканчивается по достижении картой допустимой (заранее заданной аналитиком) погрешности или по совершении заданного количества итераций.

По завершении обучения выходом сети считаются евклидовы расстояния от каждого сгенерированного вектора невязки ɛ до соответствующего нейрона-победителя r сети. После обучения на сеть подается также вектор невязки оптимального псевдорешения ɛ, для которого тоже рассчитывается расстояние до соответствующего выигравшего нейрона.

Принимая во внимание метрику евклидового расстояния и высокую размерность векторов невязки, типичную для практических задач, можно утверждать (по центральной предельной теореме), что полученные расстояния нормально распределены.

Сравнение выборочных распределений расстояний для различных процентных соотношений случайных компонентов, выходящих за рамки доверительных интервалов, позволяет выявить наиболее правдоподобную покомпонентную структуру статистически значимых отклонений от вектора невязки псевдорешения ɛ.

Таким образом, оценки средних значений и дисперсий полученных наборов расстояний идентифицируют полученные распределения и позволяют вычислить вероятность превышения расстояния между вектором невязки псевдорешения ɛ и соответствующим центром нейрона-победителя, что делает возможным оценить степень адекватности модели.

Оценка степени адекватности модели

Перед обучением сети Кохонена подходящей размерности была сгенерирована выборка из 64 псевдорешений x_i, в которых все компоненты лежат в своих доверительных интервалах. Затем вычислялись соответствующие вектора невязки ɛ= Ax–Ax (i = 1,…,64), i * i

которые использовались для обучения сети Кохонена на радиальных базисных функциях размерности 8х8 (см. рис. 5) в течение 100 эпох. Создание и обучение сети осуществлялось в пакете программ STATISTICA Neural Networks (Нейронные сети..., 2000). В начале обучения количество «соседей» было равно максимальному значению (8 соседей), а в конце обучения – минимальному (0 соседей).

Далее было сгенерировано 20 выборок, состоящих из 64 псевдорешений каждая, причем сгенерированные псевдорешения соответствовали 5 %, 10 % … 100 % случайных компонентов, выходящих за рамки своих доверительных интервалов. Данная выборка использовалась для верификации сети, или, другими словами, для минимизации ошибки сети (расстояния от входных векторов невязки до выигравших нейронов).

Размерность сети выбрана в соответствии с общей рекомендацией: количество нейронов должно значительно превосходить число классов, которых в данной задаче 21.  

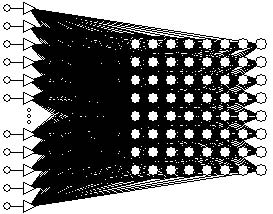
Рис. 5. Сеть Кохонена, использованная для получения наборов евклидовых расстояний до выигравших нейронов

После обучения и верификации сети были получены наборы евклидовых расстояний между векторами невязки ɛ_i и центрами (весовыми векторами) нейроновпобедителей обученной сети. Чтобы удостовериться в нормальности распределения полученных наборов расстояний, соответствующих различным процентам компонентов псевдорешений, выходящих за рамки доверительных интервалов, был использован тест хи-квадрат из пакета программ STATISTICA 8.0. В табл. 2 показаны результаты данной проверки.

Таблица 2. Результаты проверки нормальности полученных наборов расстояний: Chi-Square test – значение статистики

Таблица 2 (продолжение; правая часть таблицы) 

Полученные результаты позволяют считать большинство распределений расстояний нормальными (p³0,05), однако встречаются наборы расстояний, чьи распределения статистически значимо отличаются от нормального (p<0,05). Такой результат может быть объяснен, скорее всего, небольшим количеством векторов невязки (по 64 на каждый процент), сгенерированных для обучения сети, но есть все основания считать (см. центральную предельную теорему), что выборочные распределения наборов расстояний стремятся к нормальным с увеличением количества векторов невязки, входящих в генерируемые наборы. Учитывая, что большинство распределений расстояний являются нормальными, было решено продолжить анализ.

На рис. 6 представлены средние значения расстояний в зависимости от процента случайных компонентов сгенерированных псевдорешений, выходящих за рамки своих доверительных интервалов.

Оценки средних значений и дисперсий полученных наборов идентифицируют полученные распределения и позволяют вычислить вероятность превысить расстояние между вектором невязки псевдорешения ɛ (равное 0,47) и соответствующим центром нейронапобедителя, что делает возможным оценить степень адекватности модели.

Распределение вероятности (как функции от среднего процентного соотношения) превышения расстояния между вектором невязки ɛ и центром нейрона-победителя, полученное при решении данной задачи, показано на рис. 7.

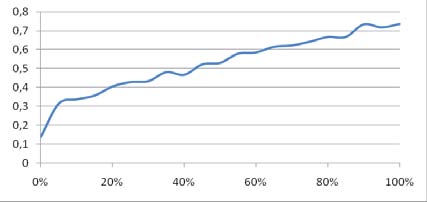
Рис. 6. Средние значения расстояний в зависимости от процента случайных компонентов сгенерированных псевдорешений, выходящих за рамки своих доверительных интервалов

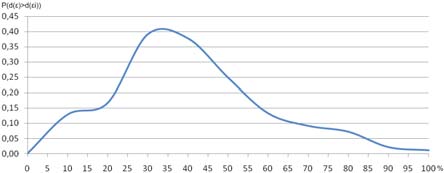
Рис. 7. Распределение вероятности превышения расстояния между наблюдаемым вектором невязки и центром нейрона-победителя как функция от среднего процента
компонентов псевдорешения, выходящих за рамки доверительных интервалов

Данный график распределения вероятности превышения расстояния между наблюдаемым вектором невязки и центром нейрона-победителя строится исходя из нормального распределения полученных расстояний на основе выборочных оценок средних и стандартных отклонений расстояний сгенерированных псевдорешений и имеет пик, соответствующий 35 % компонентов псевдорешения, выходящих за рамки доверительных интервалов. Таким образом, 65 % компонентов лежат в своих доверительных интервалах, что свидетельствует о приемлемом согласовании модели с наблюдениями и позволяет использовать данную модель на практике.

Анализ факторных влияний

Полученные оценки дисперсий факторов модели, позволяющие оценить баланс факторных влияний на наблюдаемые переменные (см. табл. 3), показывают незначительность влияния общего фактора на изменчивость индекса Джини. Однако удаление соответствующих влияний приводит к вырожденности матрицы переопределенной системы уравнений и появлению зависимых переменных, устранение которых вызывает качественное изменение модели. Это позволяет говорить о целесообразности сохранения указанных связей.

Таким образом, новый метод проверки адекватности моделей с помощью самоорганизующихся карт признаков, позволяющий снять с результатов наблюдений ограничения, связанные с их вероятностным распределением, применен на практике.

Оценка степени адекватности предложенной модели дисперсионных составляющих по новому критерию показала, что около 60 % выборочных оценок компонентов псевдорешения лежат в своих доверительных интервалах, что позволяет использовать данную модель на практике.

 Таблица 3. Оценки балансов факторных влияний на изменчивость наблюдаемых переменных²

² Дисперсии общего и специфического факторов указаны в процентах от наблюдаемой дисперсии соответствующей переменной. Из-за наличия невязок сумма дисперсий общего и специфического факторов может не совпадать с наблюдаемой дисперсией.

Используя полученные оценки параметров модели, можно сделать следующие выводы о балансе влияний общего и специфического факторов на каждый показатель, а также об изменении факторных влияний во времени:

1. Изменчивость индекса коррупции: а) доля дисперсии общего фактора в изменчивости показателя коррупции в первом периоде составляет около 17 %;

б) влияние общего фактора на изменчивость показателя коррупции усиливается во втором периоде и составляет уже 44 %. При этом влияние специфического фактора значительно уменьшается (с 87 до 52 %) и появляется доля необъясненной дисперсии (4 %), которая, вероятнее всего, обусловлена новыми факторными влияниями (инновациями), не учтенными в разработанной модели;

в) следует отметить, что специфические факторы E_K3 и E_K4 слабо коррелируют во времени (коэффициент корреляции факторов составляет -0,14). При этом наблюдается средняя корреляция (0,48) между факторами E_K3 и E_U4 и очень высокая отрицательная корреляция (-0,99) между факторами E_K4 и E_U4. Указанное транзитивное соотношение факторов E_K3 и E_K4 свидетельствует об их составном характере, требующем дальнейшей детализации.

2. Изменчивость индекса Джини:

а) влияние общего фактора на изменчивость показателя неравенства доходов по сравнению с влиянием специфического фактора в обоих периодах ничтожно мало: 0 % в первом периоде и 3 % – во втором;

б) изменчивость индекса Джини в основном определяется специфическим фактором E_D, который не изменяет характера своего влияния во времени (коэффициент корреляции данного фактора между первым и вторым периодом составляет 0,99);

в) высокая ошибка при выражении наблюдаемой дисперсии индекса Джини через факторные дисперсии во втором периоде (дисперсия специфического фактора описывает 163 % наблюдаемой дисперсии индекса), а также слабое влияние общего фактора выделяют данный показатель среди остальных: если учесть его стабильность во времени, возникает предположение о значительном влиянии фактора неравенства доходов на остальные показатели;

г) значительный процент необъясненной дисперсии показателя DW₃ в первом периоде (около 64 %) частично опровергает указанное предположение. Однако, обратив внимание на зависимые свободные параметры модели, а именно на корреляцию между факторами E_U3 и E_D4, и учитывая схожее влияние этих факторов (зеркальное) на связанные показатели, можно предположить сильную взаимосвязь данных факторов с некоторой задержкой во времени. Рекомендуется исследовать взаимосвязи общего фактора F с факторами E_U и E_D, а также оценить степень их влияния на все наблюдаемые параметры.

3. Изменчивость показателя убийств:

а) существенное влияние общий фактор оказывает также на изменчивость показателей UW₃ и UW₄ : общий фактор описывает в первом периоде около 28 % наблюдаемой дисперсии, а во втором периоде это влияние уменьшается примерно до 24 %;

б) специфический фактор E_U в первом периоде избыточно описывает изменчивость этого показателя (около 133 % наблюдаемой дисперсии), но во втором периоде это влияние резко уменьшается до 25,5 %. При этом возникает доля необъясненной дисперсии – около 51 %. Очевидно, что изменчивость показателя убийств во втором периоде подвержена новым скрытым влияниям, которые не были учтены в модели. Этот факт представляет интерес для дальнейшего исследования.

Наличие достаточно большого числа выводов относительно баланса влияния факторов на наблюдаемые переменные и относительно взаимодействия факторов требует дополнительной интерпретации специалистами-психологами и социологами. Автор не обладает соответствующими квалификациями и приводит в качестве выводов и результатов работы лишь обнаруженные зависимости, статистически значимые для использованной выборки, приведенного критерия и оговоренных ограничений, но не дает их содержательного толкования. Адекватность полученных результатов должна быть подтверждена содержательной психологической и социологической интерпретацией полученных результатов анализа факторных влияний.

Основные результаты

Разработан и применен на практике новый критерий оценки адекватности факторных моделей в рамках используемой в исследовании выборки, который опирается на возможности самоорганизующихся карт признаков Кохонена и позволяет снять с результатов наблюдений ограничения, связанные с их вероятностным распределением.

Предложенный подход имеет следующие преимущества:

• на наблюдаемые переменные и компоненты вектора невязки не налагается условие многомерной нормальности;
• обеспечивается возможность оценки наиболее вероятного процента статистически значимых отклонений компонентов вектора невязки псевдорешения;
• обеспечивается высокая надежность оценок степени адекватности модели ввиду неограниченного размера генерируемой выборки дисперсий и ковариаций, составляющих псевдорешение.

Автор выражает благодарность доктору психологических наук, члену-корреспонденту РАН, заместителю директора Института психологии РАН Андрею Владиславовичу Юревичу и доктору психологических наук, заведующему лабораторией психологии и психофизиологии творчества Института психологии РАН профессору Дмитрию Викторовичу Ушакову за предоставленные для анализа данные и обсуждение результатов работы, а также доктору технических наук, декану факультета информационных технологий Московского городского психолого-педагогического университета профессору Льву Семеновичу Куравскому – за консультации.

1. Галушкин А. И. Теория нейронных сетей: Учеб. пособие. М.: ИПРЖР, 2000.
2. Добеши И. Десять лекций по вейвлетам. М.: РХД, 2001.
3. Куравский Л. С., Баранов С. Н., Малых С. Б. Нейронные сети в задачах прогнозирования, диагностики и анализа данных. М.: РУСАВИА, 2003.
4. Куравский Л. С., Мармалюк П. А., Абрамочкина В. И., Петрова Е. А. Применение факторного анализа результатов вейвлет-преобразований для исследования динамики психологических характеристик // Экспериментальная психология. 2009 a. Т. 2. № 1. С. 97–111.
5. Куравский Л. С., Мармалюк П. А., Баранов С. Н., Абрамочкина В. И., Петрова Е. А. Факторный анализ результатов вейвлет-преобразований лонгитюдных данных как новый метод исследования динамических характеристик сложных систем // Нейрокомпьютеры: разработка и применение. 2009 b. № 9. С. 5–19.
6. Куравский Л. С., Юревич А. В., Мармалюк П. А., Иванова Е. Г. Факторный анализ показателей нравственного состояния общества в европейских странах // Психологическая наука и образование. 2010. № 1. С. 94–110.
7. Мармалюк П. А. Оценка степени адекватности факторных моделей c помощью самоорганизующихся карт признаков Кохонена // Нейрокомпьютеры: разработка и применение. 2010. № 10. С. 53–62.
8. Нейронные сети. STATISTICA Neural Networks. М.: Горячая линия-Телеком, 2000.
9. Шустенкова Е. В. Множественный вейвлет-анализ в социологии // Вестник общественного мнения: Данные. Анализ. Дискуссии. 2008. Т. 94. № 2. С. 49–59.
10. Юревич А. В. Нравственность как психологическая проблема // Вопросы психологии. 2009. № 4. C. 3–13.
11. Юревич А. В., Ушаков Д. В. Макропсихология как новая область психологических исследований // Вопросы психологии. 2007. № 4. C. 3–15.
12. Kuravsky L. S., Baranov S. N. Development of the wavelet-based confirmatory factor analysis for monitoring of system factors // Proc. 5th International Conference on Condition Monitoring & Machinery Failure Prevention Technologies. Edinburgh, 2008. P. 818–834.
13. Kuravsky L. S., Baranov S. N., Baranov N. I. Wavelet-based confirmatory factor analysis for monitoring of system factors: estimating goodness-of-fit measures with the aid of self-organizing feature maps // Proc. 6th International Conference on Condition Monitoring & Machinery Failure Prevention Technologies. Dublin. 2009. P. 224–245.
14. Loehlin J. C. Latent variable models: An introduction to factor, path, and structural analysis. Hillsdale, NJ: Erlbaum, 1987.