Экспериментальная психология
2016. Том 9. № 3. С. 118–137
doi:10.17759/exppsy.2016090310
ISSN: 2072-7593 / 2311-7036 (online)
Диагностика лётного состава по результатам работы на авиационных тренажерах*
Аннотация
Общая информация
* Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 14-06-00191).
Ключевые слова: видеоокулография, марковская модель, многофакторная сеть Маркова, диагностика, авиационный тренажер, факторный анализ
Рубрика издания: Психология труда и инженерная психология
Тип материала: научная статья
DOI: https://doi.org/10.17759/exppsy.2016090310
Для цитаты: Куравский, Л.С., Мармалюк, П.А., Юрьев, Г.А., Беляева, О.Б., Прокопьева, О.Ю. (2016). Диагностика лётного состава по результатам работы на авиационных тренажерах. Экспериментальная психология, 9(3), 118–137. https://doi.org/10.17759/exppsy.2016090310
Полный текст
КУРАВСКИЙ Л. С.[Барабанщиков, 2008], ГБОУ ВПО МГППУ, Москва, Россия, e-mail: l.s.kuravsky@gmail.com
МАРМАЛЮК П. А.[Барабанщиков, 1997], ГБОУ ВПО МГППУ, Москва, Россия, e-mail: ykk.mail@gmail.com
ЮРЬЕВ Г. А.[Барабанщиков, 2013], ГБОУ ВПО МГППУ, Москва, Россия, e-mail: g.a.yuryev@gmail.com
БЕЛЯЕВА О. Б.[Береговой, 1978], ГБОУ ВПО МГППУ, Москва, Россия,
e-mail: olga95259@yandex.ru
ПРОКОПЬЕВА О. Ю.[Дж.О.Ким, 1989], ГБОУ ВПО МГППУ, Москва, Россия, e-mail: prokopyeva08@mail.ru
В работе представлено описание новой концепции диагностики лётного состава по результатам работы на авиационных тренажерах. Применяемый подход основан на представлении движения взора пилота с помощью марковского процесса с непрерывным временем. Рассматриваются процедуры идентификации прогнозирующей модели, оценки степени адекватности модели наблюдениям и способы построения классификатора, позволяющего количественно оценивать близость испытуемых к эталонам, относящимся к различным диагностируемым группам. Итоговый критерий для оценки лётной квалификации по серии контрольных упражнений формируется на основании интегральных диагностических показателей, которые определяются с помощью параметров идентифицированных моделей. В статье приводится описание эксперимента, иллюстрации и результаты проведенных исследований, направленных на оценку надежности разработанных моделей и критериев, а также формулируются выводы о применимости разработанного подхода в прикладной области, его преимуществах и недостатках.
Введение
В настоящее время системы компьютеризированной диагностики успешно применяются при профессиональном отборе и мониторинге для оценки уровня сформированности знаний, умений и навыков, а также психофизиологического состояния. Их применение способствует повышению объективности, информативности и точности оценок, а также стандартизации и автоматизации измерений. Важнейшей задачей, подходам к решению которой посвящена данная работа, является создание подобных систем для авиационных приложений. Особенно актуальны разработка и исследование новых подходов, применяемых для оценки уровня подготовки лётного состава по результатам работы на современных авиационных тренажерах, где отрабатываются действия в особых условиях полета. Существующие в этой области диагностические средства, как правило, используются для анализа итоговых результатов деятельности, без учета характеристик самой деятельности, и дают достаточно грубые и ненадежные оценки, основанные на искусственных критериях.
Одним из перспективных подходов, позволяющих добиться прогресса в области создания систем компьютеризированной диагностики и преодолеть часть указанных проблем, является использование данных видеоокулографии. Результаты экспериментальных исследований свидетельствуют о наличии факторов, существенно влияющих на изменчивость показателей глазодвигательной активности в рамках фиксированного стимульного материала и определяющих пространственно-временные особенности траекторий взора в гомогенных (по уровню выраженности фактора) группах испытуемых (Барабанщиков, 1997; 2008; Барабанщиков, Жегалло, 2013). К настоящему времени выявлен достаточно представительный список показателей такого рода, в которых проявляются значимые различия для диагностируемых категорий испытуемых (Барабанщиков, Жегалло, 2013).
Анализ накопленных авторами наблюдений выявил, что характеристики, представляющие интерес для фундаментальных исследований и традиционно исследуемые при обработке результатов видеоокулогафии, такие как саккады, фиксации и построенные на их основе более сложные зависимости, включая карты распределения внимания («тепловые карты»), могут быть недостаточны для построения эффективных формализованных процедур диагностики. В таких случаях для успешного решения задачи диагностики целесообразно использование многомерных моделей представления объекта анализа, учитывающих динамические свойства процесса, а также показателей, основанных на параметрах этих моделей, идентифицированных для различных групп испытуемых.
Один из вариантов такого решения представлен в данной работе, где рассмотрены:
- новая концепция диагностики лётного состава по результатам работы на авиационных тренажерах, основанная на представлении движения взора пилота с помощью случайного марковского процесса с непрерывным временем;
- процедура идентификации и оценки адекватности прогнозирующих моделей;
- способы построения классификатора, позволяющего оценивать степень соответствия испытуемых эталонам, относящимся к различным диагностируемым группам;
- интегральные количественные диагностические показатели, позволяющие строить итоговый критерий для оценки лётной квалификации по серии контрольных упражнений.
Подробное математическое обоснование основ разработанного подхода дано в статьях (Куравский и др., 2012; Куравский, 2013; Kuravsky et al., 2015a; 2015b; 2015c; 2016).
В рамках деятельностного и системного подходов (Барабанщиков,1997; Барабанщиков, Жегалло, 2013; Леонтьев, 1979; Ломов, 1975), принятых в современной отечественной психологии, следует регистрировать и оценивать следующие характеристики, составляющие так называемую модель деятельности (Береговой и др., 1978; Обознов, 2003):
- данные видеоокулографии;
- параметры воздействия на органы управления летательного аппарата (ЛА);
- параметры движения ЛА, полученные в результате воздействий на его органы управления (результат деятельности).
Очевидно, что последние два компонента данной модели требуют экспериментов с нереальным объемом финансовых и организационных затрат. Кроме того, отсутствуют приемлемые модели и критерии для оценки как корректности воздействий на органы управления ЛА, так и параметров его движения. Единственным формальным нормативом, имеющим юридическую силу, является Руководство по лётной эксплуатации (1994), которое фиксирует только допустимые диапазоны параметров для различных режимов полета и не может обеспечить релевантную оценку навыков пилотирования и, тем более, психофизиологического состояния. В результате сложилась практика, согласно которой такие оценки носят экспертный характер и обеспечиваются пилотом-инструктором. Поэтому оценки воздействий на органы управления ЛА и корректности параметров его движения, используемые при моделировании деятельности пилотов, целесообразно заменять соответствующими экспертными заключениями, что и сделано в данной работе. Это существенно снижает уровень затрат на проведение экспериментов, упрощает указанную модель и, в целом, делает решаемой поставленную задачу.
Другим аргументом в пользу указанного выше подхода является то, что создание моделей и критериев для оценки воздействий на органы управления ЛА и параметров его движения есть задача, намного более сложная, чем исходная. Поэтому использование модели деятельности без упрощений, связанных с экспертными заключениями, приводит к замене относительно простой задачи более сложной и заводит решение в тупик.
Важно отметить, что под диагностикой лётного состава в этой работе понимается исключительно выявление окулографических маркеров, свидетельствующих о недостатке необходимых навыков пилотирования или неблагополучном психофизиологическом состоянии, более широко задача не ставится.
В этой работе представлены результаты экспериментов, которые проводились в авиационном учебном центре в г. Пушкино Московской области силами специалистов факультета информационных технологий Московского городского психолого-педагогического университета, центра экспериментальной психологии того же университета, учебного центра ФБУ «Авиалесохрана», авиакомпании «ЛУКОЙЛ-АВИА» и ООО «Русское авиационное общество» на базе учебно-тренировочного комплекса вертолета Ми-8МТВ-1, обеспечивающего полный цикл подготовки лётного состава и включающего комплексный тренажер, автоматизированную систему обучения, комплекс моделирования тактической обстановки и рабочее место системы объективного контроля (рис. 1). Контрольные упражнения выполняли экипажи вертолетов ООО «ЛУКОЙЛ-АВИА» с различными уровнями лётной подготовки. Несмотря на относительно небольшое число экипажей, участвовавших в исследовании, полученные результаты позволяют сделать полезные для практики и значимые в научном отношении выводы, приведенные в последующих разделах этой работы.
1. Диагностический критерий на основе вероятностных моделей и оценок
правдоподобия
1.1. Постановка задачи диагностики и этапы ее решения
Полагается, что экипаж летательного аппарата выполняет на авиационном тренажере определенное контрольное задание (далее - упражнение):
— упражнение E1: полет по кругу, частичный отказ двигателя при наборе высоты, отказ путевого управления в районе первого разворота;
— упражнение E2: прерванный взлет, отказ основной гидросистемы, отказ двигателя при разгоне до высоты 50 м, зима, снежный вихрь, нижняя граница области 100 м;
— упражнение E3: полет по кругу, облачность, нижняя граница облачности - 100 м, снежный вихрь, ветер;
— упражнение E4: полет по кругу, зима, слабый снег, полет в облаках, нижняя граница облачности - 100 м;
— упражнение E5: заход по приборам на посадку, ночь, снежный вихрь, нижняя граница облачности - 100 м, высота - 200 м.
При этом известна принадлежность экипажей к группам (категориям), отражающим уровень лётной подготовки. Полагая, что для каждой из этих групп доступна соответствующая выборка наблюдаемых траекторий движения взора командира воздушного судна (КВС) по поверхности приборной доски и окну кабины, фиксируемых через равные временные интервалы средствами видеоокулографии, ставится задача распознавания группы, к которой принадлежит вновь наблюдаемый экипаж. Классификация в указанной постановке обеспечивается решением рассмотренных далее следующих подзадач:
— разделения области движений взора, включающей поверхность приборной доски и окна кабины, на ячейки прямоугольной сетки (рис. 2), каждой из которых ставится в соответствие свое состояние марковской модели, в котором взор КВС может находиться с некоторой вероятностью, переходя из одного состояния в другое по определенным правилам;
— расчета выборочных частот пребывания в состояниях марковской модели по выборке траекторий движения взора КВС для каждой диагностируемой группы экипажей в заданные моменты времени;
— идентификации (аппроксимации) временной динамики распределений вероятностей пребывания в состояниях марковской модели по полученным выборочным частотам для всех диагностируемых групп экипажей;
— расчета и сравнения вероятностных оценок правдоподобия наблюдаемой траектории движения взора КВС, зарегистрированной для неидентифицированного экипажа, для каждой из заданных диагностируемых групп;
— выбора наиболее правдоподобной группы экипажей и оценки надежности принятого решения.
Для описания того, как вероятности пребывания траектории движения взора в заданных дискретных состояниях изменяются с непрерывным временем, применяются двумерные сети Маркова (Куравский, Баранов, Корниенко, 2005; Куравский и др., 2013; Kuravsky, Baranov, 2005; Kuravsky et al., 2015d). По результатам накопленных наблюдений проводится прогнозирование указанных вероятностей с использованием параметрических математических моделей, описываемых марковскими случайными процессами с дискретными состояниями и непрерывным временем (Куравский, Юрьев, 2012; Куравский, Баранов, Корниенко, 2005; Куравский, Марголис, Юрьев, 2008; Куравский и др., 2012; Куравский, Юрьев, 2011; Kuravsky, Malykh, 2000; 2004).
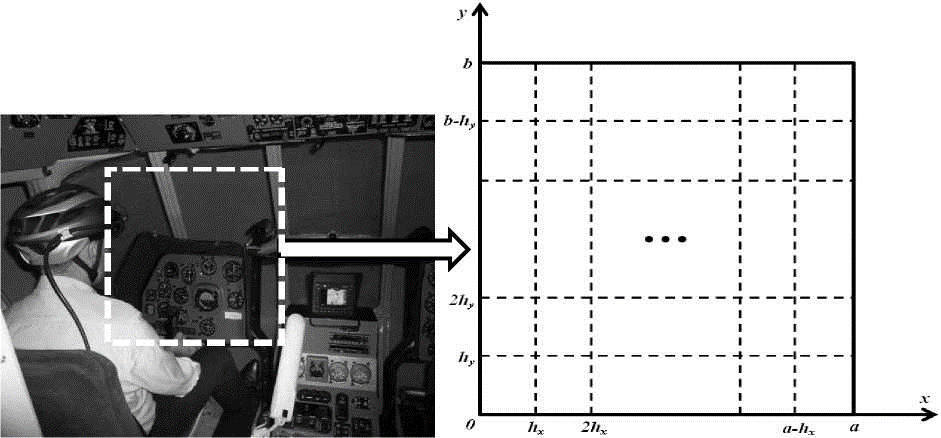
Рис. 2. Дискретизация области движений взора прямоугольной сеткой
1.1. Представление модели
Марковская модель для описания динамики переходов между состояниями процесса представляется ориентированным графом, в котором вершины соответствуют состояниям, а дуги - возможным переходам между выделенными состояниями (рис. 3). Процесс переходов между состояниями может рассматриваться как случайное блуждание по графу из одного состояния в другое согласно направлениям дуг. Переходы между состояниями мгно- венны и происходят в случайные моменты времени, а частоты переходов между состояниями зависят от величин свободных параметров модели - интенсивностей переходов между
-состояниями рассматриваемого случайного процесса i = L .. К .
1.2. Идентификация модели
Следуя представленному в работах (Куравский и др., 2012; Куравский, 2013; Kuravsky et al., 2015) методу решения диагностической задачи, необходимо, используя данные наблюдений, решить подзадачу идентификации распределений вероятности пребывания взора в ячейках дискретизованной области движения взора для всех диагностируемых групп экипажей. Аппроксимация этих распределений с учетом проведенной дискретизации сводится к оценке интенсивностей переходов между состояниями рассматриваемого случайного процесса . ..„..
Для решения задачи идентификации выполняется численная процедура многомерной нелинейной оптимизации, обеспечивающая решение обратной задачи для системы дифференциальных уравнений Колмогорова (Куравский, 2013; Kuravsky et al., 2015a). В результате ее решения находится набор свободных параметров, который определяет систему уравнений, решение которой обладает заданными характеристиками (вероятностные функции времени, аппроксимирующие наблюдаемую динамику вероятностей пребывания взора в ячейках дискретизованной области).
Оценки свободных параметров (интенсивностей переходов) могут быть определены с опорой на критерий соответствия наблюдаемых и прогнозируемых гистограмм, описываю- щих распределения частот пребывания в состояниях процесса. В качестве такого критерия далее используется статистика Пирсона:
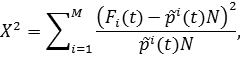
Такой способ идентификации свободных параметров называется методом минимума χ2 (Крамер, 1976). Согласно теореме Крамера (Крамер, 1976), при выполнении ряда общих условий, в случае адекватности модели случайного процесса наблюдениям, рассмотренная задача иденти- фикации имеет единственное решение, которое сходится по вероятности к искомому решению, а значения статистики X2 асимптотически описываются распределением χ2 с M–γ–1 степенями сво- боды, где γ – число определяемых значений свободных параметров. Знание распределения позво- ляет использовать приведенную выше статистику для проверки гипотезы о том, что полученные прогнозируемые частоты попадания в состояния согласуются с результатами наблюдений.
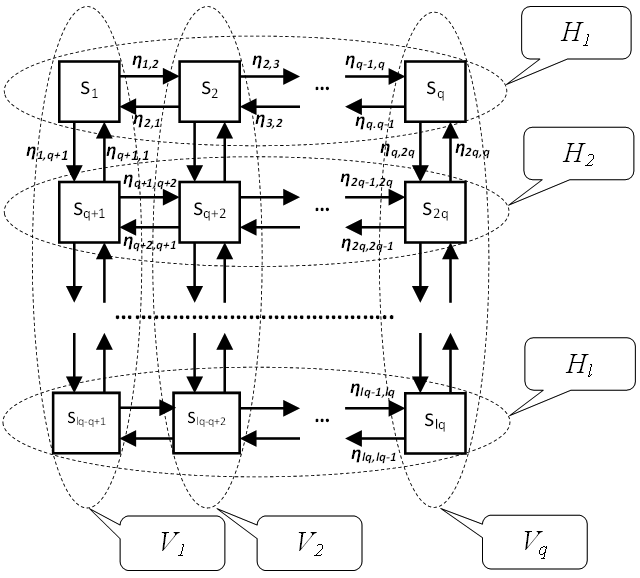
Для этого строки и столбцы состояний исходной сети могут быть объединены в сгруп- пированные состояния, а именно: нахождение в состоянии Vj (j=1,2,…,q) равносильно на- хождению в одном из состояний sj, sj+q, …, sj+(l-1)q, а нахождение в состоянии Hi (i=1,2,…,l) рав- носильно нахождению в одном из состояний s(i-1)q+1, s(i-1)q+2, …, siq. Таким образом, исследо- вание исходного случайного процесса, структура связей состояний которого определяется прямоугольной сеткой размерностью (рис. 3), сводится к анализу двух процессов со сгруппированными состояниями, имеющих меньшую размерность (l или q) и упрощенную структуру связей (рис. 4 и 5).
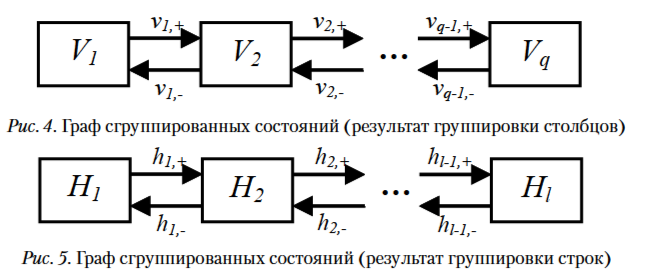
Интенсивности переходов между сгруппированными состояниями могут быть идентифицированы, как указано выше. Возврат к исходному процессу прост: полагая, что вероятности пребывания в вертикально и горизонтально расположенных группах состояний независимы, вероятность нахождения в состоянии, одновременно принадлежащем группам Hi и Vj, вычисляется как произведение вероятностей ;.' и р/. пребывания в этих группах.
Поскольку вероятность пребывания в каждом из сгруппированных состояний равна сумме вероятностей пребывания в составляющих его состояниях исходного случайного процесса, уравнения Колмогорова для вероятностей нахождения взора в сгруппированных состояниях получаются путем согласованного суммирования левых и правых частей всех уравнений, которые соответствуют ячейкам, формирующим данные состояния:
1.5. Классификация траекторий на основе оценок правдоподобия
Получив, как показано выше, аппроксимации распределений вероятностей пребывания взора в ячейках дискретизованной области для различных групп испытуемых = i’j , можно определять вероятностные оценки принадлежности к заданным категориям ранее неидентифицированных лиц. Чтобы решить эту задачу, для каждого такого лица следует зарегистрировать траекторию движения взора по поверхности приборной доски и окну кабины U(t) и, используя заранее известные аппроксимации указанных распределений, определить оценки правдоподобия прохождения наблюдаемых траекторий. В общем случае для каждой категории п: при этом вычисляется криволинейный интеграл 1-го рода:
1.5. Пример результатов моделирования
В качестве иллюстрации, на рис. 6 и 7 приведены траектории движения и идентифицированные распределения вероятностей пребывания взора в области, включающей поверхность приборной доски и окно кабины, при выполнении экипажами С1 и С4 упражнения E5. Запись движений глаз проводилась с помощью мобильной системы регистрации движений глаз SMI iView X HED (рис. 2) в монокулярном режиме с частотой 50 Гц. Регистрирующие компоненты этой системы фиксировалась на голове КВС и не стесняли движений. Регистрация данных проводилась без фиксации головы пилота. Калибровка выполнялась стандартным способом с использованием пяти опорных точек на приборной доске. Наблюдаемая испытуемым сцена фиксировалась с помощью фронтальной видеокамеры. Распределения вероятностей пребывания взора представлены для одних и тех же трех контрольных моментов времени.
В табл. 1 представлены оценки правдоподобия траекторий движения взора КВС экипажа C1 для упражнений E1-E5. Во всех пяти случаях траектория, зарегистрированная в конкретном упражнении, оказывалась наиболее правдоподобной для модели, идентифицированной по данным этого же упражнения, что подтверждает корректность вычисленных оценок.
Таблица 1
Оценки правдоподобия траекторий движения взора КВС экипажа C1
для упражнений E1-E5
|
|
Модель |
|||||
|
E1 |
E2 |
E3 |
E4 |
E5 |
||
|
Траектория |
E1 |
-126,138 |
-162,984 |
-209,016 |
-228,157 |
-276,688 |
|
E2 |
-204,266 |
-122,373 |
-175,239 |
-251,365 |
-222,686 |
|
|
E3 |
-155,088 |
-153,128 |
-116,418 |
-269,201 |
-229,436 |
|
|
E4 |
-159,787 |
-156,939 |
-169,511 |
-117,716 |
-173,093 |
|
|
E5 |
-213,87 |
-200,727 |
-237,136 |
-222,94 |
-179,962 |
|
2. Диагностический критерий на основе вероятностных моделей и интегральных
оценок их параметров
Как указано во введении, использование традиционных характеристик, распространенных в айтрекинговых исследованиях, может не дать дифференциации, необходимой для построения диагностических оценок. Подход, использующий марковские модели и оценки правдоподобия, рассмотренный в разделе 1, такую дифференциацию обеспечивает, однако требует накопления значительного объема экспериментальных данных, что затрудняет его практическое применение.
В этом разделе предлагается подход, опирающийся на интегральные оценки параметров рассмотренных ранее вероятностных моделей. Его преимуществами являются:
- отсутствие жесткой привязки к пространственному расположению приборов, находящихся в поле зрения пилота, и, соответственно, к типу летательного аппарата;
- меньший объем экспериментальных данных, необходимых для корректной диагностики;
- невысокие требования к точности регистрации траектории движения взора, что существенно при проведении экспериментов и диагностических процедур в «полевых» условиях.
Основными диагностическими характеристиками являются идентифицированные для рассмотренных ранее моделей оценки наибольших интенсивностей переходов, в вертикальном и горизонтальном направлениях. Этот выбор обусловлен:
- выявленными в результате экспериментов зависимостями продолжительностей и частот фиксаций взора от опыта испытуемых в решении поставленной задачи и наличия у них затруднений при переработке информации (Барабанщиков, Жегалло, 2013);
- зависимостями продолжительности, скорости и частоты саккад от присутствия психиатрических и нейрофизиологических расстройств у испытуемых и приема ими медикаментов и алкоголя (Барабанщиков, Жегалло, 2013).
Поскольку область движения взора, охватывающая приборную доску и стекло кабины, ограничена, интенсивности переходов «вправо-влево» и «вверх-вниз» имеют, как правило, сопоставимые наибольшие интенсивности переходов между состояниями в противоположных направлениях, что подтверждается результатами обработки полученных данных.
Связь указанной характеристики со степенью сформированности навыков пилотирования и психофизиологическим состоянием пилотов очевидна, поскольку неудовлетворительные показатели, обусловленные указанными факторами, приводят к увеличению продолжительности фиксаций взора на приборах, затруднениям в переработке считываемой с них информации и увеличению продолжительности саккад (Барабанщиков, Жегал- ло, 2013). Неподготовленный пилот затрачивает значительное время на оценку показаний приборов; если обстановка требует частого переключения между задачами, он вынужден прерывать процесс анализа их показаний, а затем вновь к нему возвращаться. Такой «возвратный» характер движения взора очевидным образом способствует увеличению интенсивностей переходов между состояниями представленных выше моделей.
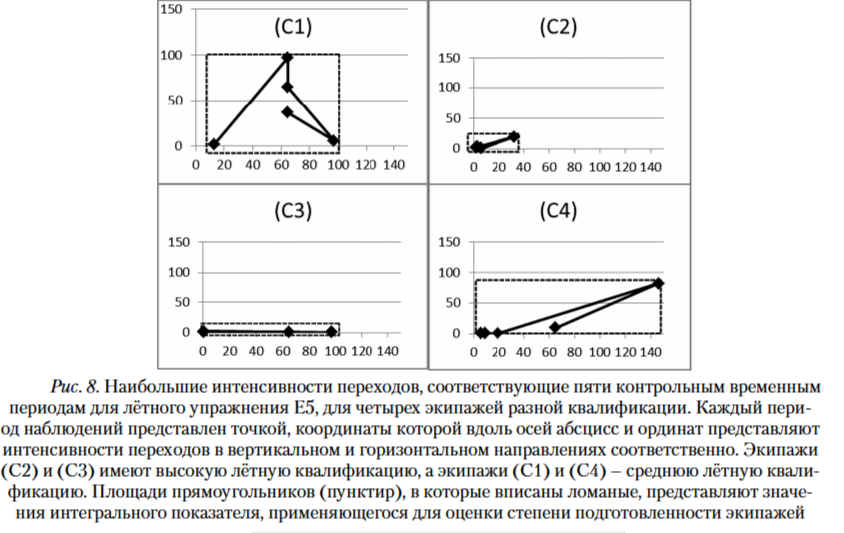
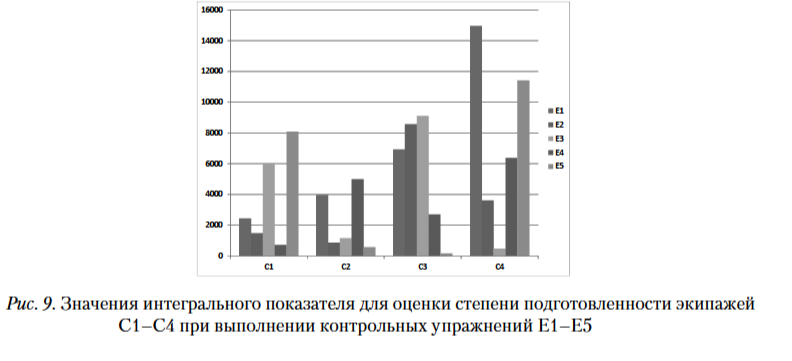
Диаграммы на рис. 8 показывают соотношения наибольших интенсивностей переходов между состояниями двумерных марковских моделей в вертикальном и горизонтальном направлениях, соответствующих пяти контрольным временным периодам наблюдений. Данные, на основе которых построены оценки этих характеристик, получены при выполнении лётного упражнения E5 для четырех экипажей разной квалификации, принимавших участие в экспериментах. Диаграммы демонстрируют очевидную тенденцию к уменьшению приведенных интенсивностей с повышением уровня квалификации экипажа. Поскольку вертикальное и горизонтальное направления практически равноценны при принятии диагностических решений, может быть получен удобный интегральный показатель, позволяющий сформулировать решающее правило для оценки квалификации экипажей. Вычислительные эксперименты с различными видами комбинаций этих параметров показали, что произведение наибольших интенсивностей переходов в вертикальном и горизонтальном направлениях является оптимальным для данной задачи. Графически эта характеристика представляется площадями пунктирных прямоугольников (рис. 8). Значения этой величины для различных экипажей и контрольных упражнений показаны на рис. 9. Легко заметить, что упражнение E5 (заход ночью по приборам на посадку) обеспечивает наилучшую дифференциацию экипажей.
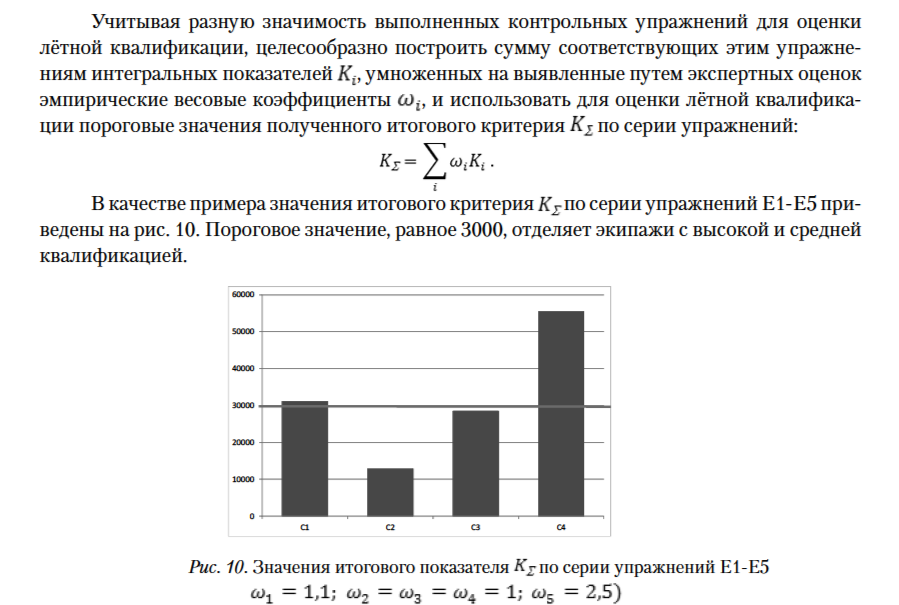
Альтернативой оценке лётной квалификации на основе итогового показателя А^ является классификация экипажей с помощью вероятностных нейронных сетей.
На вход распознающей сети в таком случае подаются упорядоченные наборы наибольших интенсивностей переходов для заданных временных периодов. Каждому обучающему наблюдению во внутреннем слое сети соответствует один элемент на радиальных базисных функциях (радиальный элемент), функция активации которого представляет собой функцию Гаусса с центром в данном наблюдении.
Число элементов во внутреннем слое такой сети определяется числом наблюдений, а число элементов в выходном слое - числом распознаваемых групп. Вероятностная нейронная сеть не требует обучения и может динамически пополняться новыми радиальными элементами по мере накопления наблюдений.
Как правило, целесообразно иметь свою распознающую вероятностную нейронную сеть для каждого контрольного упражнения.
В целом, представленные в этом разделе результаты позволяют говорить об эффективности рассмотренного подхода и возможности построения на его основе автоматизированных диагностических средств оценки уровня подготовки лётного состава по результатам работы на авиационных тренажерах.
3. Оценка баланса влияния навыков пилотирования и психофизиологического состояния экипажа на исследуемые характеристики
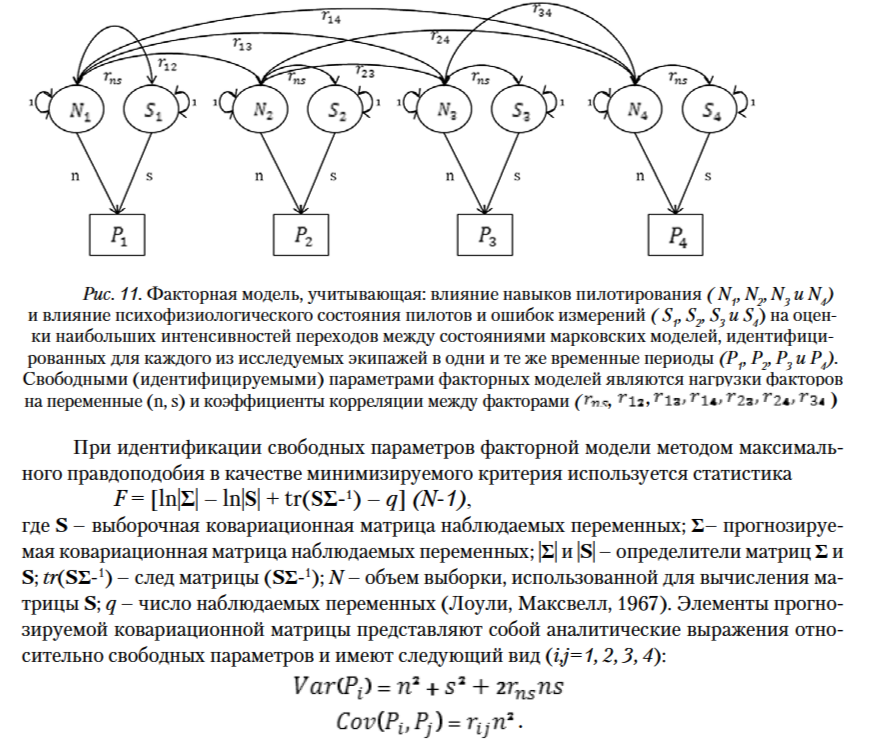
Для оценки баланса влияния навыков пилотирования и психофизиологического состояния экипажа на исследуемые характеристики применен факторный анализ (Ким, Мьюллер, Клекка, 1989; Куравский и др., 2011; Лоули, Максвелл, 1967). В факторной модели, представленной в виде путевой диаграммы на рис. 11, учитываются факторы влияния навыков пилотирования, психофизиологического состояния пилотов, а также ошибки измерений. В качестве наблюдаемых переменных используются рассмотренные выше оценки интенсивностей переходов, идентифицированные для каждого из экипажей.
В предположении о многомерном нормальном распределении рассматриваемых наблюдаемых переменных значения критерия F описываются распределением χ2.
Для идентификации свободных параметров необходимо численно решить достаточно трудоемкую задачу локальной многомерной оптимизации. Альтернативные процедуры идентификации рассмотрены в работах (Куравский, Баранов, Корниенко, 2005; Куравский и др., 2011; Kuravsky et al., 2015a).
Для устранения статистически незначимых компонентов полной модели, представ- ленной на рис. 11, и выявления ее структуры, оптимальной с точки зрения соответствия на- блюдениям, сопоставлялись:
– полная модель;
– упрощенная модель, не имеющая корреляций между парами факторов Ni и Si (i=1, 2, 3, 4);
-упрощенная модель, не имеющая факторов Ni (i=1, 2, 3, 4).
Результаты сопоставления показаны в табл. 2. Производилась проверка гипотезы о том, что построенные факторные модели согласуются с результатами наблюдений.
Выборочные оценки значимости корреляций между наблюдаемыми переменными показали, что корреляции r12, r13, r14 и r23 значимо не отличаются от нуля, что позволило уда- лить их из списка свободных параметров.
|
Модель |
Статистика F |
Число степеней свободы %2 |
p-значение |
Статистическая значимость упрощения модели |
|
Полная модель |
11,97 |
5 |
0,035 |
- |
|
Упрощенная модель без корреляций между парами факторов N и S (i=1,2,3,4) ’ ’ |
11,97 |
6 |
0,06 |
Различия в значениях статистики F при 1-й ст. св. статистически значимыми не являются |
|
Упрощенная модель без факторов Ni (i=1,2,3,4) |
14,64 |
7 |
0,04 |
Различия в значениях статистики F при 2-й ст. св. статистически значимыми не являются |
Как видно из табл. 2, гипотеза о согласовании с результатами наблюдений полной факторной модели отвергается при уровне значимости 0,05 (p<0,05).
Та же гипотеза при том же уровне значимости для упрощенной модели без корреляций между парами факторов Ni и Si (i=1, 2, 3, 4) отвергнута быть не может (p>0,05). Разность статистик F для полной и упрощенной моделей асимптотически распределена как х2 с числом степеней свободы, равным разности в числах степеней свободы полной и упрощенной моделей. Этой разности соответствует p-значение, близкое к 1, что позволяет говорить о том, что сделанное в модели упрощение не приводит к значимому изменению статистики F.
Гипотеза о согласовании с результатами наблюдений упрощенной факторной модели без факторов Ni (i=1, 2, 3, 4) отвергается при уровне значимости 0,05 (p<0,05). Проведя те же рассуждения, что и для предыдущей модели, можно прийти к аналогичному выводу относительно значимости изменений статистики F.
Таким образом, оптимальной с точки зрения соответствия наблюдениям следует признать упрощенную модель без корреляций между парами факторов Ni и Si (i=1, 2, 3, 4). Поскольку rns=0, то дисперсия наблюдаемых переменных состоит из двух компонентов (n2 и s2), представляющих соответственно вклады фактора навыков пилотирования и фактора, представляющего совместное влияние психофизиологического состояния пилотов и ошибок измерений. Значения n и s, идентифицированные для указанной оптимальной модели, позволяют говорить о том, что представленная дисперсией изменчивость наблюдаемых параметров на 46% обусловлена влиянием навыков пилотирования и на 54% - совместным влиянием психофизиологического состояния пилотов и ошибок измерений. Это позволяет говорить о сопоставимом влиянии исследуемых факторов на анализируемые характеристики.
Основные результаты и выводы
1. Разработана новая концепция диагностики лётного состава по данным видеоокуло- графии, зарегистрированным во время работы на авиационных тренажерах, которая предполагает использование в качестве основной анализируемой характеристики идентифицированных оценок наибольших интенсивностей переходов между состояниями марковских моделей, представляющих движение взора пилота по поверхности приборной доски и окну кабины. Рассмотренная диагностика сводится к выявлению окулографических маркеров, свидетельствующих о недостатке необходимых навыков пилотирования или неблагополучном психофизиологическом состоянии.
2. Преимуществами представленной концепции являются: отсутствие жесткой привязки к пространственному распределению приборов, меньший объем экспериментальных данных, необходимых для корректной диагностики, и сравнительно низкие требования к точности регистрации траектории движения взора, что существенно в «полевых» условиях.
3. Рассмотренный в данной работе подход, использующий вероятностные модели, обеспечивает дифференциацию, достаточную для построения диагностических оценок, чего не может дать традиционный анализ простейших показателей окуломоторной активности.
4. Проведенные вычислительные эксперименты выявили, что наибольшую дифференциацию для экипажей с разным уровнем подготовки обеспечивает произведение наибольших интенсивностей переходов в вертикальном и горизонтальном направлениях, что позволило вывести простой интегральный показатель для оценки лётной квалификации.
5. Анализ факторных влияний на наибольшие интенсивности переходов между состояниями двумерных марковских моделей, идентифицированные для каждого из исследуемых экипажей в одни и те же временные периоды, выявил, что представленная дисперсией изменчивость указанных параметров на 46% обусловлена влиянием навыков пилотирования и на 54% - совместным влиянием психофизиологического состояния пилотов и ошибок измерений, что позволяет говорить о сопоставимом влиянии исследуемых факторов на анализируемые характеристики.
6. Полученные экспериментальные и расчетные результаты позволяют говорить об эффективности рассмотренного подхода и возможности построения на его основе автоматизированных диагностических средств для оценки уровня подготовки лётного состава по результатам работы на авиационных тренажерах
[Барабанщиков, 2008] Куравский Л. С. Доктор технических наук, профессор, декан факультета информационных технологий, ГБОУ ВПО МГППУ. E-mail: l.s.kuravsky@gmail.com
[Барабанщиков, 1997] Мармалюк П. А.Кандидат технических наук, доцент, факультет информационных технологий, ГБОУ ВПО МГППУ. E-mail: ykk.mail@gmail.com
[Барабанщиков, 2013]Юрьев Г. А. Кандидат физико-математических наук, доцент, факультет информационных технологий, ГБОУ ВПО МГППУ. E-mail: g.a.yuryev@gmail.com
[Береговой, 1978]Беляева О. Б. Студентка, факультет информационных технологий, ГБОУ ВПО МГППУ. E-mail: olga95259@yandex.ru
[Дж.О.Ким, 1989] Прокопьева О. Ю. Магистрант, факультет информационных технологий, ГБОУ ВПО МГППУ. E-mail: prokopyeva08@mail.ru
Литература
- Барабанщиков В.А. Восприятие индивидуально-психологических особенностей человека по изобра- жению целого и частично открытого лица // Экспериментальная психология. 2008. Т. 1. № 1. C. 62–83.
- Барабанщиков В.А. Окуломоторные структуры восприятия. М.: ИП РАН, 1997. 384 с.
- Барабанщиков В.А., Жегалло А.В. Регистрация и анализ направленности взора человека. М.: ИП РАН, 2013. 316 с.
- Береговой Г.Т., Завалова Н.Д., Ломов Б.Ф., Пономаренко В.А. Экспериментально-психологические исследования в авиации и космонавтике. М.: Наука, 1978. 303 с.
- Дж.О.Ким, Мьюллер Ч.У., Клекка У.Р. Факторный, дискриминантный и кластерный анализ. М.: Фи- нансы и статистика, 1989. 215 с.
- Крамер Г. Математические методы статистики. М.: Мир, 1976. 648 с.
- Куравский Л.С., Юрьев Г.А. Вероятностный метод фильтрации артефактов при адаптивном тести- ровании // Экспериментальная психология. 2012. Т. 5. № 1. С. 119–131.
- Куравский Л.С., Баранов С.Н., Корниенко П.А. Обучаемые многофакторные сети Маркова и их при- менение для исследования психологических характеристик // Нейрокомпьютеры: разработка и при- менение. 2005. № 12. С. 65–76.
- Куравский Л.С., Марголис А.А., Юрьев Г.А. Принципы программной реализации психологического тренажера // Психологическая наука и образование. 2008. № 5. С. 182–188.
- Куравский Л.С., Марголис А.А., Юрьев Г.А., Мармалюк П.А. Концепция системы поддержки при- нятия решений для психологического тестирования // Психологическая наука и образование. 2012. № 1. С. 56–65.
- Куравский Л.С., Мармалюк П.А., Алхимов В.И., Юрьев Г.А. Математические основы нового подхо- да к построению процедур тестирования // Экспериментальная психология. 2012. Т. 5. № 4. С. 75–98.
- Куравский Л.С., Мармалюк П.А., Барабанщиков В.А., Безруких М.М., Демидов А.А., Иванов В.В., Юрьев Г.А. Обучаемые структуры как основа программного обеспечения для диагностики навыков и компетенций // Нейрокомпьютеры: разработка и применение. 2013. № 5. С. 46–60.
- Куравский Л.С., Мармалюк П.А., Юрьев Г.А., Баранов С.Н., Полещук Г.Н., Смирнов А.А., Шишов А.Н. Диагностика лётного состава по результатам работы на авиационных тренажерах // Нейрокомпьюте- ры: разработка, применение. № 10. С. 14–23.
- Куравский Л.С., Ушаков Д.В., Мармалюк П.А., Панфилова А.С. Исследование факторных влияний на развитие психологических характеристик с применением нового подхода к оценке адекватности моделей наблюдениям // Информационные технологии. 2011. № 11. С.67–77.
- Куравский Л.С., Юрьев Г.А. Адаптивное тестирование как марковский процесс: модели и их иден- тификация // Нейрокомпьютеры: разработка и применение. 2011. № 2. С. 21–29.
- Куравский Л.С., Юрьев Г.А. Использование марковских моделей при обработке результатов тести- рования // Вопросы психологии. 2011. № 2. С. 112–120.
- Леонтьев А.Н. Категория деятельности в современной психологии // Вопросы психологии. 1979. № 3. С. 11–15.
- Ломов Б.Ф. О системном подходе в психологии // Вопросы психологии. 1975. № 2. С. 31–45.
- Лоули Д., Максвелл А. Факторный анализ как статистический метод. М.: Мир, 1967. 144 с.
- Марковские модели в задачах диагностики и прогнозирования: учеб. пособие / Под ред. Л.С. Ку- равского. М.: РУСАВИА, 2013. 172 с.
- Руководство по лётной эксплуатации вертолета Ми-8МТВ. М.: Министерство транспорта РФ, 1994.
- Обознов А.А. Психическая регуляция операторской деятельности (в особых условиях рабочей сре- ды). М.: ИП РАН, 2003. 184 с.
- Kuravsky L.S., Malykh S.B. Application of Markov models for analysis of development of psychological characteristics // Australian Journal of Educational & Developmental Psychology. 2004. Vol. 2. P. 29–40.
- Kuravsky L.S., Malykh S.B. On the application of queuing theory to analysis of twin data // Twin Re- search. 2000. Vol. 3. P. 92–98.
- Kuravsky L.S., Baranov S.N. The concept of multifactor Markov networks and its application to forecasting and diagnostics of technical systems // Proc. Condition Monitoring 2005. Cambridge, United Kingdom. P. 111–117.
- Kuravsky L.S., Marmalyuk P.A., Baranov S.N., Yuryev G.A. Monitoring of flight crew condition using oculomotor activity measurements // Proc. 12th International Conference on Condition Monitoring & Machinery Failure Prevention Technologies, Oxford. UK. June 2015a. P. 8.
- Kuravsky L.S., Marmalyuk P. A., Yuryev G. A., Dumin P. N. A Numerical Technique for the Identification of Discrete-State Continuous-Time Markov Models // Applied Mathematical Sciences. 2015b. Vol. 9. № 8. P. 379–391. doi: https://doi.org/10.12988/ams.2015.410882
- Kuravsky L.S., Marmalyuk P. A., Yuryev G. A., Dumin P. N., Panfilova A. S. Probabilistic Modeling of a Testing Procedure // Applied Mathematical Sciences. 2015c. Vol. 9. № 82. P. 4053–4066. doi: http://dx.doi. org/10.12988/ams.2015.53234.
- Kuravsky L.S., Marmalyuk P.A., Baranov S.N., Alkhimov V.I., Yuryev G.A, Artyukhina S. V. A New Tech- nique for Testing Professional Skills and Competencies and Examples of its Practical Applications // Applied Mathematical Science. 2015d. Vol. 9. № 21. P. 1003–1026. doi: https://doi.org/10.12988/ ams.2015.411899
- Kuravsky L. S., Marmalyuk P. A., Yuryev G. A., Belyaeva O. B., Prokopieva O. Yu. Mathematical Foun- dations of Flight Crew Diagnostics Based on Videooculography Data // Applied Mathematical Sciences. 2016. Vol. 10. № 30. P. 1449–1466. doi: https://doi.org/10.12988/ams.2015.411899
Информация об авторах
Метрики
Просмотров web
За все время: 2635
В прошлом месяце: 16
В текущем месяце: 7
Скачиваний PDF
За все время: 966
В прошлом месяце: 1
В текущем месяце: 4
Всего
За все время: 3601
В прошлом месяце: 17
В текущем месяце: 11