Сравнительный анализ двух новых концепций адаптивного обучения

В случае традиционного обучения эти проблемы обычно разрешаются в ходе взаимодействия обучающегося с квалифицированным преподавателем, который, ориентируясь на свой субъективный опыт, формирует такие траектории с допустимой учебным процессом степенью индивидуализации, контролируя все этапы передачи знания. Такая работа, как правило, не поддается автоматизации и является своего рода искусством. Следует отметить, что указанное построение индивидуальных траекторий требует в той или иной форме решения диагностических задач (Кибзун и др., 2008, 2012), которые обеспечивают выявление особенностей и возможностей обучающихся, ограничивая тем самым выбор доступных педагогических приемов.

Задача автоматизации адаптивного обучения неформализуемым умениям и навыкам к настоящему времени не имела удовлетворительного решения. Существующие средства организации электронного обучения (Осипов и др., 2007; Сологуб, 2012), включая системы управления обучением и учебным контентом, обходят рассматриваемую проблему, решая более доступные обобщенные задачи организации учебного процесса, но не его формирования. Причина этого заключается, в первую очередь, в трудностях формализации и отсутствии подходящего математического аппарата.

Одна из основных проблем адаптивного подбора заданий (как в системах адаптивного тестирования, так и обучения), опирающегося на оценки IRT (Rasch, 1980), обусловлена приблизительным равенством вероятностей правильного и неправильного выполнения заданий, что делает результаты тестирования зависимыми в основном от посторонних случайных факторов, не связанных с измеряемыми конструктами. В 2010—2012 гг. был разработан метод адаптивного тестирования (Kuravsky et al., 2012), построенный на и|)именении идентифицируемых марковских моделей с непрерывным временем и байесовской классификации.

Как развитие этого результата, в 2017 г. предложен новый вариант марковской модели адаптивного тестирования с дискретным временем (Kuravsky et al., 2017), предполагающий оценки конструктов с использованием предельных распределений вероятностей пребывания в состояниях, вычисленных с помощью матриц вероятностей переходов. В определенном смысле этот подход может рассматриваться как расширение IRT, поскольку модель Г. Раша используется в качестве его компонента.

Созданные марковские модели адаптивного тестирования стали основой при разработке адаптивного тренажера для обучения неформализуемым умениям и навыкам, необходимым для решения математических и других комплексных задач достаточно высокой сложности, требующих владения, как стандартной техникой построения рассуждений, так и элементами творческого мышления. Особенностями методов, используемых при выборе предъявляемых заданий и обеспечивающих преимущества нового подхода перед аналогами, являются:

—  выявление и использование при построении расчетных оценок временной динамики изменения способности справляться с заданиями;

—  возможность учета при построении расчетных оценок времени, затрачиваемого на выполнение заданий;

—   меньшее по сравнению с другими подходами число заданий, которые следует предъявлять, что ускоряет процесс тестирования, либо позволяет получать более надежные оценки за сопоставимое время.

Представленный подход наиболее эффективен не при начальном знакомстве с учебным материалом, а в ситуациях, когда требуется привести в систему и упорядочить уже
полученные знания, умения и навыки в единую качественно новую структуру: в частности, при подготовке к экзаменам.

Одной из особенностей второго подхода, рассмотренного в работе, является возможность решать задачи адаптивного обучения в условиях наличия ограниченного объема результатов наблюдений. В таких случаях построение надежных выводов желательно выполнять непосредственно по эмпирическим данным, минимизируя необходимые теоретические построения. В качестве решения, согласующегося с указанными требованиями, был разработан метод паттернов (Куравский и др., 2018) для диагностики испытуемых по так называемым тестовым траекториям — последовательностям значений, представляющим результаты выполнения тестовых заданий в порядке их появления. Тестовые траектории могут содержать как временные ряды данных, разбитых по субтестам, так объединенные временные ряды, собранные в общую последовательность. В отличие от созданных ранее методов рассматриваемый подход позволяет:

—   учитывать динамику результативности выполнения тестовых заданий;

—   работать с диагностическими характеристиками, непрерывно зависящими от времени (что, как правило, имеет место при диагностике операторов сложных технических систем) (Grevtsov, 2008, Krasilshchikov et al., 2011);

—   строить на своей основе адаптивные технологии тестирования, позволяющие, в зависимости от результатов конкретного испытуемого, изменять как количество предъявляемых тестовых заданий, так и их содержание, добиваясь заданного уровня надежности диагностической оценки.

Оба описанных выше подхода предназначены для адаптивного тестирования, направленного на оценку уровня способностей или сформированности навыков у испытуемого. В этой работе представлено их дальнейшее развитие, реализующее процедуры адаптивного обучения и, в частности, позволяющее:

—   обеспечивать адаптивность не только в отношении числа предъявляемых заданий, но и в отношении содержания обучающих материалов;

—   вместо бинарного представления результатов выполнения заданий (выполнено/не выполнено), учитывать суммарную трудность различных по этому показателю успешно решенных заданий как функцию времени;

—   использовать задания, связанные с несколькими шкалами измерений.

Далее в работе представлены две концепции адаптивного обучения и сравнительный анализ различных аспектов их практического применения.

Адаптивное обучение с использованием самообучающейся вероятностной модели

Процесс выбора заданий в системе производится с использованием марковских случайных процессов с дискретными состояниями и непрерывным временем. Подлежащими идентификации параметрами являются интенсивности переходов между состояниями. Динамика вероятностей пребывания в состояниях модели определяется системой обыкновенных дифференциальных уравнений Колмогорова в матричной форме:

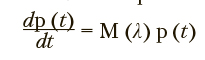
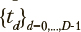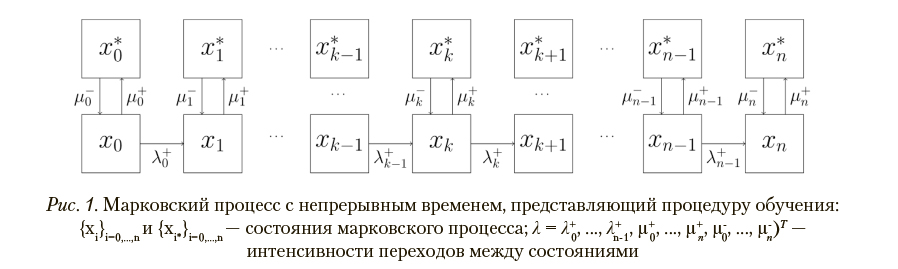
где 0 < t < T, p(t) — вероятности пребывания в состояниях процесса, Л — множество интенсивностей переходов между состояниями, M — матрица интенсивностей переходов между состояниями. Значения указанных интенсивностей определяются начальными распределениями вероятностей и наблюдаемыми частотами пребывания в состояниях F_i,d в моменты времени , где i — индексы состояний рассматриваемого марковского процесса; D — количество моментов времени, в которые фиксировались частоты 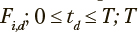 — конечный момент времени. Для описания того, как вероятности нахождения в заданных состояниях изменяются со временем, применяются процессы, организованные по схеме, изображенной на рис. 1. Эта схема представляет собой конечную цепь из 2n+2 состояний, в которой переходы из состояния  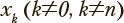возможны только в следующее по порядку состояние x_k+1 или состояние x_k*. Из состояний x₀ и x_n доступны только состояния  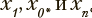соответственно. Из состояния 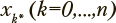доступно только состояние x_k. Для сетей указанного типа 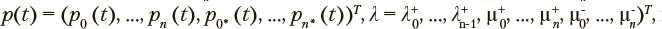матрица M имеет порядок 2n + 2.

Содержательному уровню знаний, умений и навыков, имеющему номер k, ставятся в соответствие состояния x_k и x_k*. Для каждого номера k определяется свое множество заданий соответствующего содержания. Чем правее состояние, тем шире допустимый набор знаний, умений и навыков. Состояниям с большим номером могут (но не обязаны) соответствовать задания, включающие знания, умения и навыки для состояний с меньшим номером. В общем случае полный набор знаний, умений и навыков соответствует крайнему правому состоянию.

Более высокий содержательный уровень, как правило, требует знаний, умений и навыков, соответствующих предшествующим уровням (т. е. — в указанном смысле — с повышением содержательного уровня происходит накопление знаний, умений и навыков).

Под обучаемым далее понимается человек, проходящий процедуру обучения. Полагается, что каждый обучаемый имеет один из заданных уровней подготовки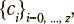, где (z+1) — число уровней подготовки, причем каждому из указанных уровней подготовки (например, высокому, среднему или низкому) ставятся в соответствие задания с определенным уровнем трудности. Каждому содержательному уровню знаний, умений и навыков соответствуют задания всех уровней трудности.

Например, могут быть использованы следующие уровни подготовки:

—   умение выполнять действия по заданному образцу (низкий уровень);

—   умение выполнять мыслительные операции, включая сравнение и анализ (средний уровень);

—   умение творчески формировать новые способы решения задач из имеющихся правил и предписаний (высокий уровень).

Каждому сочетанию содержательного уровня и уровня подготовки соответствует свой набор задач. Количество задач в каждом наборе должно быть достаточным для проведения нескольких сеансов тренажа для одного обучаемого.

В случае пребывания обучаемого в состоянии x_k, предъявляемое ему задание выбирается из множества, сопоставленного этому состоянию, случайным образом. Для каждого задания задается наибольшее допустимое время, отводимое для его выполнения.

Перемещения между состояниями определяются следующими правилами:

—  если обучаемый, находясь в состоянии x_k, правильно выполняет полученное задание, не превысив заданных ограничений по времени, он переходит в состояние x_k+1;

—  если обучаемый, находясь в состоянии x_k, неправильно выполняет полученное задание, не превысив заданных ограничений по времени, он остается в состоянии x_k;

—  если обучаемый, находясь в состоянии x_k и выполняя полученное задание, превышает заданные ограничения по времени, он переходит в состояние x_k*;

—  если обучаемый, находясь в состоянии x_k* и выполняя полученное задание, превышает заданные ограничения по времени или неправильно выполняет полученное задание, не превысив заданных ограничений по времени, он остается в состоянии x_k*;

—  если обучаемый, находясь в состоянии x_k*, правильно выполняет полученное задание, не превысив заданных ограничений по времени, он возвращается в состояние x_k.

В начальный момент времени обучаемый находится в состоянии x₀. По завершении процедуры тренажа он оказывается в одном из состояний, наилучшим образом соответствующих его уровню знаний, умений и навыков. Тренаж завершается либо при превышении общего лимита времени, отведенного на эту процедуру, либо после успешного выполнения задания в состоянии x_n без превышения лимита времени, отведенного на это задание.

При выборе заданий для обучаемых используется информация, содержащаяся в матрицах успешных переходов. Значения свободных параметров марковских сетей идентифицируются путем сравнения наблюдаемых и прогнозируемых гистограмм, описывающих распределения частот пребывания в состояниях модели, а именно: вычисляются значения, обеспечивающие наилучшее соответствие наблюдаемых и ожидаемых частот попадания в определенное состояние системы в заданные моменты времени. При этом определяется набор интенсивностей А, обеспечивающий наименьшее значение статистики Пирсона

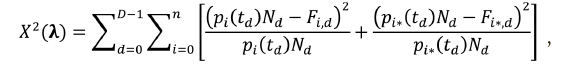
где 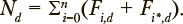 Эта статистика используется как мера соответствия модели наблюдениям. Идентификация марковских моделей с непрерывным временем проводится по выборкам обучаемых, отдельно для каждого из рассматриваемых уровней подготовки. Каждому уровню подготовки 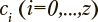при этом ставится в соответствие свой уникальный набор оценок параметров модели  λ, что позволяет в дальнейшем выявлять значение этого показателя, наилучшим образом согласующегося с наблюдениями.

Для выполнения соответствующей процедуры необходимо задать систему уравнений 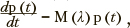, начальные условия p (0), начальное приближение λ⁰, наблюдаемые частоты 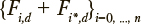пребывания в состояниях модели, шаг интегрирования λt для численного решения системы уравнений и точность оценки. Для решения задачи идентификации разработан специальный численный метод (Куравский и др., 2015, 2017). В результате решения определяется вектор λ, оставляющий минимум функционалу X²(λ).

Марковские процессы, структура которых представлена на рис. 1, идентифицируются отдельно для каждого сочетания уровня подготовки и уровня трудности. Поскольку между уровнями подготовки и уровнями трудности здесь полагается взаимно-однозначное соответствие, для z+1 уровня подготовки требуется (z+1)² идентифицированных сетей.

Трудность задания, предъявляемого обучаемому, соответствует текущей оценке его уровня подготовки. В начальный момент тренажа предъявляется задание с самым низким уровнем трудности и самым низким содержательным уровнем. После того как обучаемый, находящийся в некотором состоянии марковского процесса, завершает попытку выполнения очередного задания, вычисляются z+1 байесовских оценок вероятностей принадлежности его к рассматриваемым уровням подготовки (Kuravsky et al., 2016). При этом используются только те идентифицированные марковские процессы, которые соответствуют уровню трудности последнего предъявленного задания. Если наиболее вероятным оказывается уровень подготовки, не совпадающий с оценкой, сделанной после выполнения предыдущего задания, то обучаемому приписывается этот вновь вычисленный наиболее вероятный уровень подготовки, а сам он переводится в начальное состояние x0 (происходит «сброс состояния»). Для переходов в это начальное состояние целесообразно обеспечить некоторую «инертность», выполняя задания только в том случае, если указанная наибольшая вероятность превысит оценку вероятности текущего уровня подготовки не менее чем на заданное пороговое значение. По завершении попыток выполнения заданий самого низкого содержательного уровня «сбросы состояний» не происходят.

Таким образом, процесс тренажа сводится к предъявлению его участникам заданий, требующих для своего решения определенных знаний, умений и навыков при наличии определенного уровня подготовки. Формальная цель тренажа — привести обучающегося в крайнее правое состояние марковского процесса, что соответствует освоению всех знаний, умений и навыков при некотором уровне подготовки. В процессе тренажа используется адаптивный принцип выбора предъявляемых заданий, согласно которому их трудность должна соответствовать текущей оценке уровня подготовки обучаемых.

В процессе функционирования система дообучается на основе вновь поступающих данных о времени и успешности выполнения заданий обучаемыми. Самообучение обеспечивает:

—   решение задачи оптимизации идентифицируемых параметров (интенсивностей перехода между состояниями марковского процесса) по мере накопления результатов наблюдений за обучением тех, кто работает на тренажере;

—   решение задачи развития умений и навыков обучаемых за счет подбора заданий, способствующего их успешному выполнению, что стимулирует процесс обучения.

Для решения первой задачи после накопления достаточного объема результатов тренировок и, соответственно, расширения обучающей выборки проводится уточняющая идентификация параметров марковских процессов для всех рассматриваемых уровней подготовки.

Решение второй задачи подразумевает формирование квадратной матрицы U_i размера r х r (где r — число заданий, содержащихся в системе) успешных переходов для каждой из категорий c_i = (i = 1, ..., I). Элементы матрицы переходов являются выборочными оценками вероятностей u_mn,i успешного выполнения задания m при условии выполненного задания n обучаемым, принадлежащим категории c_i. В случае переходов с повышением содержательного уровня (из состояния xk в состояние x_k+1) обучаемому предлагаются задания, которые имеют текущую оценку вероятности успешного выполнения, превышающую 0,75 (при их наличии в системе). Задания, удовлетворяющие этому условию, выбираются случайным образом. Если подобные задания отсутствуют, то матрица успешных переходов при их выборе не используется. Подобная организация выбора заданий способствует постепенному развитию умений и навыков за счет постановки перед обучаемыми реально достижимых целей в зоне ближайшего развития.

Программная реализация данного подхода выполнена в виде интернет-системы. Эта система позволяет настраивать обучающие материалы, а именно:

—  вводить информацию о новых разделах и содержательных уровнях, представляющих собой темы, упорядочиваемые по степени сложности;

—  создавать справочные материалы по темам с описанием различных способов решения тренировочных задач, аналогичных представленным;

—  вводить задания с выбором различных алгоритмов проверки корректности ответа и указанием их трудности и допустимого времени, отведенного на решение.

В пилотной версии используются содержательные уровни, определяемые разделом дисциплины, и три уровня подготовки:

—   умение выполнять действия по заданному образцу (низкий уровень),

—  умение выполнять мыслительные операции, включая сравнение и анализ (средний уровень),

—  умение творчески формировать новые способы решения задач из имеющихся правил и предписаний (высокий уровень).

3. Адаптивное обучение на основе многомерного статистического анализа вейвлет-представлений траекторий выполнения заданий и матриц рекомендуемых переходов

Полагается, что каждый обучаемый может быть отнесен к одному и только одному из заранее заданных классов, представляющих все допустимые сочетания возможных типов субъектов, проходящих обучение, и стадий обучения, каждая из которых предназначена для одного или нескольких указанных типов. Каждому из этих классов, обозначаемых индексами i ∈ {0, ..., I}, соответствует один и только один заранее определенный сценарий обучения. Множество этих сценариев включает формальный сценарий «Завершить обучение», не содержащий заданий. Совпадение сценариев обучения для различных классов допускается. Для каждого из классов  i ∈ {0, ..., I}, определен один и только один последующий класс, которому соответствует рекомендуемый сценарий продолжения обучения. Переходы между указанными классами и, следовательно, сценариями обучения, представляются матрицами рекомендуемых переходов 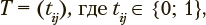 единичное значение t_ij. представляет переход из класса j в класс i, а нулевое — отсутствие такого перехода. Эти матрицы содержат динамически изменяемую эмпирическую информацию, обобщающую накопленный опыт. Процедура адаптивного обучения начинается со сценария, соответствующего так называемому начальному классу i₀. В каждый момент обучения реализуется сценарий, соответствующий некоторому текущему классу  i ∈ {0, ..., I}.

Фрагменты деятельности обучаемых с известными диагностическими показателями представлены результатами выполнения ими последовательностей заданий, соответствующих указанным сценариям обучения. Эти результаты вместе с информацией о классах обучаемых хранятся в соответствующей базе данных, образуя контрольные выборки для каждого из рассматриваемых классов.

Алгоритмические аспекты процесса адаптивного обучения, основанного на анализе вейвлет-представлений траекторий выполнения заданий (Laxhammar, Falkman, 2014) и матриц рекомендуемых переходов, представлены ниже.

Шаг 0. Определение начального сценария обучения. Первым по порядку реализуется сценарий обучения, соответствующий начальному классу i0, который на данном шаге рассматривается как текущий класс.

Шаг 1. Сбор данных. Обучаемому предъявляется или определенная индексом текущего класса последовательность заранее подготовленных заданий для каждой рассматриваемой характеристики (при этом считается, что задание связано только с одной измеряемой велт-итиной), или соответствующая текущему классу последовательность универсальных многомерных заданий, с каждым из которых связано сра.'зу i[('сколько измеряемых характеристик. Сфо рр| н р>о на и ыая в процессе выполнения предъявленных заданий последовательность результатов заносится в базу данных и подвергается анализу на последующих шагах. 11ри этом она иреобр^уется так, что каждый элемент запоминаемого временного ряда представляет собой кумулятивную сумму измеренных в логитах (Rasch, 1980) трудностей успешно выполненных заданий (от начала последовательности до текущего задания). Нулевые значения шкалы трудностей устанавливаются так, чтобы соответствовать минимальному уровню этой величинывлогитах.

Шаг 2. Удаление избыточной информации. Избыточная информация, содержащаяся в представленных выше временных рядах, удаляется с помощью метода главных компонентов (Vidal, 2016; Kong, 2017). Для этого вычисляются матрицы взаимных корреляций исследуемых временных рядов, решается алгебраическая проблема собственных значений и выясняется, насколько можно понизить размерность собственного подпространства главных компонентов с условием сохранения достаточно высокой доли (на практике, от 70% и выше) суммарной изменчивости наблюдений, представленной соответствующей дисперсией. Для каждого из оставшихся собственных направлений по одной из наибольших компонентных нагрузок выбирается представитель из числа субтестов или регистрируемых параметров (прямой переход к базису главных компонентов нецелесообразен из-за их неопределенной интерпретации). Цель этого — сохранить для последующего анализа только относительно независимые характеристики, заменяя группы существенно зависимых показателей одним представителем.

Шаг 3. Переход к интегральным характеристикам временных интервалов, используя дискретное вейвлет-преобразование. Временные ряды, представляющие процесс обучения, заменяются наборами вейвлет-коэффициентов, полученных в результате кратномас­штабного анализа (Neal, 2010). При этом исходные исследуемые процессы как функции времени заменяются интегральными характеристиками, привязанными к временным интервалам в области их определения (Srivastava A., Feron E., 2011) Кратномасштабный анализ позволяет существенно сократить число показателей, необходимых для корректного представления процессов, поскольку число вейвлет-коэффициентов, используемых на последующих этапах, может быть существенно меньше, чем длина соответствующих исходных временных рядов.

Шаг 4. Вычисление матриц взаимных расстояний. Для каждой предметной области вычисляется матрица взаимных расстояний между полученными на шаге 3 вейвлет- представлениями процессов выполнения заданий каждым обучаемым. При этом матрицы взаимных расстояний для различных параметров, участвующих в анализе, складываются,
формируя итоговую матрицу. Размерность таких матриц равна объему выборки обучаемых, подлежащих анализу. Предполагается, что информация о результатах выполнения заданных контрольных последовательностей заданий (сценариев обучения) для каждого обучаемого хранится в соответствующей базе данных.

Шаг 5. Многомерное шкалирование для анализа взаимного расположения обучаемых в пространстве приемлемой размерности. Вычисленное взаимное расположение обучаемых в пространстве многомерного шкалирования (Trevor, Cox, 2001; Borg, Groenen, 2011) является основой для диагностических решений. Размерность пространства шкалирования определяется, исходя из условия достаточной дифференциации предусмотренных категорий обучаемых.

Шаг 6. Кластеризация обучаемых в пространстве шкалирования. Координаты расположения обучаемых в пространстве, полученном в результате многомерного шкалирования, являются входными данными для процедуры кластеризации (Gariel et al, 1999; Gaffn\v, Smyth, 1999, 2001; Li et al., 2010; Enriquez, Kurcz, 2012; Hung et al.. 2015; Wilson et al.. 2016; Eerland, Box, 2016). Цель — выявить субъектов, наиболее близких по результатам обучения.

Шаг 7. Вычисление расстояний до центров кластеров обучаемых или до ближайшего фрагмента деятельности по результатам выполнения последовательности заданий. В случае достаточно больших выборок, вычисляется расстояние до центров определенных на шаге 5 кластеров обучаемых в пространстве шкалирования. Если выборки малы, то определяется ближайший фрагмент деятельности из базы данных, что может быть выполнено двумя способами: либо непосредственно, вычисляя ближайший фрагмент деятельности в евклидовой метрике вейвлет-представлений, либо путем выявления такого фрагмента в итоговом пространстве шкалирования, используя ту же метрику.

Шаг 8. Распознавание классов обучаемых с помощью выборочных функций распределений расстояний до центров кластеров. Вероятностные оценки принадлежности обучающихся определяются с помощью выборочных функций распределений F_i(X) евклидовых расстояний X о центров кластеров, соответствующих распознаваемому классу  i ∈ {0, ..., I} в результирующем пространстве шкалирования. Вычисленные величины 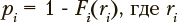 — евклидово расстояние до центра i-го кластера, рассматриваются как оценки вероятности принадлежности рассматриваемого обучающегося к заданным классам. Распределение по классам 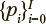характеризует надежность полученной оценки. Данный подход фактически реализует в обобщенной форме идею линейного дискриминантного анализа, не требуя при этом наложения ряда ограничений на результаты наблюдений.

Шаг 9. Выбор текущего класса обучаемого или ближайших представителей разных классов с оценкой различий по конкретным параметрам. В В случае достаточно больших выборок, в пространстве шкалирования определяется класс индексом i_max вероятность р_i gринадлежности к которому, вычисленная на предыдущем шаге, является наибольшей. Если такой класс не является единственным или выборки малы, то определяется ближайший фрагмент деятельности с индексом i_c из базы данных, что может быть выполнено либо непосредственно, вычисляя ближайший фрагмент деятельности в евклидовой метрике вейвлет-представлений, либо путем выявления такого фрагмента в итоговом пространстве шкалирования, используя ту же метрику. Выявленный класс с индексом i_max или i_c рассматривается далее как текущий.

Шаг 10. Определение нового текущего класса. Для текущего класса с помощью матрицы рекомендуемых переходов T пределяется последующий класс. Выявленный последующий класс далее полагается текущим. Если новому текущему классу соответствует формальный сценарий «Завершить обучение», то выполняется переход на шаг 11, иначе — переход на шаг 1.

Шаг 11. Останов.

Таким образом, адаптивность представленного подхода достигается за счет n^c^(^<^j^a оптимальных сценариев обучения с опорой на анализ динамики выполнения ywtmbw: заданий. Для этооо используются методы многомерного статистического анализа вейвлет-представлений траекторий выполнения заданий и информация, содержащаяся в матрицах рекомендуемых переходов. Для практических приложений важно, что рассмотренный подход применим при наличии в базе данных как достаточно больших, так и малых выборок фрагшнтовдеятелъностиобучсизмых.

Описания методов многомерного статистического анализа вейвлет-представлений траекторий выполнения заданий и их различные практические применения представлены в работах Л.С. Куравского с соавт. (Куравский и др., 2018; Kuravsky et al., 2019). Эти методы программно реализованы в Intelligent System for Flight Analysis (ISFA) с использованием системы графического программирования LabVIEW.

Сравнительный анализ представленных концепций адаптивного обучения

Общие комментарии

Подход, основанный на многомерном статистическом анализе вейвлет-представлений траекторий выполнения заданий, предполагает подбор оптимального сценария обучения на основе анализа динамики выполнения заданий и сопутствующей статистической информации. С точки зрения процесса обучения, подбор оптимального сценария обучения может быть более эффективным, чем подход с использованием самообучающегося марковского процесса, предполагающего наличие большого числа заданий для каждого содержательного уровня. Каждое задание, помимо характеристики принадлежности к содержательному уровню, обладает показателем трудности и ограничения на время выполнения. В качестве предварительного показателя временного ограничения можно использовать экспертную оценку, а после накопления необходимого для функционирования системы объема выборки — некоторую усредненную величину. Предполагается, что трудность заданий и их соответствие содержательным уровням определяется с помощью эксперта. Во втором подходе задача оценки ограничений времени выполнения для каждого задания не решается явно — предполагается, что наличие известных сценариев обучения корректно представляет временную динамику выполнения заданий для различных классов испытуемых.

Одной из важных задач, решаемых в процессе функционирования систем, основанных на втором подходе, является задача определения размерности пространства шкалирования для последующего достижения заранее установленного качества дифференциации обучаемых. Решение данной задачи зависит от начального объема хранимых сценариев обучения в базе, от результатов применения метода главных компонентов и от параметров вейвлет-преобразо- вания. Большой объем хранимых фрагментов деятельности обучаемых может сократить размерность результирующего пространства, упростив интерпретацию результатов кластерного анализа. Подход, основанный на использовании самообучающегося марковского процесса, в меньшей степени зависит от параметров промежуточных процедур. Оценка принадлежности испытуемого производится с помощью вычисления условных вероятностей по окончании времени обучения и пребывания испытуемого в фиксированном состоянии модели.

Системы обучения (в том числе адаптивные) предполагают повторение процедур обучения до достижения целевого уровня навыков. При этом базы данных систем должны располагать большим количеством различных заданий с определенными характеристиками, соответствующими различным уровням трудностей и содержательным уровням. Для
относительно простых содержательных уровней такая проблема может быть решена применением специальных алгоритмов генерации заданий, однако для более сложных уровней решение задачи может быть затруднительным. Кроме задачи генерации заданий для сложных содержательных уровней, для данного этапа характерна проблема автоматической проверки ответа в случае открытого характера заданий.

Оба подхода допускают автоматическое дообучение реализующей их системы по мере накопления эмпирических данных.

Первый подход позволяет обеспечить большую степень сокращения количества заданий, необходимых для предъявления испытуемым.

Необходимый объем эмпирических данных

В обоих подходах используются эмпирические данные. Идентификация моделей в случае первого подхода производится на основе эмпирических частот пребывания в состояниях модели, что может потребовать достаточно объемных выборок. Малые объемы выборок могут привести к неустойчивым оценкам значений свободных параметров и матриц успешных переходов. В то же время особенностью подхода на основе самообучающейся марковской модели является постоянное обновление и корректировка оценок компонентов этой матрицы.

Во втором подходе так же, как и в первом, используются заранее собранные эмпирические данные, однако его реализация допускает предельно малые выборки: на шаге 7 в качестве ближайшего объекта будет рассматриваться не центр кластера (случай большой выборки), а ближайший фрагмент деятельности, содержащийся в базе данных. Этот подход позволяет накапливать результаты наблюдений и, после появления в базе достаточного числа похожих фрагментов деятельности, объединить их в кластер.

Таким образом, второй подход допускает работу с меньшими объемами эмпирических данных, чем первый.

Программная реализация

Сложность программной реализации двух представленных подходов обусловлена выбором языка реализации. Учитывая нетривиальную математическую составляющую как первого, так и второго подходов, для реализации следует выбирать программные среды, дающие доступ к надежным средствам вейвлет-преобразований, численной оптимизации, решения систем дифференциальных уравнений и т. д.

Современные технологии адаптивного тестирования все чаще реализуются в виде ин- тернет-ресурсов — это позволяет эффективно накапливать и обрабатывать данные испытаний. Кроме того, веб-реализации позволяют существенно расширить круг испытуемых за счет возможности дистанционного прохождения тестов. Это справедливо и для систем адаптивного 015- учения: большой объем выборки позволяет накапливать информацию, необходимую для формирования и корректировки траекторий обучения конкретного испытуемого. Реализация приведенных в работе подходов к адаптивному ovowionnio может быть выполнена стандартными средствами веб-разработки, однако для наиболее сложных этапов обеих технологий рекомендуется либо использовать специализированные среды (LabVIEW, MATLAB, R, Julia, Python — с обязательным использованием пакета numpy), либо создавать соответствующие модули на языке C++.

Достаточно трудной частью реализации подхода, основанного на использовании самообучающихся марковских процессов, является идентификация моделей для каждого уровня подготовки. В общем случае этот процесс может занимать продолжительное в|)омя. Для роиio-
ния подобных задач был разработан метод дискретизации значимых параметров (Kuravsky et al., 2015; Куравский и др., 2017), существенно снижающий размерность пространства параметров, значения которых определяются в процессе решения задачи идентификации.

Учитывая необходимость идентификации систем дифференциальных уравнений, описывающих вероятностную динамику пребывания в состояниях марковских процессов, первый подход представляется более сложным, как в вычислительном плане, так и для программной реализации.

        Финансирование

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 17-29-07034).