Управляющие функции в процессе формирования эффекта серии: торможение, обновление и переключение

Данная работа направлена на изучение возможных механизмов формирования эффекта серии. Ранее было показано, что управляющие функции являются системообразующим элементом в структуре механизмов формирования и разрушения эффекта серии. В приведенном исследовании в качестве возможных механизмов рассматриваются отдельные управляющие функции (переключение, обновление, торможение), загрузка которых должна повлиять на формирование эффекта. Для моделирования эффекта серии используются адаптированные задачи Лачинсов двух типов – арифметические и вербальные. Загрузка отдельных управляющих функций осуществляется в рамках парадигмы вторичной задачи. Продемонстрировано, что параллельная загрузка управляющих функций любого типа не мешает формироваться эффекту серии на материале арифметических задач. При этом загрузка функции переключения негативно влияет на формирование эффекта серии на материале вербальных задач. Таким образом, параллельная загрузка управляющих функций может, с одной стороны, приводить к ослаблению фиксации, с другой, к усилению. В частности, низкая загрузка управляющих функций ведет к формированию эффекта серии, увеличение загрузки приводит к ослаблению фиксации, перегрузка влечет за собой увеличение фиксации. Таким образом, общий уровень загрузки управляющих функции играет ключевую роль в процессе формирования эффекта серии, а взаимодействие между ними можно описать как U-образную кривую.

Введение

Проблема изучения механизмов эффекта серии

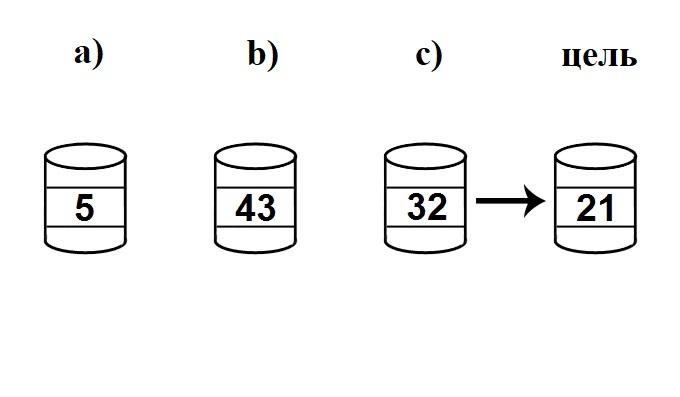
Изучение эффекта серии имеет довольно долгую историю, однако до сих пор нет согласованных представлений о механизмах данного феномена. Эффект серии (mental set, Einstellung effect) – это тенденция решать задачи определенным образом, опираясь на опыт решения схожих проблем. Вопреки расхожему мнению о том, что впервые эксперименты с серийной организацией мыслительных задач были представлены в диссертационной работе А. Лачинса [Luchins, 1942], он сам ссылался на неопубликованные эксперименты К. Зенера и К. Дункера 1927 года, а одной из первых опубликованных работ стала статья Х. Рис и Х. Исраила [Rees, 1935], в которой эффект серии моделировался на материале анаграмм. Методологические основы изучения эффекта серии были заложены еще в работах последователей Вюрцбургской школы, в частности, в работах Н. Аха и О. Кюльпе [Асмолов, 2002; Ach, 1910], однако именно работа А. Лачинса стала хрестоматийной. А. Лачинс разработал три типа задач: задачи на переливание, пространственные лабиринты и вербальные задачи [Luchins, 1942]. Наиболее масштабную экспериментальную разработку получили исследования с задачами на переливание. Испытуемым необходимо было, используя три кувшина заданной емкости, путем переливания из одного в другой отмерить определенное количество воды (см. рис. 1).

Рис. 1. Установочная задача Лачинсов.

Инструкция: «Перед Вами три кувшина емкостью 5 л, 43 л, 32 л. Задача, используя данные кувшины для переливания из одного в другой, отмерить 21 л».

Ответ: 43 – 32 + 5 + 5=21

Для формирования установки в работах Лачинсов [Luchins, 1942; Luchins, 1950] серия задач была организована следующим образом:

• первая задача тренировочная;
• со второй по шестую задачи решаются в три действия по одной схеме (например, как на рис. 1, схема решения: b – c + 2a);
• седьмая и восьмая задачи критические и решаются двумя способами:  установочным или более длинным, например, b – c + 2a, а также более коротким способом, например, c – a;
• девятая задача – критическая (extinction problem), она решается только одним оптимальным коротким способом, например, c – a;
• десятая и одиннадцатая задачи снова решаются двумя способами: установочным и более коротким.

Было продемонстрировано, что серия из пяти установочных задач провоцирует почти 80% испытуемых решать задачи, включающие два решения, установочным способом. Более того, испытуемые после решения испытывали значительные трудности при решении критической девятой задачи, которая решается в одно действие, и были склонны возвращаться к установочному способу решения в десятой и одиннадцатой задачах.

Демонстрация феномена повлекла за собой ряд экспериментальных исследований, в которых эффект воспроизводился на различном материале, а путем манипуляций с условиями, авторы данных работ пытались воздействовать на усиление или ослабление фиксации. В частности, было продемонстрировано, что усиление фиксации вызывают увеличение количества установочных задач [Crooks, 2009; Luchins, 1942], однако в работе М. Тресселта и Д. Лидса [Tresselt, а] не было показано влияния данного фактора на формирование эффекта серии; ограничение времени, отведенное на решение [Luchins, 1942]; сложность установочной схемы решения [Knight, 1963]; высокий уровень тревожности или стресса [Cowen, 1952; Luchins, 1942; Maltzman, 1953]; усвоенная ранее схема решения задачи на другом материале [Jacobus, 1964]; хаотичные изменения иррелевантных параметров задач [Тухтиева, 2013] и мн. др. В свою очередь, ослабление фиксации провоцируют включение в установочную серию задач, которые решаются различными способами [Luchins, 1942]; введение временных интервалов между решением установочных задач [Kendler, 1952]; подсказки по типу «Не будь слеп!» [Luchins, 1942]; перетренированность на установочном способе решения [Juola, 1967; Juola, 1968]; регулярные изменения иррелевантных параметров задач [Тухтиева, 2013] и мн. др. Не было обнаружено влияния на формирование эффекта серии таких условий, как смена позиций кувшинов [Aftanas, 1962]; введение промежутка времени после решения установочных задач [Luchins, 1942]; ограничение количества жидкости для задач на переливание, которое можно использовать [Luchins, 1950]; использование настоящих банок и воды при решении задач на переливание [Luchins, 1950; Tresselt], однако в более современной работе Ф. Валле-Туранжо и коллег [Vallée-Tourangeau, 2011] было продемонстрировано, что интерактивность все же приводила к ослаблению фиксации.

Как справедливо отмечает Дж. Дженсен [Jensen, 1960], ахиллесовой пятой данных экспериментальных результатов являлось отсутствие четких представлений о механизмах формирования эффекта. Во многом трудности, относящиеся к разработке теоретической концепции механизмов феномена, могли быть связаны с тем, что эффект серии включает в себя два независимых процесса – формирование схемы и ее преодоление. Еще Х. Гутцков писал о том, что восприимчивость к формированию установки и способность к её преодолению являются двумя независимыми способностями [Guetzkow, 1951]. Таким образом, разрабатывая проблему механизмов эффекта серии, необходимо обращаться и возвращаться к данному положению, поскольку одни механизмы могут быть задействованы на этапе формирования схемы решения, а другие – на этапе разрушения старой схемы и формирования новой.

Механизмы эффекта серии: управляющие функции

Наиболее перспективным претендентом для рассмотрения в качестве механизма формирования и разрушения эффекта серии является конструкт рабочей памяти (РП) [Владимиров, 2018; Beilock, 2007; Van Stockum Jr, 2020]. РП — это система временного хранения информации, задействованная при решении широкого класса когнитивных задач [Величковский, 2017; Козлов, 2019; Савинова, 2023; Baddeley, 2002; Baddeley, 1974; Cowan, 1999; Oberauer, 2019]. Формируясь в экспериментальных условиях, эффект серии, по всей видимости, напрямую связан с процессами, протекающими в РП, поскольку РП играет ключевую роль во временном хранении и обработке информации, а также обеспечивает удержание репрезентаций задачи в фокусе внимания [Величковский, 2017; Baddeley, 2002; Baddeley, 1974; Cowan, 1999; Oberauer, 2019]. Конструкт РП связывают с такими функциями как запоминание, кодирование и извлечение из долговременной памяти, регуляция внимания и обработка информации. Согласно теории А. Беддели, РП включает в себя ряд блоков: фонологическую петлю, зрительно-пространственный блокнот, эпизодический буфер и центральный исполнитель [Baddeley, 2002; Baddeley, 1974]. Первые три блока относятся к пассивной системе модально-специфических хранилищ и мультимодального эпизодического буфера, в свою очередь, центральный исполнитель является контролирующей активной системой внимания [Korovkin, 2023], к функциям которого относятся управление работой модально-специфических блоков РП и функции внимания. Ранее было продемонстрировано [Владимиров, 2018], что при формировании эффекта серии именно контролирующая система внимания, а не модально-специфические хранилища играют ключевую роль в возникновении фиксированной схемы решения задачи. В исследовании И.Ю. Владимирова и коллег [Владимиров, 2018] эффект серии формировался на материале арифметических задач Лачинсов, в процессе их решения испытуемым необходимо было выполнять вторичную задачу, которая дополнительно загружала РП. Наиболее разрушающее воздействие на формирование эффекта серии оказывала сложная материал-неспецифическая для основной задачи вторичная задача. Таким образом, именно факторы сложности и переключения с одного материала на другой оказались ключевыми для формирования устойчивой схемы решения.

Довольно долгое время центральному исполнителю отводилась роль своеобразного «гомункула» РП. В этом отношении теоретический и методический интерес, в частности, для изучения эффекта серии, представляют работы, в которых предприняты попытки дифференцировать и экспериментально продемонстрировать существование различных управляющих функций (УФ). Мы предполагаем, что разные УФ задействованы на разных этапах формирования эффекта серии. В исследовательской практике конструкт УФ тесно связан с конструктом РП, в частности, предполагается, что центральный исполнитель рабочей памяти является источником УФ [Baddeley, 2017; Baddeley, 2002; Korovkin, 2018]. А. Мияке с коллегами [Miyake, 2000] выделяют три УФ: 1) переключение (Shifting) — способность переключаться между задачами, операциями, установками; 2) обновление (Updating) — мониторинг и кодирование входящей информации, замена неактуальной информации на релевантную в РП; 3) торможение (Inhibition) — подавление доминантных, автоматических реакций. С помощью факторного анализа было продемонстрировано, что вышеописанные УФ связаны друг с другом, но четко разделены. При этом авторы говорят о том, что приведенный список функций неисчерпывающий. Стоит отметить, что в более поздних работах А. Беддели [Baddeley, 2017] приводит схожий набор функций, которые он относит к блоку центрального исполнителя: распределение и переключение внимания, подавление и избирательное реагирование, удержание и оперирование информацией из долговременной памяти.

В рамках дифференциально-психологического подхода были проведены исследования роли отдельных компонентов РП в процессе формирования и разрушения эффекта серии на материале арифметических задач Лачинсов [Beilock, 2007; Van Stockum Jr, 2020]. Для нашей работы наибольший интерес представляет статья Ч. Ван Стокума и М. ДеКаро [Van Stockum Jr, 2020]. Авторов интересовало, каким образом способность к когнитивной гибкости, под которой они понимают способность решать критические задачи не установочным, оптимальным способом, связана с успешностью выполнения проб на РП. Использовались три типа задач, которые были связаны со следующими конструктами:

• антисаккадная задача (antisaccade task) с контролем внимания, который ответственен за сосредоточение;
• спэн-тест 1 (running span task) с первичной памятью, то есть работой с информацией, которая находится непосредственно в фокусе внимания;
• спэн-тест 2 (operation span task) со вторичной памятью, то есть доступом к информации из долговременного хранилища.

Было продемонстрировано, что решение критических задач серии оптимальным способом связано с успешным выполнением спэн-теста 1 в сочетании с высокой успешностью в антисаккадной задаче; либо же с низкой успешностью по спэн-тесту 2 в сочетании высокой успешностью в антисаккадной задаче. По мнению авторов, РП одновременно отвечает за процессы ограничения и поддержания когнитивной гибкости. Для успешного переключения с неоптимальной стратегии решения, выработанной в ходе установки, важен высокий уровень когнитивного контроля в сочетании с высоким уровнем первичной памяти, либо же с низким уровнем вторичной памяти. Если подойти к анализу данного исследования с позиции работы А. Мияке и коллег, то используемые Ч. Ван Стокумом и М. ДеКаро [Van Stockum Jr, 2020] задачи загружают отдельные УФ, в частности, антисаккадная задача является задачей для загрузки торможения, а различные вариации спэн-тестов преимущественно загружают обновление. Таким образом, способность оттормозить автоматический ответ и решить критическую задачу оптимальным способом обусловлена активностью функции торможения, однако роль функции обновления в данном процессе амбивалентна.

Вполне возможно, что на разных этапах формирования эффекта серии различные виды УФ играют свою специфическую роль. Так, торможение может быть ключевым процессом, отвечающим за оттормаживание установочного шаблона решения [Van Stockum Jr, 2020], а обновление и переключение в большей степени задействованы в процессе формирования данного шаблона. Напомним, что ранее было продемонстрировано, что переключение с одного материала на другой в большей степени мешает формироваться эффекту серии [Владимиров, 2018]. В свою очередь, обновление, которое ответственно за мониторинг поступающей информации и ее кодировку в РП, также может нести основополагающую роль в процессе формирования устойчивой схемы решения задачи. Таким образом, целью данной работы является изучение роли отдельных УФ (переключения, торможения, обновления) в процессе формирования эффекта серии. Для воздействия на данный процесс в нашей работе используется метод вторичной параллельной загрузки/задачи [Baddeley, 1974; Kahneman, 1973; Reber, 1997]. Мы предполагаем, что выполнение вторичной задачи на обновление и переключение будет иметь разрушающее воздействие на эффект серии, так как на данном этапе процесс формирования устойчивой схемы решения наиболее требователен именно к данным УФ.

Процедура и методика исследования

Основная гипотеза: ключевую роль в процессе формирования эффекта серии играют переключение и обновление; торможение преимущественно задействовано в процессе оттормаживания уже сформированной схемы решения.

Частные гипотезы:

• параллельная загрузка управляющих функций, ответственных за обновление информации и переключение, будет мешать формированию эффекта серии;
• параллельная загрузка управляющих функций, ответственных за торможение импульсивных реакций, будет в меньшей степени мешать формированию эффекта серии.

Переменные экспериментального исследования:

Независимые переменные:

1. тип основных задач:

• арифметические адаптированные задачи Лачинсов;
• вербальные адаптированные задачи Лачинсов.

2. тип параллельной загрузки:

• загрузка функции переключения (локально-глобальная задача);
• загрузка функции обновления (n-back);
• загрузка функции торможения (пространственный вариант теста Струпа).

В качестве зависимых переменных выступало время решения задач серии.

Выборка экспериментального исследования

Итоговая выборка составила 59 испытуемых в возрасте от 16 до 65 лет (M = 26,3; Med = 25; σ = 8,6), 12 мужчин и 47 женщин.

Стимульный материал

Серия, формирующая установку, как для арифметических, так и для вербальных задач отличалась от классического варианта, используемого А. Лачинсом [Luchins, 1942]. Для формирования эффекта серии испытуемым необходимо было решить восемь однотипных задач, девятая задача – критическая, решалась отличным от установочного способом. Эффект серии формировался на материале адаптированных арифметических и вербальных задач Лачинсов [Luchins, 1942]. Для загрузки УФ использовались вторичные задания, которые загружали ту или иную УФ [Лазарева, 2022; Miyake, 2000; Savinova, 2023].

Серия на материале арифметических задач

Первые восемь установочных задач решались в три действия: средний кувшин минус крайний правый, два раза добавить крайний левый (b – c + a + a, см. рис. 1); девятая задача решалась в одно действие: крайний правый кувшин минус крайний левый (с – a). Стимульный материал был предварительно протестирован [Владимиров, 2018]: 1) критическая задача в установочных условиях решается значимо дольше, чем та же задача в условиях без установки; 2) критическая задача в условиях установки решается значимо дольше по времени, чем последняя установочная задача серии; 3) схема решения в условиях без параллельной загрузки усваивается постепенно, наблюдается научение.

Серия на материале вербальных задач

Перед испытуемым была представлена строчка из восьми букв, необходимо было среди них найти слово из четырех букв, в единственном числе, именительном падеже (кто? что?), нарицательное. Слово необходимо было искать слева направо, буквы местами менять не нужно, просто отметать лишние буквы-дистракторы. Буквы-дистракторы не допускали образования альтернативных слов, соответствующих условиям задачи. Последовательность из восьми букв во всех задачах была следующая: согласная-согласная-гласная-гласная-согласная-согласная-гласная-гласная (см. рис. 2). Каждая из восьми букв располагалась на цветном фоне, чтобы избежать «эффекта превосходства слова» [Фаликман, 2010].

Рис. 2. Установочная задача вербальной серии (ответ: рыба)

Специфика серии с вербальными задачами заключалась в том, что схема решения для всех восьми установочных задач была одна и та же: слово всегда начиналось со второй буквы, далее необходимо было искать через букву (см. рис. 2). В критической девятой задаче слово было написано целиком без включения дистракторов, но необходимо было начать искать ответ с пятой буквы (например, МРЮЕСТАЯ). Стимульный материал был предварительно протестирован [Лазарева, 2023]. В отличие от арифметических задач, в вербальных задачах схема решения в условиях без параллельной загрузки схватывается сразу, динамики в решении установочных задач серии не наблюдается.

Задания для параллельной загрузки УФ

При выборе заданий, параллельно загружающих отдельные УФ, мы опирались на работу А. Мияке с коллегами [Miyake, 2000], которые показали, какие из типов заданий преимущественно связаны с той или иной УФ. Так, для загрузки переключения нами использовалась адаптированная локально-глобальная задача (local-global task) — см. рис. 3:

Рис. 3. Локально-глобальная задача [Savinova, 2023]

для загрузки обновления — адаптированная задача N-шагов назад (N-back task) – см. рис. 4:

Рис. 4. Задача N-шагов назад [Savinova, 2023]

Данные задания включали работу с неспецифическим для основной задачи Лачинсов материалом (работу с фигурами), то есть требовали переключения с одного материала на другой. Трудность возникла при подборе задания на торможение. Дело в том, что наиболее распространенной задачей, используемой для загрузки торможения, является семантический вариант теста Струпа (Stroop test). Однако под цели данного исследования он не подходил в связи с выявленной в предварительных сериях спецификой работы с материал-специфической и материал-неспецифической параллельной загрузкой. Так, классический семантический вариант теста Струпа являлся бы материал-неспецифическим заданием для арифметических задач Лачинсов и материал-специфической для вербальных задач Лачинсов. В связи с этим нами был разработан пространственный вариант теста Струпа [Лазарева, 2022] — см. рис. 5. Пространственный тест Струпа являлся материал-неспецифической загрузкой как для арифметических, так и для вербальных задач. В данном задании необходимо было оттормаживать автоматические реакции и не реагировать на направление стрелки на экране компьютера при нажатии стрелки на клавиатуре.

Рис. 5. Пространственный вариант теста Струпа [Лазарева, 2022]

Процедура исследования

Каждый испытуемый решал две серии задач (вербальную и арифметическую) в условиях различной параллельной загрузки. Процедура исследования в двух сериях была одинаковая. Каждому испытуемому предлагалось решить восемь установочных задач, далее критическую задачу. Задачи решались испытуемыми устно, предъявлялись на экране компьютера, ответ испытуемому необходимо было озвучить экспериментатору. Испытуемые решали каждую задачу до нахождения верного решения, после чего могли перейти к следующей задаче.

Как во время решения установочных, так и во время решения критической задачи, испытуемые должны были выполнять параллельную задачу. Параллельная (вторичная) задача появлялась на экране внизу, под основной задачей, картинки вторичной задачи постоянно менялись, для их решения необходимо было нажимать стрелки на клавиатуре (влево или вправо). Перед каждой серией осуществлялась тренировочная серия на решение основной и параллельных задач.

Каждый испытуемый решал серию на материале вербальных и арифметических задач. Использовалось три варианта параллельных-вторичных задач: загрузка торможения, переключения и обновления. Испытуемые случайным образом были распределены в одну из 6 групп. Экспериментальный план выглядел следующим образом (см. табл. 1):

Таблица 1. Экспериментальный план исследования

Аппаратное обеспечение

Дизайн исследования создан с помощью программы PsychoPy2 v. 1.81.02, исследование проводилось на переносном персональном компьютере (HP Pavilion Laptop 14), обработка результатов исследования проводилась с помощью программы JASP.

Статистический аппарат исследования

Математическая обработка результатов проводилась с использованием следующих статистических критериев: ANOVA, ANOVA с повторными измерениями, T-критерий Стьюдента.

Результаты

Специфика формирования серии на различном стимульном материале и сложность арифметических и вербальных задач значимо различаются. Динамика формирования серии значимо различается для разного стимульного материала в условиях торможения (F (8; 296) = 2,27, p = 0,022, η2p = 0,058), переключения (F (8; 296) = 4,049, p < 0,001, η2p = 0,099) и обновления (F (8; 296) = 3,505, p < 0,001, η2p = 0,087). Среднее время первой установочной вербальной задачи (M  = 39,499, SD = 37,279) значимо меньше, чем среднее время решения первой арифметической задачи (M = 111,805, SD = 76,676), t(57) = –6,673, p < 0,001, Cohen's d = –0,876. В связи с этим, результаты будут рассматриваться отдельно для каждого типа задач (арифметического и вербального).

Влияние загрузки УФ на процесс формирования эффекта серии на материале арифметических задач Лачинсов

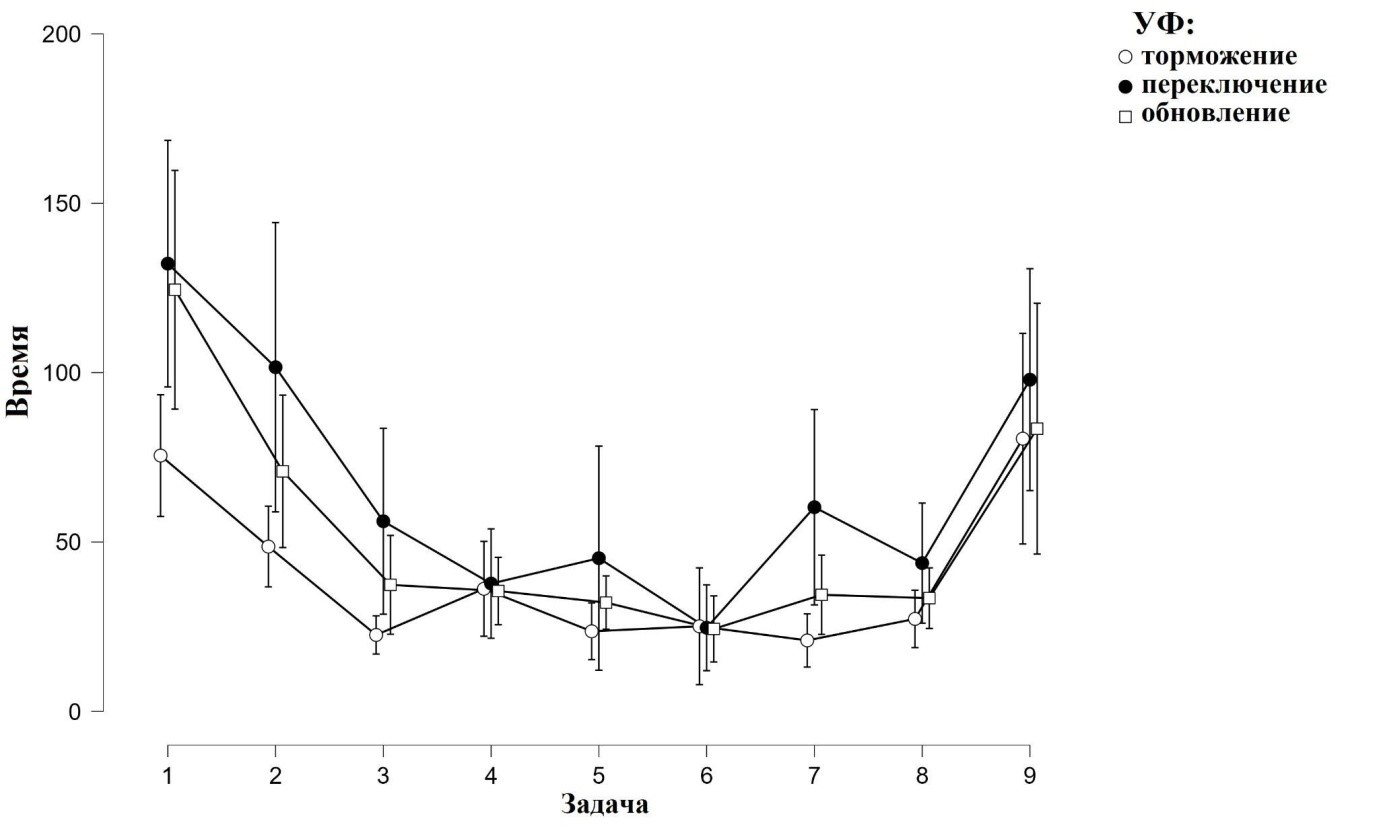
Отсутствует взаимодействие факторов тип загрузки и тип задачи, значимых различий в динамике формирования серии в условиях разной параллельной загрузки УФ не выявлено, F (16; 440) = 1,07, p = 0,389, η2p = 0,037 (см. рис. 6).

Рис. 6. Время решения (в секундах) задач арифметической серии в условиях различной параллельной загрузки УФ

При анализе времени решения установочных задач серии (с 1 по 8) были выявлены значимые различия для всех условий (переключение: F (7; 126) = 7,048, p < 0,001, η2p = 0,281; обновление: F (7; 140) = 16,962, p < 0,001, η2p = 0,459; торможение: F (7; 119) = 11,513, p < 0,001, η2p = 0,404). Таким образом, время решения установочных задач серии в ходе научения изменяется во всех трех условиях (см. рис. 6).

В пользу того, что научение происходит во всех трех условиях для арифметических задач, говорят нам значимые различия между временем решения 1 и 8 задач. Время решения 1 установочной задачи значимо больше, чем время решения 8 установочной задачи во всех условиях (см. табл. 2).

Таблица 2. Анализ различий между временем решения первой и последней установочными задачами в условиях различной параллельной загрузки УФ.

Арифметическая серия

Также значимые различия сохранялись между временем решения последней установочной (восьмой) и критической (девятой) задачами во всех условиях (см. табл. 3), то есть, вопреки выдвинутой гипотезе, все типы загрузки не помешали формированию эффекта серии.

Таблица 3. Анализ различий между временем решения последней установочной (восьмой) и критической (девятой) задачами в условиях различной параллельной загрузки УФ. Арифметическая серия

Влияние загрузки УФ на процесс формирования эффекта серии на материале вербальных задач Лачинсов

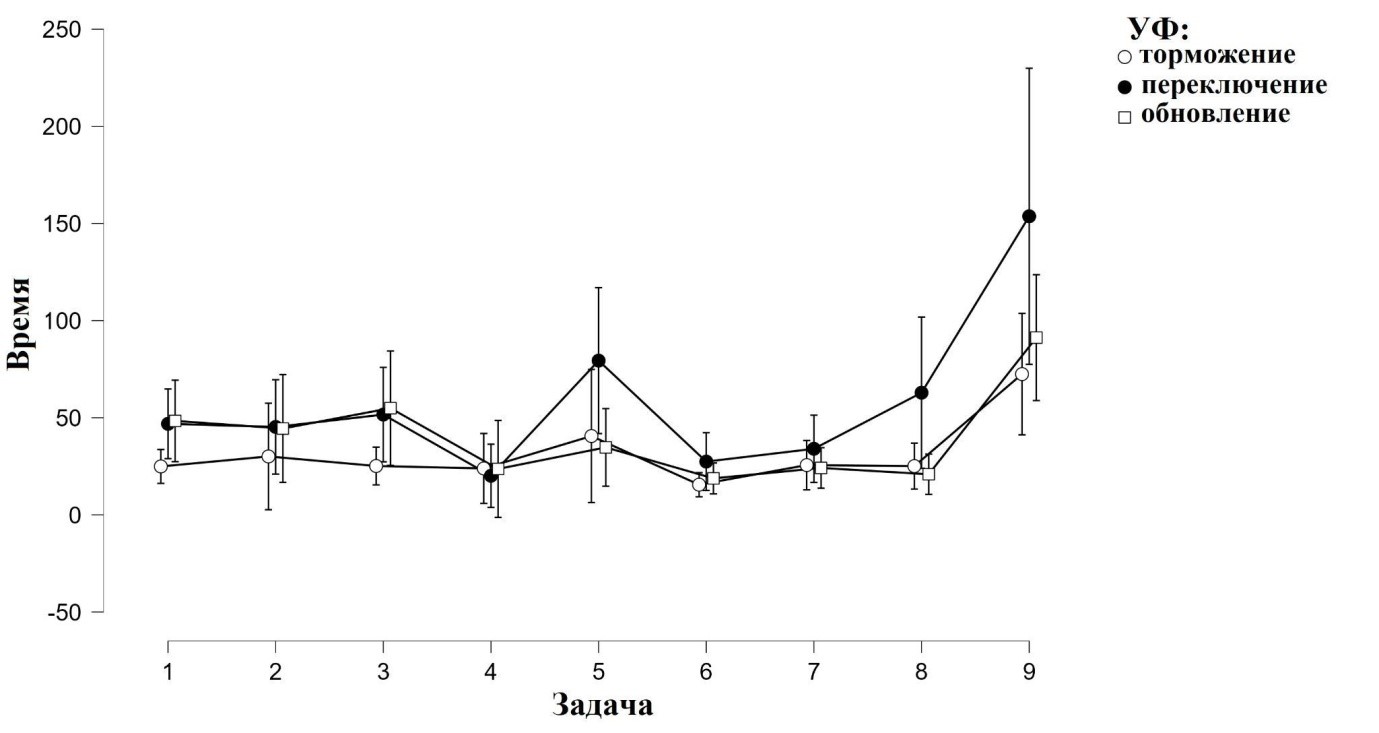
Отсутствует взаимодействие факторов тип загрузки и тип задачи, значимых различий в динамике формирования серии в условиях разной параллельной загрузки не выявлено, F (16; 448) = 1,44, p = 0,118, η2p = 0,049 (см. рис. 7).

Рис. 7. Время решения (в секундах) задач вербальной серии в условиях различной параллельной загрузки УФ

При анализе времени решения установочных задач серии (с 1 по 8) были выявлены значимые различия только для функции переключения: F (7; 133) = 2,846, p = 0,008, η2p = 0,13. Таким образом, в процессе решения установочных задач только загрузка переключения влияла на процесс формирования схемы решения задачи (см. рис. 7). Стоит отметить, что, если для арифметической серии различия во времени решения установочных задач демонстрируют научение и уменьшение времени от 1 к 8 задаче (см. рис. 6 и табл. 2), то для вербальной серии различия во времени решения установочных задач скорее демонстрируют влияние параллельной загрузки на автоматизацию схемы решения задачи (см. рис. 7).

Исходя из анализа времени решения последней установочной (восьмой) и критической (девятой) задач, значимые различия сохранялись в условиях торможения и обновления (см. табл. 4), то есть эффект серии сформировался. Однако в условиях с загрузкой переключения время решения последней установочной и критической задач значимо не различается (см. табл. 4), таким образом, в данных условиях эффект серии не сформировался.

Таблица 4. Анализ различий между временем решения последней установочной (восьмой) и критической (девятой) задачами в условиях различной параллельной загрузки УФ. Вербальная серия

 Анализ сложности параллельной загрузки УФ

Для дальнейшего анализа и интерпретации данных важно отметить, что время выполнения параллельных заданий на загрузку отдельных УФ значимо различается, F (2; 114) = 126,626, p < 0,001, η2p = 0,69. Самым сложным является задание на переключение, далее по сложности идет задание на обновление, а затем на торможение. Время выполнение задания на переключение значимо выше, чем время выполнения заданий на торможение (t (38) = –12,28, p < 0,001, Cohen's d = –1,966) и обновление (t (38) = 11,151, p < 0,001, Cohen's d = 1,786); в свою очередь, время выполнения заданий на обновление было значимо выше, чем время выполнения заданий на торможение (t (38) = –2,625, p = 0,012, Cohen's d = –0,42) — см. табл. 5.

Таблица 5. Среднее время выполнения вторичных задач

Обсуждение результатов

Результаты данного эксперимента изменили наши представления о роли отдельных УФ в процессе формирования эффекта серии. Мы предполагали, что формирование фиксированной схемы решения задачи требовательно к ресурсам таких управляющих функций, как переключение и обновление, а их дополнительная загрузка негативно скажется на формировании эффекта серии, так как вступит с процессом формирования устойчивой схемы решения в конкуренцию за специфический ресурс УФ. Однако загрузка переключения негативно повлияла на формирование эффекта серии только в вербальных задачах. В свою очередь, параллельная загрузка УФ любого типа не помешала формированию эффекта серии на материале арифметических задач и, скорее, усилила фиксацию на неверной схеме решения.

УФ в процессе формирования эффекта серии на материале арифметических задач

Если ранее было продемонстрировано, что сложная загрузка и переключение с одного материала на другой оказывает разрушающее воздействие на эффект серии на материале арифметических задач Лачинсов [Владимиров, 2018], то в данном исследовании загрузка отдельных УФ любой сложности и любого типа не повлияла на формирование эффекта. Как сложная загрузка переключения, так и более простые вторичные задания на обновление и торможение привели к тому, что схема решения “схватывалась” примерно к третьей задаче (см. рис. 6). Мы предполагаем, что в данном случае происходит когнитивная перегрузка [Котюсов, 2023; Fox, 2007], поскольку основная задача требовательна к УФ, также как и вторичная. Перегрузка УФ, в свою очередь, вызывает усиление фиксации, поскольку ресурсы смещаются с основной задачи на вторичную – это мешает рассматривать другие варианты решения основной задачи. Параллельная вторичная задача начинает рассматриваться, как основная и возникает повышенная потребность минимизировать энергетические затраты хотя бы на одно из параллельно выполняемых действий. Эффект перегрузки УФ может быть по своим механизмам похож на реакцию организма на стресс, поскольку активность смещается с префронтальной коры на подкорковые структуры, а с поведенческой точки зрения, на передний план выходят ранее автоматизированные или подкрепленные реакции [Arnsten, 2009]. Таким образом, положительная обратная связь от экспериментатора при решении первых задач серии ведет к тому, что подкрепление и схватывание схемы решения происходит быстрее. Стресс может служить для закрепления успешного поведения [Wickens, 2007]; усиливать долговременную память для стимулов, подкрепленных ранее положительной обратной связью [Lighthall, 2013]; вызывать ускоренное научение [Александров, 2017; Joëls, 2006; Sandi, 1997]. В данном контексте нельзя не упомянуть исследование С. Бейлока и М. ДеКаро [Beilock, 2007], в котором было показано, что люди с высоким уровнем рабочей памяти в стрессовых условиях склонны решать критическую задачу Лачинсов на переливание установочным способом. В целом, в стрессовых условиях люди становятся более ригидными [Beilock, 2007; Cowen, 1952; Luchins, 1942]. В работе Н.Х. Тухтиевой [Тухтиева, 2013] было показано, что регулярные изменения условий предъявления арифметических задач Лачинсов оказывали положительный эффект на снижение фиксации на материале арифметических задач Лачинсов, что соотносится с данными И.Ю. Владимирова и коллег [Владимиров, 2018]; при этом, нерегулярные хаотичные изменения, напротив, вызывали усиление фиксации. Н.Х. Тухтиева связывает данные результаты с механизмами изменения сознательного контроля; хаотические изменения провоцируют перефокусировку на решение дополнительной задачи, вследствие чего испытуемому сложно расфиксироваться и отойти от стереотипного поведения. В исследовании С.Ю. Коровкина и А.О. Рысь [Коровкин, 2023] к усилению фиксации привело изменение освещенности во время решения критических задач серии (включение света). Авторы также связывают полученные результаты с повышенной нагрузкой на внимание и перегрузкой РП, в связи с чем испытуемые начинают пользоваться автоматизированными схемами чаще.

УФ в процессе формирования эффекта серии на материале вербальных задач

Сложная параллельная загрузка переключения повлияла на формирование эффекта серии только на материале вербальных задач. Различия влияния параллельной загрузки отдельных УФ на формирование эффект серии на разном стимульном материале, во-первых, может быть связаны со спецификой схватывания установочной схемы решения, во-вторых, с высокой сложностью задания на переключение.

Так, установочная схема решения на материале вербальных задач не требует плавного научения в отличие от серии арифметических задач, установка на поиск слова в начале строки схватывается испытуемыми сразу, с первой задачи (см. рис. 7). Вырабатываемая на материале вербальных задач установка экологична опыту испытуемых, в частности, чтению сначала строки слева направо, поэтому автоматизируется достаточно быстро. Сами по себе вербальные задачи проще, усвоение схемы решения на вербальном материале, по всей видимости, осуществляется имплицитно [Деева, 2021], сама схема абстрактна, ее формирование менее требовательно к ресурсам УФ. Мы предполагаем, что в силу специфики формирования эффекта серии на вербальных задачах сложная загрузка приводит к ослаблению фиксации, так как не происходит перегрузки УФ, уровень загрузки УФ оптимальный [Владимиров, 2018; Тухтиева, 2013].

Выводы

Итак, в данном исследовании было продемонстрировано, что вопрос о механизмах формирования эффекта серии ещё далек от разрешения. Исходя из полученных данных, а также анализа литературы, есть основания предполагать, что при формировании эффекта серии повышение загрузки УФ может привести к двум противоположным эффектам — усилению и ослаблению фиксации. Активация УФ при формировании схемы решения задачи подчинена закону оптимума. В условиях слабой загрузки УФ фиксированность формируется [40 и мн. др.]; повышение загрузки УФ ведет к тому, что влияние установки на решение критической задачи снижается [Владимиров, 2018; Тухтиева, 2013]; однако при перегрузке УФ происходит усиление фиксации [8; 15; 23; 25; 36; 40 и др.]. Исходя из результатов исследования, мы полагаем, что общий уровень загрузки УФ (основная задача + вторичная задача), а не тип загрузки УФ (отдельно торможение, переключение или обновление) играет ключевую роль в процессе формирования эффекта серии.

Полученные результаты позволяют наметить следующие перспективы дальнейшей работы: во-первых, рассмотреть влияние фактора длины установочной серии на процесс формирования эффекта в условиях загрузки УФ [Crooks, 2009; Luchins, 1942; Tresselt, а]; во-вторых, рассмотреть процесс формирования эффекта серии еще на ещё одном классе задач – пространственных лабиринтах [Luchins, 1942]. Понимание специфики формирования фиксированных схем решения задач на различном стимульном материале в дальнейшем может лечь в основу рекомендаций и программ по профилактике трудностей в обучении [Исаев, 2023]; в-третьих, исследовать вклад УФ на различных этапах формирования эффекта серии, то есть отдельно на этапе формирования схемы решения, на этапе ее автоматизированного функционирования и на этапе её разрушения [Лазарева, 2024]; в-четвертых, рассмотреть влияние фактора осознаваемости схемы решения на процесс формирования эффекта серии и загрузку УФ [Деева, 2021]; в-пятых, рассмотреть возможности применения методов нейровизуализации и нейростимуляции в данной области исследований [Паникратова, 2022].

1. Александров Ю.И., Сварник О.Е., Знаменская И.И., Арутюнова К.Р., Колбенева М.Г., Крылов А.К., Булава А.И. Стресс, болезнь и научение как условия регрессии // Вопросы психологии. 2017. № 4. С. 87–101.
2. Асмолов А.Г. По ту сторону сознания: методологические проблемы неклассической психологии. М.: «Смысл», 2002. 480 с.
3. Величковский Б.Б. Функциональная организация рабочей памяти: дис. д-ра психол. наук. М., 2017. 340 с.
4. Владимиров И.Ю., Карпов А.В., Лазарева Н.Ю. Роль управляющего контроля и подчиненных систем рабочей памяти в формировании эффекта серии // Экспериментальная психология. 2018. Т. 11. № 3. С. 36–50. DOI:10.17759/exppsy.2018110303
5. Деева Т.М., Козлов Д.Д. Формирование абстрактного знания при имплицитном усвоении схемы решения анаграмм // Экспериментальная психология. 2021. Т. 14. № 1. C. 95–107. DOI:10.17759/exppsy.2021140103
6. Исаев Е.И., Марголис А.А. Трудности в обучении: диагностика, профилактика, преодоление // Психологическая наука и образование. 2023. Т. 28. № 5. C. 7–20. DOI:10.17759/pse.202328050
7. Козлов К. С., Горбунова Е. С. Загрузка рабочей памяти и перцептивное сходство при решении задач зрительного поиска множественных стимулов // Экспериментальная психология. 2019. Т. 12. №. 3. С. 119–134. doi:10.17759/exppsy.2019120309
8. Коровкин С.Ю., Рысь А.О. Изменение освещенности влияет на формирование мыслительной установки // Личность, интеллект, метакогниции: исследовательские подходы и образовательные практики. Материалы III-й Всероссийской научно-практической конференции 20-22 апреля 2023 г., Калуга, Россия. Калуга, 2023. С. 30–38.
9. Котюсов А.И. Рабочая память и внимание при когнитивной перегрузке: индивидуальные различия и динамика нейрокогнитивных характеристик: дисс. … канд. психол. наук. Екб., 2023. 147 с.
10. Лазарева Н.Ю. Роль рабочей памяти в процессе формирования эффекта серии и возникновении инсайтного решения: дисс. … канд. психол. наук. М., 2024. 234 с.
11. Лазарева Н.Ю., Чистопольская А.В., Анфалова С.В. Разработка невербального зонд-задания для загрузки управляющей функции торможения рабочей памяти // Ярославский психологический вестник. Учредители: Российское психологическое общество. 2022. № 1(52). С. 48–52.
12. Лазарева Н.Ю., Владимиров И.Ю. Механизмы творческого решения задач: влияние предварительной установки на возникновение инсайтного решения // Психология состояний человека: актуальные теоретические и прикладные проблемы [Электронный ресурс]: сборник материалов IV Всероссийской научной конференции с международным участием (Казань, 8–10 ноября 2023 г.) / ред. кол.: А.О. Прохоров, Б.С. Алишев, А.В. Чернов, М.Г. Юсупов. Электронные текстовые данные (1 файл: 1,40 Мб). Казань: Издательство Казанского университета, 2023. С. 379–383.
13. Паникратова Я.Р., Власова Р.М., Лебедева И.С., Синицын В.Е., Печенкова Е.В. Возможности методов нейровизуализации и нейростимуляции для развития теории системной динамической локализации высших психических функций // Культурно-историческая психология. 2022. Т. 18. № 3. С. 70–80. DOI:10.17759/chp.2022180310
14. Савинова А.Д., Коровкин С.Ю. Как связаны рабочая память и изменение репрезентации: специфический и неспецифический подход к инсайту // Экспериментальная психология. 2023. Т. 16. № 4. С. 36–56. DOI:10.17759/exppsy.2023160403
15. Тухтиева Н.Х. Влияние иррелевантных параметров задач на эффект установки (на примере эффектов Лачинса и Узнадзе): дисс. … канд. психол. наук. Спб., 2013. 168 с.
16. Фаликман М.В. Эффекты превосходства слова в зрительном восприятии и внимании // Психологический журнал. 2010. Т. 3. № 1. С. 32–40. 
17. Ach N. Über den Willensakt und das Temperament: eine experimentelle Untersuchung. Quelle & Meyer, 1910.
18. Aftanas M.S., Koppenaal R.J. Effects of instructional problems and jar position variation on the water-jar Einstellung test // Psychological Reports. 1962. Vol. 10. № 2. P. 359–362. DOI:10.2466/pr0.1962.10.2.359
19. Arnsten A.F. Stress signalling pathways that impair prefrontal cortex structure and function // Nature reviews neuroscience. 2009. Vol. 10. № 6. P. 410–422. DOI:10.1038/nrn2648
20. Baddeley A.D. Exploring the central executive // Exploring Working Memory. Routledge, 2017. P. 253–279.
21. Baddeley A.D. Is working memory still working? // European Psychologist. 2002. 7. № 2. P. 85–97. DOI:10.1027/1016-9040.7.2.85
22. Baddeley A.D., Hitch G.J. Working memory // The psychology of learning and motivation. 1974. Vol. Р. 47–89.
23. Beilock S.L., DeCaro M.S. From poor performance to success under stress: working memory, strategy selection, and mathematical problem solving under pressure // Journal of Experimental Psychology: Learning, Memory, and Cognition. 2007. Vol. 33. № 6. P. 983–998. DOI:10.1037/0278-7393.33.6.983
24. Cowan N. An embedded-processes model of working memory // Models of working memory: Mechanisms of active maintenance and executive control. 1999. 20. № 506. P. 1013–1019. DOI:10.1017/CBO9781139174909.006
25. Cowen E.L. Stress reduction and problem-solving rigidity // Journal of Consulting Psychology. 1952. Vol. 16. № 6. P. 425–428. DOI:1037/h0060888
26. Crooks N.M., McNeil N.M. Increased practice with “set” problems hinders performance on the water jar task // Proceedings of the Annual Meeting of the Cognitive Science Society. 2009. Vol. 31. № 31. DOI:10.1007/s10339-023-01141-5
27. Fox J.R., Park B., Lang A. When available resources become negative resources: The effects of cognitive overload on memory sensitivity and criterion bias // Communication Research. 2007. 34. № 3. P. 277–296. DOI:10.1177/00936502073004
28. Guetzkow H. An analysis of the operation of set in problem-solving behavior // The Journal of General Psychology. 1951. Vol. 45. № 2. P. 219–244. DOI:10.1080/00221309.1951.9918281
29. Jacobus K.A., Johnson N.F. An experimental set to adopt a set // Psychological Reports. 1964. DOI:10.2466/pr0.1964.15.3.737
30. Jensen J. On the Einstellung effect in problem solving: Some critical remarks // Scandinavian Journal of Psychology. 1960. Vol. 1. № 1. P. 163–168. DOI:10.1111/j.1467-9450.1960.tb01295.x
31. Joëls M., Pu Z., Wiegert O., Oitzl M.S., Krugers H.J. Learning under stress: How does it work? // Trends in Cognit. Sci. 2006. Vol. 10. № 4. P. 152–158. DOI:10.1016/j.tics.2006.02.002
32. Juola J.F., Hergenhahn B.R. Effects of overtraining on the establishment of mental set in anagram solving // Psychonomic Science. 1967. Vol. 9. № 10. P. 539–540. DOI:10.3758/BF03327878
33. Juola J.F., Hergenhahn B.R. Effects of training level, type of training, and awareness on the establishment of mental set in anagram solving // The Journal of Psychology. 1968. Vol. 69. № 2. P. 155–159. DOI:10.1080/00223980.1968.10543460
34. Kahneman D. Attention and Effort. Englewood Cliffs, NJ: Prentice Hall, Inc., 1973.
35. Kendler H.H., Greenberg A., Richman H. The influence of massed and distributed practice on the development of mental set // Journal of Experimental Psychology. 1952. Vol. 43. № 1. P. 21–25. DOI:10.1037/h0056909
36. Knight K.E. Effect of effort on behavioral rigidity in a Luchins water jar task // The Journal of Abnormal and Social Psychology. 1963. Vol. 66. № 2. P. 190–192. DOI:1037/h0046874
37. Korovkin S. The role of working memory at different stages of insight problem solving: a critical review // Psychology. Journal of Higher School of Economics. 2023. Vol. 20. № 3. P. 407–417. DOI:10.17323/1813-8918-2023-3-407-417
38. Korovkin S., Vladimirov I., Chistopolskaya A., Savinova A. How working memory provides representational change during insight problem solving // Frontiers in Psychology. 2018. Vol. 9. № 1864. P. 1–16. DOI:10.3389/fpsyg.2018.01864
39. Lighthall N.R., Gorlick M.A., Schoeke A., Frank M.J., Mather M. Stress modulates reinforcement learning in younger and older adults // Psychology and aging. 2013. Vol. 28. № 1. P. 35–46. DOI:10.1037/a0029823
40. Luchins A.S. Mechanization in problem solving: The effect of Einstellung // Psychological Monographs. 1942. Vol. 54. № 6. P. 95. DOI:1037/h0093502
41. Luchins A.S., Luchins E.H. New experimental attempts at preventing mechanization in problem solving // The Journal of General Psychology. 1950. Vol. 42. № 2. P. 279–297. DOI:10.1080/00221309.1950.9920160
42. Maltzman I., Fox J., Morrisett Jr L. Some effects of manifest anxiety on mental set // Journal of Experimental Psychology. 1953. Vol. 46. № 1. P. 50–54. DOI:10.1037/h0057448
43. Miyake A., Friedman N.P., Emerson M.J., Witzki A.H., Howerter A., Wager T.D. The unity and diversity of executive functions and their contributions to complex “frontal lobe” tasks: A latent variable analysis // Cognitive psychology. 2000. Vol. 41. № 1. P. 49–100. DOI:1006/cogp.1999.0734
44. Oberauer K. Working memory and attention–A conceptual analysis and review // Journal of cognition. 2019. 2. № 1. DOI:10.5334/joc.58
45. Reber P.J., Kotovsky K. Implicit learning in problem solving: The role of working memory capacity // Journal of Experimental Psychology: General, 1997. Vol. № 2. P. 178–203. DOI:10.1037/0096-3445.126.2.178
46. Rees H.J., Israel H.E. An investigation of the establishment and operation of mental sets // Psychological Monographs. 1935. Vol. 46. № P. 1–26. DOI:10.1037/h0093375
47. Sandi C., Loscertales M., Guaza C. Experience‐dependent facilitating effect of corticosterone on spatial memory formation in the water maze // European journal of neuroscience. 1997. Vol. 9. № 4. P. 637–642. DOI:10.1111/j.1460-9568.1997.tb01412.x
48. Savinova A., Padalka J., Makarov I., Korovkin S. Tracing executive functions in insight // The Journal of General Psychology. 2023. P. 1–25. DOI:1080/00221309.2
49. Tresselt M.E., Leeds D.S. The effect of concretizing the mental set experiment // The Journal of General Psychology. 1953a. Vol. 48. № 1. P. 51–55. DOI:10.1080/00221309.1953.9920173
50. Tresselt M.E., Leeds D.S. The Einstellung effect in immediate and delayed problem-solving // The Journal of General Psychology. 1953b. Vol. 49. № 1. P. 87–95. DOI:10.1080/00221309.1953.9710679
51. Vallée-Tourangeau F., Euden G., Hearn V. Einstellung defused: Interactivity and mental set // The Quarterly Journal of Experimental Psychology. 2011. Vol. 64. № 10. P. 1889–1895. DOI:10.1080/17470218.2011.605151
52. Van Stockum Jr C.A., DeCaro M.S. When working memory mechanisms compete: Predicting cognitive flexibility versus mental set // Cognition. 2020. Vol. 201. P. 104313. DOI:10.1016/j.cognition.2020.104313
53. Wickens J.R., Horvitz J.C., Costa R.M., Killcross S. Dopaminergic mechanisms in actions and habits // Journal of Neuroscience. 2007. Vol. 27. № 31. P. 8181–8183. DOI:10.1523/JNEUROSCI.1671-07.2007