Введение
В экспериментальной психологии и психофизиологии для ряда исследований актуальна задача анализа динамики связи временных рядов поведенческих (таких, как время ответа или результативность решения задач) и физиологических (амплитудно-временные характеристики компонентов связанных с событием потенциалов (ССП), выраженность спектров электроэнцефалограммы (ЭЭГ) и др.) показателей. Взаимосвязь между временными рядами, которые отражают те или иные психические и/или физиологические феномены, имеющие процессуальный характер, может быть различной в силу неоднородности протекания этих процессов (неоднородность и нестационарность (свойство временного ряда изменять свои характеристики с течением времени) протекания психических феноменов, имеющих процессуальный характер, неоднократно подчеркивалась в литературе (Барабанщиков, 1990; Знаков, 2024; Костин, Голиков, 2010; Садов, 1982)). Поэтому, помимо задачи общей оценки взаимосвязи между временными рядами, актуальной является также оценка динамики этой взаимосвязи, то есть оценка изменений взаимосвязи между рядами в ходе экспериментальной процедуры.
Анализ временных рядов разрабатывался во многих научных сферах (Keogh, Kasetty, 2003), но традиционно эта проблема освещалась в эконометрике для анализа финансового рынка. В эконометрике существует ряд специфик анализируемых данных: неэкспериментальный характер полученных данных, сильная вариабельность единиц измерения, проблема не стандартизированного измерительного инструмента (Галочкин, 2021). Из-за этого применение статистических методов, разработанных в эконометрике, может быть затруднительным для использования в психологических и психофизиологических исследованиях.
Традиционно при анализе временных рядов решаются разные задачи: выявление трендов во временных рядах, прогнозирование, кластеризация временных рядов, задача сегментирования временных рядов, уменьшение размерности временных рядов, задача поиска связи между временными рядами (Keogh, Kasetty, 2003).
Для задачи прогнозирования стационарных временных рядов используется модель авторегрессии — скользящего среднего (ARMA) или ARMAX-модель. В данных моделях высчитываются скользящие средние (moving average) с определенным шагом усреднения, которое рассматривается как белый шум (случайные стационарные колебания в определенном диапазоне), а предсказание движения временного ряда выводится на основании авторегрессии с учетом изменения скользящего среднего значения в стационарном ряду (Brockwell, Davis, 2016). Для прогнозирования нестационарных временных рядов используются ARIMA- и ARFIMA-модели, которые предполагают преобразование нестационарных рядов в стационарные при помощи интегративных методов, позволяющих выявлять закономерности в нестационарном временном ряду (Fenga, 2017). Помимо этого, данные модели могут учитывать сезонность временных рядов. Сезонность в этих моделях может закладываться априорно в зависимости от времени года или высчитываться эмпирически, исходя из автокорреляционной функции временного ряда (сезонность как цикличность колебаний, встречающихся во временном ряду).
Методы прогнозирования используются повсеместно в эконометрике и в data science, но мало пригодны для психологических и психофизиологических исследований. Данные методы применяются для анализа экономических показателей, измеренных на протяженной дистанции времени (дни, месяцы, годы), в отличие от большей части психологических и психофизиологических исследований, где, к примеру, временной ряд в 500 проб фиксируется в рамках одного часового эксперимента. Что еще более важно, из-за характера получаемых экспериментальных данных в психологии и отсутствия априорной цикличности выявление сезонности временных рядов является необоснованным и затруднительным для анализа данных. Кроме того, методы прогнозирования несут исключительно практический или прикладной характер, тогда как в фундаментальной психологии более актуальной является задача теоретического объяснения анализируемых временных рядов, и их прогнозирование не даст такого практического результата, как в эконометрике.
Для задачи кластеризации нескольких временных рядов с целью их классификации используют нестандартные метрики, специфичные для анализа именно временных рядов (Paparrizos et al. 2024). Помимо классической евклидовой метрики, для кластеризации временных рядов используют: минимальную прыжковую стоимость (Minimum Jump Cost) (Serrà, Arcos, 2012), динамическую трансформацию временной шкалы (Dynamic Time Warping) (Marteau, 2009), длиннейший общий отрезок (Longest Common Distance), кросс-корреляции, дискретное расстояние Фреше (оно же сцепленное расстояние), расстояние с поправкой на сложность (Complexity Invariant Distance) (Gustavo et al. 2011), расстояние с поправкой на взаимную компрессию (Compression Rate Distance) (Vo, Duong, 2015), расстояние Махаланобиса (Dinkar et al. 2015) и др. Все эти метрики учитывают в той или иной мере возможный сдвиг между двумя временными рядами, но если, к примеру, кросс-корреляции учитывают единый фиксированный сдвиг на всей протяженности временного ряда, то динамическая трансформация временной шкалы выстраивает два временных ряда с нефиксированным (вариабельным) сдвигом, приводя два временных ряда к оптимальному соответствию (выявляя тождественность основных пиков и спадов двух временных рядов).
Все вышеупомянутые метрики для кластеризации нескольких временных рядов классифицируют данные на различных основаниях и имеют свои преимущества и недостатки, связанные с тем, что классификация идет на задавание временного лага. Модели, имеющие фиксированный временной лаг, не подходят для психологических и психофизиологических данных ввиду неоднородности протекания исследуемых процессов. В отличие от них, модели с динамическим лагом позволяют сопоставить между собой несколько неоднородных процессов. Однако кластеризация с динамическим лагом не позволяет делать статистические выводы относительно связи между временными рядами.
Задача поиска связи двух временных рядов менее разработана, нежели вышеописанные методы прогнозирования и классификации. Существующие методы, которые показывают связь двух временных рядов, имеют ряд недостатков. Классический метод, используемый для анализа связи двух временных рядов — кросс-корреляции, — подсчитывает связь двух временных рядов с учетом фиксированного сдвига в данных, из-за этого он не подходит в ситуациях, когда сдвиг двух временных шкал также варьируется. Среди более современных методов выделяется метод минимальной прыжковой стоимости (Minimum Jump Cost), который учитывает только прямые связи между временными рядами (Serria, Arcos, 2012). Помимо этого, все проанализированные нами методы, показывающие связанность двух временных рядов, учитывают связь на всем диапазоне данных, а не динамику связи двух временных рядов во времени.
В силу того, что временные ряды в экспериментально-психологических и психофизиологических исследованиях зачастую обладают свойством нестационарности (Kislitsyn, 2019), необходимо проведение оценки связности не только и не столько временных рядов по совокупности, сколько на отдельных эпохах анализа. В условиях работы с нестационарными временными рядами возможны ситуации, при которых в одних эпохах анализа будут наблюдаться прямые взаимосвязи, в других — обратные, в третьих — отсутствие линейных связей.
Для решения поставленной задачи нами предлагается метод «скользящего окна» с задаваемой исследователем шириной окна и шагом окна.
Ковариационный анализ методом «скользящего окна»
Для оценки динамики связи временных рядов нами применялся ковариационный анализ методом «скользящего окна», позволяющий последовательно включать в анализ точки из временных рядов заданного количества и с заданным шагом окна. Это позволяет говорить о том, что на той или иной эпохе анализа наблюдаются синхронные изменения анализируемых показателей. Для примера в данной работе диапазон усреднения задавался нами в 50 проб, а шаг окна — в одну пробу (рис. 1). Параметры (в особенности — ширина окна) могут зависеть от специфики анализируемых данных, шаг в одну пробу позволяет добиваться наибольшей информативности при анализе динамики взаимосвязи между рядами. Шаг окна меньший, чем его ширина, с одной стороны, приводит к пересекаемости между анализируемыми эпохами анализа, а с другой — позволяет опосредованно учесть вклад каждой точки временного ряда и выявить точки демаркации, относительно которых возможно описание связности отдельных эпох временных рядов.
Ковариационный анализ, в отличие от корреляционного, позволяет не только оценивать направленность связи, но и показывает выраженность совместной динамики двух анализируемых рядов. Это связано с тем, что корреляция является безразмерной величиной, а ковариация имеет единицу измерения, выраженную произведением единиц измерения анализируемых величин. Таким образом, значения ковариаций позволяют дифференцировать фрагменты временных рядов, где наблюдалась более выраженная динамика, от фрагментов, где наблюдалась менее выраженная динамика.
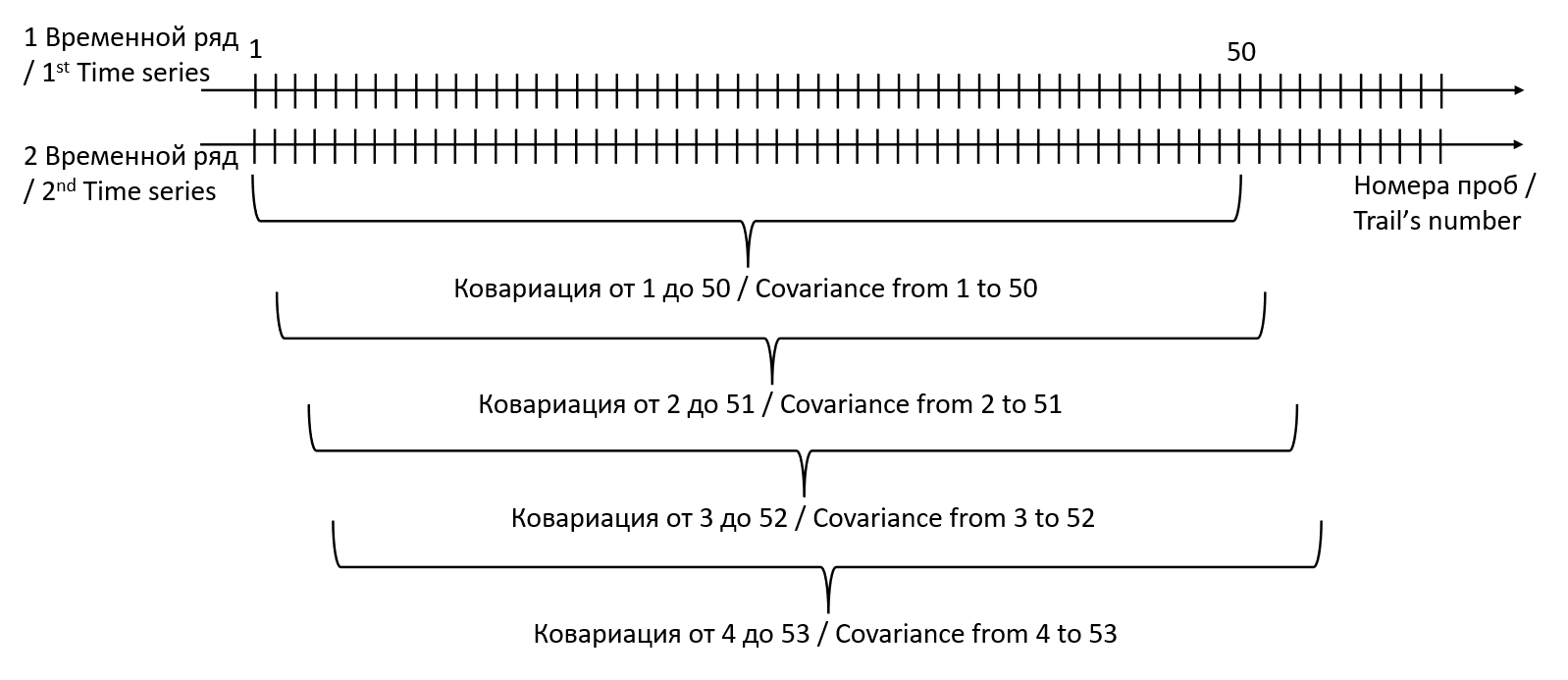
Рис. 1. Принцип расчета ковариации методом «скользящего окна» по 50 проб с шагом в 1 пробу
Fig. 1. Principle of calculating covariance using the “moving average” method for 50 trials with a step of 1 trial
Для проверкии описания данного метода использовались смоделированные данные (рис. 2), которые включают в себя эпохи разной степени связности и с различной динамикой (более выраженной и менее выраженной). В модель закладывались тренды (увеличение/уменьшение показателя по одному из двух рядов); для того, чтобы данные были приближены к реальным, помимо тенденций был заложен «шум», представленный значениями нормального распределения с задаваемым стандартным отклонением относительно закладываемых трендов (Гауссов шум). Целью применения такого уровня моделирования было сопоставление корреляционного и ковариационного анализов с применением метода «скользящего окна».
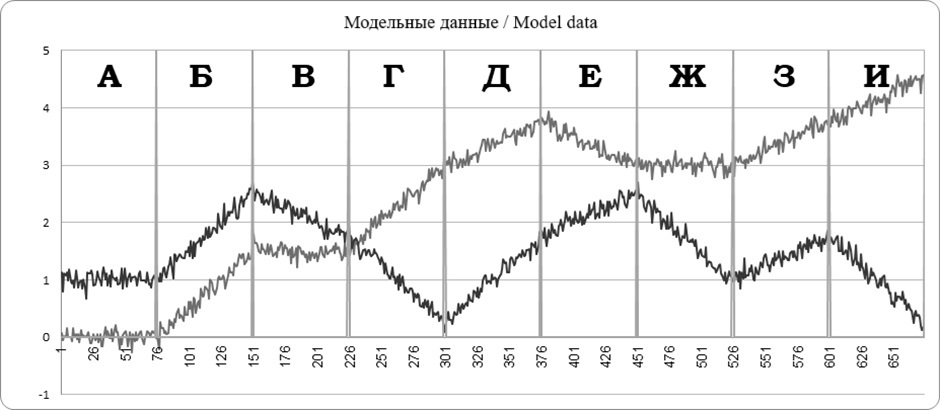
Рис. 2. Смоделированные данные. Серым и черным цветом отмечены временные ряды. Буквами отмечены описанные выше эпохи: по оси абсцисс указан номер усреднения, по оси ординат — выраженность показателей временных рядов
Fig. 2. Simulated data. Time series are marked in gray and black. The periods described above are marked with letters: the x-axis shows the averaging number, and the y-axis shows the severity of the time series indicators
В модель (рис. 2) были заложены следующие эпохи:
А — отсутствие динамики по обоим рядам («плато»);
Б — общая выраженная однонаправленная динамика показателей;
В — невыраженная динамика по первому ряду и «плато» по второму ряду;
Г — общая выраженная разнонаправленная динамика показателей;
Д — однонаправленная динамика по обоим показателям, но выраженность динамики высока только по одному из двух рядов;
Е — невыраженная разнонаправленная динамика показателей;
Ж — выраженная динамика по первому ряду и «плато» по второму ряду;
З — общая невыраженная динамика показателей;
И — разнонаправленная динамика по обоим показателям, но выраженность динамики высока только по одному из двух рядов.
Все перечисленные эпохи имели длительность в 75 точек, ковариации, как было описано выше, рассчитывались по 50 точкам с шагом в 1 точку. Таким образом, на каждую эпоху приходилось по 25 значений ковариаций, которые рассчитывались по диапазону, не пересекающемуся с другими эпохами.
В тех окнах ковариационного анализа, которые будут целиком захватывать эпоху, ожидается получить более «чистые» тренды. Окна, которые включают в себя две или, потенциально, более эпох, будут непоказательными. На рис. 3. выделены зоны, где ковариация включала точки, принадлежащие одной и той же эпохе. Соответственно, в интервалах, включающих более одной эпохи, ковариации стремятся к нулю.
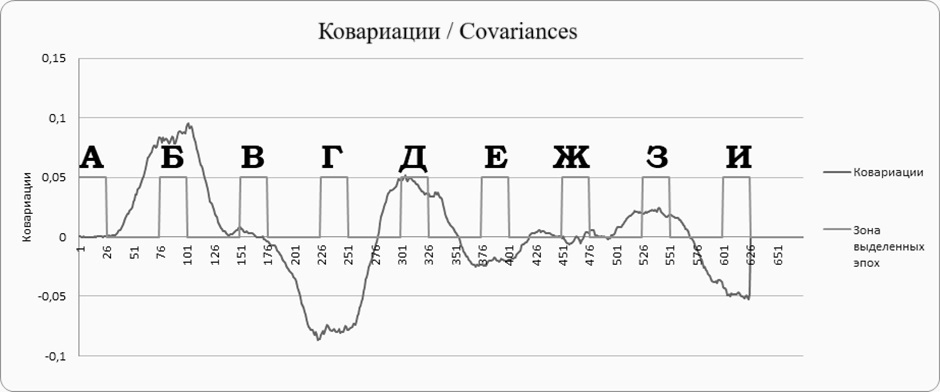
Рис. 3. Ковариации, построенные методом «скользящего окна»: по оси абсцисс указан номер усреднения, по оси ординат — выраженность ковариаций
Fig. 3. Covariances constructed using the “moving average” method: the x-axis shows the averaging number, and the y-axis shows the severity of the covariances
Как можно увидеть на рис. 3, эпохам, где хотя бы один ряд (В, Ж) или оба ряда (А) были представлены «плато», соответствуют стремящиеся к нулю ковариации. Эпохе с высокой однонаправленной динамикой показателей (Б) соответствуют высокие положительные значения ковариаций. Эпохе с высокой разнонаправленной динамикой (Г) — высокие отрицательные значения ковариаций. Эпохе с высоким однонаправленным ростом по одному показателю и низким ростом по второму (Д) — средние положительные значения ковариаций. Эпохе с низкой разнонаправленной динамикой показателей (Е) — низкие отрицательные значения ковариаций. Эпохе с низкой однонаправленной динамикой показателей (З) — низкие положительные значения ковариаций. Эпохе с высоким разнонаправленным ростом по одному показателю и низким ростом по второму (И) — средние отрицательные значения ковариаций. Ковариации, которые включают в анализ пересекающиеся эпохи, стремятся к нулю.
К преимуществам данного метода можно отнести то, что окна ковариаций, находящиеся в одной эпохе, хорошо демонстрируют заложенные в смоделированные данные связи. Но стоит учитывать, что эпохи, их пересечения и непересечения могут в реальных данных приобретать разную ширину и последовательность.
Ковариации, подсчитанные с помощью метода «скользящего окна», показывают не связь как повторяемость двух временных рядов, а силу взаимных изменений двух временных рядов. Для данного метода возможна описанная нами ниже статистическая оценка достоверности взаимосвязи, которая базируется на модели Фишера (см. «Методы статистической оценки при проведении ковариационного анализа»).
Сопоставление ковариационного и корреляционного анализов
Надо отметить, что для коэффициента ковариации не были описаны принципы проверки статистических гипотез, аналогично коэффициенту корреляции. Это несколько затрудняет работу с данным показателем, и дальнейшая интерпретация может оцениваться только количественным методом. При этом применение коэффициента корреляции имеет в случае решения задачи анализа временных рядов существенные ограничения.
Коэффициент ковариации имеет единицы измерения, представленные произведением единиц измерения фрагментов рядов, вошедших в анализ, то есть ковариация отражает величину совместного изменения временных рядов. Корреляция не имеет размерности, связанной с масштабом включаемых в анализ данных, и поэтому корреляционный анализ не позволяет дифференцировать эпохи с существенным закономерным изменением показателей от эпох с невыраженной динамикой в том случае, если она закономерна. График «скользящего окна» корреляций на тех же самых смоделированных данных (рис. 4) показывает, что эпохи с динамикой разной выраженности представлены практически одинаковым высоким уровнем корреляций. Стремящиеся к модулю единицы корреляции наблюдаются как в случае с выраженным ростом показателей по обоим временным рядам (эпохи Б, Г), так и в случае с невыраженной динамикой (по одному (эпохи Д, И) и в меньшей степени обоими рядами (эпохи Е, З)), т. е. динамика разной выраженности в случае применения корреляционного анализа не дифференцируется. Ковариационный анализ дает дополнительную информацию о том, что связь временных рядов либо не является выраженной, либо общая динамика на данных эпохах существенно ниже, чем на эпохах с высокими значениями ковариаций.
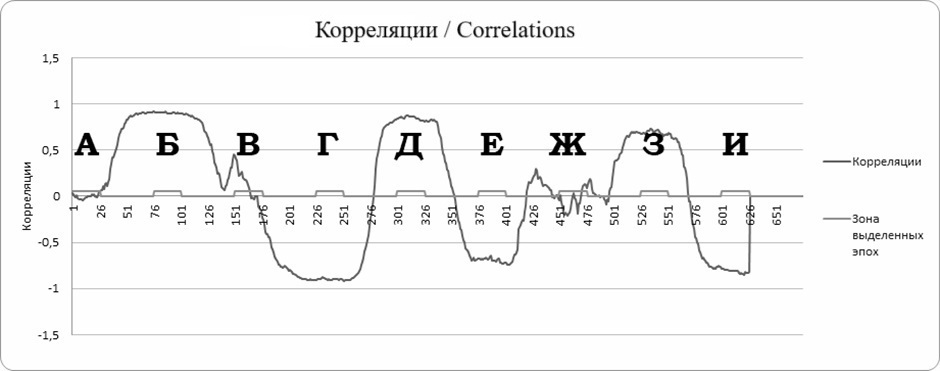
Рис. 4. Корреляции, построенные методом «скользящего окна»: по оси абсцисс указан номер усреднения, по оси ординат — выраженность корреляций
Fig. 4. Correlations constructed using the “moving average” method: the x-axis shows the averaging number, and the y-axis shows the severity of correlations
Важным аспектом при применении ковариационного анализа является соотношение «сигнал–шум». При моделировании данных на эпохи с разной степенью выраженности динамики накладывался Гауссов шум. Как было описано выше, Гауссов шум закладывался следующим образом: к описанным выше эпохам добавлялись значения нормального распределения с математическим ожиданием, равным нулю, и стандартным отклонением, значение которого соответствовало уровню шума, в процентах относительно разброса, закладываемого смоделированной динамикой.
При включении в модель шума разной степени интенсивности ковариационный и корреляционный анализ демонстрируют разную степень дифференцирования эпох с динамикой разной степени. В данном случае генерация шума производилась 100 раз (т. е. было 100 выборок смоделированных данных на каждый уровень шума); затем значения корреляций и ковариаций усреднялись для каждой из выбранных эпох.
При уровне шума, стремящемся к нулю, корреляционный анализ (рис. 5, Б) показывает крайне высокие степени взаимосвязи в эпохах анализа Б (выраженный рост по обоим показателям), Д (выраженный рост по одному показателю и невыраженный по второму), З (невыраженный рост по обоим показателям). При увеличении уровня шума корреляции между временными рядами по этим же эпохам снижаются, и при чрезмерно высоком уровне шума взаимосвязи не наблюдаются, а данные ситуации снова становятся недифференцируемыми, на основе чего можно сделать вывод о невозможности различения данных ситуаций методом корреляционного анализа. Ковариационный анализ (рис. 5, А), напротив, демонстрирует большую устойчивость к изменению уровня шума (см. табл.).
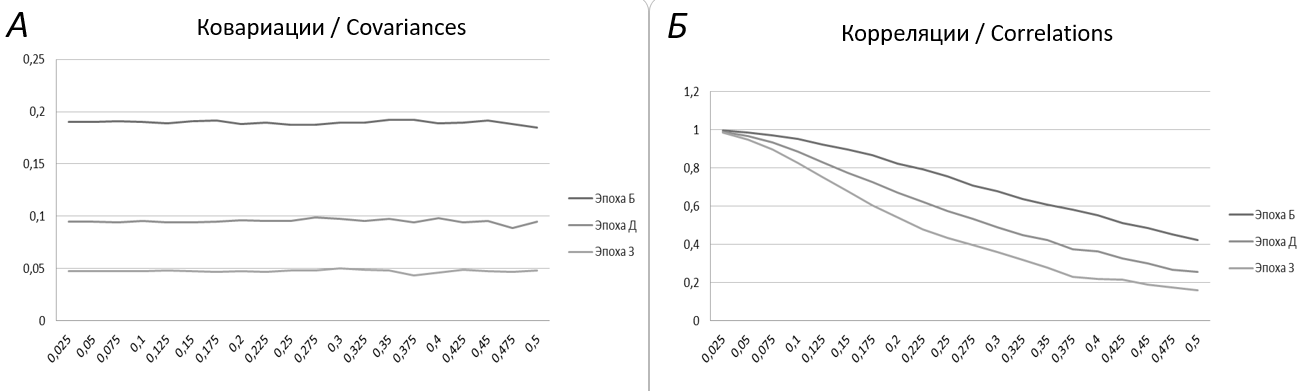
Рис. 5. Значения ковариаций и корреляций при разной степени шума: значение шума указано в относительных величинах относительно динамики, заложенной в смоделированных данных. По оси абсцисс указан уровень шума, по оси ординат — А: величина ковариаций; Б: величина корреляций
Fig. 5. Values of covariances and correlations at different noise levels: noise values are given in relative terms with respect to the dynamics embedded in the simulated data. The x-axis shows the noise level, while the y-axis shows A: covariance values; B: correlation values
Если проводить сопоставление ковариационного и корреляционного анализов, то можно говорить о том, что ковариационный анализ более чувствителен к тому, насколько выражена динамика временных рядов, а корреляционный — к уровню зашумленности, который опосредованно говорит о силе связи. Таким образом, при анализе сходства динамики двух временных рядов ковариационный анализ выглядит более предпочтительным.
Таблица
Сопоставление результатов ковариационного и корреляционного анализа
|
|
Слабый шум |
Средний шум |
Сильный шум |
|
Слабая совместная динамика |
r высокая cov низкая |
r средняя cov низкая |
r низкая cov низкая |
|
Средняя совместная динамика |
r высокая cov средняя |
r средняя cov средняя |
r низкая cov средняя |
|
Сильная совместная динамика |
r высокая cov высокая |
r средняя cov высокая |
r низкая cov высокая |
Примечание: r — корреляция, cov — ковариация.
Table
Comparison of the results of covariance and correlation analysis
|
|
Weak noise |
Average noise |
Strong noise |
|
Weak joint dynamics |
r high cov low |
r average cov low |
r low cov low |
|
Average joint dynamics |
r high cov average |
r average cov average |
r low cov average |
|
Strong joint dynamics |
r high cov high |
r average cov high |
r low cov high |
Note: r — correlation, cov — covariance.
Методы статистической оценки при проведении ковариационного анализа
Как было сказано выше, ковариационный анализ, в отличие от корреляционного, не имеет стандартного метода статистической проверки. Корреляционный анализ предполагает возможность тестирования гипотез H0 и H1, которые говорят о том, отличается ли достоверно коэффициент корреляции от нуля. Для решения этой проблемы возможно действовать несколькими способами. Во-первых, как было обозначено выше, ковариационный анализ имеет преимущество в том, что значения коэффициентов ковариации отражают уровень динамики, а не только наличие/отсутствие взаимосвязей. Соответственно, в определенных условиях и/или группах испытуемых возможно использование значений ковариаций как количественных данных для возможности анализа большей или меньшей степени связи (а не только для установления ее наличия/отсутствия). В том случае, если необходима статистическая оценка достоверности связей, возможно использование логики, задействованной из регрессионного анализа.
Для применения используемой в регрессионном анализе модели Фишера важно отметить, что данные должны соответствовать закону нормального распределения. Нами проводилась проверка на окнах усреднения в 50 точек, что представляется оптимальным: с одной стороны, оно является достаточно информативным, чтобы анализировать динамику взаимосвязей между временными рядами, также при анализе меньшего количества точек (к примеру, 30) шум может существенно перекрывать исходно заложенные связи. Вдобавок стоит отметить, что на малом объеме выборки критерии проверки соответствия распределения нормальному имеют тенденцию к неотвержению гипотезы о соответствии нормальному закону даже в случае существенных отклонений от формы нормальной кривой.
Таким образом, F-модель, показывающая достоверность объясненной дисперсии, будет выглядеть следующим образом:
со степенями свободы df1 = 1, df2 = n – 2. В этом случае проверяется гипотеза H0: MSрег ≤ MSост, которая отвергается в том случае, если значение F-статистики равно или превышает квантиль q0.95 F-распределения со степенями свободы df1 = 1; df2 = n – 2. В этом случае не отвергается гипотеза H1: MSрег > MSост и делается вывод о том, что взаимосвязь между двумя временными рядами в данном окне усреднения является достоверной.
Среди достоинств такого подхода статистической оценки можно отметить его возможное расширение на случай оценки связи между тремя и более временными рядами.
Сопоставление с реальными данными
Ковариационный анализ методом «скользящего окна» применяется авторами в рамках исследования универсальных закономерностей мозговых особенностей процесса научения (Юдаков и др., 2024; Apanovich et al., 2023). Данный метод анализа применялся для оценки динамики связи результативности решения задачи различения коротких интервалов времени с амплитудно-временными характеристиками компонентов ССП. На рис. 6, где показан пример сопоставления поведенческих данных с амплитудными характеристиками одного из выделенных компонентов ССП, видно, что метод способен выделять участки с прямой и обратной связью (А) и показывать выраженность этой связи (Б). Помимо наличия связи метод позволяет количественно выделить соотношение этой связи на всем диапазоне данных или на отдельном поведенческом сегменте в зависимости от целей исследования (например, посчитать соотношение прямых и обратных связей в ситуации случайного и неслучайного решения или оценить среднюю ковариацию в разные периоды экспериментальной ситуации).
К примеру, на рис. 6 видно, что результативность решения имеет обратные взаимосвязи с амплитудой позитивного компонента ССП до 40 точки и после 220, в промежутке между этими точками можно говорить о превалировании прямых взаимосвязей. В остальных промежутках превалируют обратные взаимосвязи.
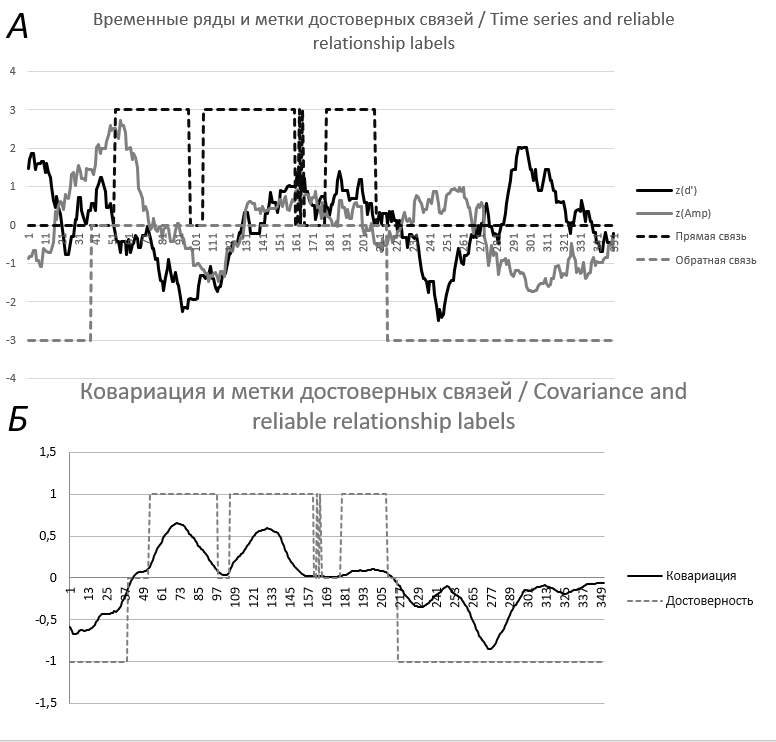
Fig. 6. Example of applying covariances constructed using the “moving average” method to empirical data.
Примечание: А. Черной линией отражается результативность в единицах d’, серой линией — амплитуда в микровольтах (для удобства отображения оба графика представлены в z-координатах). По оси абсцисс усредненное окно проб (от 1 до 351), по ординате выраженность результативности и амплитуды пика. Серой пунктирной линией отмечены участки с достоверной обратной связью, черной пунктирной линией отображены участки с достоверной прямой связью. Б. По оси абсцисс усредненное окно проб (от 1 до 351). По ординате выраженность ковариаций. Черной линией отмечены ковариации. Серой пунктирной линией отмечены достоверные ковариации (-1 — обратные; 1 — прямые; 0 — отсутствие связи)
Note: A. The black line reflects the performance in units of d', the gray line reflects the amplitude in microvolts (for convenience of display, both graphs are presented in z-coordinates). The x-axis shows the averaged sample window (from 1 to 351), and the y-axis shows the effectiveness and peak amplitude. The gray dotted line marks areas with a reliable inverse relationship, and the black dotted line shows areas with a reliable direct relationship. B. The x-axis shows the average sample window (from 1 to 351). The y-axis shows the severity of the covariances. The black line indicates the covariances. The gray dotted line indicates reliable covariances (-1 — inverse; 1 — direct; 0 — no connection)
Таким образом, анализируя динамику взаимосвязей, можно рассматривать динамику выраженности прямых/обратных взаимосвязей на протяжении эксперимента; связывать это с теми или иными поведенческими маркерами (к примеру — с маркером преодоления точки неслучайного решения (Апанович и др., в печати)), рассматривать процент прямых/обратных/отсутствующих взаимосвязей или анализировать количественную оценку в виде средних значений ковариации на интересующем исследователя диапазоне.
Обсуждение результатов и заключение
В отличие от более традиционных методов анализа временных рядов, предлагаемый нами метод ковариационного анализа с применением «скользящего окна» позволяет оценивать динамику связи временных рядов и их участков, а не только общие показатели связи, сезонность или их сегментацию. Данный метод является дополнением к уже существующим методам обработки временных рядов в том случае, когда анализируемые ряды обладают свойством нестационарности. Это является особенно актуальным в том случае, когда исследуемые процессы обладают нестабильной динамикой, что характеризует большую часть психических феноменов, имеющих процессуальный характер (научение, феномены колебания внимания, утомление, актуализация опыта и т. д.).
Сопоставление методов ковариационного и корреляционного анализов показало, что корреляционный анализ крайне чувствителен к значениям шума, но не учитывает динамику анализируемых показателей. Ковариационный анализ, напротив, устойчив к шуму разной степени интенсивности, что позволяет проводить измерение не только связи временных рядов, но также учитывать динамику анализируемых показателей в том или ином диапазоне. Это дает возможность использовать ковариационный анализ как более информативный по сравнению с корреляционным.
Таким образом, можно говорить о том, что предлагаемый нами метод позволяет делать выводы относительно неравномерного характера связи временных рядов и в дальнейшем сопоставлять разный уровень взаимосвязи с проявлением тех или иных психических феноменов, имеющих процессуальный характер, или поведенческих маркеров, регистрируемых во время проведения эксперимента.
В качестве дальнейшего развития предлагаемого подхода к анализу данных можно предложить применение процедуры сегментации временных рядов (Keogh, Kasetty, 2003). Сегментация позволит выделять гомогенные по своей динамике ряды, к которым возможно применение разработанного нами метода.
В качестве заключения можно говорить о том, что нами был разработан метод оценки связи временных рядов, который позволяет учитывать нестационарность и вытекающий из этого разный уровень связи временных рядов на разных эпохах. Разработанный метод, основанный на ковариационном анализе методом «скользящего окна», позволяет количественно оценивать связь на разных интервалах временных рядов. Данный метод был нами апробирован на смоделированных данных и применен к экспериментальным данным, что позволило интерпретировать нестационарную динамику временных рядов и выделять эпохи, характеризующиеся разной степенью и направленностью связи.
Ограничения. В качестве ограничений метода можно обратить внимание, что при работе со стационарными рядами (например, имеющими выраженную «сезонность») применение описанного нами метода лишено смысла и является переусложненным. Также ограничением является необходимость теоретического обоснования полученной динамики взаимосвязи временных рядов и ее интерпретация, которая может оказаться невозможной в некоторых психологических парадигмах (где принято исследовать не динамику процессов, а диспозиционные индивидуально-психологические характеристики).
Limitations. As limitations of the method, it should be noted that when working with stationary series (for example, those with pronounced “seasonality”), the application of the method we have described is meaningless and overly complicated. Another limitation is the need for theoretical justification of the obtained dynamics of the relationship between time series and its interpretation, which may be impossible in some psychological paradigms (where it is customary to study not the dynamics of processes, but dispositional individual psychological characteristics).