1. INTRODUCTION
Nowadays computer testing is widely used in medicine, psychology and education for diagnostics and estimation of professional skill level for different activities. That includes also important applications in education quality control. Both quality of testing and reliability of its results strongly depend on a selected technology, which became an object of active scientific research last years.
At first tests were developed on the basis of the classical test theory[2,15,18,19] borrowed from physics. This theory assumes that measured characteristics have some “true” values distorted by random and system errors. This approach was quite popular but has a series of significant defects preventing its practical applications:
- The problems appear when comparing similar peculiarities of tested subjects, which are revealed with the aid of different methods
- The validity problem is not solved
- Test points become insufficiently reliable in the ranges of extreme values
- The method itself is insufficiently reliable and universal.
A new testing technology was developed to overcome the stated problems. It is based on the latent-structural analysis[Kuravsky, 2002] and called the Item Response Theory (IRT)[15,17]. The adaptive testing concept is implemented in this theory, according to which a tested subject gets the calculated tasks of certain difficulty that depends on his current skill level estimation at each step of the testing procedure. The main concept of this new theory was proposed by G. Rash in 1960[Rasch]. It assumes that probability of the correct answer for a task is determined by the difference of skill level and test difficulty. Depending on the application problem conditions, practically used are also other models which are more complicated and built on the given concept basis[1,26,28,29].
Application of this technology results in some problems:
- “Static” nature of estimates, viz.: ignoring the essential changes of subject characteristics under study during testing procedure, which may become apparent owing to influence of tiredness and other factors
- Time spent on solving tasks has no influence on skill estimation
- A subject needs to solve rather great number of test tasks to get sufficient accuracy of skill estimation
- Difficulty of calculating probability distributions of possible test results that is necessary for evaluating their reliability
- Procedure of estimating result accuracy, which entails application of both the maximum likelihood method and calculation of confidence intervals and, as a result, is comparatively difficult for practical implementation.
The indicated problems make development of new testing technologies topical. Under consideration in this paper are new aspects of application of the approach to adaptive testing [4-11,20-25], which was developed by the authors before and is based on application of trained structures in the form of discrete- and continuous-time Markov models. Its main features are:
- Revealing and using temporal dynamics of ability to solve test tasks in constructing estimates
- Possibility of taking the time spent on solution of test tasks into account in constructing estimates
- Possibility of studying temporal skill dynamics in both discrete and continuous time scales
- The number of tasks, which should be put to the subjects to obtain estimates of their skills with a given accuracy, are less than in case of other approaches, with the testing process being accelerated
- Obtaining the probability distribution of possible test results as the outcome
- Advanced technique of identifying model parameters.
The indicated facilities provide for advantages of the new approach over currently used similar testing techniques.
One of the most serious problems arising from the testing process is appearance of artifacts in history of subject responses, which distort testing results. These artifacts are conditioned by outer hints, guessing and other forms of illegal purposeful interference in testing procedure. The presented adaptive testing technology makes it possible to fight against these effects, with eliminating artifacts on the basis of comparing observed and expected subject responses for different skill levels. The Kalman filter[14, 16] that is a non-stationary feedback system including a forming filter reproducing the ideal behavior model is suggested here as a tool for such a comparison.
Selection of the Kalman filter for testing artifact elimination is optimal choice since it meets both the accepted adaptive testing concept and relevant context of use better than competitive approaches. In particular, this filter:
- in contrast to the Wiener filter, can process current information on subject response in real time, forming its output after getting next answer immediately without full testing protocol that is not available until completing all the answering procedure
- in contrast to the Stratonovich filter, applies linear estimation methods only, which meet the linear differential adaptive testing model in use best of all and do not complicate the solution process groundlessly
- in contrast to the Luenberger filter, takes into account observation errors and ensures optimal estimation.
Presented in this paper are a new adaptive testing approach based on application of trained structures in the form of continuous-time Markov models, formulation of the artifact Kalman filtration problem and peculiarities of its solution.
2. MARKOV MODELS OF ADAPTIVE TESTING
2.1. Structure and mathematical description of Markov models in use. Procedure of skill level estimation
Estimation of probabilities for various skill levels is performed basing on test results obtained with the aid of parametric mathematical models described by Markov random processes with discrete states and continuous or discrete time[12,13]. Further discussion applies to the models with continuous time only. Directly observable quantity is the difficulty of task being executed, measured in logit. The valid range of this quantity is divided into several intervals, each of them is considered as a separate state xt, i=0, 1 ,...,n, in which a testee may be with certain probability, transferring from one state to another according to certain rules. The length of these intervals determines the discrimination of estimates obtained in the testing process. In turn, the number of states is determined by the desired discrimination of estimates and available sample size[Avanesov, 2003].
Both task difficulties and subject’ skills are measured in a common dimensionless logit scale that represents the ratio of correct and incorrect answers. Conversion to the logit scale is determined by the formula:
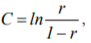
where С is the required value of the logit scale, r is probability of correct task performance. In case of difficulty assessing this parameter describes the possibility of performance of a certain task for the entire set of subjects and in case of measuring skills - the results of a certain subject for the entire set of admissible tasks. Statistical approximations of the given quantities are obtained after replacing probability r by its sample estimates in this formula.
Models which describe the dynamics of these transitions are directed graphs, where nodes[Kardanova] correspond to states and arcs[Cramer, 1976] correspond to transitions.
In case of models with continuous time the testing process can be regarded as a random walk on a graph with transitions from one state to another following the arc’s directions. These transitions are instantaneous and occur at random moments.
It is assumed that they meet the following two properties of Poisson flows of events:
- Ordinary (the flow is called ordinary if the probability for occurrence of two or more events during a short time interval is much less than the probability for occurrence of one event during the same period)
- Independence of the increments (this property means that numbers of events falling into two disjoint intervals are independent on each other).
It can be shown that the number of events X that fall at any time interval of length T, beginning at the time t, is distributed according to the Poisson law in the considered flows:
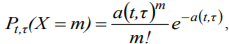
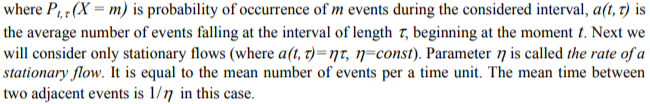
The aforementioned assumptions concerning the nature of event flows are usual for applications as these flows (or flows which close to them) are frequently take place in reality because of limit theorems for events[12,13].
For continuous-time models, unknown (free) model parameters are events’ flow rates. Their values are identified by means of comparing the observed and expected histograms describing the distributions of frequencies for being in the model states, viz.: computed are the rates that provide the best fit for observed and expected frequencies of falling into certain model states at the given time points, in which observed data are available. Expected state probabilities are calculated by integrating the sets of Kolmogorov equations numerically.
Continuous-time Markov models in which free parameters are identified using observation data are called Markov networks[5,7,21-23].
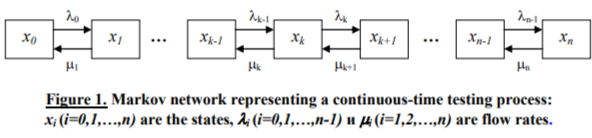
To describe how the probabilities of being at the given states vary with time, Markov networks and chains organized according to the so-called "death and propagation" scheme[Kuravsky, 2002] are applied (Figure 1). This scheme is a finite succession of n+1 states, in which transitions from state 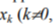
 are possible only to the previous state xk-1 or to the next state xk+1. From states x0 and xn only states x1 and xn-1 are available, correspondingly.
are possible only to the previous state xk-1 or to the next state xk+1. From states x0 and xn only states x1 and xn-1 are available, correspondingly.
Probability dynamics of being in various model states for the given scheme is described by the following set of the Kolmogorov ordinary differential equations:
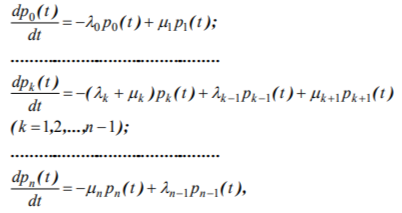

The procedure of adaptive testing for both model types consists in successive presentation of tasks to a subject, with their difficulty being determined by the state of Markov network, where this subject is at the moment. If the subject being in state xi completes the task successfully, he goes into state xi+1, otherwise - into state xi-1. Upon completion of testing procedure the subject finds himself in one of states x*, which meet his skill level best of all. The principle of selecting a next task is to take the test item, whose difficulty meets approximately the current estimation of subject skill. According to the performed studies and modern test theory results, this ensures the best differentiation of subjects in terms of their abilities.
2.2. Identification of continuous-time Markov models
Identifications of Markov models are carried out separately for samples of subjects for each of the considered skill levels. Every skill level 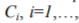 , has its own unique set of model parameters estimates. These sets allow later to identify the skill level that meets observations data best of all. Thus, transition probabilities and flow rates are functions of two characteristics: skill level and task difficulty. Number of skill levels is a discrete parameter, which specifies the estimation discrimination for a given characteristic. It is selected for each application problem according to an available subjects’ sample size and desired result accuracy.
, has its own unique set of model parameters estimates. These sets allow later to identify the skill level that meets observations data best of all. Thus, transition probabilities and flow rates are functions of two characteristics: skill level and task difficulty. Number of skill levels is a discrete parameter, which specifies the estimation discrimination for a given characteristic. It is selected for each application problem according to an available subjects’ sample size and desired result accuracy.
A discrete-state Markov process is attributed to each time-varying histogram of being in model states. The Pearson statistics
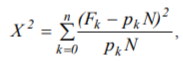
where N is sample size, pk is expected probability of being at the k-th model state, and Fk is observed frequency of being in k-th model state, is used as a goodness-of-fit measure in the sense that its large values correspond to bad fit and its small values correspond to good fit. For model identification, the sum of these statistics is minimized in those time points, at which the observation data are available. Observed numbers of hits at different intervals of task difficulty result from testing. The values yielding the best fit of observed and expected frequencies of falling into certain system states at the given time points are considered as required estimates of free model parameters.
It has been proven that under some common conditions the values of the Pearson statistics 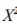 obtained after true solution substitution are asymptotically described by
obtained after true solution substitution are asymptotically described by 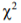 distribution with n-l degrees of freedom, where l is the number of parameters to be determined. Moreover, the calculated values of free parameters converge in probability to the target solution with the increase of sample size [3, pp.462-470]. This allows applying the given statistics for verifying the hypothesis that the obtained forecast fits the observation data. The given way of identifying free model parameters is called the method of X minimum[Cramer, 1976]. It yields solutions which are close to those obtained by the maximum likelihood technique[3, pp.461-462].
distribution with n-l degrees of freedom, where l is the number of parameters to be determined. Moreover, the calculated values of free parameters converge in probability to the target solution with the increase of sample size [3, pp.462-470]. This allows applying the given statistics for verifying the hypothesis that the obtained forecast fits the observation data. The given way of identifying free model parameters is called the method of X minimum[Cramer, 1976]. It yields solutions which are close to those obtained by the maximum likelihood technique[3, pp.461-462].
In case of continuous-time models the employed identification procedure consists of two stages. At the preparatory stage, some numerical integration scheme for the aforementioned differential equations is coded with a spreadsheet to calculate the probability functions pk [5,7,21]. These functions are computed with a given time step. Runge-Kutta methods and their equivalents proved to be sufficient to get acceptable accuracy of solution.
At the final stage, a numerical procedure of multidimensional nonlinear optimization[Kuravsky, 2001] [5,7,21] to get required values of free parameters is run. Obtained estimates are considered as model characteristics revealed by the observations. Also the presented criterion allows to compare different variants of Markov models, selecting the best one.
2.3. Calculation of the optimal solution
Knowing a model state, in which the subject is after solving the last task, and calculating the probability of being in this state at the given time for each of the considered skill levels using differential dependencies (see Section 2.1) one can estimate the probabilities of being in the obtained final state with the aid of the Bayes’ formula:

As shown in Section 2.1, discrimination of the given estimation is determined by the length of the logit interval between the corresponding adjacent skill levels, which, in its turn, results from the number of skill levels I on the assumption of constancy of such intervals.
3. MATHEMATICAL FORMULATION AND SOLUTION OF THE KALMAN FILTRATION PROBLEM IN ADAPTIVE TESTING WITH MARKOV MODELS IN USE

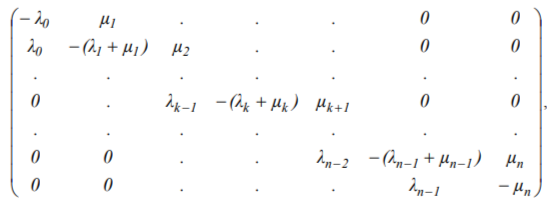

In the classical case this factor is given by the equation



In accordance with the presented adaptive testing procedure, the Kalman filtration is carried out autonomously for each of the skill levels which are taken into account in definition of a problem to be solved.
Finally, it should be noted that there are some interesting analogies between the Kalman filter and hidden Markov models[8, 24], which are partially under consideration in the review[B.D. Wright].
4. SOFTWARE IMPLEMENTATION
The filtration procedure under consideration has been software implemented using the LabVIEW graphical programming software environment (Figure 2), with integration of both the Riccati matrix equation and the Kalman filter equation having been carried out by numerical methods8. To estimate initial state of the error covariance matrix U(0), about which the observations do not yield usually sufficient useful information, the following assumptions were in use:
- E(e(0))=0
- Components of the e(0) vector of filtration errors are statistically independent
- Variances for components of the e(0) vector of filtration errors are proportional to the corresponding variances for components of the observed random noise vector v(t).
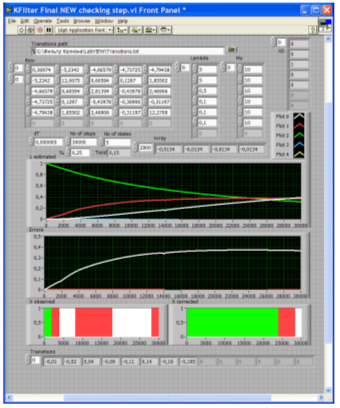
Figure 2. Results of Kalman filtration for the Markov model with 5 states.
5. MAIN RESULTS AND CONCLUSIONS
1. The probabilistic method to filter out artifacts distorted adaptive testing results, which is based on application of trained structures in the form of continuous-time Markov models was developed and software implemented.
2. Elimination of artifacts conditioned by certain forms of illegal purposeful interference in testing procedure is carried out on the basis of comparing observed and expected subject responses for different skill levels with the aid of the Kalman filter adapted to peculiarities of the adaptive testing problem.
3. Selection of the Kalman filter for elimination of artifacts is the optimal approach among the relevant ones since it meets the adaptive testing concept under consideration as well as its application context in the best way.
4. The approach suggested has advantages over the testing techniques, which were used before, owing to its greater information capability, acceleration of a test procedure and firmness with regards to illegal purposeful interference in testing procedure.
[Avanesov, 2003] Considering continuously changing parameter as discrete value we loss a portion of information (it occurs at any idealization). But these losses are insignificant in case of large sample sets when we can set state interval length to be less than measurement error.
[Kardanova] Denoted as rectangles.
[Cramer, 1976] Denoted as arrows.
[Kuravsky, 2002] This scheme was applied firstly in biology to analyze the dynamics of population growth.
[Kuravsky, 2001] A lot of software for numerical optimization is available now. In particular, users of the Excel spreadsheet can apply Frontline Systems, Inc. programs.
[Kuravsky, 2005] Peculiarities of these models are: absence of information noise, equality of dimensions for information and observation processes, unity observation matrix.
[Kuravsky, 2003] Kalman filter output.