Новый подход к построению интеллектуальных и компетентностных тестов^*

1.     ВВЕДЕНИЕ

Компьютерное тестирование в настоящее время широко используется в медицине, психологии и образовании с целью диагностики, определения уровня компетенций и пригодности испытуемых для выполнения тех или иных функций, включая контроль качества обучения. Качество тестирования и достоверность его результатов в значительной степени зависят от технологий проведения тестов, которые в последние десятилетия стали предметом активных научных исследований.

В первое время тесты строились на основе классической теории тестирования [28, 36, 37], в основе которой лежит теория погрешности измерений, заимствованная из физики: полагалось, что измеряемые характеристики имеют некоторые «истинные» значения, искажаемые случайными и систематическими погрешностями. Этот подход получил определённое распространение, однако его практическому применению препятствует ряд существенных недостатков:

-     возникают проблемы при сравнении сходных особенностей испытуемых, выявленных с помощью разных методик;

-        не решается проблема валидности;

-       тестовые баллы становятся недостаточно надёжными в областях экстремальных значений;

-       технология в целом недостаточна надёжна и универсальна.

Для преодоления указанных проблем была разработана новая технология тестирования, основанная на латентно-структурном анализе и до сих пор называемая современной теорией тестирования (IteimRespionseTheiory - IRT) [28, 31, 50]. В русскоязычной литературе также используются и другие варианты её названия: теория ответов на вопросы, стохастическая теория тестов, математическая теория измерений, теория латентных черт, теория характеристических кривых заданий, теория моделирования и параметризации педагогических тестов и т.д. Основная концепция данного подхода, предложенного Г. Рашем в 1960 году, предполагает, что вероятность правильного ответа на задание определяется разностью уровня знаний или способностей и трудности теста. В зависимости от условий прикладной задачи на практике используются и другие, более сложные модели, построенные на базе данной концепции [50, 56, 57].

В рамках технологии IRT может быть реализована концепция адаптивного тестирования, согласно которой испытуемому с определённой текущей расчётной оценкой уровня знаний или способностей на каждом шаге тестирования вычисляются и предлагаются задания со сложностью, обеспечивающей наибольшую дифференциацию результатов для разных категорий испытуемых.

Применение технологии IRT приводит к следующим проблемам:

-     «статичность» оценок: игнорирование того факта, что результат тестирования вследствие усталости испытуемых и других факторов может, вообще говоря, существенно изменяться со временем, принимая различные значения в процессе сеанса тестирования;

-     невозможность учёта времени, затрачиваемого на решение тестовых задач, при построении расчётных оценок;

-     необходимость выполнения достаточно большого числа заданий для получения оценок с приемлемой точностью;

-     сравнительно сложная для практической реализации процедура оценки точности результата, связанная с применением метода максимального правдоподобия и расчётом доверительных интервалов.

Указанные проблемы сделали актуальными поиск и разработку новых принципов построения технологий тестирования. Одним из наиболее перспективных результатов в этой области стал новый подход к адаптивному тестированию [15, 18, 20, 22], построенный на использовании обучаемых структур в форме марковских моделей с дискретным и непрерывным временем. Его особенностями, обеспечивающими преимущества перед аналогичными способами тестирования, являются:

-     выявление и использование при построении расчётных оценок временной динамики изменения способности справляться с заданиями теста;

-     возможность учёта при построении расчётных оценок времени, затрачиваемого на решение тестовых задач;

-     возможность исследования временной динамики знаний или способностей как в дискретной, так и в непрерывной временной шкале;

-     меньшее по сравнению с другими подходами число заданий, которое следует предъявлять испытуемому для получения оценок знаний или способностей с заданной точностью, что ускоряет процесс тестирования;

-     получение распределения вероятностей возможных результатов теста в качестве конечного результата;

-            развитая техника идентификации параметров моделей.

Одной из наиболее серьёзных проблем, возникающих в процессе тестирования, является проявление в истории ответов испытуемого влияния искажающих результаты артефактов, обусловленных подсказками, угадыванием и другими формами некорректного целенаправленного вмешательства в процедуру испытаний. Разработанная технология адаптивного тестирования на базе марковских моделей позволяет бороться с этим явлением, устраняя артефакты на основе сравнения наблюдаемых и прогнозируемых результатов ответов на вопросы для разных уровней способностей испытуемых [21, 24]. В качестве инструмента для сравнения используется приспособленный для решения задачи тестирования многомерный непрерывный фильтр Калмана [27, 30] - нестационарная система с обратной связью, включающая в себя как составную часть формирующий фильтр, воспроизводящий идеализированную модель поведения.

Второе перспективное направление в развитии технологий тестирования связано с применением факторных моделей [26]. Его преимуществами по сравнению с другими подходами является отсутствие проблемы оценки сложности заданий тестов, а также возможность описания структуры способностей методами структурного моделирования. Устранение артефактов тестирования в этом случае обеспечивается многомерным цифровым фильтром Калмана. Процедура тестирования является неадаптивной. Этот подход, как и предыдущий, учитывает влияние фактора времени на результаты тестирования и обеспечивает уменьшение времени прохождения процедуры испытаний.

На основе рассмотренных выше технологий тестирования, использующих марковские и факторные модели, разработаны системы поддержки принятия решений [18, 26], которые ускоряют процесс тестирования, оптимизируя предъявление тестовых заданий. Диагностические выводы строятся на основе уточняющихся в процессе тестирования вероятностных оценок принадлежности испытуемых к различным категориям. Подобные инструменты дают практикующему специалисту дополнительную информацию для анализа и, в случае марковских моделей, предоставляют рекомендации по выбору следующего теста, обладающего, по сравнению с прочими, наибольшей для данного испытуемого дифференцирующей способностью. Такие рекомендации, не являясь обязательными и не лишая специалиста возможности получения собственного опыта, направляют его по наиболее эффективному и надёжному пути. Следует отметить, что сам процесс тестирования при этом не становится полностью автоматическим в силу многокомпонентности процедуры оценки способностей и наличия дополнительных неформализуемых критериев.

Все рассмотренные выше технологии тестирования объединяет общий признак: итоговые оценки обычно определяются только по формальным результатам выполнения заданий, предъявляемых испытуемому, без анализа хода его рассуждений и динамики изменения состояния человека в процессе выполнения теста. Это существенно ограничивает возможности измерительной процедуры, что обусловлено, во-первых, её, как правило, значительной продолжительностью, изменяющей психофизиологическое состояние испытуемого и его способности справляться с заданиями, и, во-вторых, упомянутой выше проблемой некорректного целенаправленного вмешательства в процедуру испытаний, искажающего вычисляемые баллы.

Перспективы преодоления этих проблем, по мнению многих экспертов, связаны с включением в процесс тестирования методов современной экспериментальной психологии и, в частности, средств анализа глазодвигательной активности [1-7]. Среди разработанных в этой области общих подходов следует отметить:

-     анализ традиционных параметров траекторий движений глаз (общего времени чтения, усреднённых характеристик фиксаций, прогрессивных и регрессивных саккад и т.д.) [8, 51],

-     анализ специальных показателей траекторий (соотношений времен пребывания взора в различных зонах стимула, частот посещений различных зон стимула и переходов от одной зоны к другой, степени следования испытуемыми различным пространственным стратегиям и т.д.) [25, 29, 47, 55],

-                       анализ символьных последовательностей с использованием метрики различий [32, 46],

-     методы, основанные на исследовании структуры и различных манипуляциях с матрицами переходных вероятностей цепей Маркова [34, 35, 38, 39, 48, 52, 53],

-                       методы, построенные на использовании скрытых марковских моделей [33, 49, 52, 53, 54].

Наиболее перспективными для анализа глазодвигательной активности испытуемых при прохождении тестовых процедур представляются так называемые матрицы представления преемника (SR-матрицы), вычисляемые как пределы сумм степенных последовательностей матриц переходных вероятностей цепей Маркова [34, 38].

Несмотря на отдельные примеры практического применения, развитие и распространение перечисленных выше методов, включая анализ SR-матриц, сдерживается рядом ограничений, наиболее существенными из которых являются слабые возможности для исследования временной динамики движения глаз, неразвитый математический аппарат, низкая степень дифференциации проблемных категорий испытуемых и недостаточная универсальность.

В этой работе предложен новый подход к построению интеллектуальных и компетент- ностных тестов[19], основанный на представлении движения взора испытуемого по поверхности стимулов с помощью одной из наиболее общих разновидностей случайных процессов и технологиях его последующего анализа. Особое внимание уделено математическому обоснованию рассмотренных методов. В качестве иллюстрации приведён пример практического применения полученных результатов для выявления уровня математической подготовки студентов и школьников.

2.     МАТЕМАТИЧЕСКИЕ АСПЕКТЫ НОВОГО ПОДХОДА К ПОСТРОЕНИЮ ТЕСТОВ

Будем полагать, что испытуемым предъявляется плоский стимул прямоугольной формы, представляющий содержательную информацию по определённой тематике. Испытуемые разделены на несколько заранее известных категорий, отражающих уровень знаний или компетенций по данной тематике. Считая, что для каждой из этих категорий имеется идентифицированная по результатам наблюдений оценка распределения вероятностей пребывания взора на поверхности стимула, поставим задачу распознавания категории ® £ Q, к которой принадлежит испытуемый, по данным о движении его взора по поверхности стимула.

Классификация в указанной постановке обеспечивается решением рассмотренных далее следующих подзадач:

-     выбора математического представления движения взора испытуемого по поверхности стимула;

-     идентификации распределения вероятностей пребывания взора на поверхности стимула по результатам наблюдений для всех рассматриваемых категорий испытуемых;

-     оценки вероятности наблюдаемой траектории движения взора по поверхности стимула при условии принадлежности к каждой из заданных категорий испытуемых.

Для вычисления приближённого решения приведённого выше уравнения Фокке- ра-Планка-Колмогорова проведём дискретизацию замкнутой области стимула 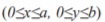 прямоугольной сеткой, равномерной вдоль каждой из осей (рис. 1).

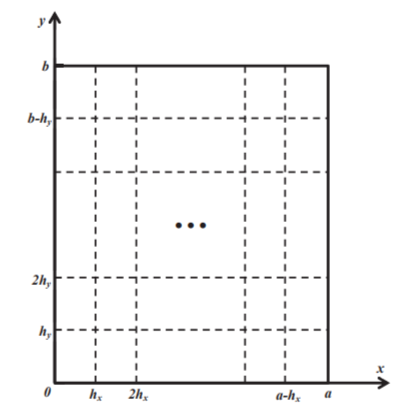
Рис. 1. Дискретизация замкнутой области стимула прямоугольной сеткой.

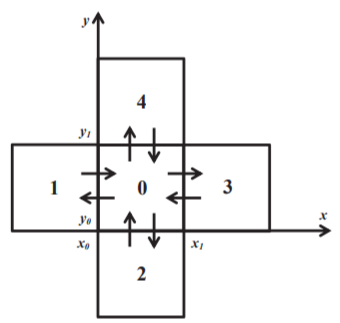
Рис. 2. Произвольная внутренняя ячейка прямоугольной сетки.

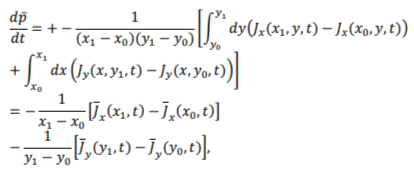
Уравнения для граничных ячеек сетки получаются путём удаления из данного уравнения слагаемых, относящихся к отсутствующим элементам.

Процедура вычисления оценок свободных параметров состоит из двух этапов. На подготовительном этапе с помощью электронной таблицы для рассматриваемой системы обыкновенных дифференциальных уравнений кодируется численная схем нтегрирования, позволяющая вычислять вероятностные функции 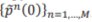 [12, 13, 16, 40, 41, 42] с некоторым заданным временным шагом. Для вычисления решений с приемлемой точностью оказались достаточными методы Рунге-Кутта или их эквиваленты. Дл решения задачи важно, что электронная таблица поддерживает динамические связи мжду со ржимым ячеек. Ели пом- стить свободные параметры и временной шаг в отдельные ячейки, на которые ссылаются как ячейки, содержащие формулы для вычисления производных в системе дифференциальных уравнений, так и начальные вероятности нахождения в различных состояниях сстемы, то все рше- ние будет автоматически модифицироваться по мере изменения значений свободных параметров.

На заключительном этапе запускается численная процедура многомерной нелинейной оптимизации [12, 13, 16, 40, 41, 42]. Значения параметров, полученные с её помощью, рассматриваются как характеристики математической модели, выявленные в результате наблюдений. Следует отметить, что рассмотренная процедура обеспечивает решение обратной задачи, при котором вычисляются параметры системы дифференциальных уравнений, определяющей решение с заданными характеристиками.

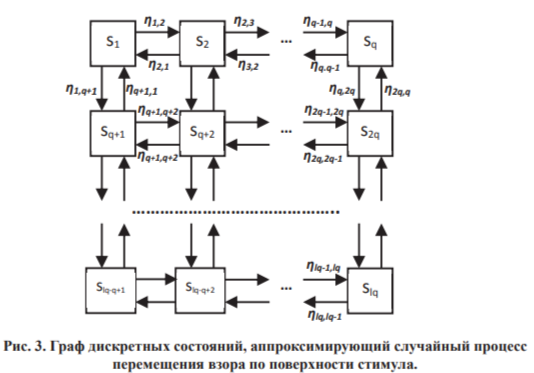
Как правило, идентификация свободных параметров случайных процессов со структурой связей между состояниями, представленной на рис. 3, является сложной вычислительной задачей. Однако имеется эффективный приём, позволяющийупростить эту работу.

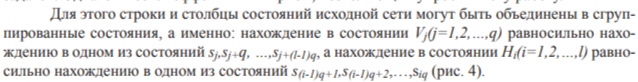
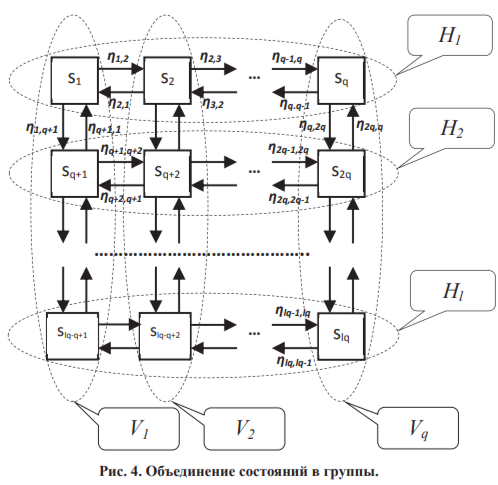
Получаемые при этом графы состояний представлены на рис.5 и 6.

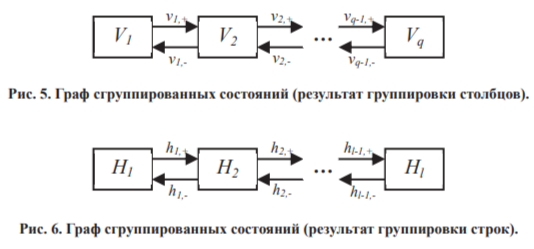
Поскольку вероятность пребывания в каждом из сгруппированных состояний равна сумме вероятностей пебывания в составляющих его состояниях исходного случайного процесса, уравнения Колмогорова для вероятностей нахождения взора в сгруппированных состояниях получаются путём согласованного суммирования левых и правых частей всех уравнений (4), которые соответствуют ячейкам, формирующим данные состояния:

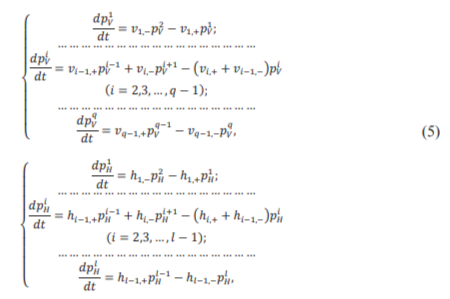
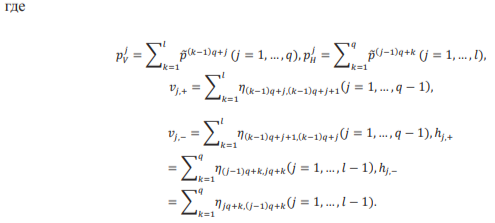
На практике приведённые выше интегралы для вычисления Р_го заменяются своими численными оценками.

3.     ПРИМЕР ПРАКТИЧЕСКОГО ПРИМЕНЕНИЯ

3.1.     Экспериментальная процедура и оборудование

Рис. 7. Регистрация движений глаз испытуемого с помощью системы SMI HighSpeed.

В эксперименте приняли участие 24 студента и школьника, имеющие нормально или скорректированное до нормального зрение.

Стимульный материал первого задания представлен на рис. 8. Заданный текст содержит контрольную ошибку: в предпоследнем предложении нельзя производить разложение множителя x²+1 на составляющие с вещественными коэффициентами.

Рис. 8. Стимульный материал первого задания, в котором описано решение
задачи на разложение полинома на множители.

Рис. 9. Стимульный материал второго задания, в котором описано решение
алгебраической проблемы собственных значений.

3.2.     Аппроксимация решения и результаты диагностики

Область, на которой располагается стимульный материал, была разбита прямоугольной сеткой размерностью 4x4 на 16 ячеек, что обеспечило высоту строк и ширину столбцов равными, соответственно, 256 и 320 точкам (см. рис. 10).

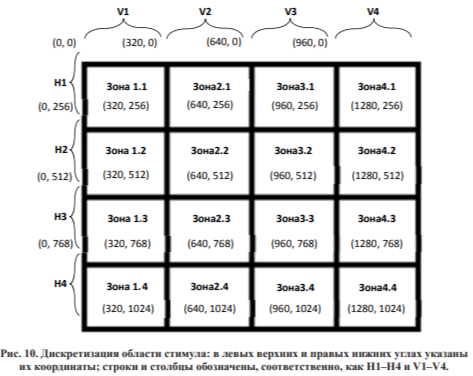
Для обеспечения лучшего соответствия результатов моделирования наблюдениям, интенсивности переходов между состояниями исследуем ого случайного процесса идентифицировалась по отдельности для следующих друг за другом временных интервалов длительностью 10 секунд. Для решения задачи оптимизации использовалось программное обеспечение компании FrontlineSystems, реализующее метод обобщенного градиентного спуска.

Численное интегрирование систем уравнений Ко мгорова с идентфицирован- ными значениями указанных параметров позволило вычислить погнозируемы вероятности пребывания в сгруппированных состояниях. Зависимости этих вероятностей от времени для второго задания совместно с соответствующими оценками, полученным в результате наблюденй, в качестве иллюстрации прив дены на рис. 11-14. Как видно из графиков, идентификаця свободных параметров моделй приводит к определённому сглаживанию наблюдаемых данных, устраняющему их лучайную «шумовую» составляющую.

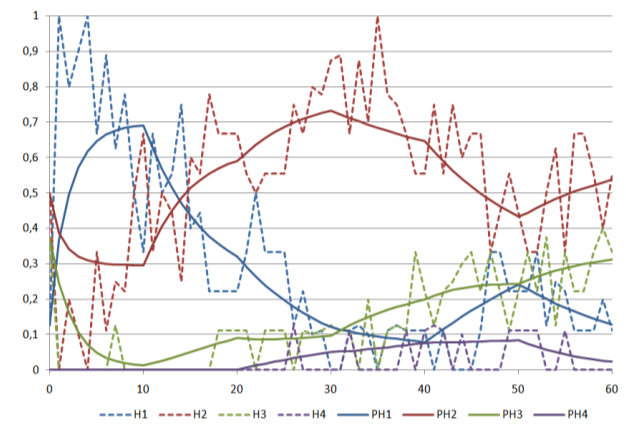
Рис. 11. Зависимости от времени (в секундах) прогнозир емых вероятностей пребывания в состояниях, сгруппированных по строкам, и соответствующих им оценок, полученных в результате наблюдений, для испытуемых, выполнивших второе задание: H1-H4 - наблюдаемые оценки (показаны пунктиром), PH1-PH4 - прогнозируемые оценки.

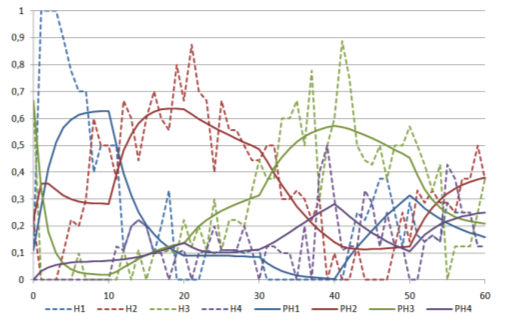
Рис. 12. Зависимости от времени (в секундах) рогнзируемых верояностей пребывания в сост яниях, сгруппированных по строкам, и соответ твующих им оценок, полученных в результате наблюдений, для испытуемых, не выполнивших второе задание: H1-H4 - наблюдаемые оценки (показаны пунктиром), PH1-PH4 - прогнозируемые оценки.

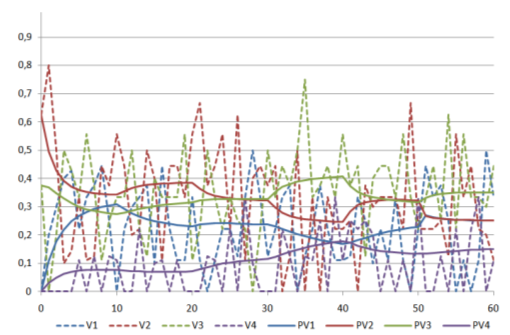
Рис. 13. Зависимости от времени (в секундах) прогнозируемых вероятностей пребывания в состояниях, сгруппированных по столбцам, и соответствующих им оценок, полученных в результате наблюдений, для испыту мых, выполнивших вт рое задание: V1-V4 - наблюдаемые оценки(показаны пунктиром), PV1-PV4 - прогнозируемые оценки.

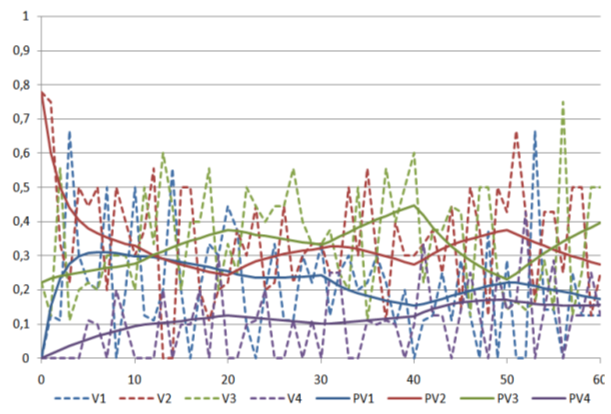
Рис. 14. Зависимости от времени (в секундах) прогнозируемых вероятностей пребывания в состояниях, сгруппированных по столбцам, и соответствующих им оценок,полученных в результате наблюдений, для испытуемых, не выполнивших второе задание: V1-V4 - наблюдаемые оценки (показаны пунктиром), PV1-PV4- прогнозируемые оценки.

4.     ОСНОВНЫЕ РЕЗУЛЬТАТЫ И ВЫВОДЫ

1.    Перспективы разработки современных технологий тестирования связаны с включением в измерительный процесс методов современной экспериментальной психологии и, в частности, средств анализа глазодвигательной активности.

2.    Развитие и распространение имеющихся достижений в этой области сдерживается рядом ограничений, наиболее существенными из которых являются слабые возможности для исследования временной динамики движения глаз и неразвитый математический аппарат.

3.    Разработан новый подход к построению интеллектуальных и компетентностных тестов, основанный на представлении движения взора испытуемого по поверхности стимулов с помощью марковского случайного процесса, распределение переходных вероятностей которого удовлетворяет уравнению Фоккера-Планка-Колмогорова, и диагностической процедуре, которая обеспечивается идентификацией распределения вероятностей пребывания взора по поверхности стимула по результатам наблюдений для всех рассматриваемых категорий испытуемых и оценкой вероятности наблюдаемой траектории движения взора при условии принадлежности к каждой из заданных категорий испытуемых.

4.    Разработан метод приближённого решения уравнения Фоккера-Планка-Колмогорова, сводящий исходную задачу к решению задачи Коши для системы обыкновенных дифференциальных уравнений Колмогорова относительно плотностей вероятности пребывания взора на поверхности стимула, усреднённых по площади ячеек его дискретизованной области.

5.    Разработан метод идентификации интенсивностей переходов между ячейками дискретизо­ванной области, входящих в качестве свободных параметров в систему дифференциальных уравнений Колмогорова. Этот метод обеспечивает построение приближений к оценкам максимального правдоподобия и опирается на численную процедуру многомерной нелинейной оптимизации, что обеспечивает решение обратной задачи для указанной системы уравнений.

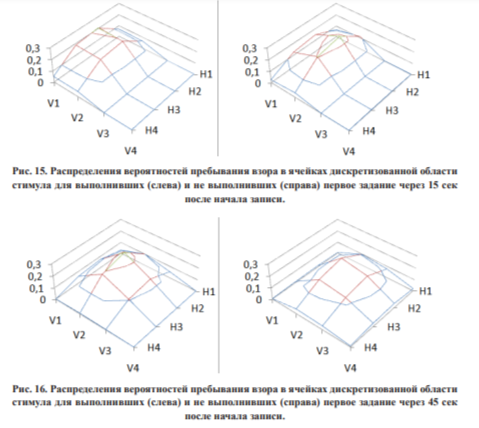
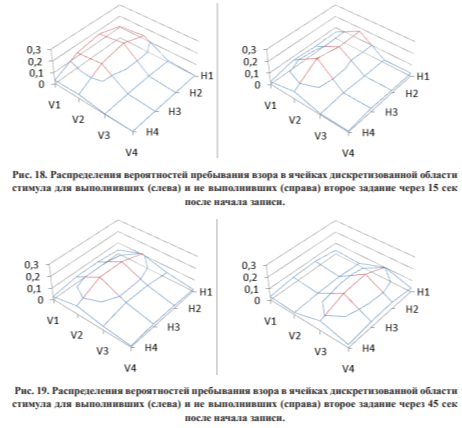
6.    Предложен статистический критерий для оценки степени соответствия наблюдаемых и прогнозируемых частот пребывания в ячейках дискретизованной области стимула в контрольные моменты времени, построенный на основе анализа регрессионной зависимости этих частот.

7.    Приведённый в данной работе пример практического применения полученных результатов для выявления уровня математической подготовки студентов и школьников свидетельствует об эффективности предложенного подхода к построению процедур тестирования.