Модель сопредставленности для оценки вероятности объединения событий

Принятие людьми эвристических решений часто оценивается с помощью ставших привычными научных представлений, которые могут ошибочно использоваться в качестве норм и критериев ис¬тинности при оценке психологии человека. В частности, представление об «ошибке объединения», связанное с нарушением людьми правила объединения вероятности случайных событий можно опре¬делить как форму научной иллюзии. Подход трансцендентальной психологии дает возможность обосновать вероятностную модель сопредставленности событий, которая соответствует психологии восприятия человека и принятию им эвристических решений в ситуации неопределенности

 

1.       ВВЕДЕНИЕ

В современном мире выработанные науками представления играют существенную роль в социальной и производственной жизни и в целом в организации жизнедеятельности людей в обществе. Научные знания и модели имеют большое значение в межкультурной коммуникации, образовании и формировании его стандартов. Они, фактически, часто воплощают универсальные межкультурные истины, которые позволяют создавать всем понятные объяснительные концепции, интегрировать на этой основе социум, предсказывать результаты экспериментов и явлений, осуществлять сравнительные исследования и т.п.

Соотнесение с нормой как общий научный метод заключается в установлении объективной нормы и соотнесении этой нормы с множеством рассматриваемых явлений. В частности, в психодиагностике для определения того, в какой степени у испытуемого развита диагностируемая характеристика, осуществляется сравнение данных испытуемого с показателями других людей и выраженностью других индивидуальных качеств у данного испытуемого. Это позволяет определить положение испытуемого относительно нормативной выборки или выборки стандартизации. Стандартизация психодиагностической методики осуществляется путем проведения этой методики на большой репрезентативной выборке того типа, для которого она предназначена. Определяется средний уровень полученного по выборке показателя, а также мера того, насколько выше или ниже этого уровня оказался результат конкретного испытуемого. Такое тестирование называется нормо-соотнесенным и является наиболее распространенным методом психологической диагностики.

В наиболее общей операционной форме нормативные знания выражаются в математике. Математическое знание обладает при этом универсальностью и часто может быть применено в самых разных науках и областях практики. В этой связи математические модели, широко используемые в обучении, в научном отношении в еще большей степени являются нормативными. Например, модель объединения вероятностей, которая используется для выработки вероятностных суждений о явлениях действительности, по сути, стала являться некоей нормой для оценки вероятностей многих событий, которые обладают той или иной степенью неопределенности их появления.

Вместе с тем принятие эвристических решений в условиях по-разному представленной неопределенной реальности в целом не соответствует модели теории вероятностей [1]. В частности, психология принятия эвристических решений явно не укладывается в стандартную модель объединения вероятностей независимых случайных событий, т.е. по идее это значит, что данная модель не может использоваться в качестве безусловно нормативной модели для оценки правильности психологии поведения человека в условиях неопределенности.

Однако математические модели теории вероятностей очень часто используются в качестве универсальных нормативных моделей в том числе в образовательных практиках самых разных культур. При этом «образование становится одним из самых консервативных элементов культуры, сохраняя те нормы и правила, которые в рамках других институтов уже начали трансформироваться» [2]. В этой связи выявление тех консервативных элементов образования и научного дискурса, которые препятствуют развитию соответствующих сфер культуры и науки является весьма актуальным.

В работе рассматривается практическая применимость математической модели объединения вероятностей случайных событий, как нормативной научной модели для оценки правильности принятия человеком эвристических решений в условиях неопределенности, и предлагается использовать в качестве нормативной - модель определения вероятностей сопредставленных событий, которая в большей мере соответствует психологии восприятия человека.

2.        ЭВРИСТИКИ И МОДЕЛЬ ОБЪЕДИНЕНИЯ ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ СОБЫТИЙ

Амос Тверски и Дэниэл Канеман определили эвристики как типичные приемы образования суждений о событиях в условиях недостаточной или неопределенной информации [3] и выделили два вида часто используемых эвристик - представительности (репрезентативности) и доступности. Эвристики представляют собой интуитивный процесс, заключающийся, в частности, в том, что человек склонен считать более вероятными те случайные события, которые в большей мере соответствуют его личному опыту, стереотипам. Об этих событиях можно сказать, что они репрезентативны или доступны опыту данного человека.

Эвристики в целом представляют собой интуитивные правила или принципы, которые дают возможность людям делать значимые заключения быстро и с меньшими усилиями. Это когнитивные сокращенные пути, ментальные аксиомы, стереотипы и убеждения, оценки на глазок и др. Таким образом, по Канеману и Тверски для того, чтобы делать заключения люди опираются на эвристики, эвристики упрощают процесс выведения умозаключений, эвристики приводят к ошибочному мышлению. При этом, конечно, эвристики необязательно и не всегда приводят к ошибочным выводам. Кроме того, в большинстве случаев люди без эври­стик просто не могут обойтись, поскольку им часто приходится делать выводы при отсутствии нужной информации и времени для логически выстроенного, систематизированного рассуждения, а ситуация требует быстрых решений. Поэтому умозаключения, достигнутые индуктивным путем или на основе интуиции, в этих обстоятельствах являются единственно доступными методам осмысления проблемы.

Эвристика доступности вступает в действие, когда люди основывают свои суждения на наличии информации в памяти и обозначает интуитивный процесс, в котором человек оценивает частоту или возможность события по легкости, с которой примеры или случаи приходят ему на ум, т. е. легче вспоминаются. Ясно, что реальная частота событий совсем не обязательно соотносится с легкостью работы памяти.

Репрезентативной эвристикой называется умение судить о том, насколько хорошо определенные явления представляют собой прототипы. В частности, эвристика репрезентативности состоит в том, что вероятности случайных событий, которые должны произойти, оцениваются в связи с теми событиями, которые уже были явлены или представлены в предшествующем опыте человека.

К репрезентативной эвристике относится также категоризация, производимая на основе сходства между конкретным случаем (реализацией) и членами категории. Если конкретный пример имеет одинаковые свойства с другими членами, то вполне вероятно, что все они относятся к одной категории. Однако это не всегда так, поскольку сходство по свойству или ряду свойств не гарантирует принадлежность к классу, который определяется и рядом других неучтенных в данном случае свойств. Поэтому доверие только сходству по свойствам будет часто приводить к неверным категоризациям.

Показательным примером ошибочной категоризации является так называемая ошибка объединения в оценке вероятностей [4]. Канеман и Тверски предъявляли испытуемым описание следующей ситуации.

Линда, возраст 31 год, одинокая, искренняя и привлекательная. Специализировалась в философии. Когда была студенткой, была очень обеспокоена вопросами дискриминации и социальной справедливости, а также участвовала в антиядерных демонстрациях.

Далее они просили определить - какая из следующих альтернатив более вероятна?

A)    Линда - банковская служащая.

B)     Линда - банковская служащая и активно участвует в феминистском движении.

Большинство людей выбирают вариант B и, по мнению авторов, становятся «жертвами ошибки объединения». Теоретически, для двух случайных событий не может быть, чтобы они вместе были более вероятны, чем каждое из событий в отдельности.

Таким образом, «ошибка объединения», по мнению Канемана и Тверски, это ложная вера, что два события имеют большую вероятность взаимного осуществления, чем каждое из событий в отдельности. Это явление часто представляется в разных работах, как когнитивная иллюзия, и было продемонстрировано авторами в большом наборе разных контекстов, включая: оценку частоты встречаемости слов, личностные суждения, медицинские прогнозы, принятие решений в условиях рисков, подозрения в совершении преступлений и политические прогнозы [5].

«Ошибка объединения» нарушает один из основных качественных законов вероятности - правило объединения вероятностей (независимых) событий. Вероятность объединения P(A&B) не может превысить вероятность составных частей этого объединения P(A) и P(B), поскольку множество возможных событий объединения включено в состав множества составляющих.

Многочисленные психологические исследования показали, что тенденция, связанная с нарушением в практике эвристических решений правила объединения вероятностей случайных событий, носит систематический характер. Причины, почему столь неадекватное поведение имеет место и столь часто встречается, оказываются в целом далеко неясными и слабо объяснимыми. Это вызвало у исследователей естественные вопросы. Почему люди столь часто не могут воспользоваться или пренебрегают логичной научной формой сравнения вероятностей событий [6]? Почему они столь не расположены координировать оценку вероятности ситуации с ее логичной структурной моделью[7]?.

В целом было предложено несколько решений проблемы, связанной с «ошибкой объединения». Тверски и Каннеман объясняли иллюзорное поведение с помощью эвристик репрезентативности и доступности и, в целом, с помощью так называемых «поверхностных» эвристик. В соответствии с эвристическим правилом объединения само объединение может быть более репрезентативным, чем одна из его составляющих, и случаи более специфической категории можно легче вообразить, чем случаи более широкой категории. Поэтому эвристики репрезентативности и доступности могут сделать объединение более вероятным, чем одна из его составляющих.

Эти эвристики много критиковали за то, что они слишком неясны для того, чтобы считаться объяснениями. В частности, было отмечено, что понятие вероятности обладает существенной многозначностью, а в представлениях об объединении категорий имеется очень много неопределенности [7]. Были также разработаны специальные вероятностные модели, объясняющие ошибочное поведение, например, так называемая «теория намеков» [8].

При исследовании эвристик «поверхностных» решений во многих работах интуитивные выводы и оценки вероятности сравнивались со специфическими фиксированными научными результатами - правилами статистики и законами вероятности. Однако есть все основания считать, что эти статистики ошибочно использовать в качестве объективных мер перцептивных и когнитивных процессов. В этой связи, так называемая «ошибка объединения» вполне возможно не является собственно ошибкой человеческого суждения или оценки. Скорее ее можно считать ошибкой ученых, которые ошибочно сравнивают способ оценки вероятностей, по сути, психологически зависимых событий с определенной стандартной нормой, со способом оценки вероятностей независимых событий в традиционной теории вероятностей (т.е. со способом, который был создан для оценки шансов в принципиально другой области реальности).

Ясно, что принятие человеком решений в условиях неопределенности является достаточно сложным процессом, часто основанным на быстром восприятии и осознании большого количества факторов. А также на весьма тонком взвешивании разных ситуативных связей и отношений. В этом смысле поведение профессионала здесь может сильно отличаться от поведения новичка, а абстрактные тестовые ситуации не могут являться единственным мерилом поведения. Эксперименты также показывают, что те люди, кто хорошо познакомились с теорией вероятности и держат в голове ее постулаты, с достаточной легкостью не совершают «ошибки объединения» (интересным также является также то, насколько «завораживающим» эффектом обладает абстрактная простота этой модели знаний, т.е. знания трудно приобрести, но еще труднее отказаться от них).

Таким образом, использование упрощенных моделей и норм для оценки правильности или ошибочности поведения вряд ли можно считать правомерным. Описанную «ошибку объединения», на наш взгляд, неправильно называть ошибкой испытуемого. Скорее ее следует рассматривать как ошибку исследователя - ошибку нормирования поведения человека к упрощенной вероятностной модели реальности случайных событий. То есть, «ошибка объединения», как ошибка испытуемого - иллюзорна.

Это означает, что наблюдаемая «ошибка объединения» может быть представлена как научная иллюзия, которая основана на неверном изначальном предположении об универсальной применимости правил классической теории вероятностей безотносительно к особенностям реальных обстоятельств, которые теряются в абстрактной красоте и универсальной простоте применимости данной модели к рассмотрению случайных явлений.

Основная концепция иллюзии предполагает, что она возникает при наличии существенного различия и разделения между реальным поведением и нормативной способностью (рациональным вычислением). В частности, исследователи рассматривают классические модели рационального поведения в качестве норм, по отношению к которым может быть оценено мышление человека. Если они не соответствуют друг другу, то, как правило, делается заключение, что какое-то нарушение есть в мышлении, а не в нормах [9], поскольку именно выработка этих норм является содержанием науки и сомнение в них в определенной степени равносильно самоотрицанию и потере осмысленности всей проводимой учеными работы.

Другой взгляд на «ошибку объединения» вместе с тем не исключает необходимости более полного объяснения поведения человека в вероятностных условиях и понимания природы процессов, определяющих это поведение. Эвристики, относящиеся к рассмотренной выше «проблеме Линды», рассматривались также на предмет использования испытуемым других возможных моделей, относящихся к предположительной реальности происходящих в этой ситуации психологических процессов [5].

В частности, эвристики репрезентативности и доступности, используемые для объяснения «проблемы Линды» [4], можно связать с оценкой правдоподобности событий и тем насколько хорошо предсказания укладываются в общую модель предполагаемой реальности [10, 11]. Люди в экспериментальной ситуации неопределенности ориентируются на значения ситуаций, определяемых в заданиях, и производят оценку вероятности на основе осмысления ситуации и построения возможной причинно-следственной модели гипотетических событий. Это осмысление во многом происходит на основе возможностей восприятия [12, 13] и его когнитивных и «логических» средств, связанных с полифункциональностью процессов непосредственно-чувственного восприятия. Естественно, что этот способ оценки не может находиться в большом согласии с математической моделью теории вероятностей, разработанной для совершенно иной области реальности.

3.        СОПРЕДСТАВЛЕННОСТЬ СВОЙСТВ ОБЪЕКТОВ ВОСПРИЯТИЯ

С целью прояснения природы механизмов принятия человеком решений в условиях неопределенности обратимся к известным характеристикам психических возможностей человека. Ясно, что они в целом явно отличаются в сторону большей сложности от тех упрощенных формальных или математических моделей и представлений, которыми располагает современная наука. Психологические исследования показывают, что способности человека, основанные на сенсорных, когнитивных, моторных и др. процессах имеют множественную и сложную совокупную природу, являются чрезвычайно чувствительными к контексту, высоко динамичны в своей основе, включают развитую иерархию образования отношений и другие особые свойства и характеристики.

В частности, известно, что процессы восприятия имеют полифункциональный характер с со-существованием различных альтернатив, дающих возможность проводить сравнения между ними. Эти процессы обладают функциональной гибкостью, необходимой для эффективного действия перцептивных и когнитивных систем в постоянно изменяющихся условиях [14]. Они естественно подразумевают особенности и возможности, существенно отличающиеся от последовательности процессов рационального мышления. Понятно, что это не учитывается и не может учитываться в упрощенных абстрактных научных моделях, например, в модели наблюдения равновероятностного континуума.

Обращение к свойствам чувственных образов восприятия показывает, что в непосредственно-чувственном процессе свойства объектов и отношений между ними воспринимаются не только как отдельно выделенные свойства, но и как со-существующие свойства и отношения, с учетом возможности ощущения их изменения и без выделения отдельно каждого их них. Таким образом, свойства и отношения объектов в восприятии являются сопредстав- ленными [15]. В результате с точки зрения реальности восприятия, абстрактный объект с отсутствием или только малым количеством свойств является намного менее вероятным, чем объект со многими одновременно присутствующими и взаимно соотнесенными (сопредстав- ленными) свойствами. В этой связи учет принципа сопредставленности важен при проведении исследований и объяснении различных психических процессов [15].

О механизмах процессов восприятия науке в целом известно относительно мало и существует достаточно много различных взглядов на природу этих процессов. Трасценден- тальная психология восприятия [12, 13, 16] полагает, что свойства образов восприятия являются сопредставленными, поскольку они совместно образуются в общем порождающем их процессе и вместе с тем связаны общей моделью их познания (включая, сохранение и извлечение их из памяти). Важно таким образом иметь в виду, что события, сопредставленные в восприятии, имеют общее происхождение. При этом сама эта общность определяется еще и тем, что представление и представленное в нем отнесены к представляющему Я человека. Отсюда в философском осмыслении сопредставленность связана с особой конституцией процесса представления, как общим способом представления вещей. Сопредставленность выражает «сущностную принадлежность представляющего к конституции представления» [17].

В целом можно утверждать, что процессы восприятия имеют порождающий характер, иерархическое строение и сложную структурно-процессуальную и каузальную организацию, которая так или иначе связана с памятью и знаниями о природе вещей. Все это предполагает, что психологическая природа и механизмы познания и антиципации реальных явлений, скорее всего, являются принципиально отличными от вероятностной логики, выработанной наукой для представления более простых явлений. Соответствующая психологии человека модель по идее должна учитывать то, что согласно данности восприятия реальных объектов для любого из них более достоверным является наличие многих определенных и взаимно соотнесенных свойств, нежели появления (согласно классической модели теории вероятностей) ряда независимых случайных событий.

4.       МОДЕЛЬ СОПРЕДСТАВЛЕННЫХ СОБЫТИЙ

Стандартная модель подсчета шансов в теории вероятностей строится на идее объективного подхода к действительности и на исследовании результатов событий, которые в рамках некоторой гипотетической модели позволяют в целом с нуля получить некоторую информацию о явлении. Фактически каждое событие является актом некоторого измерения и предполагается, что до этого измерения об объекте известны только самые общие вещи, относящиеся к возможности появления события, его зависимости или независимости от других подобных событий. Возможны также дополнительные сведения, например, об одновременности событий, но основная модель соответствует тому, что события и их операционные характеристики появляются в контексте отрицательного (по сути нулевого) знания о предмете практики, т.е. отсутствия предварительного положительного знания об этом предмете (кроме собственно исходной процессуальной модели). С этим, видимо, ранее и была связана одна из основных психологических проблем теории вероятности - как можно считать шансы того, чего пока не существует [18].

Подсчет шансов двух событий A и B, которые являются независимыми, осуществляется весьма просто. Вероятность того, что, например, событие A произойдет, соответствуют Ц и определяется как отношение двух благоприятных для него вариантов, к общему количеству четырех возможных комбинаций истинности событий. Вероятность того, что два события произойдут одновременно, соответствует произведению вероятностей событий A и B и равна 1/4 (один шанс из четырех общих возможностей).

В этой стандартной модели на вопрос: «Что более вероятно A или A&B?» следует однозначный ответ: A более вероятно. Более того в обычном случае бросания одной монеты, когда событиями являются получение «орла» А или «решки» В, случаи одновременности А&В отвечают невозможным зависимым событиям и вопрос: что более вероятно A или A&B получает еще более простое решение, поскольку вероятность невозможного события автоматически полагается равной нулю.

Эти расчеты соответствуют модели теории вероятностей, которая стала стандартной для правильной оценки вероятностей самых разных явлений. Не подвергая сомнению само правило расчета вероятностей, можно, однако, подвергнуть сомнению применимость данной модели для представления человеческого (психологического) отношения к действительности явлений реальности. В противоположность вероятностной математической идее психология восприятия говорит о том, что психологическое отношение к действительности не имеет абсолютного нуля отсчета и не предполагает того, что информация соотносится с ее отсутствием, а знание является нам на фоне незнания. Если в физике мы можем постулировать наличие света и яркости некоторого объекта по отношению к его полному отсутствию, то яркость в зрении соотносится скорее с некоторым средним ее значением, т.е. темнота в известной мере рядоположна свету. Свойства объектов и их предметные значения оказываются со- представленными в восприятии [15], а знания являются таковыми только в контексте других знаний.

При бросании кости вероятности событий (выпадения того или иного количества очков) вполне соотносятся с представленной выше стандартной моделью подсчета шансов. Однако шансы что-то узнать о кости как объекте совершенно другие, и они соотносятся с представлениями других наблюдений и экспериментов, в которых на практике одновременно увидеть можно не только две, но и три, а в целом и большее количество граней одной кости. Также можно представить себе игральную кость как общую объемную фигуру с соответствующим числом, расположением ее граней и изображениями на этих гранях. И это знание, как правило, предшествует модельным событиям.

Таким образом, можно утверждать, что в отличие от абстрактно-научной модели объективации действительности, фоном для которой является отсутствие знания, психологическая модель предполагает как раз наличие предварительного знания о предмете как в виде общей идеи наличия того или иного сопредставленного комплекса его свойств, так и непосредственно-чувственного способа осуществления действительности восприятия. Будучи со- представленными эти свойства представляет собой изначальный объектный контекст, включающий для двух событий, как их совместность, так и отдельность (т.е. конъюнкцию и дизъюнкцию их истинности) и их отношения с другими возможными объектами и событиями. События и объективируемые ими свойства по сути принципа их сопредставленности становятся связанными между собой.

Простым примером связанных между собой возможностей является падание сдвоенной монеты, которая может вдруг разделиться на две части наподобие раскрытия медальона, в котором снаружи есть, а внутри нет изображений «орла» и «решки» (рисунок 4.1) [19]. При падении такой монеты-медальона возможны (и можно для простоты считать что равновероятны) все четыре варианта событий: два варианта, когда монета-медальон падает как обычная монета, не раскрываясь, и два других варианта, когда монета-медальон падает, раскрываясь как медальон. При этом в одном случае «орел» и «решка» выпадают одновременно, а в другом - нет ни «орла» ни «решки».

Рис. 4.1. Пример монеты-медальона

Объединение событий здесь входит в общее число несовместных событий и подсчет вероятности событий в этом случае становится неоднозначным и в целом в ближайшем рассмотрении приводит к результатам отличным от случая событий для стандартной монеты (таблица 4.1).

Табл. 4.1. Таблица для подсчета шансов событий А и А&В

 

Вероятности событий A и A&B здесь оказываются одинаковыми и равными ¼. Таким образом, ясно, что подсчет вероятностей в целом сильно зависит от выбранного пространства элементарных событий и логических и других операций, которые часто негласно предполагаются осуществимыми на нем.

Например, допустим, что теперь нас интересует вероятность двух событий A и B. Тогда это совсем не обязательно именно логическая конъюнкция событий. В принципе все три варианта 1,1 1,0 и 0,1 тоже отвечают модели реальности в том смысле, что если оба свойства присущи предмету, то ему присущи и каждое из них в отдельности. Более того, если бы это было не так, то существование события A было бы невозможно. Это соответствует операции дизъюнкции и тогда вероятность A и B равна ¾, т.е. существенно больше, чем вероятность только одного события, равная ¼. (см. таблицу 4.2).

Табл. 4.2. Таблица для подсчета шансов конъюнкции и дизъюнкции

 

Таким образом, в психологической вероятностной модели, отвечающей идее со- представленности свойств, на вопрос: «Что более вероятно A или A и B?», вполне может следовать ответ: A и B - более вероятны. В стандартной модели случайные события соответствуют собственно отдельным операционным событиям, а в психологической модели требуется учет свойств, которые являются основой для возможности этих операционных событий - обеспечивают их общее происхождение и общий способ их представления.

Если стандартная модель идет от незнания (объективации) ситуации, то частная психологическая модель наоборот предполагает знание того, что, например, при детекции сторон монеты будет только два ответа («орел», «решка»), но никогда они вместе или их совместное отсутствие. Сравнивать вероятности событий A и/или A&B в этом случае на самом деле некорректно. Они не существуют в реальности как одновременные возможности. Первый случай предполагает только одну реализацию (эксперимент), а второй случай на самом деле возможен только, если произошли последовательно две реализации событий. Но в этом случае получить А&В в одной реализации невозможно.

Если же A и A&B события все же сравниваются в по-иному определенной (часто только умозрительной абстрактной) ситуации, то A по наличию этих свойств соответствует выделению чего-то одного из многого, т.е. отсутствию всего остального, что предполагает всего одно или малое количество благоприятных событий (т.е. является редким), а A и B (при том, что A полагается возможным быть без B) соотносится как раз с дизъюнкцией событий и тем самым предполагает большее количество благоприятных событий. Как показано ранее на примере монеты-медальона из этого вполне разумно следует, что вероятность события A и B должна быть больше или равна вероятности события A.

Интересно также, что, если при конъюнкции множество истинных событий является однозначным, то при дизъюнкции это множество многозначно. Это, в частности, приводит к сложностям в операциях измерения для квантовых явлений. Здесь надо принимать во внимание то, что физическая операционная ситуация двух измерений есть ситуация, в которой они не могут быть произведены одновременно (или вместе), что в квантовом выражении означает, что они несовместны (т.е. сами измерения настолько сильно влияют на измеряемый объект, что провести два эксперимента одновременно становится невозможно). В этом случае конъюнкция этих свойств, из которых одно измеряется в одном измерении, а другое в другом измерении, существует как операционное свойство, но дизъюнкция не обязательно существует как эксплуатационная характеристика [20].

Еще более показательным является рассмотрение вероятности событий в другой более многообразной модели вычисления вероятности выпадения численных значений, соответствующих граням в полуправильном многограннике - ромбокубооктаэдре (см. рисунок 4.2), если учитывать значения тех граней, чьи проекции на плоскость падения имеют не нулевую площадь. Это соответствует такой модели репрезентативности, доступности и достоверности, которая имеет место при восприятии данного объекта со стороны наблюдателя событий. Указанные выше грани могут быть визуализированы при одном броске данной фигуры, а находящиеся на этих гранях значения (или изображения) может считать человек, смотрящий перпендикулярно плоскости выпавшей грани [19].

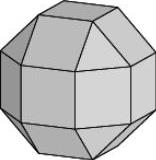
Рис. 4.2. Вид ромбокубооктаэдра

 

Для простоты положим, что вероятности выпадения каждой из 26 граней фигуры равны между собой. Тогда вероятность выпадения одной грани (событие А) равна 1/26. Вероятность получить А и В, соответствующие граням куба, из которого образован ромбокубооктаэдр, и не принадлежащие противоположным его граням, в одном событии, здесь (в отличие от обычного куба) уже не нулевая и равна 3/26, т.е. в целом в 3 раза выше, чем вероятность отдельного события.

Более точный расчет требует учета того, что в ромбокубооктаэдре 8 треугольников и 18 квадратов (6 в кубическом положении). В общем случае в силу не полной симметричности фигуры вероятности выпадения треугольника P3 и выпадения квадрата P4 не равны. Для общей вероятности появления любой из граней можно записать формулу: 8*P3+18*P4 = 1. Допустим, что вероятность P3 меньше P4: P3= 3*P4/4, тогда P4 = 1/24, P3 = 1/32.

Если событие A это выпадение грани квадрата, соответствующий граням куба, из которого образован ромбокубооктаэдр, а P(A&B) соответствует ситуации, когда две кубические грани окажутся рядом, то P(A) = P(B) = 1/24, а P(A&B) = 2/24, т.е. в два раза больше, чем P(A).

Будучи математической, рассмотренная сопредставленная вероятностная модель, на наш взгляд, более четко соответствует психологии восприятия человека и вместе с тем ее результаты согласуются с поведением людей при так называемой «ошибочной» оценке вероятности объединения событий [19].

5.       ЗАКЛЮЧЕНИЕ

Ставшие привычными научные представления часто используются в качестве норм и критериев истинности при оценке психологии человека. Это не всегда является адекватным реальной действительности и может приводить к своеобразным научным ошибкам и иллюзиям, имеющим стойкий характер в связи с общепризнанной важностью и значимостью научных и технологических знаний.

Принятие людьми решений в условиях неопределенности часто опосредуется простыми интуитивными эвристиками, которые не ограничены специальными научными закономерностями и с их точки зрения приводят к неверным результатам. В частности, в процессе оценки людьми вероятности будущих событий была выявлена проблема «ошибки объединения», связанная с нарушением людьми правила объединения вероятности случайных событий [1, 3-5].

В данной работе на основе представлений трансцендентальной психологии [12-16] предложен другой взгляд на эту проблему и показано, что «ошибку объединения» следует считать не столько ошибкой испытуемых, сколько стереотипной ошибкой исследователей, принимающих красивую теорию в качестве нормы там, где это применение не является вполне правомерным. При этом поведение людей при принятии эвристических решений можно считать вполне логичным и последовательным в представлении о том, что вероятность объединения событий часто вполне естественно является большей вероятности отдельных событий как таковых.

Свойства процесса восприятия как основа формирования, в том числе, эвристических представлений (о репрезентативности, доступности, достоверности и др.) в значительной мере обусловливаются качествами сопредставлености свойств объектов в процессе восприятия. Это соответствует иной математической модели, теоретические следствия которой согласуются с эвристическими экспериментальными результатами.

Представленная в работе модель сопредставленных событий наглядно демонстрирует, что вероятность объединения событий вполне может и даже должна превышать вероятность отдельных событий. Тогда вопрос верификации эвристических решений с помощью нормативного научного суждения получает иное решение, при котором проблема «Ошибки объединения» во многом снимается на основе признания ошибочности использования классической вероятностной модели для оценки правильности психологии поведения людей.

С качественной точки зрения можно констатировать, что поведение людей при оценке вероятностей не является реально соотносимым с правилом объединения вероятностей и факт следования правилу или нарушения его, скорее всего, не является в данном случае следствием учета или не учета этого правила (осознанно или неосознанно). Можно утверждать, что оценка вероятностей явным образом осуществляется на семантическом уровне с использованием общих моделей ситуаций и следующих из них событий и подчиняется логике причинных связей с учетом достоверности, сопредставленности и степени реальной встречаемости (правдоподобности) соответствующих событий [11, 19].

Это означает, что применение критериев классической теории вероятностей в качестве норм для оценки поведения людей в условиях неопределенности является неправильным, поскольку на практике речь идет о другой модели действительности, основанной на перцептивных, аффективных и семантических тенденциях, выраженных в многообразии причинно-связанных понятий и интенций. Эти понятия относятся как к репрезентативности и доступности, так и к достоверности, исключительности, сопредставленности, важности, применимости, правдоподобности, соответственности, доверительности, надежности и др. [10, 11].

В целом можно заключить, что принятие человеком решения в условиях неопределенности является полифункциональным процессом, который характеризуется сосуществованием различных (сознательных и бессознательных) тенденций, вносящих свой вклад в перцептивные и когнитивные способности чувствовать, понимать и распознавать явление предметов и ситуаций, раскрывать и конструировать содержания окружающего мира. Индивидуальная игра и взаимовлияние этих тенденций в случае слабо определенных ситуаций проявляется в наличие большого разнообразия многозначных вариаций ответов, существенно зависимых от контекстных влияний.

При этом среди указанных выше тенденций, несомненно, может присутствовать и та, в которой рассуждения согласуются со стандартной моделью теории вероятностей. Вместе с тем такое мышление не является приоритетным еще и потому, что оно относится к специфической группе явлений действительности и вряд ли является эволюционно и социально значимым.

В этой связи принятие правил специальной и явно упрощенной модели объединения вероятностей случайных событий в качестве нормы для оценки психологических процессов не кажется естественным. Использование этого нормативного поведения вне реальных границ его применимости и принятие его в качестве универсального мерила, применимого к реальности любых случайных событий, фактически приводит к возникновению научной иллюзии. Научно определенное нормативное рациональное поведение проецируется на психологию принятия человеком решений в условиях неопределенности, т.е. в область, которая далека от непосредственной применимости этого поведения, и рассматривается как некое собственно правильное поведение, универсально применимое в любых специфических обстоятельствах.

 

1. Канеман Д., Словик П., Тверски А. Принятие решений в неопределенности: Правила и предубеждения. — Харьков: Гуманитарный центр, 2005. — 632 с.
2. Хухлаева О.В., Чибисова М.Ю. Работа психолога в многонациональной школе. М.: Фо­рум, 2011. – 176 с.
3. Tversky A., Kahneman D. Judgment under uncertainty: Heuristics and biases. Science, 1974, 185, pp. 1124-1131.
4. Tversky A., Kahneman D. Extensional vs. intuitive reasoning: The conjunction fallacy in prob­ability judgment. Psychological Review, 1983, 90, pp. 293-3l5.
5. Heuristics & Biases: the psychology of intuitive judgement / edited by T.Gilovich, D.Griffin, D.Kahneman. Cambridge University Press. 2002. – 857 p.
6. Bonini N., Tentori K., & Osherson D. A Different Conjunction Fallacy. Mind and Language, 2004, 19 (5), pp. 574-575.
7. Sides A., et al. On the reality of the conjunction fallacy. Memory & Cognition. 2002,  30 (2), pp. 191-198.
8. Brachinger H. W., Monney P. A. The conjunction fallacy: explanations of the linda problem by the theory of hints. International Journal of Intelligent Systems, 2003, 18 (1), pp. 75 – 91.
9. Chase V. M., Hertwig R., Gigerenzer G. Visions of rationality. Trends in Cognitive Sciences, 1998, 2, (6), pp. 206-214.
10. Hertwig R., Gigerenzer G. The ‘conjunction fallacy' revisited: how intelligent inferences look like reasoning errors. Journal of Behavioral Decision Making, 1999, 12, pp. 275-305.
11. Artemenkov S.L. Kansei Versus Extensional Reasoning: The Scientific Illusion of The Con­junction Fallacy in Probability Judgment/ Proceedings of the First International Workshop on Kansei, 2006, pp. 8-11.
12. Миракян А.И. Контуры трансцендентальной психологии (книга 2), М.: Изд-во Институт психологии РАН, 2004. – 384 с.
13. Артеменков С.Л. Методология трансцендентальной психологии и проблемы моделиро­вания и экспериментального исследования порождающих процессов. Труды ФИТ (2). М.: РУСАВИА, 2005. с. 37-57.
14. Миракян А.И. Константность и полифункциональность восприятия — М., 1992. -216 с.
15. Кочурова Э.И. Принцип сопредставленности и полифункциональность восприятия. // Принципы порождающего процесса восприятия. / Под ред. А.И. Миракяна. -М., 1992. ­С. 159-170.
16. Миракян А.И. Афизикальные принципы психического отражения и их моделирование. // Принципы порождающего процесса восприятия. /Под ред. А.И.Миракяна. -М., 1992. -С. 9-46.
17. Хайдеггер М. Европейский нигилизм // Время и бытие: Статьи и выступления. – М.: Рес­публика, 1993. С. 63-177.
18. Григорян А.А. Закономерности и парадоксы развития теории вероятностей. Изд-во УРСС Москва, 2004. -120 с.
19. Artemenkov S. Scientific conceptions and heuristics in cross-cultural communication and edu­cation in terms of a joint probability decision making: The 11th international conference infor­mation technologies and management 2013. ISMA University of Applied Sciences, Riga, Lat­via, pp. 221-222.
20. Aerts, D., Aerts, S. Towards a general operational and realistic framework for quantum me­chanics and relativity theory. In A. C. Elitzur, S. Dolev and N. Kolenda (Eds.), Quo Vadis Quantum Mechanics? Possible Developments in Quantum Theory in the 21st Century. Berlin: Springer, 2004.