Алгоритм расчёта влияния эксперта на потребителя информации в социальных сетях и образовательных сайтах

Демонстрируется алгоритм оценки влияния, которое оказывает отправитель серии сообщений на по-лучателей этих сообщений в некоторой локальной социальной общности. Алгоритм строится на ос¬нове простой модели коллективного поведения индивидуумов при обмене информацией, когда в результате такого обмена получатель сообщения может изменить своё априорное мнение по поводу данного сообщения под действием аргументов отправителя. Суть оценки состоит в статистическом анализе согласованности мнений авторов сообщений и мнений получателей. На основе опроса сту¬дентов – гуманитариев по проблеме, для которой не может быть найдено обще-приемлемое решение, проведена оценка применимости этого алгоритма для количественного анализа степени воздействия отправителей сообщений на аудиторию. Воздействие определяется на основе факта изменения апри¬орного мнения индивидуума после получения сообщения (мнения отправителя) по тому же вопросу. Такой алгоритм может быть полезен для оценки эффективности воздействия на аудиторию сайтов с обучающим материалом со стороны носителей концепций, содержащихся в этом материале и для последующей коррекции или адаптации информационного материала, служащего для обучения и воспитания.

 

1.       ВВЕДЕНИЕ

Среди факторов, которые определяют эффективность обучения человека новым навыкам в рамках рабочей группы с общими интересами, или эффективность убеждения индивидуума в некотором местном сообществе о ценности системы взглядов, предложенных для обсуждения и принятия , являются: степень подверженности индивидуума влиянию других членов группы или других групп и собственные мотивации индивидуума. Собственные мотивации здесь не рассматриваются. Социум может повлиять на них через передачу знаний, умений, навыков. Но даже при наличии этих стимулирующих мотивацию качеств, индивидуум может не иметь общих с сообществом интересов в их использовании. В этой статье мы рассмотрим первый из этих двух факторов. Возможность измерения влияния отправителя сообщения на получателя полезна для определения эффективности убеждения, обучения, психологического или морального воздействия в условиях, когда за участниками дискуссии или диалога не закреплены формальным образом роли и позиции обучающего и обучаемого. На форумах и интернете, например, участники могут иметь различный статус, в зависимости от степени успешности их активности на форуме, но это не дает им полномочий командования, а дисциплинарное соподчинение между участниками форума не признается (не допускается).

Фактической оценке подвергается две характеристики членов некоего локального сообщества, а через них и характеристики всего выбранного локального сообщества. Это:

-        Степень воздействия той или иной информационной акции на локальное сообщество (можно говорить и о степени обучаемости сообщества и о возможности манипулирования групповым сознанием, то есть о позитивном и негативном воздействии на локальное сообщество близкими по характеру методами) ;

-        Степень сопротивляемости индивидуумов локального сообщества (по выборочной совокупности респондентов из этого сообщества) данному информационному материалу.

Первая характеристика показывает эффективность воздействия конкретных материалов или экспертов, вторая степень индивидуализма или конформизма членов данного локального сообщества.

Подобного рода задача ставилась П.С.Краснощековым, который предложил модель коллективного поведения людей (см., например гл 11.3. в [Васин, 2008], или начальную версию [Краснощеков, 1998]). (Недавно он вернулся к теме и сделал ряд уточнений и дополнений [Makagonov, 2014]). Им описана модель принятия решения индивидуумом, который руководствуется как своим личным отношением к обсуждаемому вопросу, так и отношением к этому вопросу окружающих его субъектов. Индивидуум должен сделать выбор между двумя вариантами - принять одно из двух альтернативных решений, занять одну из двух альтернативных позиций.

По условию, влияние каждого j -го члена сообщества на i - го индивидуума не зависит от влияния других членов и определяется числом λij - вероятностью того, что i - ый индивидуум примет (будет разделять) позицию (состояние) j -го с той же вероятностью Pj, с которой это состояние испытывает воздействующий на него j -й. Для индивидуума, не имеющего своего устойчивого мнения, вероятность нового состояния, после воздействия остальных членов сообщества выражается формулой

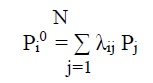                                   (1)

где λii =0 (то-есть, самоубеждение в этой формуле не рассматривается, так как по условию индивидуум не имеет своего устойчивого мнения), все λij неотрицательны, а их сумма равна единице:

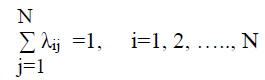                       (2)

N - число членов сообщества, могущих оказывать влияние на других.

                 (3)

Или, подробнее:

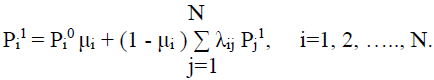                     (4)

При заданных параметрах  можно посчитать значения . Однако, общего метода расчета этих параметров П.С. Краснощеков не приводит, а использует гипотетические модели, для которых параметры определяет на основе здравого смысла.

Ранее в [Расторгуев] был предложен алгоритм вычисления коэффициентов  для этой модели применительно к оценке меры взаимовлияния членов форума в локальной социальной сети.

Для измерения влияния, которое отдельные члены группы оказывают на других, и степени конформизма личности, мы используем семантико-логический анализ (с количественными выводами) сообщений на форуме, который содержит обсуждение проблем и инноваций.

Мы используем метод кластерного анализа, чтобы найти сходства и расхождения между членами форума и классифицировать их, выявляя, таким образом, какие из них являются активными лидерами и оказывают влияние на других.

Рассмотрим далее алгоритм и процедуру оценки влияния экспертов на респондентов из некоторой локальной социальной общности, объединённой по каким-либо признакам (территориально-средовым, образовательно-деятельностным, и т. п.), связанным с групповым сознанием (поведением).

Для оценки выбрана форма опроса-диалога, в котором респонденту предлагается высказать свое мнение по вопросу, по которому у глобального сообщества нет единого мнения. Вопросы закрытые, с заданным набором возможных ответов, или полузакрытые, с заданным диапазоном количественных оценок. Перед ответом на закрытый вопрос - «оценить мнение эксперта» - респонденту сообщается аргументация эксперта, обосновывающая это мнение. Таким образом, оценке подвергается не просто выбор эксперта, но и его обоснованность с точки зрения респондента. Значит, по оценке респондента можно оценить влияние аргументов эксперта на позицию респондента, на его собственную позицию по обсуждаемому вопросу.

2.       ПОСТАНОВКА ЗАДАЧИ

Поменяем условия, примем гипотезу о том, что индивидуум с номером j должен сделать выбор не в пользу или против одного варианта (состояния А), а между тремя различными (не- пересекающимися) вариантами. Предположим теперь, что всего возможно в данном случае несколько состояний: А1, А2, ..., Ак и требуется указать вероятности P(A1,j), P(A2,j) или P(Ak,j) своих предпочтений в отношении вариантов состояния А(1, j), А (2,j) ...А(к,]).

Будем здесь рассматривать не больше трех вариантов (к=3) по двум причинам:

- Обобщение на произвольное конечное число альтернатив не представляет трудностей;

- Сведения, основанные на контент-анализе сообщений, трудно разделить на очень большое количество статистически значимых альтернатив.

В соответствии с вышеприведенными формулами в отношении этих предпочтений индивидуум имеет своё мнение с одной и той же степенью уверенности. Это соответствует оценке его характера с помощью коэффициента μ_i, который должен иметь одно и тоже значения μ_i (А1) = μ_i (А2) = μ_i (А3) для каждого варианта.

Выражение  под знаком суммы в формуле (4) для каждого варианта: А1, А2, А3 имеет множителем вероятность . Однако, эта вероятность имеет также одно и то же значение для всех вариантов, так как зависит не от рассматриваемого варианта состояния А, а от степени влияния j -го члена сообщества на i - го индивидуума: . Индивидуум с номером «i» находится под влиянием аргументов индивидуума «j» вне зависимости от того, являются ли высказывания последнего за А1, А2 или А3. Учёт долей высказываний за каждый из вариантов обеспечивается вторым множителем в этом выражении: Pj(A 1), Pj(A2), или Pj(A3).

В случае L высказываний против одного из вариантов А1, А2 или А3, например, против А1, его учитывают как высказывание за А2 и А3, в пропорции L*Pj(A2) b L* Pj(A3).

Пусть на индивидуума воздействуют эксперты с разными мнениями по каждому из альтернативных вариантов, с различной аргументацией в пользу и против каждого варианта. Тогда эти эксперты по существу выступают конкурентами в борьбе за выбор, который предстоит сделать членам сообщества. Сами эксперты в соответствии с инструкцией или по убеждению не меняют своего мнения (р эксперта равно единице). Поэтому относящаяся к ним система уравнений, аналогичная системе (1) должна распасться на независимые между собой тройки уравнений для каждого индивидуума, при этом каждая тройка относится к одному индивидууму или к тем, которые имеют одинаковое поведение в течение всего периода наблюдений.

3.          ВЫБОР ВОПРОСНИКА ДЛЯ ИССЛЕДОВАНИЯ

В качестве материала для вычислительного эксперимента был сформирован вопросник следующей структуры:

Сведения о респонденте: Пол (Х0). Возраст (Х1). Факультет (Х2). Курс (Х3). Семейное положение (Х4).

Собственно опрос по теме исследования влияния высказываний на респондента.

3.1.     Выбор темы и структуры опроса

Для чистоты эксперимента вопросы не должны иметь очевидных ответов. Лучше, чтобы вопросы вообще не имели «правильных» ответов. Выбор пал на гипотетическую ситуацию, широко обсуждаемую в интернете, в том числе профессиональными психологами и ведущими тренингов (см., например [7-12]): Вы спаслись в катастрофе и у Вас есть возможность спасти только одного человека из трёх

- мать (вариант 1), супруг(а/у) (вариант 2) или - своего ребенка (вариант 3).

Первый вопрос: Кого бы спасали Вы? (указать номер варианта). Этот вопрос широко обсуждается в интернете. В действительности он интересен тем, что по ответам на него имеется некоторая статистика, различная для разных типов национальных культур, и имеется сравнительно большой набор аргументов в пользу того или иного выбора. Эти аргументы можно предъявлять респондентам, чтобы они оценивали выбор внешних экспертов с учетом мотивировки последних.

Далее респонденту последовательно сообщается статистика выбора с господствующей мотивировкой:

-          в одной западной стране (Индекс обобщённого эксперта W),

-          в одной восточной стране (Индекс E),

-          в Российском портале ОТВЕТЫ.ру (Индекс N), и

-          среди жителей юга Мексики(Индекс S).

После оглашения данных по каждой выборке в отдельности респонденту предлагается оценить по трёхбалльной шкале своё отношение (-1; 0; +1) к выбору вариантов внешними экспертами. Эти варианты представлены в таблице 1.

Таблица 1.

 

Респондентам также были заданы вопросы: какой выбор предпочитают они: V1, V2 или V3 и какой выбор, по их мнению, сделал бы средний россиянин B1,B2,B3.

Результаты обсуждаются в следующих разделах, а суммарные результаты опроса даны в двух последних строках таблицы №1.

4.      ФОРМИРОВАНИЕ ВЫБОРКИ И ПЕРВИЧНЫЕ РЕЗУЛЬТАТЫ ОПРОСА

В качестве генеральной совокупности было выбрано множество студентов РАНХиГС, обучающихся на гуманитарных специальностях.

Удалось получить анкеты опроса 32 респондентов

Характеристика опрошенных: из тридцати двух опрошенных 9 человек мужского пола 23 - женского.

Для оценки представительности выборки по этому показателю требуется знать соотношение полов по всей генеральной совокупности опрошенных категорий.

Х1: Средний возраст 19,6 весь диапазон = 18-22

Таблица 2. Распределение респондентов по возрасту.

 

Х4: сем положение: 5 из 32 - женихи или невесты 1 замужем.

Для оценки представительности выборки по показателям Х0, Х1 и Х4 требуется знать соотношение полов по всей генеральной совокупности опрошенных категорий.

Показатели Х2, Х3 - принадлежность факультету и курсу сведены в таблицу 3:

Таблица 3.

 

Х2: 20 человек из 32 - студенты ФГУ

Х3: Половина опрошенных - студенты 3-го курса.

С точки зрения распределения характеристик Х2 Х3 выборка нерепрезентативна.

Однако степень влияния этих характеристик может быть несущественной, что можно проверить методом кластеризации. А именно: если эти характеристики не влияют на выбор варианта ответа у респондента, то эти характеристики должны быть представлены равномерно в каждом кластере.

По условиям опроса каждый респондент оценивает только одно суждение каждого внешнего эксперта, поэтому для одного опрашиваемого подсчёт коэффициентов влияния Ху и pi даёт грубые простые результаты. Описанная в [Makagonov, 2014] , ранее разработанная нами методика не работает, так как там у каждого опрашиваемого фиксировалась статистика его выбора в нескольких опытах (сеансах дискуссий с тем же внешним экспертом). Статистика оценок его отношения к выбору альтернатив внешними экспертами позволяла там посчитать отношение согласий к сумме согласий и несогласий.

В нашем варианте опроса вместо одного опрашиваемого в нескольких опытах приходится взять несколько опрашиваемых в одном опыте. Эти опрашиваемые по поводу мнения одного внешнего эксперта должны быть подобны, например, принадлежать одному кластеру с общими значениями показателей. Поэтому перед статистической обработкой и подсчётом коэффициентов влияния приходится разбивать всех респондентов на кластеры. Естественным в данном случае является объединение в один кластер респондентов с одинаковым ответом на вопрос, кого бы спасали они (варианты V1, V2 , V3). (По условиям опроса они не могут разбить свои предпочтения на части).

Совместный кластерный анализ характеристик Х0-Х4 и вариантов V1, V2, V3 для 32-х респондентов показал, что главными характеристиками, влияющими на образование кластеров респондентов (без учёта оценок ими выбора внешних экспертов) явились три показателя: семейное положение, варианты выбора V3 и E3. При этом максимальное значение характеристики V3 оказалось у всех респондентов первого и второго кластеров: R1, R3, R6, R7, R9, R10, R11, R12, R13, R14, R15, R16, R17, R18, R19, R20, R23, R25, R26, R28, R29, R30 всего у 22 респондентов из 32.

5.      ПОДСЧЁТ КОЭФФИЦИЕНТОВ ВЛИЯНИЯ λij И μi И ВЕРОЯТНОСТЕЙ Pi1 И Pi .

С учётом алгоритма, изложенного в [Makagonov, 2014], и в связи с переходом от одновариантного выбора (A или не А (А)) к многовариантному (в эксперименте - трёхвариантному), вычисление априорных вероятностей и коэффициентов сводится к следующим процедурам:

Вероятности состояний А1, А2 и А3 у отправителей сообщений определены заранее.

Оценки вероятности среднего априорного выбора респондентов определяются по формуле

P (Ai) = количество случаев выбора Ai / (сумма всех случаев выбора)

Оценки вероятности среднего мнения респондентов о выборе среднего россиянина подсчитываются аналогично.

Значения процентных долей, соответствующих этим оценкам вероятностей, приведены в таблице 1 в последних двух строках.

5.1.         Вычисление μ

Мы выполняем эту операцию для каждого из сообщений и для всех пассивных экспертов. Затем для каждого пассивного j-ого эксперта мы получаем меру независимости мнения μ, которые мы используем в формуле (4).

Это можно сделать, только если пассивные эксперты искренни и ответственно относятся к производимому ими анализу, а не расставляют оценки случайным образом. Люди не меняют своё мнение слишком часто, поэтому μ отражает свойство характера индивидуума и эту характеристику можно использовать при измерениях в других обсуждениях с их участием.

Поэтому для расчёта μ в Excel мы используем следующий алгоритм:

-         Находим во всех высказываниях их направленность «за Ai» или «против Ai».

-         В строке L под строкой высказываний мы помещаем логическую характеристику в форме 1 для состояния A и -1 для состояния А.

-         Мы просим участников оценки выразить своё мнение в форме «1» в случае согласия, «0» - если их мнение не сложилось, и -1 если они не согласны с идеей состояния А. Эти значения помещены в строках i=L+1,L+2,L+3,L+4);

-         Если оценщик полностью поддерживает все высказывания активных экспертов (оценки совпадают) тогда оценщик является полным конформистом и его коэффициент μ следует приравнять нулю.

-         Если оценщик не согласен со всеми высказываниями, тогда он имеет коэффициент р равный единице.

-         Если мы сравниваем K пар оценок в строке L и в каждой из строк от L+1 до L+4 и среди них имеются расхождения, то р равно сумме всех расхождений, делённой на K (количество пар).

Расчёты, проведённые по этому алгоритму дали значения μ для трёх обобщённых оценщиков, осреднённых представителей кластеров выбравших для спасения мать (M), супруга (S ) и своего ребёнка (CH), дали следующие результаты:

В случае, если индивидуум не может участвовать в оценке, но он высказал сам свое мнение по каждому вопросу, который еще не обсуждался им с экспертами, то в этом случае можно с какой-то степенью уверенности предсказывать поведение оценщика по каждому высказыванию эксперта. Тогда можно фиксировать только отклонения от этих предсказаний, и они определят влияние активных экспертов на мнение оценщика.

5.2.          Вычисление λ

Как было сказано выше, для получения статистики оценок вместо одного опрашиваемого в нескольких опытах приходится взять несколько опрашиваемых, принадлежащих одному кластеру с близкими значениями показателей.

Когда одно высказывание оценивают несколько членов одного кластера, то суммирование совпадений и несовпадений производим по всем оценкам представителей одного кластера оценщиков всех (трёх) высказываний одного активного эксперта. Итак, имеется три кластера оценщиков, в каждом из кластеров собраны оценщики, голосовавшие за одно из состояний A1, A2, или A3. Из статистики этих оценок находим λ по следующему алгоритму:

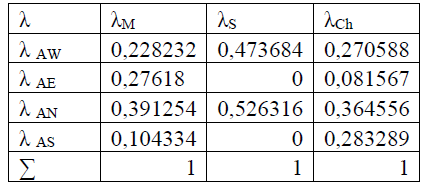
Например, для 22-х оценщиков, выбравших априорно состояние A3=Ch, выбор эксперта W (WM,WS; WCh) и результаты вычисления значений R и C приведены в таблице 4.

Таблица 4.

 

Отсюда L(Ch,W)=C/(C+R)= 0,701754. Вычислив каждое и после нормирования их, получаем

Аналогично для 22 оценщиков, выбравших априорно состояние A3=Ch, выбор эксперта E (EM,ES; ECh) и вычисление значений R и C приведены в таблице 5.

Таблица 5.

Таблица 6.

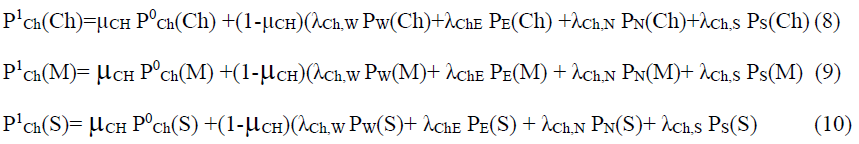
Особенностями этих трёх формул являются следующие:

-         Часть априорных вероятностей выбора этих 22 оценщиков равна нулю;

-         Все (k=1,2,3,4) одинаковы для каждого из значений k.

-         Эксперты по условиям проведения эксперимента не участвуют в явном виде и на них респонденты оценщики не могут оказать влияния, поэтому априорные и апостериорные вероятности выбора активных экспертов совпадают и поэтому верхний индекс опущен, а сами эти вероятности связаны соотношением

Поскольку равны нулю, а их апостериорные аналоги в большинстве своём отличны от нуля, то очевидно, что часть оценщиков в процессе ознакомления с мнениями активных экспертов переходях из своего кластера в другой. Это означает, что вероятность каждого апостериорного состояния должна быть собрана из вычислений по формулам типа (8-10) как взвешенная сумма апостериорных вероятностей для каждой группы. Например, итоговое значение апостериорной вероятности выбора состояния Ch должно быть посчитано по формуле:

Сумма этих финальных апостериорных вероятностей должна быть равна единице. Эти замечания отражены в нижеследующей таблице 7.

Таблица 7.

 

Взвешенные суммы апостериорных вероятностей для каждой группы представлены в строке Pacad(a posteriori) нижеследующей таблицы 8.

Таблица 8.

 

Рассмотренный эксперимент в пределах имеющейся выборки показывает, что информирование оценщиков о мнениях других экспертов сильно и не вполне предсказуемо влияет на мнение респондентов

6.      ЗАКЛЮЧЕНИЕ

Выбор вопросника проведён с целью предъявления респондентам вопросов, не имеющих однозначного предсказуемого ответа.

В рассмотренном эксперименте помимо вычисления изменения вероятностей исходного состояния каждого оценщика, требуется подсчитывать вероятности смены состояния и пересчитывать баланс апостериорных состояний.

При последующих опросах тех же респондентов по близкой тематике можно надеяться на сохранение характера респондентов, а значит и сохранения значения р, однако пока этот момент остаётся гипотезой, подлежащей проверке.

Рассмотренный случай трёх вариантов очевидным образом распространяется на произвольное число вариантов.

Формула (1) преобразуется к виду

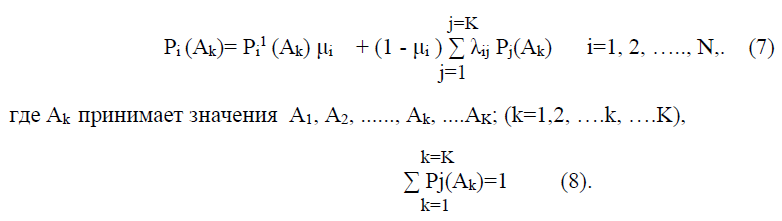
В рассмотренном эксперименте активные эксперты не обмениваются мнениями между собой, поэтому система сильно упростилась, фактически распавшись на отдельные группы уравнений (по три в каждой группе), но общий алгоритм остаётся невырожденным и все выводы справедливы и для общего случая.

Наиболее сложным шагом в описанной методике остаётся контент-анализ для оценки суждений экспертов, но эта операция не столь трудоёмка при ограниченном числе оцениваемых высказываний.

Разработанная методика может быть рекомендована как для анализа степени обучающего воздействия, или качества учебного материала, выставленного на сайте или на форуме.

Она же может применяться и для оценки раздаточного учебного материала при любых формах обучения.

 

1. Васин А.А., Краснощеков П.С., Морозов В.В. Исследование операций. − М. Издатель­ский центр «Академия». 2008. ISBN 978-5-7695-4190-2. -464 с.
2. Краснощеков П.С. Простейшая математическая модель поведения. Психология конфор­мизма. − Математическое моделирование, 1998, т.10, №7, с.76-92.
3. Makagonov P., Dorado R.M.V., Espinoza C.B.R. Measure of Mutual Influence among Mem­bers of a Social Network. – Моделирование и анализ данных, 2014, №1, с. 64-73.
4. Расторгуев C.П. Выборы во власть как форма информационной экспансии,1999.
5. Васин А.А. Эволюционная теория игр и экономика. Ч. 2. Устойчивость равновесий. Особенности эволюции социального поведения. – Журнал новой экономической ассоци­ации, 2010, №5, с.10-27.