В статье излагается методология разработки пакета расширения СКМ Mathcad MLSY_SM_UP+Mathcad, где в качестве базиса используется система сжатий и сдвигов атомарной функции UP(x). Показан метод разработки программного модуля, формирующего базис, и метод формирования ДНПФ дифференцирующего звена второго рода в СКМ Mathcad. Работа разработанного пакета расширения демонстрируется на примере анализа и параметрического синтеза системы управления самонаводящейся ракеты.
ВВЕДЕНИЕ
В наше время является актуальной задача проектирования современных систем автоматического управления, таких как система управления мягкой посадкой космических аппаратов на различные планеты солнечной системы, системы управления летательными аппаратами. Исследовать такие системы управления помогают разного рода пакеты расширения для СКМ. Эти программные комплексы не содержат пакеты программ, где в качестве базиса используется система сжатий и сдвигов атомарной функции up(x) [Рвачев, 1978]. Целью данной работы является разработка пакета расширения MLSY_SM_UP+Mathcad и элементарных алгоритмов спектрального метода по системе сжатий и сдвигов атомарной функции up(x). На первом этапе для пакета расширения MLSY_SM_UP+Mathcad были реализованы и добавлены программные модули, содержащие реализацию самой атомарной функции up(x) и систему сжатий и сдвигов атомарной функции up(x). На втором этапе был разработан пакет расширений MLSY_SM_UP+Mathcad, содержащий элементарные алгоритмы спектрального метода. На третьем этапе разработанный пакет расширения MLSY_SM_UP+Mathcad применен для решения различных примеров. В итоге разработана атомарная функция up(x). Сформирована система сжатий и сдвигов атомарной функции up(x). А результатом выполненной работы является вывод элементарных алгоритмов спектрального метода по системе сжатий и сдвигов атомарной функции up(x). Работа разработанного пакета программ демонстрируется на примере анализа и параметрического синтеза системы управления самонаводящейся ракеты.
1.ПОСТАНОВКА ЗАДАЧИ

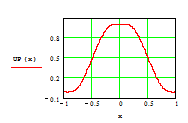
Рис. 1. График функции up(x)
2. ПАКЕТ РАСШИРЕНИЯ MLSY_SM_UP+MATHCAD


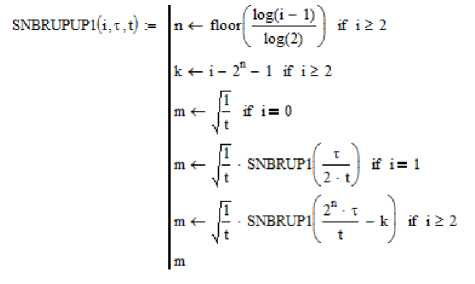
Рис. 2. Программный модуль, формирующий базис {rupi(t,r)}
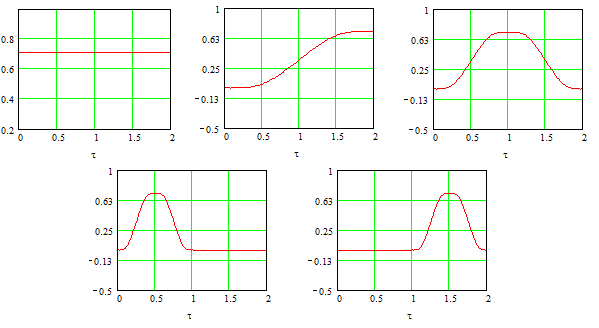
Рис. 3. Графики функций rupi (t,r), где i=1, 2, 3, 4


Рис. 4. Программный модуль вычисления НСХ
Далее опишем реализацию наиболее сложного звена - дифференцирующего звена второго рода. Для этого необходимо найти его ДНПФ. В первую очередь найдем производную от базисной функции.
В [Кравченко, 2003] приведен алгоритм, по которому меняется функция up(x) при дифференцировании. Реализуем этот алгоритм (рис. 5). В программу передается параметр n - порядок производной. На рис. 6 представлен результат работы данной программы.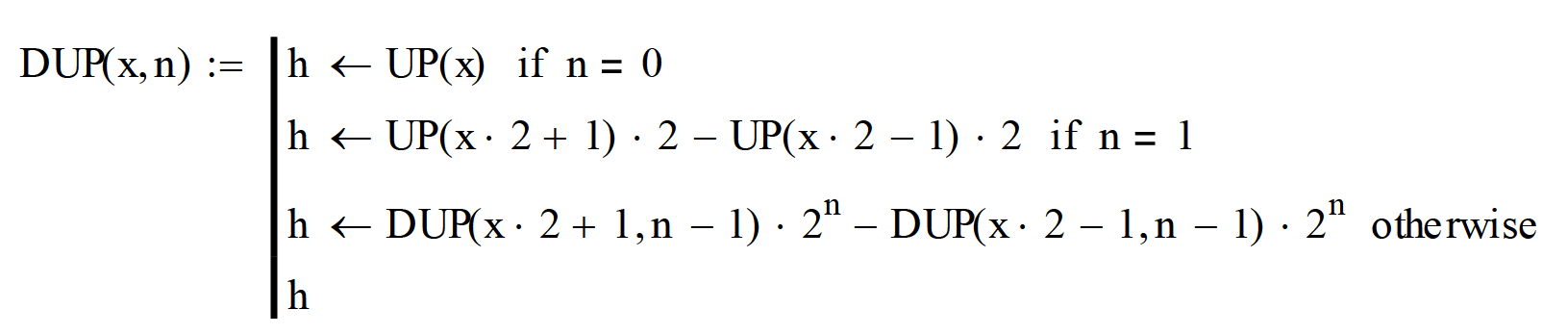
Рис. 5. Программный модуль вычисления производной от функции up(x)
Теперь построим производные от всех базисных функций. Их реализация почти полностью совпадает с реализацией построения базиса по системе сжатия и сдвига функции up(x) описанной выше, добавляются лишь коэффициенты, возникающие в результате дифференцирования. Программный модуль приведен на рис.7. Параметры, которые передаются в программный модуль, также описанный выше, лишь стоит отметить, что n - порядок дифференцирования. Пример работы данного модуля приведен на рис. 8 для производной первого и второго порядка соответственно.
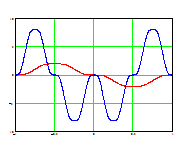
Рис. 6. График первый и второй производной от функции up(x)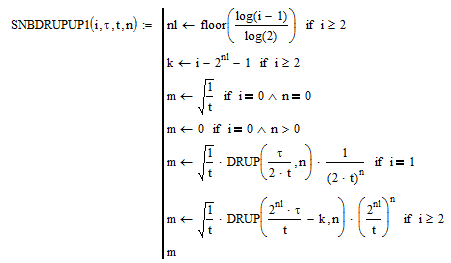
Рис. 7. Программный модуль вычисления производных от базисной функции восстановления rupi (t,r)
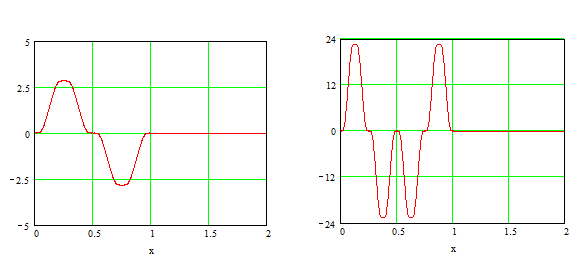
Рис. 8. График первой и второй производной от базисной функции rup3(t,r)


Рис. 9. Программный модуль вычисления ДНПФ дифференцирующего звена первого порядка первого рода
Примечание: алгоритмы вычисления ДНПФ остальных элементарных звеньев схожи по реализации.
3.ПРИМЕР АНАЛИЗА И ПАРАМЕТРИЧЕСКОГО СИНТЕЗА СИСТЕМЫ УПРАВЛЕНИЯ САМОНАВОДЯЩЕЙСЯ РАКЕТЫ


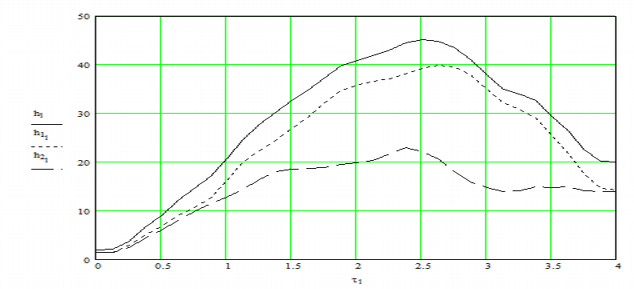
Рис. 10. Средние квадратичные значения переходных процессов

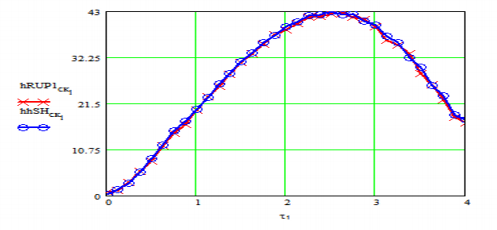
Рис. 11. График среднего квадратичного значения переходного процесса
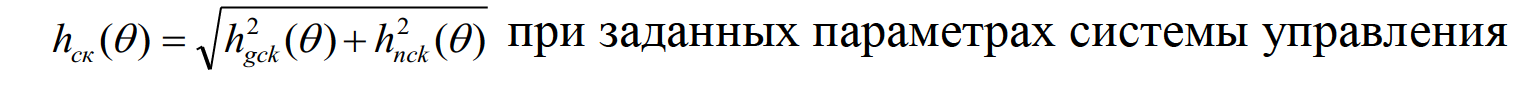
ВЫВОДЫ
