О субоптимальном решении задачи быстродействия для линейной дискретной системы в случае несимметричных ограничений на управления

В.М. Подгорная

doi:10.17759/mda.2024140304

Введение

Дискретный принцип максимума часто используется для решения задач оптимального управления дискретными системами в качестве необходимых, а иногда и достаточных условий оптимальности процесса. В частности, для линейных систем он является необходимым и достаточным условием [2, 11]. Принцип максимума испытывает сложности при рассмотрении вырожденных задач, то есть тех, для которых оптимальное значение достигается во внутренней точке множества достижимости [Пропой, 1973], это приводит к вырождению траектории сопряженной системы и, как следствие, к невозможности вычислить оптимальное управление из его соотношений. Одной из таких задач является задача быстродействия, которая характеризуется дискретным критерием качества, то есть числом шагов, необходимым для перевода системы в начало координат, которое не может быть вычислено из дискретного принципа максимума.

Среди актуальных исследований на тему решения задачи быстродействия для линейных дискретных систем можно выделить следующие работы.

В [Abdelhak, 2010] рассматривается смешанный функционал, включающий в том числе и время, но за счет второго слагаемого в функционале не происходит вырождения. В [Bako, 2011] предложен подход к решению задачи быстродействия, основанный на разреженной оптимизации множества состояний, то есть минимизации количества ненулевых элементов из множества состояний. В [Discrete-Time System Optimal, 2018] решается задача управления путем дискретизации по Годунову дифференциального уравнения в частных производных Лайтхилла–Уильямса–Ричардса. С использованием метода дискретных сопряжений результирующая нелинейная задача оптимального управления сводится к системе градиентных вычислений.

Если время вычислено и зафиксировано, то задача обладает вырожденностью с точки зрения построения сопряженной траектории. Поэтому оказывается актуальным исследование различных подходов к регуляризации принципа максимума. В частности, в работе [9, 6] одним из таких методов регуляризации является сужение множества допустимых значений управлений для того, чтобы терминальное состояние оптимальной траектории находилось в граничной точке множества достижимости. Это приводит к возможности составить конструктивные соотношения принципа максимума, из которых может быть построен процесс. Сложностью такого подхода является численное разрешение полученных условий.

В работах [7, 8] рассматривается задача сведения соотношений регуляризованного принципа максимума к системе алгебраических уравнений для суперэллипсоидальной структуры множества допустимых значений управлений при помощи аппроксимационных методов. Суперэллипсы в качестве аппроксимирующих множеств обладают большим числом степеней свободы, чем эллипсы. Хотя существует ряд приложений данного класса множеств в прикладных и теоретических задачах [13, 15, 17], их аппарат на данный момент является плохо исследованным. Данная работа продолжает результаты [7, 8], расширяя возможности суперэллипсоидальных аппроксимаций за счет выбора центра множества в приложении к решению задачи быстродействия.

Обозначения

Будем полагать, что фазовое пространство является евклидовым пространством

R^{n}

со скалярным произведением, определяемым соотношением

(x, y) = \sum_{i = 1}^{n} x_{i} y_{i} .

Для произвольного

r \in [1; + \infty)

введем на

R^{n}

норму

{‖ x ‖}_{r} = {(\sum_{i = 1}^{n} {| x_{i} |}^{r})}^{\frac{1}{r}} .

При

r = 2

норма

{‖ ∙ ‖}_{2}

оказывается согласованной со скалярным произведением. Значение

r = 1

с точки зрения теории является допустимым, но в рамках данной статьи рассматриваться не будет, что позволяет определить число

q > 1

как двойственное по Гельдеру числу

r

:

\frac{1}{r} + \frac{1}{q} = 1.

Для произвольных множеств

X, U \subset R^{n}

и матрицы

D \in R^{n \times n}

через

X + U

будем обозначать сумму по Минковскому [12, §3 гл. I]

X + U = {x + u : x \in X, u \in U},

а через

D U

– образ множества

U

при воздействии на него отображения

D

D U = {Du : u \in U} .

Через

\partial U

и

\int U

обозначим множества граничных и внутренних точек

U

соответственно. Под

cone {U}

будем понимать коническую оболочку множества

U

[12, §2 гл. I].

Если множество

U \subset R^{n}

является выпуклым компактом, то для произвольной точки

u \in U

через

N (u, U)

обозначим нормальный конус множества

U

в точке

u

[12, §2 гл. I]:

N (u, U) = {p \in R^{n} 0} : (p, u) = \max_{\tilde{u} \in U} (p, \tilde{u})} .

Элементы нормального конуса

N (u, U)

называются векторами, опорными к

U

в точке

u

. Заметим, что по построению

N (u, U) = \emptyset

тогда и только тогда, когда

u \in \int U

. Если также верно включение

0 \in \int U

, то

U

будем называть выпуклым телом [10, раздел 3 §1 гл IV] и для произвольного

x \in R^{n}

введем функционал Минковского [10, раздел 3 §2 гл. III] или калибровочную функцию [12, §4 гл. I]:

M (x, U) = \inf {t > 0 : x \in t U} = \inf {t > 0 : \frac{x}{t} \in U} .

Под строго выпуклым множеством

U \subset R^{n}

будем понимать такое множество, что для любых

u^{1}, u^{2} \in U, λ \in (0; 1)

верно включение

λ u^{1} + (1 - λ) u^{2} \in \int U

.

Будем называть суперэллипсом или суперэллипсоидальным множеством для некоторых

a_{1} > 0, \dots, a_{n} > 0, r > 1

множество вида

E_{r} (a_{1}, \dots, a_{n}) = {x \in R^{n} : \sum_{i = 1}^{n} {| \frac{x_{i}}{a_{i}} |}^{r} \leq 1} . (1)

Для краткости будем полагать

a = {(a_{1}, .., a_{n})}^{T}

и обозначать соответствующий суперэллипс через

E_{r} (a)

. Под

diag (a) \in R^{n \times n}

будем полагать диагональную матрицу, построенную из вектора

a \in R^{n}

:

diag (a) = (\begin{matrix} a_{1} & 0 & \dots & 0 \\ 0 & a_{2} & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & a_{n} \end{matrix}) .

Постановка задачи

Рассматривается линейная дискретная система с ограниченным управлением

(A, U)

:

\begin{matrix} x (k + 1) = Ax (k) + u (k), \\ x (0) = x_{0}, u (k) \in U, k \in N \cup {0}, \end{matrix} (2)

где

x (k) \in R^{n}

– вектор состояния системы,

u (k) \in R^{n}

– управляющее воздействие,

A \in R^{n \times n}

– матрица системы,

U \subset R^{n}

– множество допустимых значений управлений. Предполагается, что

\det A \neq 0

,

U

– выпуклый компакт,

0 \in \int U

.

Для системы (2) решается задача быстродействия, т.е. требуется перевести систему

(A, U)

из заданного начального состояния

x_{0} \in R^{n}

в начало координат за минимальное число шагов

N_{\min}

:

N_{\min} = \min {N \in N \cup {0} : \exists u (0), \dots, u (N - 1) \in U : x (N) = 0} .

Процесс управления

{x^{} (k), u^{} (k - 1), x_{0}}_{k = 1}^{N_{\min}}

, удовлетворяющий условию

x^{} (N_{\min}) = 0

, будем называть оптимальным. Предполагается, что задача быстродействия для системы

(A, U)

разрешима, т.е.

N_{\min} < \infty

. Подробно вопросы разрешимости задачи быстродействия для системы (2) рассмотрены в [Берендакова, 2023].

Построение оптимальных по быстродействию процессов сильно связано с аппаратом множеств 0-управляемости [5, 9].

Для произвольного

N \in N \cup {0}

обозначим через

X (N) \subset R^{n}

множество 0-управляемости системы (2) за

N

шагов, т.е. множество тех начальных состояний, из которых систему (2) возможно перевести в 0 за

N

шагов посредством выбора допустимых управляющих воздействий:

X (N) = {\begin{matrix} \begin{matrix} {x_{0} \in R^{n} : \exists u (0), \dots, u (N - 1) \in U : x (N) = 0}, & N \in N, \\ {0}, & N = 0. \end{matrix} \end{matrix} (3)

Тогда согласно определению

N_{\min}

также справедливо представление:

N_{\min} = \min {N \in N \cup {0} : x_{0} \in X (N)} . (4)

При этом управление, как продемонстрировано в [4, 6], оптимально тогда и только тогда, когда для всех

k = \bar{0, N_{\min} - 1}

верно включение

x^{} (k + 1) = A x^{} (k) + u^{} (k) \in X (N_{\min} - k - 1) .

В [Ибрагимов, 2017] получен ряд результатов для задачи быстродействия, которые можно представить в форме принципа максимума для строго выпуклого

U

.

Теорема 1 ([9, теоремы 1–2]). Пусть

U \subset R^{n}

– строго выпуклое и компактное множество,

0 \in \int U

,

\det A \neq 0

, класс множеств

{X (N)}_{N = 0}^{\infty}

определяется согласно (3), процесс управления

{x^{} (k), u^{} (k - 1), x_{0}}_{k = 1}^{N_{\min}}

и траектория сопряженной системы

{ψ (k)}_{k = 1}^{N_{\min} - 1}

удовлетворяют соотношениям

\begin{matrix} x^{} (k + 1) = A x^{} (k) + u^{} (k), \\ u^{} (k) = α \arg \max_{u \in U} ({(A^{- 1})}^{T} ψ (k), u), \\ ψ (k + 1) = {(A^{- 1})}^{T} ψ (k), \\ x^{} (0) = x_{0}, \\ - ψ (0) \in N (x_{0}, α X (N_{\min})), \\ α = M (x_{0}, X (N_{\min})) . \end{matrix}

Тогда

1. ${x^{} (k), u^{} (k - 1), x_{0}}_{k = 1}^{N_{\min}}$ – оптимальный по быстродействию процесс системы $(A, U)$ ;
2.если $α = 1$ , то оптимальный процесс единственный;
3. $- ψ (k) \in N (x^{} (k), α X (N_{\min} - k)), k = \bar{0, N_{\min} - 1}$ .

С вычислительной точки зрения вопрос применения теоремы 1 сводится к определению

α

и

ψ (0)

из условий

\begin{matrix} - ψ (0) \in N (x_{0}, α X (N_{\min})), \\ α = M (x_{0}, X (N_{\min})), \end{matrix} (5)

что в случае произвольного выпуклого тела

U

может быть нетривиальной задачей.

В [Ибрагимов, 2023а] представлен метод формирования субоптимального управления, основанный на использовании аппроксимации

U

множеством вида

\hat{U} = B E_{r} (a), B \in R^{n \times n}

. При этом в случае, когда верно равенство

U = B E_{r} (a)

, условия (5) удается свести к системе алгебраических уравнений относительно

ψ (0) \in R^{n} {0}

и

α > 0

. Однако эффективность данного подхода снижается в случае несимметричных относительно начала координат множеств

U

, поскольку точность аппроксимации, в роли которой выступает мера Лебега разности двух множеств

μ (U U)

, может оказаться невысокой.

В этой статье предлагается усилить результаты, полученные в [Ибрагимов, 2023а], рассмотрев более общий подход к аппроксимации:

\hat{U} = B (E_{r} (a) + u_{0}), u_{0} \in \int E_{r} (a) . (6)

В частности, необходимо построить эквивалентную условиям (5) систему алгебраических уравнений для частного случая (6), сформулировать основные условия ее разрешимости численно, усилить существующий метод суперэллипсоидальной аппроксимации за счет выбора точки

u_{0}

и исследовать его на оптимальность.

Сведение условий принципа максимума к системе алгебраических уравнений

Покажем, что условия (5) можно свести к эквивалентной системе алгебраических уравнений. Для этого приведем аналитическое описание множеств 0-управляемости и некоторые свойства строго выпуклых и суперэллипсоидальных множеств.

Лемма 1 [9, лемма 1]. Пусть

\det A \neq 0

, класс множеств

{X (N)}_{N = 0}^{\infty}

определяется соотношениями (3). Тогда для любого

N \in N

верно представление

X (N) = - \sum_{k = 1}^{N} A^{- k} U .

Лемма 2 [6, лемма 3]. Пусть

U \subset R^{n}

– строго выпуклый компакт,

0 \in \int U

. Тогда для любых различных

u^{1}, u^{2} \in U

верно

N (u^{1}, U) \cap N (u^{2}, U) = \emptyset .

Также из [6, леммы 5, 6] вытекает следующее утверждение.

Лемма 3. Пусть

U, X \subset R^{n}

– выпуклые компакты,

u \in U

,

x \in X

,

A \in R^{n \times n}

,

\det A \neq 0

.

Тогда

1. $N (u + x, U + X) = N (u, U) \cap N (x, X);$
2. $N (Ax, A X) = {(A^{- 1})}^{T} N (x, X) .$

Лемма 3 определяет преобразование нормального конуса выпуклых множеств при невырожденном линейном преобразовании и сложении по Минковскому. С учетом леммы 1 это позволяет описать произвольный нормальный конус любого множества 0-управляемости в терминах нормальных конусов множества

U

или

E_{r} (a_{1}, \dots, a_{n})

в случае (6). С другой стороны, лемма 2 устанавливает взаимооднозначное соответствие между опорной точкой и ее нормальным конусом для строго выпуклого множества. Если данную зависимость описать в явном виде, то можно получить алгебраические уравнения, эквивалентные условиям (5).

Введем для произвольного

r > 1

биективный оператор

I_{r} : R^{n} \to R^{n}

, действующий по правилу

I_{r} (x) = {(sign (x_{1}) {| x_{1} |}^{r - 1}, \dots, sign (x_{n}) {| x_{n} |}^{r - 1})}^{T} .

Также введем обозначение опорной точки для выпуклого

U \subset R^{n}

и

p \in R^{n} {0}

:

x_{U}^{} (p) = \arg \max_{x \in U} (p, x) .

Теорема 2. Пусть

U \subset R^{n}

– строго выпуклое и компактное множество,

0 \in \int U

,

\det A \neq 0

, класс множеств

{X (N)}_{N = 0}^{\infty}

определяется согласно (3). Тогда условия (5) эквивалентны равенству

\frac{x_{0}}{α} = - \sum_{k = 1}^{N_{\min}} A^{- k} x_{U}^{} ({(A^{- k})}^{T} ψ (0)) .

Доказательство. Поскольку

x_{0} \neq 0

, согласно определению функционала Минковского

α > 0

и верно включение

\frac{x_{0}}{α} \in \partial X (N_{\min})

. С учетом леммы 1 справедливо

\frac{x_{0}}{α} \in \partial (- \sum_{k = 1}^{N_{\min}} A^{- k} U) .

Тогда в силу определения алгебраической суммы множеств найдутся такие

x^{1} \in {- A}^{- 1} U, \dots, x^{N_{\min}} \in {- A}^{- N_{\min}} U

, что

\frac{x_{0}}{α} = \sum_{k = 1}^{N_{\min}} x^{k} .

С учетом пункта 1 леммы 3

- ψ (0) \in N (\frac{x_{0}}{α}, X (N_{\min})) = N (\sum_{k = 1}^{N_{\min}} x^{k}, - \sum_{k = 1}^{N_{\min}} A^{- k} U) = k = 1 N_{\min} N (x^{k}, - A^{- k} U) .

x^{k} = x_{{- A}^{- k} U}^{} (- ψ (0)) = \arg \max_{u \in {- A}^{- k} U} (- ψ (0), u) = {- A}^{- k} \arg \max_{\tilde{u} \in U} (- ψ (0), {- A}^{- k} \tilde{u}) =

- A^{- k} \arg \max_{\tilde{u} \in U} ({(A^{- k})}^{T} ψ (0), \tilde{u}) = - A^{- k} x_{U}^{} ({(A^{- k})}^{T} ψ (0)) .

Таким образом

\frac{x_{0}}{α} = \sum_{k = 1}^{N_{\min}} x^{k} = - \sum_{k = 1}^{N_{\min}} A^{- k} x_{U}^{} ({(A^{- k})}^{T} ψ (0)) .

Теорема 2 полностью доказана.

∎

Частный случай суперэллипсоидальных множеств

Рассмотрим частный случай (6), который характерен тем, что опорную точку для множества

U

можно построить в явном виде.

Лемма 4. Пусть

U \subset R^{n}

– строго выпуклое и компактное множество,

u_{0} \in R^{n}

. Тогда

1) для любого

u \in U + u_{0}

N (u, U + u_{0}) = N (u - u_{0}, U);

2) для любого

p \in R^{n} 0}

существует единственная опорная точка

x_{U + u_{0}}^{} (p) = u_{0} + x_{U}^{} (p) .

Доказательство. Из определения нормального конуса следует пункт 1. Рассмотрим цепочку равенств

x_{U + u_{0}}^{} (p) = \arg \max_{x \in U + u_{0}} (p, x) = \arg \max_{\tilde{x} \in U} (p, \tilde{x} + u_{0}) + u_{0} =

u_{0} + \arg \max_{\tilde{x} \in U} (p, \tilde{x}) = u_{0} + x_{U}^{} (p) .

Пункт 2 доказан.

∎

Учтем известное представление нормального конуса и опорной точки для суперэллипсоидального множества и построим их описание для случая (6).

Лемма 5 [8, лемма 5]. Пусть множество

U = D E_{r} (a)

, где

E_{r} (a)

определяется соотношениями (1),

D \in R^{n \times n}

,

\det A \neq 0

. Тогда

1) для любого

u \in \partial U

N (u, U) = {γ {(D^{- 1})}^{T} diag {(a)}^{- 1} I_{r} (diag {(a)}^{- 1} D^{- 1} u) \in R^{n} : γ > 0};

2) для любого

p \in R^{n} 0}

существует единственная опорная точка

x_{U}^{} (p) = \frac{D diag (a) I_{q} (diag (a) D^{T} p)}{{‖ diag (a) D^{T} p ‖}_{q}^{q - 1}} .

Следствие 1. Пусть

U = D (E_{r} (a) + u_{0})

, где

E_{r} (a)

определяется соотношениями (1),

D \in R^{n \times n}

,

\det A \neq 0

. Тогда

1) для любого

u \in \partial U

N (u, U) = {γ {(D^{- 1})}^{T} diag {(a)}^{- 1} I_{r} (diag {(a)}^{- 1} D^{- 1} (u - u_{0})) \in R^{n} : γ > 0};

2) для любого

p \in R^{n} 0}

существует единственная опорная точка

x_{U}^{} (p) = \frac{D diag (a) I_{q} (diag (a) D^{T} p)}{{‖ diag (a) D^{T} p ‖}_{q}^{q - 1}} + {D u}_{0} .

Доказательство. Согласно определению нормального конуса и лемме 4 пункту 1 выполняется включение

p \in N (u, D (E_{r} (a) + u_{0})) ⟺ D^{T} p \in N (D^{- 1} (u - u_{0}), E_{r} (a)) ⟺

⟺ p \in {(D^{T})}^{- 1} N (D^{- 1} (u - u_{0}), E_{r} (a)) .

Пункт 2 следует из пункта 2 леммы 4 и пункта 2 леммы 5:

x_{U}^{} (p) = \arg \max_{x \in D (E_{r} (a) + u_{0})} (p, x) = \arg \max_{x \in D E_{r} (a) + D u_{0}} (p, x) =

\arg \max_{x \in D E_{r} (a)} (p, x) + {D u}_{0} = \frac{D diag (a) I_{q} (diag (a) D^{T} p)}{{‖ diag (a) D^{T} p ‖}_{q}^{q - 1}} + {D u}_{0} .

Следствие 1 доказано.

∎

Следствие 1 в случае (6) позволяет вычислить оптимальное управление согласно теореме 1 при выборе

D = B

, а в сочетании с теоремой 2 делает возможным свести условия (5) к эквивалентным алгебраическим уравнениям.

Теорема 3. Пусть

U

определяется согласно (6),

x_{0} \neq 0

,

ψ (0) \in R^{n} {0}

,

α > 0

. В таком случае

ψ (0)

и

α

удовлетворяет условиям (5) тогда и только тогда, когда справедливо равенство

\frac{x_{0}}{α} = - \sum_{k = 1}^{N_{\min}} (A^{- k} B u_{0} + \frac{A^{- k} B diag (a) I_{q} (diag (a) B^{T} ({(A^{- k})}^{T} ψ (0)))}{{‖ diag (a) B^{T} ({(A^{- k})}^{T} ψ (0)) ‖}_{q}^{q - 1}}) .

Доказательство. Доказательство теоремы 3 следует непосредственно при подстановке в соотношение, полученное в теореме 2, выражения для опорной точки из пункт 2 следствия 1.

∎

Система уравнений, представленная в теореме 3, имеет не единственное решение, поскольку правая часть инвариантна к домножению вектора

ψ (0)

на любое положительное число. Для использования численных методов можно предположить модификацию данной системы, которая имеет единственное решение.

Следствие 2. Пусть

U

определяется согласно (6),

ψ (0) \in R^{n} {0}

,

α > 0

. Тогда для любого

x_{0} \neq 0

существует единственное решение системы уравнений

{\begin{matrix} - x_{0} = α \sum_{k = 1}^{N_{\min}} \frac{A^{- k} B diag (a) I_{q} (diag (a) {(A^{- k} B)}^{T} ψ (0))}{{‖ diag (a) {(A^{- k} B)}^{T} ψ (0) ‖}_{q}^{q - 1}} + A^{- k} B u_{0}, \\ (ψ (0), ψ (0)) = 1, \end{matrix}

которое также удовлетворяет условиям (5).

Теорема 3 и следствие 2 в совокупности с теоремой 1 позволяют полностью решить задачу быстродействия для линейной дискретной системы в случае суперэллипсоидальной структуры множества допустимых значений управлений (6). Разрешение условий (5) согласно следствию 2 эквивалентно численному решению системы алгебраических уравнений. Одновременно оптимальный процесс и траектория сопряженной системы могут быть вычислены по рекуррентным соотношениям, представленным в теореме 1. Оптимальное управление явным образом определяется пунктом 2 следствия 1.

Внутренняя суперэллипсоидальная аппроксимация выпуклого тела

Результаты [7, 8] расширены на случай, когда множество допустимых значений управлений несимметрично. Имеет смысл рассмотреть сдвиг множества для лучшей аппроксимации, то есть подобрать центр аппроксимирующего множества.

Рассмотрим два различных способа нахождения

u_{0}

– центр масс

u_{01}

и Чебышевский центр

u_{02}

. Так же в работе рассмотрен случай центра суперэллипса в начале координат

u_{00}

.

Центром масс называется геометрическая точка, положение которой определяется распределением массы в теле [4, §10 гл. IV]. Он может быть вычислен путем численного интегрирования:

u_{01} = {(\frac{I_{x_{1}}}{S}, \frac{I_{x_{2}}}{S}, \dots, \frac{I_{x_{n}}}{S})}^{T},

где

I_{x_{i}} = \int_{U}^{❑} x_{i} d x_{1} \dots d x_{n}, i = \bar{1, n}, S = \int_{U}^{❑} d x_{1} \dots d x_{n} .

Чебышевский центр ограниченного выпуклого множества является центром описанного шара минимального радиуса [Гаркави, 1964]. Для случая, когда множество допустимых значений управлений является многогранником, Чебышевский центр является решением следующей задачи оптимизации

x_{0} = \arg \min_{x \in R^{n}} {R > 0 : \max_{u \in U} ‖ x - u ‖ \leq R} .

После определения центра суперэллипсоидального множества и его сдвига, задача сводится к уже рассмотренному в [7, 8].

Рассмотрим примеры субоптимального решения задачи быстродействия с помощью суперэллипсоидальной аппроксимации для нескольких различных систем, где множество

U

является выпуклым несимметричным многогранником. В каждом примере рассматриваются 3 случая – множество с центром в начале координат, со сдвигом на центр масс и со сдвигом на Чебышевский центр.

Пример 1. Для системы с исходными параметрами

A = (\begin{matrix} - 0, 10 & - 1,36 \\ 0,55 & - 0,65 \end{matrix}), U = conv {(\begin{matrix} - 2 \\ - 1 \end{matrix}), (\begin{matrix} 3 \\ - 4 \end{matrix}), (\begin{matrix} 8 \\ - 3 \end{matrix}), (\begin{matrix} 9 \\ 3 \end{matrix}), (\begin{matrix} 6 \\ 7 \end{matrix}), (\begin{matrix} 1 \\ 6 \end{matrix}), (\begin{matrix} - 2 \\ 3 \end{matrix})},

x_{0} = {(10, 30)}^{T}

вычислены центры суперэллипса: центр масс

u_{01} = {(\begin{matrix} 3,59 & 1,40 \end{matrix})}^{T}

и Чебышевский центр

u_{02} = {(\begin{matrix} 3,67 & 1,33 \end{matrix})}^{T}

.

Для 3 случаев центра суперэллипса определены тензоры инерции и вычислены матрицы ориентации суперэллипса:

J_{01} = (\begin{matrix} 815,08 & - 460,15 \\ - 460,15 & 1871,61 \end{matrix}), B_{01} = (\begin{matrix} 0,94 & - 0,35 \\ 0,35 & 0,94 \end{matrix});

J_{01} = (\begin{matrix} 637,74 & - 3,81 \\ - 3,81 & 696,41 \end{matrix}), B_{01} = (\begin{matrix} 0,99 & - 0,06 \\ 0,06 & 0,99 \end{matrix});

J_{02} = (\begin{matrix} 638,10 & - 3,40 \\ - 3,40 & 696,96 \end{matrix}), B_{02} = (\begin{matrix} 0,99 & - 0,05 \\ 0,05 & 0,99 \end{matrix}) .

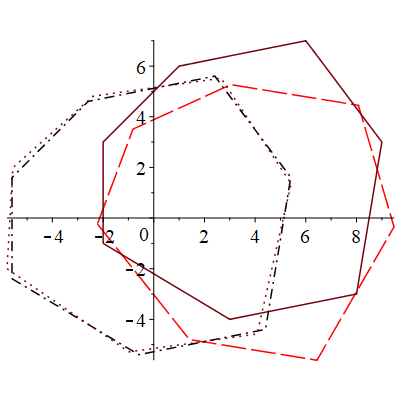
Ориентация множества

U

при разных центрах множества отражена на рис. 1.

Рис. 1. Исходное множество $U$ (непрерывной линией), ориентированное $B^{- 1} (U - u_{00})$ (штриховой линией), ориентированное $B^{- 1} (U - u_{01})$ (штрихпунктирной линией), ориентированное $B^{- 1} (U - u_{02})$ (пунктирной линией)

В качестве аппроксимируемого множества рассматриваются ориентированные многогранники

B^{- 1} (U - u_{0})

:

U_{rot 0} = B^{- 1} (U - u_{00}) =

(\begin{matrix} - 2,22 & 1,41 & 6,44 & 9,48 & 8,07 & 3,04 & - 0,82 \\ - 0,24 & - 4,79 & - 5,61 & - 0,34 & 4,45 & 5,26 & 3,51 \end{matrix});

U_{rot 1} = B^{- 1} (U - u_{01}) =

(\begin{matrix} - 5,74 & - 0,94 & 4,11 & 5,49 & 2,76 & - 2,02 & - 5,34 \\ - 2,02 & - 5,34 & 4,67 & 1,25 & 5,43 & 4,76 & 1,96 \end{matrix});

U_{rot 2} = B^{- 1} (U - u_{02}) =

(\begin{matrix} - 5,79 & - 0,97 & 4,08 & 5,42 & 2,66 & - 2,39 & - 5,56 \\ - 2,00 & - 5,29 & - 4,58 & 1,36 & 5,52 & 4,81 & 1,99 \end{matrix}) .

Рассматриваются следующие значения параметра

r

:

r \in {\frac{6}{5}, \frac{4}{3},2,4,6},

для которых при решении оптимизационных задач были получены оптимальные значения параметров суперэллипсоидальной аппроксимации согласно [7, 8]:

Множество без сдвига:

r = \frac{6}{5}; a_{1}^{} = 2,13; a_{2}^{} = 2,72 .

Множество со сдвигом на центр масс:

r = 2; a_{1}^{} = 5,08; a_{2}^{} = 4, 86.

Множество со сдвигом на Чебышевский центр:

r =;, a_{1}^{} = 4,99; a_{2}^{} = 4,88 .

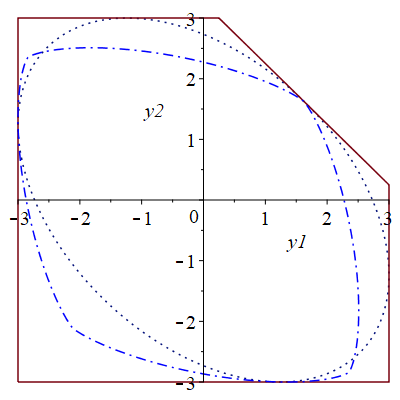
Результаты аппроксимации можно увидеть на рис. 2.

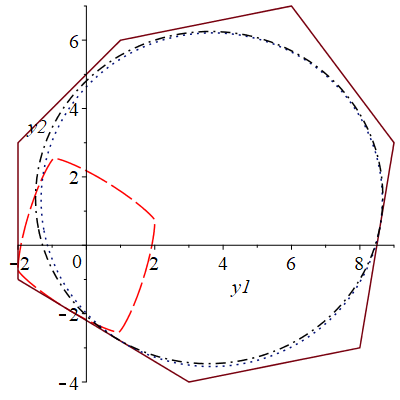
Рис. 2. Исходное множество $U$ (непрерывной линией), ориентированное $B^{- 1} (E_{\frac{6}{5}} (a) - u_{00})$ (штриховой линией), ориентированное $B^{- 1} (E_{2} (a) - u_{01})$ (штрихпунктирной линией), ориентированное $B^{- 1} (E_{2} (a) - u_{02})$ (пунктирной линией)

По рисунку видно, что суперэллипсы со сдвигом в центр масс и Чебышевский центр имеют большую площадь по сравнению с суперэллипсом без сдвига.

В ходе решения системы алгебраических уравнений для вычисления

ψ (0), α

, определенной согласно следствию 2, были получены следующие численные значения параметров:

Множество без сдвига:

α = 0,97; ψ_{01} = 0,05; ψ_{02} = - 0,99; N_{\min} = 9.

Множество со сдвигом на центр масс:

α = 0,95; ψ_{01} = 0,16; ψ_{02} = - 0,99; N_{\min} = 5.

Множество со сдвигом на Чебышевский центр:

α = 0,96; ψ_{01} = 0,17; ψ_{02} = - 0,99; N_{\min} = 5.

Оптимальные траектории, построенные в соответствии с теоремой 2, представлены в табл. 1–4.

Таблица 1. Оптимальная траектория и оптимальное управление для линейной дискретной системы при $N_{\min} = 9$ (множество без сдвига) (k=0…6)

$k$	0	1	2	3	4	5	6
$x^{} (k)$	$10$ $30$	$- 40,007$ $- 13,241$	$21,210$ $- 10,795$	$13,454$ $16,102$	$- 21,438$ $- 2,839$	$5,132$ $- 7,398$	$9,985$ $5,288$
$ψ (k)$	$0,053$ $- 0,998$	$0,630$ $0,214$	$- 0,648$ $1,034$	$- 0,178$ $- 1,221$	$0,965$ $- 0,146$	$- 0,672$ $1,644$	$- 0,569$ $- 1,338$
$u^{} (k)$	$1,928$ $0,722$	$- 0,921$ $2,459$	$0,887$ $- 2,457$	$1,893$ $0,243$	$- 0,921$ $2,459$	$0,416$ $- 2,301$	$1,067$ $- 2,254$

Таблица 2. Оптимальная траектория и оптимальное управление для линейной дискретной системы при $N_{\min} = 9$ (множество без сдвига) (k=7…9)

$k$	7	8	9
$x^{} (k)$	$- 7,162$ $- 0,230$	$0,121$ $- 1,298$	$0$ $0$
$ψ (k)$	$1,357$ $- 0,791$	$- 0,551$ $2,384$	$- 1,165$ $- 1,228$
$u^{} (k)$	$- 0,921$ $2,460$	$- 1,758$ $- 0,906$

Таблица 3. Оптимальная траектория и оптимальное управление для линейной дискретной системы при $N_{\min} = 5$ (множество со сдвигом на центр масс)

$k$	0	1	2	3	4	5
$x^{} (k)$	$10$ $30$	$- 34,590$ $- 9,923$	$17,336$ $- 7,621$	$11,963$ $11,097$	$- 8,158$ $1,378$	$0$ $0$
$ψ (k)$	$0,164$ $- 0,986$	$0,533$ $0,400$	$- 0,695$ $0,847$	$- 0,014$ $- 1,278$	$0,872$ $0,136$	$- 0,788$ $1,452$
$u^{} (k)$	$7,345$ $4,040$	$0,282$ $4,826$	$3,331$ $- 3,294$	$8,195$ $2,035$	$1,049$ $5,343$

Таблица 4. Оптимальная траектория и оптимальное управление для линейной дискретной системы при $N_{\min} = 5$ (множество со сдвигом на Чебышевский центр)

$k$	0	1	2	3	4	5
$x^{} (k)$	$10$ $30$	$- 34,589$ $- 9,884$	$17,431$ $- 7,629$	$12,091$ $11,051$	$- 8,070$ $1,471$	$0$ $0$
$ψ (k)$	$0,166$ $- 0,985$	$0,530$ $0,404$	$- 0,696$ $0,842$	$- 0,010$ $- 1,279$	$0,870$ $0,142$	$- 0,791$ $1,447$
$u^{} (k)$	$7,346$ $4,079$	$0,430$ $4,843$	$3,458$ $- 3,397$	$8,232$ $2,028$	$1,186$ $5,355$

Поскольку множество управлений в случаях с центром масс и с Чебышевским центром шире по сравнению со множеством без сдвига, начала координат удается достигнуть быстрее.

Пример 2. Система имеет следующие исходные данные

A = (\begin{matrix} 2 & 1 \\ 1 & - 1 \end{matrix}), U = conv {(\begin{matrix} 3 \\ 0,25 \end{matrix}), (\begin{matrix} 3 \\ - 3 \end{matrix}), (\begin{matrix} - 3 \\ - 3 \end{matrix}), (\begin{matrix} - 3 \\ 3 \end{matrix}), (\begin{matrix} - 3 \\ 3 \end{matrix}), (\begin{matrix} 0,25 \\ 3 \end{matrix})},

x_{0} = {(- 3, 5)}^{T} .

Вычислен центр суперэллипса – центр масс

u_{01} = {(\begin{matrix} - 0,245 & - 0,245 \end{matrix})}^{T}

, Чебышевский центр в данном случае совпадает с началом координат

u_{00} = u_{02} = {(\begin{matrix} 0 & 0 \end{matrix})}^{T}

.

Тензоры инерции, для которых вычисляются матрицы ориентации суперэллипса, выглядят следующим образом:

J_{01} = (\begin{matrix} 88,06 & 17,55 \\ 17,55 & 88,06 \end{matrix}), B_{01} = (\begin{matrix} 0,71 & 0,71 \\ - 0,71 & 0,71 \end{matrix});

J_{02} = (\begin{matrix} 90,11 & 15,64 \\ 15,64 & 90,11 \end{matrix}), B_{02} = (\begin{matrix} 0,71 & 0,71 \\ - 0,71 & 0,71 \end{matrix}) .

Процедура ориентации множества

U

показана на рис. 3.

Рис. 3. Исходное множество $U$ (непрерывной линией), ориентированное $B^{- 1} (U - u_{01})$ (штрихпунктирной линией), ориентированное $B^{- 1} (U - u_{02})$ (пунктирной линией)

В качестве аппроксимируемого множества рассматриваются ориентированные многогранники

B^{- 1} (U - u_{0})

:

U_{rot 1} = B^{- 1} (U - u_{01}) =

(\begin{matrix} 0 & 4,24 & 1,95 & - 1,95 & - 4,24 \\ - 3,90 & 0,35 & 2,64 & 2,64 & 0,35 \end{matrix});

U_{rot 2} = B^{- 1} (U - u_{02}) =

(\begin{matrix} 0 & 4,24 & 1,95 & - 1,95 & - 4,24 \\ - 4,24 & 0 & 2,30 & 2,20 & 0 \end{matrix}) .

Рассматриваются следующие значения параметра

r

:

r \in {\frac{6}{5}, \frac{4}{3},2,4,6},

для которых при решении оптимизационных задач были получены оптимальные значения параметров суперэллипсоидальной аппроксимации согласно [7, 8]:

Множество со сдвигом на центр масс:

r = \frac{4}{3}; a_{1}^{} = 3,67; a_{2}^{} = 2, 64.

Множество со сдвигом на Чебышевский центр:

r = 2; a_{1}^{} = 3,57; a_{2}^{} = 2, 30.

Результаты аппроксимации можно увидеть на рис. 4.

Рис. 4. Исходное множество $U$ (непрерывной линией), ориентированное $B^{- 1} (E_{\frac{4}{3}} (a) - u_{01})$ (штрихпунктирной линией), ориентированное $B^{- 1} (E_{2} (a) - u_{02})$ (пунктирной линией)

В ходе решения системы алгебраических уравнений для вычисления

ψ (0), α

, определенной согласно следствию 2, были получены следующие численные значения параметров:

Множество со сдвигом на центр масс:

α = 0,98; ψ_{01} = - 0,95; ψ_{02} = 0,31; N_{\min} = 6.

Множество со сдвигом на Чебышевский центр:

α = 0,95; ψ_{01} = 0,99; ψ_{02} = 0,59; N_{\min} = 6.

Оптимальные траектории, построенные в соответствии с теоремой 2, представлены в таблицах 5–6.

Таблица 5. Оптимальная траектория и оптимальное управление для линейной дискретной системы при $N_{\min} = 6$ (множество со сдвигом на центр масс)

$k$	0	1	2	3	4	5	6
$x^{} (k)$	$- 3$ $5$	$0,696$ $- 6,483$	$- 2,620$ $4,764$	$1,077$ $- 5,713$	$- 1,209$ $3,954$	$0,173$ $- 2,675$	$0$ $0$
$ψ (k)$	$0,989$ $0,144$	$0,377$ $0,233$	$0,203$ $- 0,029$	$0,058$ $0,087$	$0,048$ $- 0,039$	$0,003$ $0,042$	$0,015$ $- 0,027$
$u^{} (k)$	$1,696$ $1,516$	$2,469$ $- 2,415$	$1,554$ $1,672$	$2,348$ $- 2,835$	$- 1,362$ $2,488$	$2,328$ $- 2,848$

Таблица 6

Оптимальная траектория и оптимальное управление для линейной дискретной системы при

N_{\min} = 6

(множество со сдвигом на Чебышевский центр)

$k$	0	1	2	3	4	5	6
$x^{} (k)$	$- 3$ $5$	$0,862$ $- 6,809$	$- 2,349$ $5,824$	$0,988$ $- 5,527$	$- 1,248$ $4,040$	$- 0,239$ $- 2,446$	$0$ $0$
$ψ (k)$	$0,998$ $0,058$	$0,352$ $0,293$	$0,215$ $- 0,078$	$0,045$ $0,123$	$0,056$ $- 0,067$	$- 0,003$ $0,063$	$0,020$ $- 0,043$
$u^{} (k)$	$1,862$ $1,190$	$2,735$ $- 1,846$	$- 0,137$ $2,646$	$2,302$ $- 2,475$	$- 1,304$ $2,842$	$1,968$ $- 2,685$

Особых отличий в траекториях нет, однако мера суперэллипса со сдвигом на центр масс больше меры суперэллипса со сдвигом на Чебышевский центр (в данном случае совпадает со множеством без сдвига).

Пример 3. В данном примере рассмотрим наибольший по мере суперэллипс и попробуем решить задачу быстродействия.

Система имеет следующие входные данные

A = (\begin{matrix} - 0,10 & - 1,36 \\ 0,55 & - 0,65 \end{matrix}), U = conv {(\begin{matrix} - 2 \\ - 1 \end{matrix}), (\begin{matrix} 3 \\ - 4 \end{matrix}), (\begin{matrix} 8 \\ - 3 \end{matrix}), (\begin{matrix} 9 \\ 3 \end{matrix}), (\begin{matrix} 6 \\ 7 \end{matrix}), (\begin{matrix} 1 \\ 6 \end{matrix}), (\begin{matrix} - 2 \\ 3 \end{matrix})},

x_{0} = {(10, 30)}^{T} .

Вычислены центры суперэллипса: центр масс

u_{01} = {(\begin{matrix} - 4,08 & - 4,37 \end{matrix})}^{T}

и Чебышевский центр

u_{02} = {(\begin{matrix} - 3,56 & - 3,56 \end{matrix})}^{T}

.

Для 3 случаев центра суперэллипса определены тензоры инерции и вычислены матрицы ориентации суперэллипса:

J_{01} = (\begin{matrix} 1355,27 & - 1173,08 \\ - 1173,08 & 1267,05 \end{matrix}), B_{01} = (\begin{matrix} 0,69 & - 0,72 \\ 0,72 & 0,69 \end{matrix});

J_{01} = (\begin{matrix} 288,10 & - 178,37 \\ - 178,37 & 339,88 \end{matrix}), B_{01} = (\begin{matrix} 0,76 & - 0,65 \\ 0,65 & 0,76 \end{matrix});

J_{02} = (\begin{matrix} 325,50 & - 202,23 \\ - 202,23 & 355,08 \end{matrix}), B_{02} = (\begin{matrix} 0,73 & - 0,68 \\ 0,68 & 0,73 \end{matrix}) .

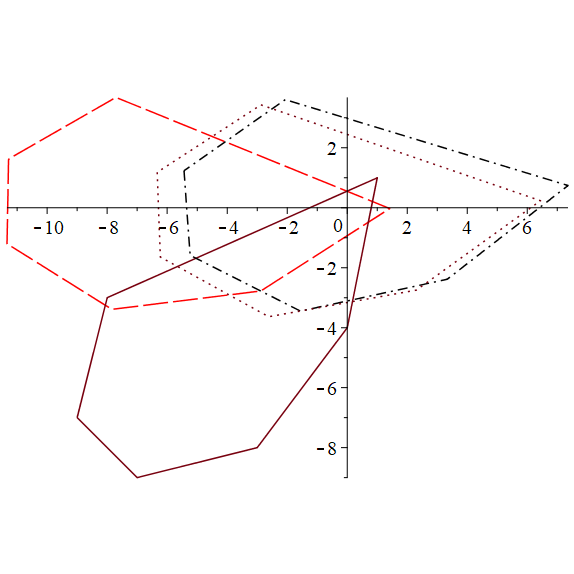
Ориентация множества

U

при разных центрах множества отражена на рис. 5.

Рис. 5. Исходное множество $U$ (непрерывной линией), ориентированное $B^{- 1} (U - u_{00})$ (штриховой линией), ориентированное $B^{- 1} (U - u_{01})$ (штрихпунктирной линией), ориентированное $B^{- 1} (U - u_{02})$ (пунктирной линией)

В качестве аппроксимируемого множества рассматриваются ориентированные многогранники

B^{- 1} (U - u_{0})

:

U_{rot 0} = B^{- 1} (U - u_{00}) =

(\begin{matrix} - 11,28 & - 11,38 & - 7,84 & - 2,88 & 1,41 & - 7,71 \\ 1,62 & - 1,20 & - 3,38 & - 2,77 & - 0,02 & 3,68 \end{matrix});

U_{rot 1} = B^{- 1} (U - u_{01}) =

(\begin{matrix} - 5,44 & - 5,23 & - 1,55 & 3,32 & 7,35 & - 2,06 \\ 1,23 & - 1,58 & - 3,44 & 2,38 & 0,74 & 3,60 \end{matrix});

U_{rot 2} = B^{- 1} (U - u_{02}) =

(\begin{matrix} - 6,33 & - 6,22 & - 2,61 & 2,30 & 6,43 & - 2,87 \\ 1,18 & - 1,64 & - 3,63 & - 2,74 & 0,23 & 3,43 \end{matrix}) .

Рассматриваются следующие значения параметра

r

:

r \in {\frac{6}{5}, \frac{4}{3},2,4,6},

для которых при решении оптимизационных задач были получены оптимальные значения параметров суперэллипсоидальной аппроксимации согласно [7, 8]:

Множество без сдвига:

r = \frac{6}{5}; a_{1}^{} = 1,20; a_{2}^{} = 0,48 .

Множество со сдвигом на центр масс:

r = 2; a_{1}^{} = 5,34; a_{2}^{} = 2, 49.

Множество со сдвигом на Чебышевский центр:

r = \frac{6}{5}; a_{1}^{} = 6,09; a_{2}^{} = 2,25 .

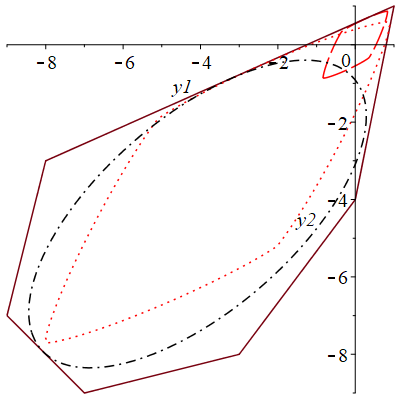
Результаты аппроксимации можно увидеть на рис. 6.

Рис. 6. Исходное множество $U$ (непрерывной линией), ориентированное $B^{- 1} (E_{\frac{6}{5}} (a) - u_{00})$ (штриховой линией), ориентированное $B^{- 1} (E_{2} (a) - u_{01})$ (штрихпунктирной линией), ориентированное $B^{- 1} (E_{2} (a) - u_{02})$ (пунктирной линией)

По рисунку видно, что суперэллипсы со сдвигом в центр масс и Чебышевский центр имеют большую площадь по сравнению с суперэллипсом без сдвига. Однако можно заметить, что суперэллипс со сдвигом на центр масс, имеющий наибольшую меру, не включает начало координат, соответственно нарушается условие

0 \in \int U

, решение задачи быстродействия не может быть вычислено.

Заключение

В разделе 2 введены обозначения для дальнейшей работы. В разделе 3 описана постановка задачи быстродействия и задачи аппроксимации. В разделе 4 рассматривается приведение сложноразрешаемых условий из принципа максимума к суперэллипсоидальной структуре ограничений, которую можно разрешить аналитически. В разделе 5 представлена внутренняя суперэллипсоидальная аппроксимация выпуклого тела, в частности рассмотрен случай несимметричным множеств, для которых требуется определить центр аппроксимирующего множества. В разделе 6 приведены примеры решения задачи быстродействия на основе доказанных утверждений для разных систем со сравнением результатов для различных центров суперэллипса.

Представленные в статье методы могут применяться для численного моделирования и симуляции динамики разнообразных естественных и технических систем. За счет простоты построения оптимальных процессов на основе принципа максимума и формирования программного управления, удается не только решить задачу быстродействия для заданного начального состояния, но и собрать большой объем модельных данных и различных траекторий для дальнейшего анализа системы. В то же время, аппарат суперэллипсоидальных аппроксимаций гарантирует более высокую точность по сравнению с классическими эллипсоидальными методами аппроксимации.

О субоптимальном решении задачи быстродействия для линейной дискретной системы в случае несимметричных ограничений на управления

Резюме

Общая информация

Полный текст

Введение

Обозначения

Сведение условий принципа максимума к системе алгебраических уравнений

Заключение

Литература

Информация об авторах

Метрики

Просмотров web

Скачиваний PDF

Всего