ВВЕДЕНИЕ
Проблема повышения качества математического образования в начальной школе остается одной из наиболее актуальных в современной педагогической науке и практике. Начальный этап обучения закладывает основы математической грамотности и математического мышления, от которых во многом зависит дальнейшая академическая успешность учащихся. Однако практика показывает, что значительная часть младших школьников испытывает трудности при освоении курсов математики [Mangarin]. Многие ученики допускают систематические математические ошибки, теряя интерес к предмету, что негативно сказывается на качестве дальнейшего естественнонаучного образования [Václavíková]. Одной из причин подобных затруднений является ограниченная возможность учителя в условиях классно-урочной системы выявлять индивидуальные ошибки каждого ученика и своевременно работать над их устранением. Как отмечает В.Л. Соколов, учителям начальных классов зачастую не хватает времени и навыков для детального анализа и обсуждения ошибок учеников во время уроков [Соколов]. В результате многие ошибки остаются непроработанными, закрепляются в мышлении учащихся и приводят к возникновению стойких неправильных представлений о математических понятиях [Kusmaryono].
Описанная в данной работе информационная система призвана помочь учителям решить проблемы, затрудняющие организацию индивидуализации обучения, за счёт адаптивного подхода к оценке сложности предъявляемых заданий и системе подсказок, ориентирующейся на типы ошибок, совершаемых учащимися в процессе решения предъявляемых задач курса математики начальной школы. Диагностика ошибок в данной системе подразумевает классификацию ответов ученика в терминах известного множества типовых ошибок. Здесь система опирается на реестр ошибок - базу знаний, в которой описаны распространенные ошибки при выполнении каждого вида заданий. Каждому неправильному ответу (или характеру решения) сопоставляется определённая причина ошибки. Разрабатываемая система предназначена для формирования и развития математических навыков у младших школьников через индивидуализированную работу над ошибками. В процессе работы с данной информационной системой учащийся проходит пары состояний. В каждой из пар состояний учащемуся предъявляется задание и четыре варианта ответов, из которых верным всегда является только один. В случае, если учащийся дает один из трех ошибочных ответов, он попадает в состояние «ловушки», где ему предъявляется та же самая задача, но с подсказкой. Подсказка представляет собой либо некоторый наводящий вопрос, ответив на который ученик может прийти к верному решению, либо некоторую теоретическую информацию, которая помогает учащемуся решить данную задачу. После успешного решения задачи учащемуся предъявляется следующее задание из следующей пары состояний. Каждая следующая пара состояний содержит более сложные задачи. Банк заданий сформирован таким образом: все задания поделены на четыре большие группы, каждая группа для одного из четырёх классов. В каждом классе рассматриваются три крупные темы, и, в каждой теме три категории заданий: легкие, средней сложности и повышенной сложности. Таким образом, в каждом классе есть девять категорий заданий и, в обучающей системе эти девять категорий представлены девятью парами состояний марковской модели.
СОВРЕМЕННЫЕ АДАПТИВНЫЕ СИСТЕМЫ В НАЧАЛЬНОМ ОБРАЗОВАНИИ И АРХИТЕКТУРА ПРЕДЛАГАЕМОГО РЕШЕНИЯ
Индивидуализация обучения и своевременные решения учебных затруднений рассматриваются в педагогической науке как важнейшие условия повышения эффективности образования [Dias]. В мировой практике накоплен положительный опыт использования адаптивных цифровых ресурсов в начальном образовании. Так, в исследовании Х. Дж. Банг показал, что использование игровой адаптивной системы «My Math Academy» для учеников 1-2 классов привело к значимому росту результатов по математике по сравнению с контрольной группой и особенно высокую эффективность адаптивное обучение продемонстрировало у учащихся с низким исходным уровнем подготовки, благодаря возможности подстраивать сложность заданий под индивидуальные потребности ребенка [Bang]. В современных работах, направленных на исследования индивидуализации обучения, подчёркивается, что применение технологий, обеспечивающих индивидуальный темп и траекторию обучения, позволяет учителю эффективнее работать с классом, где у детей разный уровень знаний [7, 8]. Цифровые платформы адаптивного обучения, встроенные в учебный процесс, могут снизить нагрузку на учителя, взяв на себя часть функций по мониторингу успехов учащихся и подбору заданий соответствующего уровня сложности.
В России ведутся исследования в области адаптивного обучения математике. В частности, под руководством Л. С. Куравского и соавторов разработана концепция адаптивного учебного тренажёра, основанного на использовании марковских моделей для постепенного усложнения заданий в зависимости от успехов учащихся [Куравский]. Данный подход позволяет учитывать динамику процесса обучения и снижать число необходимых заданий для достижения запланированного результата.
Задача преодоления учебных ошибок младших школьников на уроках математики может решаться благодаря разработке методов работы над ошибками [Иванова, 2019]. Например, классифицировать типы детских ошибок и выявлять стоящие за ними ошибочные представления для адресной коррекции [Ashlock]. Так, В.Л. Соколов выделяет распространенные типы ошибок на примере темы «Вычитание» и описывает приёмы педагогической работы по их устранению, включая организацию специального обсуждения ошибок в классе и использование наглядных моделей [Kusmaryono]. Однако внедрение таких методов в массовой школе затруднено из-за ограниченности учебного времени и больших классов. Поэтому автоматизация процесса выявления и разбора ошибок с помощью современных информационных систем является актуальной научно-практической задачей.
Архитектура системы построена на концепции структурных единиц, каждая из которых включает три ключевых компонента: банк заданий, реестр возможных ошибок и банк средств для их преодоления. Структурная единица системы рисунке 1 имеет номер 2.1.1.

Это означает первую группу заданий первой темы для второго класса. Данный функциональный блок, обеспечивает реализацию адаптивного обучения в рамках конкретной тематической области. Банк заданий содержит математические задачи трёх уровней сложности с предусмотренными вариантами ответов. К каждому заданию прилагается четыре варианта ответа: один правильный и три неправильных, отражающих типичные ошибки учащихся.
Реестр возможных ошибок содержит структурированную классификацию ошибок, характерных для данной группы заданий. Для каждой типичной ошибки указывается её название, содержательное описание и примеры проявления. Например, в теме вычитания двузначных чисел выделяются такие типы ошибок как «концептуальная ошибка – непонимание значений разрядов числа» и «ошибки в знании таблицы сложения». Это позволяет системе не только фиксировать неверные ответы, но и диагностировать их причины.
Банк средств для преодоления ошибок представляет собой набор подсказок, каждая из которых направлена на преодоление конкретного типа ошибки. Подсказки разрабатывались с учетом педагогических принципов включают текстовые пояснения, помогающие школьнику понять и исправить допущенную ошибку. Например, при ошибке в понимании разрядов числа учащемуся демонстрируется наглядное представление числа с выделением десятков и единиц.
Такая архитектура позволяет системе гибко реагировать на действия ученика, предоставляя ему индивидуализированную поддержку в процессе обучения. При неверном ответе система не просто сообщает о его неправильности, но определяет тип ошибки и предоставляет соответствующую подсказку, направленную на осознание и исправление конкретного заблуждения.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБУЧАЮЩЕГО ПРОЦЕССА
Математической основой системы является марковский процесс с дискретными состояниями и непрерывным временем [Артеменков]. Эта модель позволяет описывать динамику взаимодействия ученика с системой, представляя процесс выполнения заданий как последовательность переходов между различными состояниями (рис. 2).

Рис. 2. Марковский процесс с дискретными состояниями и непрерывным временем
Где и - состояния процесса,
- интенсивности переходов между состояниями.
Каждое состояние характеризуется определенным уровнем сложности заданий и типом необходимой поддержки (определёнными подсказками в случае неверного ответа). Согласно работам Л.С. Куравского [13, 14] вероятности пребывания в состояниях процесса, как функции времени, определяются следующей системой обыкновенных дифференциальных уравнений Колмогорова в матричной форме:

Где (T – конечный момент времени),
– вероятности пребывания в состояниях процесса,
– матрица интенсивностей переходов между состояниями порядка . Переходы между состояниями определяются результатами выполнения заданий.
В контексте начального курса математики под состояниями понимаются уровни овладения определёнными тематическими умениями и понятиями. Например, отдельные состояния могут соответствовать базовому пониманию сложения, уверенным навыкам вычитания без перехода через разряд, продвинутому владению операциями с двузначными числами и т.д. Решение каждой учебной задачи трактуется как событие, приводящее либо к переходу ученика в новое состояние (при успешном решении), либо к повторному предъявлению задания текущего состояния (попалание в «ловушку»). Таким образом, траектория обучения ученика описывается последовательностью состояний где случайность переходов обусловлена как верными, так и неверными действиями ученика.
Формально, для каждого состояния существует набор допустимых задач определённого содержания и уровня сложности, а также набор подсказок или разъяснений, которые могут быть предоставлены ученику. Если ученик справляется с задачей, система переводит его в состояние более высокого уровня сложности или продвигает дальше в рамках текущей темы. Если же ученик ошибается, система может перевести его в состояние «ловушки», в котором будет представлена та же самая задача с подсказкой для устранения конкретной ошибки. Подсказки представляют собой заранее заготовленные объяснения или наводящие вопросы, связанные с типом ошибки, например, напоминание о правилах вычитания с переходом через разряд.
Определение значений свободных параметров марковской цепи осуществляется путем сравнения наблюдаемых и прогнозируемых распределений частот пребывания в состояниях модели. Для этого определяется набор интенсивностей, обеспечивающий наименьшее значение статистики Пирсона:
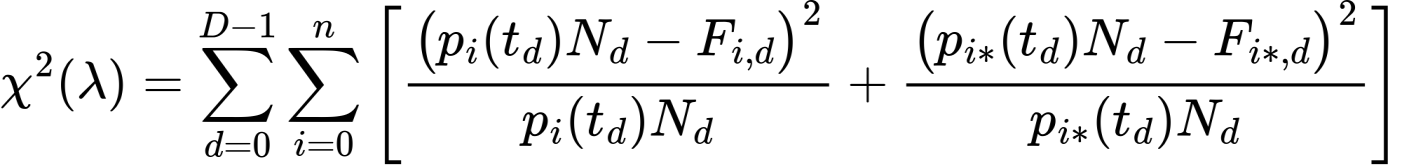
где , , – наблюдаемые частоты пребывания в состояниях процесса в моменты времени .
Данная статистика представляет собой меру согласования применяемой математической модели с наблюдениями.
Важным преимуществом выбранного теоретического подхода является его интерпретируемость. Система не использует непрозрачные «чёрные ящики» вроде сложных нейронных сетей — все её решения (оценки, переходы, подбор подсказок) основаны на понятных педагогам правилах и статистических закономерностях, которые поддаются содержательному объяснению. Благодаря этому система легко интегрируется в реальный учебный процесс.
ПРОГРАММНАЯ РЕАЛИЗАЦИЯ АДАПТИВНОЙ ЦИФРОВОЙ СИСТЕМЫ
Программная реализация адаптивной цифровой системы состоит из серверной и интерфейсной части веб-приложения.
Серверная часть использует веб-фреймворк CakePHP с дополнительными модулями для обеспечения функционала аутентификации и авторизации пользователей. Фреймворк обладает всем необходимым функционалам для быстрого построения веб-приложений реализуя паттерн «Модель-Вид-Контроллер». Для написания цифровой системы используется язык программирования PHP версии 8.2.1.
Интерфейсная часть задействует фреймворк Bootstrap для построения адаптивного интерфейса веб-приложения и формирования его мобильной версии. Для визуализации значков интерфейса используется масштабируемые векторные иконки от Font Awesome. Заполнение и загрузка файлов в текстовые поля ввода происходит с помощью кроссплатформенного JavaScript HTML WYSIWYG редактора TinyMCE.
Для развертывания тренажера был задействован сервер с операционной системой Debian и веб-сервер Nginx. В качестве базы данных был задействован PostgreSQL.
- ВЗАИМОДЕЙСТВИЕ РЕДАКТОРОВ И ПОЛЬЗОВАТЕЛЕЙ С АДАПТИВНОЙ ЦИФРОВОЙ СИСТЕМОЙ
Наполнение адаптивной цифровой системы материалами происходит с помощью административной панели веб-приложения. Доступом к ней обладают пользователи с правами администратора, редактора или учителя. Осуществляется разделение прав разный ролей системы посредством файлов политики. Доступ к особо важным компонентам веб-приложения разрешается только редакторам и администраторам. Формирования пар марковского процесса и их последовательности доступно после заполнения следующих сведений: основное описание тренажера, список субтестов (аналог групп заданий, связанных одной логикой), банка заданий, реестра возможных ошибок с подсказками для них. После ввода этих сведений создается отдельная последовательность пар состояний и осуществляется их связывание с определённым субтестом. Для каждой пары состояний возможно подключение только одной группы заданий.

На рисунке 3 изображен фрагмент формы заполнения используя, которую пользователь может добавить новое задание в систему если обладает необходимым доступом к странице. С помощью редактора доступна возможность загрузки файлов изображения для наглядного представления заданий пользователю. Также это позволяет более информативно предоставить подсказки, которые предъявляются в состояниях «ловушках» для избегания использования большого количества текста. Использование готовых вариантов ответа на задание позволяет упростить логику системы и сделать её более доступной для учителей. Составление неверных вариантов ответов осуществляется на основе самых распространённых ошибок, которые школьник может допустить при решение выбранной группы задач. Готовые варианты ответа в данной системе предоставляют оптимальный компромисс между сложностью системы и потребностью учителей. Также некоторые задания требуют ответа символами, которые не представлены на клавиатуре, а использование его виртуального варианта сильно усложняет взаимодействие с системой школьника начальных классов. Использование пользовательского ввода при решении задач негативно сказывается на взаимодействие учителей с веб-приложением из-за необходимости составления правил для связывания большого количества вариантов ответа пользователя с определенными ошибками. Готовые варианты ответа лишены данного недостатка так как используют логику, один вариант ответа связывается с одной ошибкой.

На рисунке 4 представлена схема марковского процесса тренажера для поддержки учебного процесса при изучении тем учебного предмета «Математика» второго класса начальной школы. Школьник начинает в «Состояние 1», которая отмечена зеленым цветом. К данному состоянию подключена первая структурная единица, являющаяся абстракцией для хранения банка заданий, реестра ошибок и подсказок. Первая пара состояний предлагает решить простое задание без звездочки из первой темы для второго класса. Нумерация элементов абстракции следующая: первое число – номер класса, второе число – номер темы, третье число – номер группы заданий, четвертое число – номер задания. Пример 3.1.2.4 – это четвертое задание из второй группы заданий первой темы для третьего класса.

При входе в первую пару состояний пользователю случайно предлагается задача из первой группы заданий. Пользователю предоставляется текст задачи и готовые варианты ответа, которые он может выбрать. Выбор неверного ответа в задаче приводит пользователя в состояние «ловушки». В нем пользователь получает идентичное задание с подсказкой по её решению. Каждый неверный вариант ответа связан с определенной распространённой для этого задания ошибкой. При выборе ответа происходит запись результатов в базу данных.

Результаты содержат необходимую информацию о переходах пользователя по парам состояний марковского процесса. Также представлена информация о выпавшем пользователю задании и выбранным им готовым вариантом ответа. При неверном ответе записывается ошибка, которую он допустил в этой задачи. В рамках системы пользователь может совершить пять действий. Вход в ловушку обозначает переход в состояние «ловушки» из обычного состояния при выборе неверного ответа в нём. Нахождение в ловушки срабатывает при повторном выборе неверного ответа при нахождении в состоянии «ловушки». Если пользователь даёт правильный ответ на задачу в состоянии «ловушки», то он переходит в обычное состояние и получает новое задание. При выборе правильного ответа в обычном состоянии осуществляется переход в новую пару состояний марковского процесса. Если пользователь находится в последней паре состояний и не находится в ловушке при выборе правильного ответа происходит завершение тренажера. Для успешного прохождение тренажера пользователю нужно пройти все состояния марковского процесса и успеть во временные рамки, установленные для него системой. Итоговые результаты школьников визуализируется в личном кабинете учителя.
ЗАКЛЮЧЕНИЕ
Представленная цифровая система является современным примером использования технологий искусственного интеллекта в образовании начальных классов. Её применение способно обеспечить адресную помощь каждому ученику, повысить уровень усвоения математических знаний, мотивацию и интерес к предмету. В то же время, система предоставляет учителям эффективный инструмент для индивидуализации учебного процесса и своевременного выявления ошибок, что способствует более глубокому и качественному обучению в условиях массового образования.
Планируемые этапы апробации системы включают проведение экспериментальных исследований в реальных школьных условиях с целью оценки её педагогической эффективности и удобства использования. Ожидается, что внедрение данной системы позволит повысить успешность освоения математического материала младшими школьниками, а также снизить нагрузку на учителя за счёт автоматизации диагностики и коррекции учебных затруднений.
Перспективы дальнейшего развития проекта связаны с расширением банка заданий и реестра типичных ошибок, интеграцией дополнительных форм поддержки обучающихся, а также адаптацией системы под другие предметные области и возрастные категории. Кроме того, возможна реализация аналитических модулей для глубокого анализа траекторий обучения и индивидуального прогноза успешности, что откроет новые возможности для персонализированного подхода в образовании.
Таким образом, разработанная система представляет собой важный шаг на пути цифровой трансформации образовательного процесса, способствуя повышению качества и доступности школьного образования.