Некоторые особенности формирования действия моделирования при обучении математике детей шести лет

Исследование направлено на изучение техники введения действия моделирования с учетом возрастных особенностей шестилеток. Автор доказывает, что абстрактная символика принимается шестилетками легко и быстро и может быть введена на ранних этапах обучения. Абстрактная символика позволяет детям решить задачи, нацеленные на обобщение учебного материала в форме конкретных заданий.

В настоящее время в некоторых школах пытаются вводить развивающее обучение по системе Эльконина – Давыдова для детей шести лет. Прямой перенос программы по математике, разработанной для семилетних, может вызвать у младших детей серьезные затруднения. Поэтому для шестилеток нужна специальная программа. Цель настоящей статьи – заострить внимание педагогов на технике введения действия моделирования с учетом возрастных особенностей шестилеток, которую мы использовали в нашем курсе математики. Заметим, что в этом курсе понятие числа строится, как и в общепринятой программе, на основе действия счета, но и при смене единиц счета.

Следует подчеркнуть, что действие моделирования – это не «дополнительная тема» в обучении, а средство перевода мышления учащихся на более высокий уровень, средство, позволяющее в значительной мере избежать формализма знаний. Обучая ребенка способу построения модели некоторого явления, а затем способу работы с моделью, учитель осуществляет процесс формирования в его сознании соответствующих абстракций, подводит его к обобщению.

Освоение действия моделирования начинается с замещения конкретных предметов условными объектами, позволяющими наглядно выделить искомое отношение. Далее, выполнение определенных действий с такого рода заместителями приводит к обнаружению свойств отношения. Наконец, результаты этих действий интерпретируются на языке конкретных вещей и явлений, что и является конечной целью всей этой работы.

Учащиеся выполняют задания на замещение реальных объектов с самого начала обучения. Конкретные предметы замещаются условными фишками или геометрическими фигурами, а вместо реальных действий с предметами выполняются условные движения. К заданиям такого рода учителю следует относиться внимательно и четко соблюдать логику действий.

Допустим, на доске изображены в ряд 4 белки и 3 зайца. Дети хором пересчитывают «всех зверьков». Потом на парты они кладут столько же квадратов. Затем пересчитывают только белок. Под квадратами кладут 4 треугольника. Учитель предлагает ученикам: «Охватите руками фигуры, которые заменяют белок. (Дети заключают между указательными пальцами правой и левой руки 4 треугольника.) Охватите фигуры, заменяющие всех зверей (показывают тем же жестом 7 кругов). Одинаково ли на доске белок и всех зверьков! Ответ на этот вопрос для многих шестилеток не очевиден, так как у них еще не сформировалось понятия об отношении целого и части. Некоторые могут сказать, что белок больше, чем зверьков, имея в виду под зверьками зайцев. Тут и нужно обратить внимание учеников на отношения между знаковыми заместителями объектов. Ученики движением своих рук уже обозначили множество зверьков и подмножество белок, но пока этого еще не осознали. Учитель может вновь предложить ученикам охватить руками фигурки, заменяющие сначала всех зверьков, а затем белок, и оценить, сузили они или расширили размах рук. Конечно, дети скажут, что сузили. «Значит, чего больше: фигурок, заменяющих зверьков или белок?» Дети ответят, что фигур про зверьков больше. «Значит, и зверьков больше, чем белок. Давайте проверим. Посмотрите на доску. Охватите руками всех зверьков. Запомните положение рук. А теперь охватите руками всех белок. Положение рук сузилось? Значит, зверьков больше, потому что белки – это только часть зверей».

Обычно сравнение целого и его большей части представляет серьезную трудность для детей шести лет, если не производить описанного предварительного действия замещения. Полного преодоления затруднения не произойдет, однако указанные упражнения важны для освоения действия замещения одних объектов другими и для того, чтобы дети почувствовали различие части и всего целого.

Для закрепления на доску выставляются 7 ромашек и 3 колокольчика. Нужно определить, чего больше – ромашек или цветов? Дети действуют с фигурами-заменителями так же, как и в предыдущем задании.

Третье задание учащиеся выполняют с большей долей самостоятельности. На доске 3 подосиновика и 1 мухомор. Учащиеся выкладывают круги, замещающие все грибы, а под ними квадраты, замещающие подосиновики. Может быть, кто-то из детей сможет «угадать» ответ на вопрос, заданный учителем («Одинаково ли всех грибов и подосиновиков?»). Обосновывая ответ, дети должны показать жестом (не называя чисел) фигуры, замещающие все грибы, фигуры, замещающие подосиновики. Есть лишние круги, а квадратов не хватает, значит, грибов больше, чем подосиновиков, а подосиновиков меньше, чем грибов.

Средствами моделирования выступают также абстрактная символика и так называемые «чертежи». Как это ни покажется невероятным для сторонников традицией-ной методики, абстрактная символика принимается шестилетками легко и может быть введена на ранних этапах обучения, ее появление позволяет затем ставить перед детьми задачи, нацеленные на обобщение учебного материала в форме конкретных заданий. Выполнить такие задания возможно только при актуализации принципа действия. Так, например, работая с рядом «сказочных цифр», учащиеся осваивают общую идею порядка и принцип ее использования при выполнении вычислений.

Сначала дети отрабатывают действия со знакомыми им числами. На доске 4 перевернутые карточки с цифрами. Учитель сообщает, что здесь числа стоят по порядку. «Покажите самое маленькое! (Дети должны показать левую карточку, не переворачивая ее.) Покажите число на 1 больше... Покажите самое большое из этих чисел... Теперь на 1 меньше... Но что это за числа? (Открывается средняя карточка там 7.) Назовите число на 1 меньше... Откройте нужную карточку... Какое число на 1 больше, чем 7?.. Откройте нужную карточку... (Все предположения проверяются переворачиванием карточки с цифрой.)»

После этого вводится сказочный сюжет. «К нам в школу в гости, когда вас не было, приходила Красная Шапочка. Она учится в сказочной школе и принесла карточки со сказочными цифрами. У них в сказочной школе числа стоят по порядку, как у нас». Выставляются 5 перевернутых карточек. Детям предлагается указать (не переворачивая карточку) самое большое число, число на 1 меньше, самое маленькое число и на 1 больше. Наконец, средняя карточка открывается и обнаруживается неизвестный знак: Ω. Учитель не удивляется: «В сказочной школе цифры пишутся по-другому. А можно догадаться, что это за число?» Дети решат, что это 3, так как оно третье от края. Учитель возражает: «Красная Шапочка говорила, что захватила с собой числа не с самого начала ряда. Она не хотела раскрывать секрета. Но предложила посмотреть, как пишется число, которое на 1 меньше, чем открытое». Дети должны догадаться, что нужно перевернуть предыдущую карточку. А еще на 1 меньше?.. А на 1 больше? и т. п.

Подчеркивается, что хотя мы не знаем, что это за числа, но смогли догадаться, какое из них самое маленькое, самое большое. (Пример знаков в ряду: Δ Λ Ω * L γ).

Задания с абстрактной символикой присутствуют почти на каждом уроке. Они становятся, на наш взгляд, средством развития мышления ребенка, поскольку, с одной стороны, требуют от него обобщения, а с другой – создают условия для его осуществления. Действительно, маленькие школьники часто не в состоянии прийти к общему способу действия при решении задач, потому что, работая с конкретными числами, могут получить ответ не на основе анализа отношений, заложенных в условии задачи, а манипулируя числами. Этой возможности им трудно противостоять. Оказывается, что замена в условии задач чисел первого десятка «сказочными цифрами» мобилизует мышление ребенка. Конечно, в определенных случаях этой мобилизации недостаточно, и тогда для формирования обобщения требуется прибегнуть к использованию других средств моделирования, в частности к пространственно-графическим построениям – «чертежам». Так, именно работа с чертежами позволяет учащимся выявить и усвоить свойства отношения целого и частей. В результате этой работы им становятся доступными для решения текстовые задачи, обычно считающиеся трудными и для детей восьми лет.

Следует отметить, что введение «чертежей» – процесс более тонкий, чем введение абстрактной символики. Многие задания с абстрактной символикой могут быть использованы даже при работе по традиционным учебникам. Однако, если учитель вдруг начнет объяснять способ решения задач с помощью чертежей, это не только не даст положительного эффекта, но может создать дополнительные трудности.

При обучении шестилетних учеников работа по введению чертежа начинается с того, что предметные совокупности, о которых шла речь в задаче, загораживаются большими фишками, которые пространственно совмещаются так, чтобы сделать наглядными определенные особенности изучаемого отношения. Потом фишки замещаются их изображениями – вычерченными прямоугольниками. При этом особым образом выделяются и обозначаются элементы полученного чертежа. В дальнейшем выполнение чертежа становится для учеников материальной формой анализа математического содержания конкретных предметных ситуаций, текстовых арифметических задач.

Продемонстрируем, как может быть введена пространственная модель целого и частей. Сначала дети отрабатывают выделение целого и частей в предметных ситуациях. Например, сообщается сюжет: «Сестра принесла домой 5 грибов (выставляются на доску), брат – 4 гриба (выставляются). Мама посчитала все грибы – их оказалось 9». На доске пишутся З числа: 5, 4, 9. Вызываются 3 ученика – «хозяева» этих чисел. Каждый из детей должен взять в руки свою кучку грибов. Обнаруживается, что два человека могут взять грибы (5 и 4), а третьему ничего не достается!.. Грибы ставятся на место. Учитель предлагает взять грибы сначала третьему ученику, а потом двум другим. В этом случае без грибов оказываются двое... Где же их грибы? – Они у третьего ученика. Учитель подсказывает подходящие слова: «У третьего все грибы, общее их число, а у двух детей – части».

Когда дети начинают ориентироваться в таких ситуациях, вводятся фишки – заместители предметных совокупностей. Например, на доске 8 яблок, у детей 6 кругов. «У мамы было 8 яблок. Из них 3 оказались кислыми, остальные 5 – сладкими...» Выделяются соответствующие части. Сколько получилось частей? – Две. – Покажите одну часть... другую... общее число яблок...

Три ученика у доски должны теперь не взять свои яблоки, а закрыть их фишкой.

Одной фишкой закрывается часть 5, другой – часть 3 (чтобы фишка закрывала картинки, они сдвигаются стопками). Все яблоки закрыты, но есть еще число 8 и одна фишка... Где находятся нужные яблоки?.. Делается охватывающий жест, и фишка накладывается на прежние две. Те же действия ученики проделывают потом за партами.

Когда дети освоят эти действия, им раздаются заготовки чертежей в виде прямоугольников и сообщается следующее: «Буратино прислал рассказ и просил сделать на листочке рисунок, из которого было бы понятно, что в рассказе части, а что общее число». Учитель выставляет (пачками) изображения цветов: «В вазе было 14 красных тюльпанов – закроем их фишкой... Но у вас нет картинок и фишек, а есть начерченный прямоугольник. Представим себе, что он загораживает (как фишка) 14 тюльпанов... В вазе были еще 13 желтых тюльпанов... Закроем их новой фишкой». Выясняется, что детям нужно пририсовать второй прямоугольник... Учитель продолжает: «Всего же тюльпанов было 27. Покажите их на картинках и на чертеже. (Дети охватывают руками обе части.) Я ставлю новую фишку, а как быть вам? (Можно все обвести.) А может быть, нужно нарисовать рядом еще один прямоугольник? (Нет, тогда получится 3 части.)» Вызываются 3 ученика, чтобы взять в руки 14, 13 и 27 цветов. «Коля, покажи на фишках и чертеже, где «спрятаны» твои 14 тюльпанов. (Делает охватывающие жесты.) Пометим это на чертеже так: нарисуем Колю и Колины руки (рисуется дуга). Коля нам говорит: «Здесь 14 тюльпанов», – запишем это». Таким же образом обозначаются дугой и числом остальные элементы чертежа, так что он принимает следующий вид:

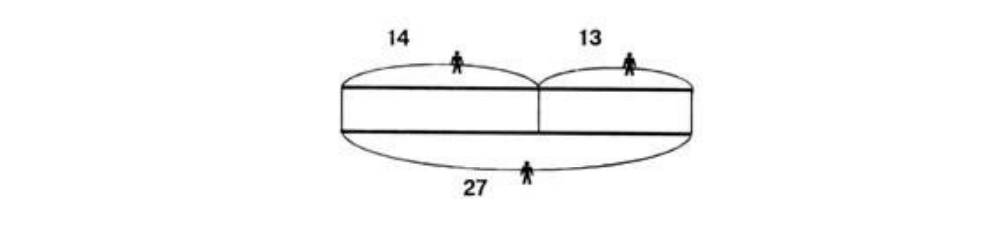
(Без ссылки на «руки» и «голову» дети с трудом воспринимают значение дуг, которые все же нужны для точного соотнесения чисел и элементов схемы. В дальнейшем необходимость рисования человечков отпадает.) Вызванные к доске ученики пытаются взять в руки «свои» цветы. Устанавливается, что 27 состоит из двух частей. Подчеркивается, что это хорошо видно по чертежу.

При выполнении чертежей нужно варьировать их несущественные моменты. Так, целое следует помечать дугой то сверху, то снизу, а части нужно пририсовывать или выделять то слева, то справа.

В дальнейшем выполнение чертежа становится для учеников материальной формой анализа математического содержания текстовых арифметических задач. Но и в этот период нужно время от времени напоминать учащимся «происхождение чертежа» – он замещает фишки, за которыми, в свою очередь, скрываются некоторые предметные совокупности.

1. Давыдов В.В., Горбов С.Ф., Микулина Г.Г., Савельева О.В. Обучение математике. I класс. М., 1994.
2. Микулина Г.Г. Учимся понимать математику. I класс (I—IV). М., 1995.