О способах обучения младших подростков математике в форме квазииследовательской деятельности

Автор изучал реальные возможности развития теоретического мышления младших подростков 11-12 лет. Им разработана методика обучения математике, построенная в форме квазиисследовательской деятельности. Она оказала существенное влияние на развитие теоретического мышления младших подростков и на успешность усвоения ими самого содержания математики. В таком обучении реализовываются познавательная активность подростков и поисковая направленность их сознания.

В образовательной практике России сложилась ситуация, когда большое число выпускников классов, обучающихся в начальной школе по системе развивающего обучения Д. Б. Эльконина — В. В. Давыдова, переходят в среднее звено общеобразовательных учебных заведений. Целью развивающего обучения является активизация основ теоретического мышления, его основных компонентов: анализа, планирования, рефлексии.
Каковы реальные возможности развития теоретического мышления младших подростков V — VI классов? На наш взгляд, возрастные возможности младших подростков при обучении математике используются недостаточно. Мы предполагаем, что обучение математике, построенное по содержанию и в форме квазиисследовательской деятельности, может существенно влиять на развитие теоретического мышления младших подростков и на успешность усвоения ими самого содержания математики. Организованные таким образом занятия позволяют продолжить содержание предшествующего обучения и развития в начальной школе, могут существенно влиять на индивидуальную траекторию интеллекта. Основания для такой гипотезы следующие.
Учащиеся присваивают культурные формы в процессе учебной деятельности, осуществляя при этом мыслительные действия, адекватные тем, посредством которых исторически вырабатывались продукты духовной культуры, т. е. школьники как бы воспроизводят реальный процесс создания людьми понятий, образов, ценностей и норм. Отсюда В. В. Давыдов делает важный вывод о том, что обучение в школе всем предметам необходимо строить так, чтобы оно в сжатой, сокращенной форме воспроизводило действительный исторический процесс рождения и развития знаний.
Ученику необходимо научиться исследовать условия задачи, отыскивать связи между свойствами объекта и возможными способами его преобразования. Этим условиям удовлетворяет поисково-исследовательская (квазиисследовательская, по определению В. В. Давыдова) деятельность [3].
Проект культурно-исторического типа школы (В. В. Рубцов, А. А. Марголис, В. А. Гуружапов), охватывающий образовательное пространство от дошкольника до выпускника, предлагает возможность не вообще продолжить учебную деятельность, а строить учение как собственную квазиисследовательскую деятельность, характерную для обучения подростков. Задача приспособления современного человека к многомерности своего бытия может быть решена через снятие в процессе обучения самих форм исторических типов сознания и деятельности, т. е. обобщенных (и исторически определенных) способов работы с миром вещей и миром идей. Третья ступень культурно-исторического типа школы для подростков 10 — 14 лет должна, по замыслу авторов, создавать условия, необходимым образом моделирующие формы, присущие такому типу деятельности, как исследование [4].
В традиционной системе обучения не ставится задача формирования способности к теоретическому осмыслению явлений действительности, и в ней нет содержания, на котором эту задачу можно было бы решать, не формируется и способность видеть в отвлеченных формулах реально происходящие процессы.
В практике развивающего обучения объективно существуют два типа квазиисследовательской деятельности.
Первый наблюдается при условии, что учебная деятельность воспроизводит способ изложения исследователями результатов своей деятельности. Этот тип поисковоисследовательской деятельности реально отражен в технологии обучения. Вместе с тем этот тип может быть назван дискуссионно-аналитическим.
Однако в практике развивающего образования у ученика часто возникают переживания сродни переживаниям исследователя, первооткрывателя, выступающие проявлением аналогов исследовательского подхода к изучаемому предмету. На фоне таких переживаний и учебная деятельность претерпевает существенные изменения. Это те самые ситуации, благодаря которым способ производства продуктов духовной культуры в сокращенном виде возникает в индивидуальном сознании школьника, когда он вдруг открывает и сам формулирует закономерности строения объекта, как бы спонтанно делает самостоятельные обобщения относительно изучаемого материала. В этом случае учебная ситуация будет складываться иначе, чем для ученика, не испытавшего таких переживаний. Такой тип действий назовем квазиисследовательской деятельностью второго типа. Первый тип развития более проработан в технологии развивающего образования, второй также имеет место в рамках системы Д. Б. Эльконина — В. В. Давыдова. Реально ситуации второго типа наблюдаются редко. Благодаря особому содержанию программ в учебном процессе закономерно возникают ситуации возможного духовного взлета учеников, хотя сам момент «открытия» для учителя и ученика, как правило, непредсказуем. В узловых, поворотных точках образовательных траекторий, в которых принципиально возможен скачок в развитии детей, следует быть готовым поддержать их в попытке выйти на более высокую образовательную траекторию.
В. А. Гуружапов высказал предположение, что второй тип исследовательской деятельности в начальной школе, возникающий случайно в силу самого содержания, в подростковом возрасте может специально культивироваться через совершенствование методики обучения, так как содержание предметов теоретических дисциплин само по себе предполагает широкие обобщения [1, 2].
Наиболее отчетливо способность учеников к такому типу деятельности проявляется при решении нестандартных задач, где при анализе условия и решении задачи фактически нужно проводить мини-исследование.
Для примера рассмотрим логико-предметный анализ одной из таких задач.

Задача

Нанизывание рябины на нить представляет собой равномерный процесс (при условии плотного расположения ягод и их одинакового размера).
Его характеристики: S — длина нити, занятой рябиной, T — количество использованных ягод (см. рисунок на с. 60).
Оборудование: нить, линейка, рябина, весы бытовые, весы лабораторные, небольшая чашка, стеклянная банка (мензурка), резинка.

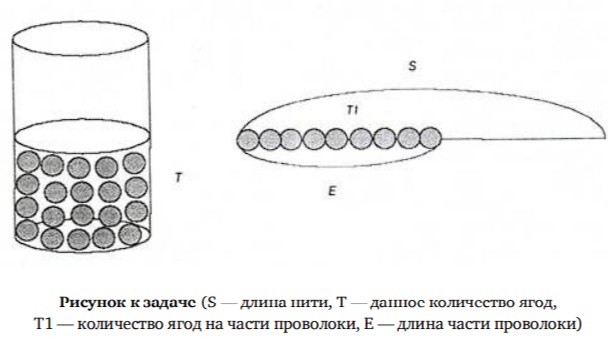
Рисунок к задаче (S — длина нити, T — данное количество ягод,
T1 — количество ягод на части проволоки, Е — длина части проволоки)
Сколько нужно ягод для заполнения нитки заданной длины (S)?
Какой длины нить может быть заполнена данным количеством ягод? (Ягоды насыпаны в мензурку.)
Предполагаемые способы решения задачи 2:
Можно непосредственно нанизывать ягоды, но это достаточно трудоемкое по времени занятие, хотя, в принципе, сделать это можно.
Выяснить, какая длина нити (Е) заполнится определенным количеством ягод (например, Т1 = 10 шт.). Пересчитать все ягоды (T). Найти T/T1=N. Найти искомую длину S= E N.
Зафиксировать некоторую длину нити (Е). Выяснить, сколько нужно ягод для ее заполнения (Т1). Пересчитать все ягоды (Т). Найти T/T1?=N. Найти искомую длину S= Е — N.
Взвесить все ягоды. Разбить их на N равных частей. Нанизать одну такую часть ягод на нить. Измерить полученную длину (Е). Найти искомую длину S=E • N.
При условии запрета на пользование весами отсыпать ягоды из стеклянной банки в маленькую чашку. Нанизать их на нитку и измерить длину занятой части (Е). Узнать, сколько таких чашек умещается в банке (N). Найти искомую длину S= Е • N.
Приведем описание реального решения задачи 2 учениками V класса гимназии V 10 г. Пушкино в начале учебного года. Задача была предложена после решения задачи 1 на предыдущем занятии.
Учитель. В мензурку насыпана рябина. (Верхний уровень рябины отмечен резинкой.) Имеется проволока. Задача, обратная той, которую мы решали в прошлый раз. Кто догадался, какую задачу мы будем решать сегодня?
Сергей. Сколько проволоки понадобится на данное количество рябины?
Учитель. Верно. Дана рябина. Какой длины проволоку нужно взять, чтобы нанизать на нее всю эту рябину?
Лиана. Мне кажется, на проволоку надо нанизать 10 ягод, потом отмерить, сколько это будет сантиметров.
Дети. А откуда ты знаешь, сколько там всего рябины?
Учитель. Можно ли дополнить способ Лианы?
Поля. Нужно подсчитать, сколько всего находится рябининок в мензурке, и умножить на количество рябининок длину 10 ягод.
Сергей. Нужно поделить сначала на 10.
Учитель. Давайте предположим, что в мензурке 200 ягод. Тогда на сколько нужно умножить длину 10 рябин?
Поля. На 20. Такое расстояние занимают 10 рябининок, а не одна, поэтому нужно сначала 200 разделить на 10, получится 20, а затем 20 умножить на длину, заполненную 10 ягодами.
Учитель. Чем неудобен такой способ?
Дети. Трудно подсчитать, сколько всего ягод в мензурке.
Учитель. Попробуйте придумать другой способ.
Глеб. Нужно взять проволоку и обмотать мензурку по рядам, там же рябина рядами лежит.
Л и а н а. А внутри, в серединке, там тоже есть рябина.
Саша. Получается, что мы учтем только ту рябину, которая лежит по бокам.
Сережа. Еще долгий способ есть. Нужно просто насаживать на проволоку всю рябину.
Учитель. Обратите внимание, какие предметы лежат на столе. Их можно использовать для решения задачи.
Глеб. Нужно из мензурки насыпать в маленькую чашку. Затем взвесить ягоды в мензурке. (Ставит на весы мензурку с ягодами. Получается 750 г.)
Дети. А сама мензурка тяжелая, она тоже вес дает.
Сергей. Я хочу предложить новую версию способа Глеба. Нужно подсчитать, сколько ягод вмещается в чашку, а потом посмотреть, приставить вот так. (Приставляет чашку к мензурке, узнавая, сколько раз она умещается по высоте.) Потом узнать, сколько ягод в чашке и сколько всего ягод в мензурке. А потом сделать по Лианиному способу.
Саша. Была бы чашка такой же толщины, тогда получилось бы.
Учитель. А можно точнее узнать, сколько во всей мензурке таких чашек?
Павел. Можно. Надо один раз взять, отсыпать куда-нибудь, другой раз взять, и сколько раз так мы возьмем, столько будет чашек. Потом число ягод в одной чашке умножить на количество чашек.
Учитель. А как проще узнать, сколько в мензурке чашек?
Ксения. В мензурке осталось место от того, что мы отсыпали рябину. Можно измерить это пространство линейкой. (Измеряет линейкой. Получается 3 см.)
Сергей. Теперь нужно измерить все расстояние, занятое рябиной, и поделить на 3. (Измеряет расстояние от дна до верхнего уровня рябины. Получает 19 см.)
Дети. Получается 6 с половиной чашек.
Сергей. Шесть и одна треть.
Учитель. Давайте округлим до 6 чашек. Итак, в мензурке осталось 6 чашек, и еще одну мы отсыпали. Всего в мензурке 1 чашек.
Дети. Теперь нужно подсчитать, сколько ягод в чашке, и умножить на 7.
Володя Ничего не понял.
Лиана. Мы отсыпали 1 чашку и стали мерить, сколько чашек в мензурке. У нас получилось 7 чашек.
Глеб. Теперь нужно подсчитать, сколько в 1 чашке ягод, и умножить на 7. Мы узнаем, сколько всего ягод в мензурке, а затем применим способ Лианы.
Дети. Давайте подсчитаем, сколько ягод в чашке. (Три девочки пересчитывают рябину из чашки. Получают 91 ягоду.)
Учитель. Будем считать, что в чашке 90 ягод.
Дети. Значит, всего в мензурке 630 ягод.
Учитель. Вспомним из прошлой задачи, какую длину занимают 10 ягод.
Дети. 9 см.
Учитель. Сколько займут 630 ягод?
Полина. 630 ягод надо разделить на 10, чтобы узнать, сколько раз по 9 см. Получается 63. 63 раза по 9 см дают 567 см, 5 м 67 см проволоки.
Учитель. Попробуйте придумать способ решения этой задачи, используя весы.
Саша. Надо узнать, сколько весит одна ягодка.
Учитель. Постарайся выбрать ягоду средних размеров. (Измеряем на весах
массу 1 ягоды. Получаем 500мг, полграмма.).
Саша. Теперь нужно измерить вес пустой мензурки. (Измеряет.)
Сережа. Проще измерить вес рябины в пакете. (Измеряет, получает 310 г.)
Юля. Теперь нужно 310 г умножить на полграмма.
Полина. Неправильно. Нужно 310 г разделить на полграмма.
Учитель. Вы пока не умеете делить 310 на 0,5.
Сережа. Нужно перевести 310 граммов в миллиграммы.
310 г=310 000 мг.
310 000: 500=620.
Всего 620 ягод.
Учитель. Можно было по-другому узнать, сколько всего ягод.
1 ягода —0,5 г, получается, что в 1 г — 2 ягоды, а всего 310 г, значит, всего
620 ягод.
Юля. Теперь нанижем 10 ягод на проволоку, получим 9 см.
Полина. 620: 10=62; 9 х 62= 558 (см).
Учитель. Как можно по-другому пересчитать ягоды?
Глеб. Можно все ягоды взвесить, взять оттуда 10 ягод и их взвесить. (Взве
шивает 10 ягод, получает 4 г 800 мг.)
Учитель. Чем больше мы берем ягод, тем точнее узнаем средний вес одной ягоды. Одна ягода весит 480 мг.
Сергей. Теперь нужно 310 000 разделить на 480. (Делит, получает приблизительно 645 ягод.)
Учитель. Мы получили более точный результат. Округлим его до 650 ягод.
Полина. 650: 10=65; 65 • 9=585 (см).
Учитель. Есть у вас желание придумать новый способ?
Дети. А у вас есть свой способ?
Учитель. Взвесим всю рябину. Получаем 310 г. Теперь берем гирьку, например, в 10 г и смотрим, сколько ягод уравновесят 10 г. В моем способе не надо использовать то, что 10 ягод занимают 9 см. Теперь рябину, которая весит 10 г, нанизываем на проволоку. При этом я не пересчитываю, сколько у меня ягод. Пока я нанизываю, сообразите: что нужно делать дальше?
Глеб. Теперь нужно измерить, сколько сантиметров заняла рябина. Получается 19 см. 10 ягод занимают 19 см. 310 г ягод займут 19 • 31 = 589 (см).
Можно выделить следующие особенности задачи:
в ее условии отсутствуют какие-либо числовые данные, что побуждает обучающихся самостоятельно устанавливать математические связи между объектами;
задача имеет не единственный способ решения, и дети могут предложить несколько разных подходов к ее решению;
задача не имеет одного правильного ответа, точнее, практически его трудно получить;
учитель при решении задачи является руководителем творческого семинара обучающихся.
Эти особенности отличают данную задачу от типичных учебных задач, решаемых посредством квазиисследовательской деятельности первого типа, когда взрослый, осуществляя определенную помощь и организуя взаимодействие детей, ведет их к заранее известному выводу. Вместе с тем в совокупности эмпирических данных, представленных в условии задачи, ученик открывает закономерности взаимных связей ее объектов, оказываясь в роли исследователя, что приводит его к квазиисследовательской деятельности второго типа. При этом дискуссионно-аналитический метод сохраняется как важный момент этой деятельности.
Задачи, подобные рассмотренной, решались детьми на факультативных занятиях в течение первого полугодия. Они вызывали неизменный интерес у обучающихся. В обсуждение вовлекалось большинство детей класса. Даже те ученики, которые не принимали видимого активного участия в обсуждении, следили за ходом решения задачи. Проведенное в начале учебного года обследование показало, что обучающиеся данного класса находятся на обычном уровне развития математического мышления. По нашему предположению, сама квазиисследовательская форма развития способствовала повышению интереса и активности детей. При предъявлении условия новой задачи ученики часто могли самостоятельно предугадать и сформулировать вопрос задачи. Особенно это было заметно при постановке новых задач, обратных решенным на предыдущих занятиях. Следует отметить, что во втором полугодии при решении обычных задач на сообразительность и смекалку и задач повышенной трудности, где требовалось применить математические знания в нестандартной ситуации, степень интереса к нашим занятиям заметно снизилась.
С точки зрения математического содержания обучения, решаемые нами задачи находятся в рамках традиционно изучаемого в школе материала. В рассмотренной задаче это прямая пропорциональная зависимость между величинами, решение пропорций, выход на действия с десятичными и обыкновенными дробями. По нашему мнению, нужно искать разумное соотношение между регулярным изучением курса математики и квазиисследовательской деятельностью второго типа, сохраняя при этом такой ее важный момент, как дискуссионно-аналитический метод.
Имеется еще одна потенциальная возможность использования рассмотренной задачи — анализ границ применимости полученного решения. Так, при решении первой задачи, когда рябина была свежесорванной, и при решении второй (обратной) задачи спустя неделю мы получили существенно различные результаты при проведении одних и тех же измерений. Очевидно, следовало задаться вопросом, почему это произошло, либо в конце решения задачи выяснить, не изменятся ли наши результаты через какое-то время. Но мы сами сразу не сообразили, что за неделю рябина просто усохла.
Подводя итоги обсуждения проблемы, изложенной в данной статье, мы приходим к выводу, что квазиисследовательская деятельность второго типа возможна как закономерная и специально организованная форма обучения подростков. В таком обучении могут реализоваться познавательная активность подростков и поисковая направленность их сознания.

1. Гуружапов В. А. Перспективы обучения школьников с повышенной мотивацией к учению в форме квазиисследовательской деятельности // Городская научно-практическая конференция «Столичное образование на рубеже XXI века». Вып. 2. М., 1999.
2. Гуружапов В. А. Развивающее обучение: чтобы урок был впрок // Управление школой. 1998. № 43.
3. Давыдов В. В. Теория развивающего обучения. М., 1996.
4. Рубцов В. В., Марголис А. А., Гуружапов В. А. Культурно-исторический тип школы: Проект разработки // Психологическая наука и образование. 1996. № 4.