В связи с увеличением потока иммигрантов из Мексики и ростом испаноговорящих детей в образовательных учреждениях Соединенных Штатов Америки встал вопрос, как построить образовательную программу, чтобы дети иммигрантов могли успешно обучаться английскому языку [Branum-Martin, 2006, с. 170-181], [Schatschneider, 1999, с. 439-449]. Поэтому американскими психологами была поставлена задача по исследованию фонематического восприятия у испаноговорящих детей. Целью работы было выявление степени общности восприятия фонем для различных языков, а также решение вопроса, в какой степени восприятие написанного слова отличается от восприятия фонемы слова. Исследование американских психологов было выполнено с помощью традиционного конфирматорного факторного анализа.
Разработанный альтернативный вариант конфирматорного факторного анализа позволяет находить параметры исследуемой модели прямым методом, позволяющим избежать трудоемкого и неоднозначного процесса итерационного решения задачи многомерной оптимизации [Neale, 1992] и обеспечивая однозначное оптимальное решение.
Традиционный конфирматорный факторный анализ предполагает наличие строго сформулированной модели изучаемого явления. Факторная модель, связывающая наблюдаемые и латентные переменные, составляется, опирается на знание предметной области. Гипотезы о структуре модели должны основываться на анализе природы исследуемых факторов (учитывается как теория, так и наблюдения) [Neale, 1992]. Можно делать количественные предположения о значениях корреляций между латентными переменными и величинах факторных нагрузок. Свободные параметры модели подбираются так, чтобы получить наилучшее, с точки зрения заданного критерия, приближение к матрицам корреляций (или ковариаций) между наблюдаемыми переменными.
Объектом конфирматорного факторного анализа являются ковариационные или корреляционные матрицы наблюдаемых переменных. Цель анализа - выявить значения параметров модели, которая с приемлемыми ошибками объясняет изменчивость наблюдений.
Конфирматорный факторный анализ имеет следующие особенности:
• ненулевые (свободные) факторные нагрузки в уравнениях модели и число исследуемых факторов определяются заранее;
• допускается корреляция между ошибками измерений;
• факторные нагрузки и ковариации между латентными переменными могут быть свободными параметрами модели или приравниваться заданным константам;
• допускается анализ нескольких групп моделей;
• можно проверять, согласуются ли заданные ограничения с результатами наблюдений;
• оценки свободных параметров определяются методом максимального правдоподобия.
С последней особенностью связана основная проблема метода. Для определения оценок свободных параметров модели методом максимального правдоподобия в качестве минимизируемого критерия используется функция:
F = [ln iSi - In ISI + tr(SS-1) - m] (N-1), где S - выборочная ковариационная матрица наблюдаемых переменных, £ - прогнозируемая ковариационная матрица наблюдаемых переменных, ISI и |S| - определители матриц S и S, tr(SZ-1) - след матрицы (SS-1), N - объем выборки, использованной для вычисления матрицы S, m - число наблюдаемых переменных [Лоули, 1967].
Элементы прогнозируемой ковариационной матрицы представляют собой аналитические выражения относительно свободных параметров модели [Bishop, 1975]. В случае многомерного нормального распределения наблюдаемых переменных значения критерия F описываются распределением хи- квадрат.
Таким образом, для определения свободных параметров модели необходимо численно решать итерационными методами достаточно трудоемкую задачу локальной многомерной оптимизации. Из этого в общем случае вытекает невозможность определения глобального минимума, так как в результате решения находится один из локальных минимумов, зависящий от начального приближения. Следовательно, решение неоднозначно.
Суть разработанного альтернативного варианта конфирматорного факторного анализа - составление переопределенной системы уравнений, решение которой осуществляется прямым методом, а также проверка адекватности полученных систем с помощью статистических критериев согласия [Куравский, 2007, с. 15-31], [Bishop, 1975], [Goldstein, 2003].
Для составления системы уравнений используется модель дисперсионных компонентов, которая предполагает равенство единице путевых коэффициентов регрессии. Каждой наблюдаемой дисперсии и ковариации ставится в соответствие уравнение, выражающее ее прогнозируемое значение через свободные параметры модели (дисперсии и ковариации латентных переменных) [Bollen, 1989], [Loehlin, 1987].
В результате составляется система уравнений
Ax = b,
где A - матрица системы, коэффициенты которой определяются, опираясь на факторную модель; b- вектор-столбец n выборочных оценок дисперсий и ковариаций, которые определяются по результатам наблюдений; x- вектор- столбец m искомых свободных параметров системы (компонентов дисперсий и ковариаций латентных переменных).
Рассмотрим вектор е = Ax[*] - b, представляющий невязку псевдорешения x переопределенной системы, полученного методом наименьших квадратов. Полагая в общем случае, что компоненты вектора невязок коррелированны, запишем их ковариационную матрицу в виде O2V. Сделав замены
b = V1/2 b0 A = V1/2 A0,
где V = V1/2 V1/2 , перейдем к системе
АоХ = Ьо , ковариационная матрица вектора невязок е0= V'1/2е которой имеет вид о2Е, где Е - единичная матрица.
Если система (3) невырождена (rank А = m), вектор невязки е0 имеет многомерное нормальное распределение, а
x* = (ATA0)-1ATb0 = (ATV-1A)-1 ATV-1b
псевдорешение системы (3), полученное методом наименьших квадратов, то это псевдорешение является оценкой максимального правдоподобия, а статистика
X2 = (b0 -A0x*)T(b0 -A0x.) / о2 = (b-Ax.)TV-1(b-Ax.) / о2
имеет распределение хи-квадрат со степенями свободы [Королюк, 1985].
При решении поставленной задачи использовались упрощенные путевые диаграммы и ряд допущений (диаграмма). В качестве наблюдаемых переменных выступают тесты на английском и испанском языках, с помощью которых исследовались школьники. Основная путевая диаграмма, взятая из результатов исследований американских психологов, была разделена на две независимые части: индивидуальный и групповой уровень. Значения дисперсий и ковариаций наблюдаемых переменных заменялись переменными: d1 23 4 для дисперсий и C1 2345 6 для ковариаций.
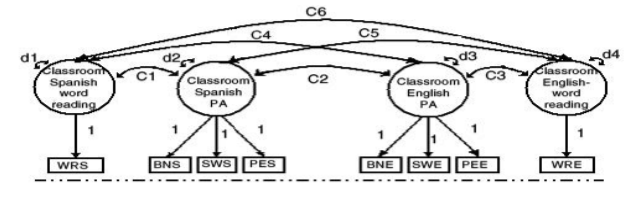
Предполагалось, что
- компоненты вектора невязок £ не коррелируют между собой;
- значения среднеквадратических отклонений различных компонентов вектора £ приравниваются к одному и тому же фиксированному проценту от соответствующих компонентов вектора b;
-указанный процент подбирается так, чтобы выполнялось равенство X2 >х2n-m; а при уровне значимости а = 0.05 (а- уровень значимости критерия), после чего эта величина оценивается на допустимость. (Уровень данной характеристики легче всего оценивать, установив для него разумное критическое значение, например, 0,1. Таким образом, вместо уровня значимости появляется новый критерий - критический процент.)
Разработанный альтернативный вариант конфирматорного факторного анализа позволяет также оценить статистическую значимость компонентов модели. Для этого необходимо провести сравнение двух моделей:
1) полной модели, в которой исследуемый компонент присутствует;
2) упрощенной модели, в которой этот компонент отсутствует.
Значение статистики хи-квадрат для упрощенной модели сравнивается с аналогичной характеристикой для полной модели. Поскольку разность указанных статистик асимптотически распределена как хи- квадрат с числом степеней свободы, равным разности в числах степеней свободы для полной и упрощенной моделей, эта разность используется для проверки нулевой гипотезы Hr о том, что упрощенная модель согласуется с результатами наблюдений, против альтернативной гипотезы Hf о согласовании с результатами наблюдений полной модели. Если гипотеза Hr не отвергается при заданном уровне значимости, то исследуемый компонент признается статистически незначимым и делается вывод о том, что имеющиеся данные не свидетельствуют о его влиянии на данную характеристику. Если гипотеза Hr отвергается (а гипотеза Hf принимается), можно говорить о влиянии исследуемого компонента на эту характеристику.
В исследованиях фонематического восприятия у американских школьников были выявлены взаимосвязи восприятия фонем на родном испанском языке и английском языке. Хорошее владение фонематическим восприятием на родном языке - испанском - обусловливает лучшее выполнение заданий на «чужом» английском языке, что наблюдалось как в результатах, полученных в индивидуальном тестировании учеников, так при тестировании всего класса. Таким образом, подтверждено влияние модели преподавания на развитие фонематического восприятия у испаноговорящих американских школьников [Branum-Martin, 2006, с.170-181].
Полученные оценки свободных параметров с помощью альтернативного факторного анализа не обнаружили значимых отличий от результатов, полученных с помощью традиционного конфирматорного факторного анализа, что позволяет подтвердить результаты американского исследования и говорит о перспективности нового подхода.