Введение нового образовательного стандарта ставит перед начальным общим образованием предельно важную задачу - научить детей учиться через формирование метапредметных образовательных результатов, основу которых составляют так называемые универсальные учебные действия. На наш взгляд, теория учебной деятельности и система развивающего обучения, разработанные выдающимися учеными Д.Б. Элькониным и В.В. Давыдовым [Давыдов В.В, 1986; Давыдов, 1996] и проверенные практикой, содержат в себе скрытые (неизвестные пока) возможности решения современных проблем отечественного образования, в том числе и проблем введения нового образовательного стандарта. Обнаружение таких возможностей является актуальной задачей теоретических и практикоориентированных исследований.
В нашей работе мы решаем эту задачу относительно учебного действия «принятие от учителя или самостоятельная постановка учебной задачи». Именно с самостоятельной постановки учебной задачи начинается формирование универсальных учебных действий, а значит и умения учиться. На основе анализа психологических и деятельностных механизмов этого учебного действия строится обобщенная модель постановки учебной задачи. Разработка методических материалов по этому вопросу будет полезна учителям при решении задач нового образовательного стандарта.
Наша работа направлена на поиск условий и требований к организации предметного содержания, обеспечивающих принятие и самостоятельную постановку детьми учебной задачи в условиях требований к предметным и метапредметным образовательным результатам нового стандарта.
Эта цель реализована в виде условий организации учебной деятельности для принятия и самостоятельной постановки учебной задачи, структуры изучаемого учебного действия, описания связей с другими обеспечивающими учебными действиями и методическими рекомендациями для учителя.
Объектом исследования выступили методы организации учебной деятельности по постановке и решению учебных задач, направленных на формирование метапредметных результатов.
Предметом исследования стали учебные действия принятия и самостоятельной постановки учебной задачи как способ постановки задач для формирования универсальных учебных действий.
Наша гипотеза состояла в следующем. Постановка учебной задачи для формирования универсальных учебных действий будет эффективной, если специальным образом сконструированная учительская задача удовлетворяет следующим требованиям:
 содержит «разрыв» (ситуацию невозможности решения задачи известными
содержит «разрыв» (ситуацию невозможности решения задачи известными
способами);
 организует рефлексивную остановку в деятельности детей по обнаружению дефицита средств;
организует рефлексивную остановку в деятельности детей по обнаружению дефицита средств;
 вынуждает детей искать новые средства для решения учительской задачи;
вынуждает детей искать новые средства для решения учительской задачи;
содержит этап понимания и оформления обнаруженного средства решения задачи как нового способа.
Задачи исследования формулировались следующим образом:
проанализировать учебное действие принятия и постановки учебной задачи,
его специфики и мотивационной основы в структуре учебной задачи;
 описать обобщенную операциональную структуру учебного действия, условия и требования к организации предметного содержания;
описать обобщенную операциональную структуру учебного действия, условия и требования к организации предметного содержания;
 разработать примеры и методические материалы, направленные на овладение учебным действием принятия и самостоятельной постановки учебной задачи;
разработать примеры и методические материалы, направленные на овладение учебным действием принятия и самостоятельной постановки учебной задачи;
 проверить эффективность разработанных методик для постановки учебной задачи для формирования универсальных учебных действий.
проверить эффективность разработанных методик для постановки учебной задачи для формирования универсальных учебных действий.
Учебное действие «принятие от учителя или самостоятельная постановка учебной задачи» занимает особое место в структуре учебной задачи [Давыдов, 1996, с. 159]. Оно даже появилось не сразу [Давыдов В.В, 1986, с. 154]. Это, на наш взгляд, связано с особым статусом категории «учебная задача» в теории развивающего обучения. Данное учебное действие вводит постановку задачи в систему ее решения, чем принципиально отличает учебную задачу от других задач. Тем самым задача формирования мотивационной основы решения задачи вводится в саму учебную задачу и задает линию формирования мотивов при переходе от одного учебного действия к другому. Именно связь постановки учебной задачи с ее решением и с мотивационной основой выполнения учебных действий делает это учебное действие актуальным для формирования универсальных учебных действий.
В основание анализа изучаемого учебного действия мы полагаем схему постановки и решения задач.

Рис. 1. Схема постановки и решения задач
Мы исходим из того, что в начальной школе для принятия задачи ребенку должны быть известны (понятны) два компонента из трех этой схемы (рис. 1). Как правило, это - условия (У) и средства (С), применение которых приводит к результату (Р).
Вот как это происходит на традиционном уроке. Учитель вводит детей в круг новых понятий, затем демонстрирует решение задач, где новые понятия выступают средством решения, а затем дает детям задачи для самостоятельного решения. Понимание условия задачи и знание средства решения обеспечивают принятие задачи, учебный мотив действия решения связан со средством, т. е. с тем образцом (способом) действия учителя, которым он демонстрировал свое решение. Этот образец позволяет ученику решить задачу, достигнуть цели.
В развивающем обучении каждый урок должен начинаться с ориентировки учеников в предстоящей деятельности, с актуализации и оценки уже освоенного ими способа решения. Это - необходимое основание для построения нового знания. В этом случае задачи, которые дает учитель, решаются по той же схеме (рис. 1), а в качестве средства могут выступать не только образцы действия учителя, но и способы, открытые самим учеником в предыдущей деятельности. Учебная мотивационная основа не меняется, она снова связана со средством решения задачи. А общая мотивация усиливается успешностью деятельности.
Следующий шаг - учитель дает детям задачу, содержащую «разрыв». Сначала детям кажется, что эта задача решается тем же только что продемонстрированным способом, поэтому в ситуации успеха они принимают задачу и начинают ее активно решать. Но постепенно дети обнаруживают, что известные им средства не достигают результата, и отказываются их применять для решения задачи. Происходит остановка в деятельности, казалось бы, исчезает учебный мотив. Но дети продолжают думать и что-то делать.
Как меняется учебная мотивация? Кажущая возможность решения задачи известным методом и желание решить задачу формируют образ результата [Давыдов В.В, 1986, с. 221], который вместе с опытом поисковой деятельности меняют ориентировочную основу действия до уровня шестого типа [Педагогическая психология /, 2013, с. 64]. Происходит «сдвиг» мотива на цель (на достижение результата в исходной задаче) [Леонтьев, 1959, с. 293-294], что вынуждает ребенка самостоятельно ставить задачу на поиск новых средств решения исходной задачи. Это «вынуждение» удерживает активность ребенка, открывает путь последующим учебным действиям и разным формам учебной деятельности.
В структуре постановки учебной задачи мы выделили две учительских задачи.
Назначение первой задачи состоит в следующем:
 актуализация средств, на содержании которых будет строиться новая учебная
актуализация средств, на содержании которых будет строиться новая учебная
задача, и проверка уровня овладения этими средствами учащимися;
 выход на «передний край» зоны ближайшего развития;
выход на «передний край» зоны ближайшего развития;
 создание ситуации успеха, соревновательности, мотивирования к учебной деятельности; задача как бы «замыкает» достижение образовательных результатов предыдущего шага, формирует уверенность педагога и учащихся в успехе предстоящей деятельности;
создание ситуации успеха, соревновательности, мотивирования к учебной деятельности; задача как бы «замыкает» достижение образовательных результатов предыдущего шага, формирует уверенность педагога и учащихся в успехе предстоящей деятельности;
 обозначение, фиксация с точки зрения «схемы интериоризации» индивидуального действия ребенка на применение освоенных знаний и способов;
обозначение, фиксация с точки зрения «схемы интериоризации» индивидуального действия ребенка на применение освоенных знаний и способов;
 создание позитивного отношения учителя, других учащихся, самого ребенка к его собственным, индивидуальным образовательным результатам.
создание позитивного отношения учителя, других учащихся, самого ребенка к его собственным, индивидуальным образовательным результатам.
Педагогическим и предметным содержанием первой задачи является завершение (подведение итогов) «чистового» выполнения учебного действия «решение частных задач» на освоенный способ действия, на освоенном предметном материале, как правило, на текстовых задачах.
«Чистовое» выполнение учебного действия - это значит ответственное (сделанное самостоятельно, на оценку) индивидуальное решение предложенной задачи на применение освоенных ранее знаний, умений и способов действия. «Чистовое» выполнение учебного действия «решение частных задач» всегда должно быть основано на самостоятельном принятии решения учеником задачи о его выполнении.
Вторая учительская задача - задача, содержащая «разрыв».
Ее назначение:
 создание максимального напряжения продуктивного учебного действия, невозможность отказа от деятельности;
создание максимального напряжения продуктивного учебного действия, невозможность отказа от деятельности;
 построение мотива учебного действия на постановку учебной задачи для открытия и создания нового средства, нового предметного содержания;
построение мотива учебного действия на постановку учебной задачи для открытия и создания нового средства, нового предметного содержания;
 диагностика и формирование зоны ближайшего развития.
диагностика и формирование зоны ближайшего развития.
Педагогическое и предметное содержание второй задачи: организация проблемной, неопределенной ситуации для поиска решения учениками (организация «тупика», «разрыва»); коммуникация с целью поиска средств моделирования условий задачи и до определения проблемной ситуации. Далее - новое предметное содержание, которое сначала выступает средством решения второй учительской задачи, а затем в коммуникации понимается и модельно оформляется как новое предметное знание.
Фактически, вторая учительская задача - начало нового предметного содержания. В основном оно организуется постановкой задачи по схеме постановки и решения задач.
Детям кажется, что известные им «старые» средства достаточны для решения этой задачи, - надо только постараться. И они с удовольствием включаются в процесс решения задачи (мотивация и «влипание» в деятельность). Важно фиксировать словесно и в моделях условие задачи и способы (средства) решения, которыми пользуются дети. Дети обнаруживают дефицит средств, результат сразу не достигается, действие останавливается, а продуктивный «запал» остается. Эта остановка является точкой поиска нового смысла, местом обнаружения и условием самостоятельной постановки учебной задачи. Вначале учебная задача здесь не ставится осознанно и рационально, она возникает как необходимость поиска новых средств. И только через коммуникацию и моделирование может быть оформлено условие самостоятельно оформленной задачи. Способность самостоятельно ставить задачу до ее решения формируется с развитием учебной деятельности.
Продемонстрируем выше сказанное на примере ряда задач. В соответствии с исследованием первой и второй частей данной работы мы покажем, какие изменения можно вносить в методику решения известных задач. Приведем пример собственной разработки, в которой покажем эффективность такого способа самостоятельной постановки учебной задачи. И приведем примеры задач, решение которых может продемонстрировать высокую степень сформированности метапредметных образовательных результатов.
Начнем с известной задачи «Домик», одной из первых задач по математике в I классе. Учитель вывешивает на доске домик и рядом с ним колонны на магнитах (рис. 2). Он говорит: «Вот домик и колонны (показывает домик, показывает колонны) после землетрясения одна колонна у домика разрушилась, что нужно сделать, чтобы крыша не упала?».
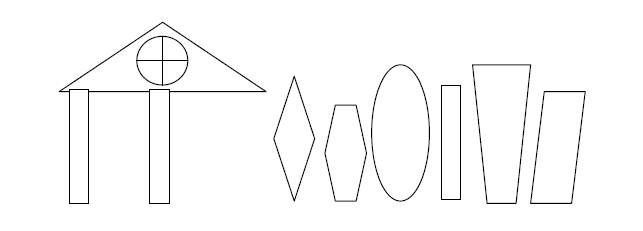
Рис. 2. Домик и колонны
По нашему представлению, эта задача должна состоять из трех последовательных вариантов.
Первый вариант - среди образцов колонн есть такая же по форме, как и остальные колонны домика. И в этом отношении для ученика, получившего «нормальное дошкольное образование», не составляет труда найти такую же колонну.
Второй вариант - среди образцов нет такой же колонны, но есть подходящая по длине (по высоте): она либо шире, либо уже. Ребенок должен отказаться от формы и поставить себе задачу, связанную с поиском нового средства, которое связано с понятием «такой же по длине», т. е. с равенством, - одним из основных отношений на величинах. Решение этой задачи откроет возможность дальнейшей коммуникации и понимания, что такое длина и что такое равенство длин.
Третий вариант - среди предложенных колонн нет ни одной подходящей по длине; такая задача не имеет решения. В этом варианте длина и равенство длин являются объектом понимания. Понятие «равенство длин» выступает как средство обоснования отсутствия решения.
Следующая задача называется «Третий способ уравнивания». Речь идет о предметном моделировании. На партах стоят по два сосуда с водой, с разными объемами. Детям предлагается их уравнять. После того, как они, переливая воду туда и обратно несколько раз, уравнивают объемы, учитель ставит следующую задачу: «Покажите на полосках то, что вы сделали?».
К этому времени дети уже умеют демонстрировать на полосках первый и второй способы уравнивания. Первый способ уравнивания связан с уменьшением большей величины до меньшей, второй - с увеличением меньшей величины до большей. Дети легко показывают уменьшение величины (объема, площади, массы и т. д.) путем отрезания от полоски ее части, а увеличение величины - приклеиванием к полоске недостающей части. Такая демонстрация фактически «копирует» предметное действие.
Суть этой задачи заключается в том, что третий способ уравнивания не «снимается», не «копируется» с предметного действия. Третий способ уравнивания должен быть найден теоретически, с помощью моделей. Такую задачу дети ставят и решают. Именно манипулирование с полосками и перенос полосок на классную доску для общей дискуссии (коммуникация и преобразование модели) позволит найти решение и сформулировать сам способ: отливать нужно половину разности объемов. Найденный способ позволяет по нему ставить задачу на построение предметного действия. Это одна из первых задач, где теоретическое решение лежит в основе предметного действия.
Приведем описание разработанных и спроектированных нами занятий на тему измерения площади прямоугольника.
Тема занятия: «Соотношение линейных мер и мер площади. Формула нахождения площади прямоугольника».
Ранее освоенный материал, лежащий в основании темы: измерение величины площади меркой, построение величины площади с помощью числа и мерки и моделирование (буквенное и графическое) при измерении и построение площадей.
Для эффективной постановки учебной задачи учеником в начале урока необходимо создать ситуацию успеха, актуализировать необходимые для изучения темы знания детей.
Задача 1. Учитель предложил ученикам прямоугольники из бумаги разных размеров и спросил: «Что общего у этих фигур?» Ученики ответили, что эти фигуры сделаны из бумаги, имеют четыре стороны, четыре угла, углы прямые, противоположные стороны равны. У них есть длина, ширина, площадь. Учитель поставил ученикам задачу измерить эти прямоугольники. Кто-то из детей попросил мерку. Учитель предлагает ученикам мерку в виде нитки. Дети отказываются ее брать и говорят о том, что площадь необходимо мерить меркой площади - квадратиком. Учитель дает мерку квадратик, и дети измеряют площади своих прямоугольников путем прикладывания квадратика. После измерения дети находят, что их прямоугольники имеют одинаковую площадь, хотя длина и ширина у них различна. Учитель просит зафиксировать полученный результат в виде формул и чертежей. После этого учитель отмечает успешную деятельность детей.
Задача 2. Учитель предлагает ученикам измерить площадь пола в классе, для этого он выдает кусок обоев размером 1м х 1м. Дети начинают измерять, двигать парты, но весь класс освободить не могут. Мебель в классе мешает им измерять. Но длину и ширину класса им удалось найти. И действие остановилось, дети говорят, что не могут померить. Единственный «наводящий вопрос», который может задать учитель, если все дети отказываются работать: «Но все-таки можно ли измерить площадь пола?» Важно выслушать все предложения детей, но особенно те, суть которых сводится к построению модели (чертежа измеряемой площади пола), и те, которые связаны с результатом измерения. Цель рисунка в данной ситуации - создать образ, модель действия. Суть этой задачи заключается в том, что ее можно решить с помощью модели. Возможный вариант рисунка на доске приведен ниже (рис. 3).
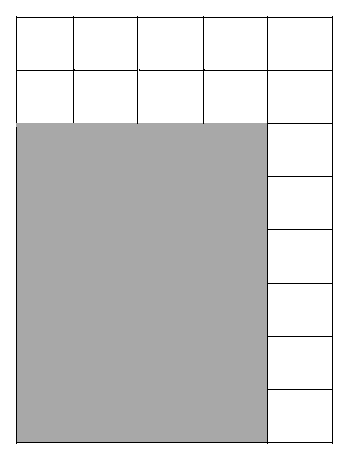
Рис.3. Модель нахождения площади пола
Преобразуя данную модель, дети могут заменить закрашенную часть клеточками и сосчитать результат измерения, зафиксировать его формулой и получить похвалу учителя.
Задача 3. Учитель показывает ребятам две веревки: одна длиной 3 м, вторая длинной 6 м и говорит, что это - длина и ширина прямоугольной площадки во дворе школы. Предлагает измерить площадку с помощью линейной мерки «е». Ученикам необходимо будет найти площадь прямоугольника и его построить. Мерка «е» равна 50 см. Условия построены таким образом, что стороны разные, но обе измеряются меркой «e» целое количество раз. «Разрыв» должен проявляться у детей не только в том, что прямоугольника нет, как в предыдущей задаче, но и в том, что нет самой мерки для измерения площади, ее надо построить. В этом построении - суть задачи. Дети «своими руками» создают суть связи линейных мер и мер площади.
Оформление этой связи и формулы площади прямоугольника происходит в следующих двух задачах.
Задача 4. При измерении строительной площадки квадратной меркой «е»,строители получили площадь, равную 24 е. Каковы длина и ширина этой площадки? Это неопределенная задача провоцирует поиск вариантов разложения произведения 24 на разные сомножители и поиск линейных мерок. В коммуникации по этому поводу окончательно оформляются и линейная мера сторон, и формула площади прямоугольника.
Задача 5.Учитель показывает ученикам две веревки разной длины, которые являются сторонами прямоугольника, и просит измерить площадь этого прямоугольника прямоугольной меркой со сторонами «е» и «f»,(«e» ^«f») . Наличие двух разных линейных мерок, которые по-разному измеряют параметры прямоугольника, проблематизирует формулу площади прямоугольника и дает возможность ученикам (теоретически) оформить суть формулы площади прямоугольника и связи линейных мер и мер площади как способа познания.
Следующую задачу мы предлагаем в качестве контрольной для самостоятельной работы.
Задача 6. Сравнить по площади два прямоугольника. Один - со сторонами 40 ярдов и 50 м, другой - со сторонами 50 ярдов и 40 м.
Таким образом, результатами нашего исследования являются: оформление обобщенного представления о способах организации учебной деятельности по самостоятельной постановке учебной задачи; логико-психологический анализ (структура мотивов) и способы организации предметного материала; собственные разработки по применению этих способов и оценки образовательных результатов.
База наших исследований - Красноярская прогимназия № 131. Здесь на учительских семинарах и занятиях с детьми проходили обсуждения и проверка наших исследований, и наши разработки о содержании и структуре учебного действия по постановке учебной задачи во многом являются обобщением того, что происходит в этой прогимназии и на уроках учителей, и на уроках студентов-стажеров. Достижения детей свидетельствуют об эффективности применения этих методов. Например, успешное участие наших детей на протяжении ряда лет в Международном дистанционном турнире по русскому языку и математике, победы в Краевых конкурсах по развивающему обучению.
Финансирование
Исследование выполнено при финансовой поддержке ГБОУ ВПО МГППУ в рамках Конкурса стипендии имени В.В. Давыдова.