Исследование уверенности в принятии решения

Анализируется процесс выполнения пороговых сенсорных задач. Дано краткое описание разработанной модели принятия решения и уверенности в его правильности. Экспериментальное исследование зрительного различения пространственных и временных признаков стимулов подтвердило предсказание модели о большей частоте правильных ответов среди уверенных по сравнению с частотой правильных среди всех ответов. Особенно это проявилось у рефлективных лиц.

Рассматривая проблему соотношения экспериментальных и не экспериментальных методов психологических исследований, следует отметить то важное место, которое в них занимает математическое моделирование. Моделирование – необходимый компонент системного метода изучения психического (Барабанщиков, 2005). Конечно, эксперимент имеет решающее значение для научного исследования. Однако он укоренен в специфику конкретной области науки. Модели же, как и вся математика, междисциплинарны по своей внутренней природе. Кроме того, на модели можно быстро провести проверку гипотезы, после чего она корректируется и окончательно проверяется в эксперименте. Воспроизведение экспериментально наблюдаемых психических феноменов в виде всесторонне проработанной математической модели позволяет одновременно описывать их структуру и механизмы, количественные взаимосвязи между их параметрами, формулировать и проверять гипотезы для экспериментального изучения. Моделирование интегрирует знания, накопленные в разных областях науки, и, объединяя их, служит «превращению технологии научно-исследовательской деятельности в технологию организации жизненной сферы человека… является важнейшим каналом реализации практического потенциала психологической науки. По этому же каналу осуществляется и обратное движение: регуляция методического обеспечения психологии, расширение и переоснащение ее технической, в том числе и аппаратурной базы» (там же, с. 27–28).

Рассматривая проблему соотношения экспериментальных и не экспериментальных методов психологических исследований, следует отметить то важное место, которое в них занимает математическое моделирование. Моделирование – необходимый компонент системного метода изучения психического (Барабанщиков, 2005). Конечно, эксперимент имеет решающее значение для научного исследования. Однако он укоренен в специфику конкретной области науки. Модели же, как и вся математика, междисциплинарны по своей внутренней природе. Кроме того, на модели можно быстро провести проверку гипотезы, после чего она корректируется и окончательно проверяется в эксперименте. Воспроизведение экспериментально наблюдаемых психических феноменов в виде всесторонне проработанной математической модели позволяет одновременно описывать их структуру и механизмы, количественные взаимосвязи между их параметрами, формулировать и проверять гипотезы для экспериментального изучения. Моделирование интегрирует знания, накопленные в разных областях науки, и, объединяя их, служит «превращению технологии научно-исследовательской деятельности в технологию организации жизненной сферы человека… является важнейшим каналом реализации практического потенциала психологической науки. По этому же каналу осуществляется и обратное движение: регуляция методического обеспечения психологии, расширение и переоснащение ее технической, в том числе и аппаратурной базы» (там же, с. 27–28).

Разработанная нами модель принятия решения (ПР) и уверенности (Ув), основанная на психофизической теории обнаружения сигнала (ПТОС), позволяет описывать вероятность правильности выбранного ответа и величину полезного результата не только в среднем по всей серии наблюдений, но и в каждом наблюдении (Шендяпин и др., 2008, 2010). Из выведенной в работе формулы для величины апостериорной вероятности присутствия в данном наблюдении сигнала P(sn|x)= 0,5 +0,5th{[C(x)]/2} следует, что правильность решения монотонно растет вместе с ростом введенной в парадигму ПТОС уверенности C(x). Величина Ув задается как натуральный логарифм произведения отношения априорных вероятностей стимулов на отношение правдоподобия (зависящее от величины сенсорного впечатления x в данном наблюдении) C(x)= ln [l0 l(x)] = L0+ L(x). Такое определение позволяет рассматривать Ув в выборе наиболее вероятного стимула как сумму двух свидетельств в пользу выбранного стимула: L0 = lnl0 = ln[P(sn)/P(n)] – несенсорного частотного, определяемого априорно заданными вероятностями стимулов, и L(x) = ln[l(x)] = ln[ f(x|sn)/f(x|n)] – сенсорного свидетельства, получаемого в процессе наблюдения. При C(x)>0 более вероятным является сигнал (ответ Y имеет вероятность правильности P(sn, Y|x) = 0,5 + 0,5th[C(x)]/2), при C(x)<0 более вероятным является шум (ответ N имеет вероятность правильности P(n, N|x)= 0,5 – 0,5th[C(x)]/2).

Установленная в экспериментах способность человека оценивать свою Ув в правильности сенсорного решения (см. обзор в работе Скотниковой, 2008) объясняется нами с помощью гипотезы о нормальности и равновариативности распределений сенсорных впечатлений человека в пороговой задаче. Известно, что в этом случае логарифм отношения правдоподобия упрощается до величины L(x)= d'(x – d'/2), определяемой только сенсорным впечатлением x и величиной d' – различимостью этих сенсорных распределений. Таким образом, для получения оценки Ув нейронам мозга человека не требуется реализовывать сложные вычисления – достаточно простых операций вычитания и умножения.

Разработанная модель объясняет механизм принятия решения рациональным наблюдателем в каждом наблюдении с помощью переживания Ув, которая выступает при этом еще и средством контроля правильности принимаемого решения. Модель также объясняет, как Ув используется для выбора ответа, обеспечивающего достижение максимальной величины полезного результата, определяемого априорно заданными ценами ответов vs , vs , v , v . К переменной, описыва n, Yn, Nn, Nn, Y ющей Ув в выборе наиболее вероятного стимула C(x)= L0+ L(x), добавляется третье несенсорное мотивационное свидетельство L= ln[(vs – vs )/(v – v )]. Таким Vn, Yn, Nn, Nn, Y образом, CV(x) – величина Ув в достижении максимального полезного результата равна сумме трех свидетельств CV(x)= L0+ L(x)+ LV. При CV(x)>0 лучше дать ответ Y, дающий средний полезный результат V(Y|x)=0,5(vs + v ) + 0,5(vs – v ) n, Yn, Yn, Yn, Y th[C(x)/2]. При CV(x)<0 лучшим является ответ N, дающий средний полезный результат V(N|x) = 0,5(vs + v ) + 0,5(vs – v )th[C(x)/2].

После получения сенсорного впечатления x и оценки величины CV(x) происходит ее сравнение с критерием ПР. При малых штрафах за ошибки добавочное мотивационное свидетельство LV лишь сдвигает критерий по оси ПР, но само правило ПР остается прежним. Если же испытуемый при больших штрафах за ошибки может отказываться от ПР в тех случаях, когда он не уверен в достижении заданной минимальной величины полезного результата, то правило ПР изменяется – на оси Ув появляется зона сомнений. Модель предсказывает, что при попадании CV(x) внутрь этой зоны вероятность вынесения ошибочного ответа столь велика, что ожидаемые значения полезных результатов V(Y|x) и V(N|x) становятся ниже допустимого минимума. Рациональный наблюдатель при этом должен отказываться от принятия решения, вынося ответ «сомневаюсь».

Чем шире зона сомнений на оси ПР, тем меньше остается уверенных ответов, но зато среди них больше верных, т. е. среди уверенных ответов частота правильных больше, чем во всем массиве полученных ответов. Разрешая наблюдателю отказываться от принятия решений, можно повысить их правильность. Для того чтобы описать это не только качественно, но и количественно, были проведены численные расчеты для задачи «больше–меньше» при величине различимости d' = 1,4. Зависимости вероятностей уверенных ответов P(Conf), правильных уверенных ответов P(Cor, Conf) и доли правильных уверенных ответов среди всех уверенных ответов P(Cor, Conf)/P(Conf) от ширины зоны сомнений, измеряемой в единицах среднеквадратичного отклонения, приведены на рисунке 1.

 

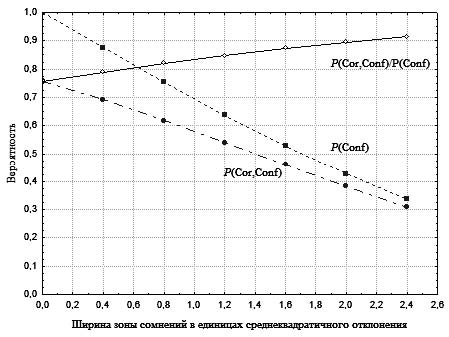
Рис. 1. Задача «больше–меньше», величина различимости d' = 1,4. Графики зависимостей вероятности вынесения правильных ответов P(Cor), вероятности вынесения правильных уверенных ответов P(Cor, Conf) и доли правильных ответов среди уверенных ответов P(Cor, Conf)/P(Conf) от ширины зоны сомнений, измеряемой в единицах среднеквадратичного отклонения

Этот теоретический результат был проверен экспериментально. Испытуемые различали сенсорные признаки объектов: пространственные при одновременном предъявлении стимулов и временные при последовательном их предъявлении. Использованы задачи различения двух основных видов: с ответами «больше–меньше» и с ответами «одинаковые–разные». Проверялось ключевое представление об Ув как факторе, монотонно связанном с правильностью решения.

А. Изучалась способность наблюдателя управлять правильностью решения сенсорной задачи с помощью Ув в принятом решении. В психофизическом эксперименте по методу констант 2 значения диаметра переменной окружности: большее и меньшее, чем эталон, подбирались околопороговыми для каждого наблюдателя, что дало 54–80 % правильных ответов, и предъявлялись в парах с эталоном равновероятно, в случайном порядке. Длительность предъявления составляла 600 мс, интервал между пробами – 1000 мс. Участвовали 47 испытуемых, с каждым из которых было проведено от 1 до 7 экспериментов, включавших по 2 серии, состоявших из 100–400 проб: каждая 1-я с ответами «больше–меньше», 2-я с ответами «больше–меньше–сомневаюсь». В целом был проведен 91 эксперимент (46613 наблюдений). Вычислялись: частота правильных ответов w1 в 1-й серии, частота правильных среди уверенных ответов wво 2-й серии и их разность Δw = w– w 2 21. Для контроля ошибок, возможных при замене теоретических вероятностей правильности на эмпирические частоты, в каждом эксперименте вычислялась σΔ – оценка среднеквадратичного отклонения случайной разности Δw. Полученные результаты приведены на рисунках 2, 3.

В подавляющем большинстве экспериментов (87 % случаев) частота правильных ответов среди уверенных была выше частоты правильных среди всех полученных ответов. Статистическая проверка значимости прибавки по всему массиву экспериментов, проведенная по критерию знаков, подтвердила неслучайный характер обнаруженной прибавки (p<0,01).

Б. В задаче «одинаковые–разные» испытуемые различали длительности световых вспышек. Длительность одного сигнала составляла 600 мс, длительность другого подбиралась околопороговой для каждого испытуемого, что дало 61–87 % правильных ответов. В каждой пробе испытуемые давали 2 ответа: «одинаковые» или «разные» длительности в паре и уверены или сомневаются они в правильности первого ответа. В 55 экспериментах, включавших по 100 проб каждый, участвовали 39 испытуемых. Как принято в психофизике (Индлин, 1976; Ferrel, 1995; Link, 2003), наша теоретическая разработка в целях наибольшей объективности проверялась по данным, полученным не только ее авторами, но и другими исследователями. Проанализированы данные 43 экспериментов Е.В. Головиной (2009) с участием 32 испытуемых, проведенных по этой же методике. По данным каждого испытуемого, во всех 98 экспериментах (9800 измерений) аналогично задаче «больше–меньше» вычислялись: частота всех правильных ответов w1; частота правильных среди уверенных ответов w2 и их разность Δw = w2– w1; оценка соответствующего среднеквадратичного отклонения σΔ. 

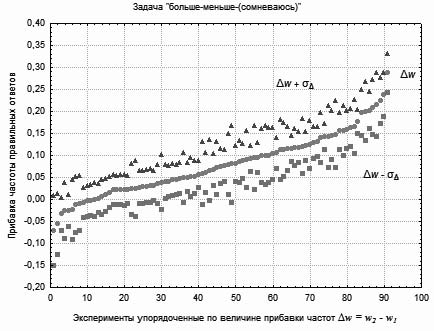
Рис. 2. Результаты выполнения задачи «больше–меньше)»: Δw – упорядоченная в порядке возрастания последовательность прибавок Δw индивидуальных частот w2 правильных ответов, полученных при выборе из 3-х категорий: «больше–меньше–сомневаюсь», относительно частот w1 правильных ответов, полученных при выборе из 2-х категорий: «больше–меньше». Последовательности точек Δw – σΔ и Δw + σΔ показывают диапазон вариативности полученных значений прибавок Δw ± σΔ

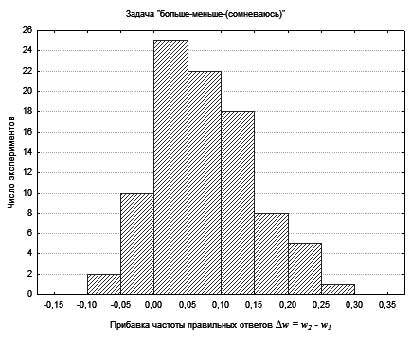
Рис. 3. Гистограмма распределения прибавок Δw индивидуальных частот w2 правильных ответов при выборе из 3-х категорий: «больше–меньше–сомневаюсь» относительно частот w1 правильных ответов при выборе из 2-х категорий: «больше–меньше»

Вновь в большинстве экспериментов (в 85 % случаев) частота правильных ответов среди уверенных была выше, чем частота правильных среди всех получен ных ответов. Графики индивидуальных данных аналогичны полученным в задаче «больше–меньше» (рисунки 2, 3). При этом прибавка частоты правильных ответов, оцененная по всему массиву экспериментов, также является неслучайной (p<0,01).

Сравнение данных в обеих задачах показало, что инструкция, прямо стимулирующая испытуемых стремиться к максимальной правильности уверенного решения, т. е. осознанно управлять правильностью решения (в задаче «больше–меньше»), позволила получить в среднем вдвое большую прибавку частоты правильных ответов среди уверенных относительно частоты всех правильных ответов, чем инструкция, в которой Ув не связывалась напрямую с ростом правильности (в задаче «одинаковые–разные»). Статистическая проверка достоверности различия прибавок частот правильных ответов, выполненная по критерию Манна–Уитни, показала, что сдвиги, полученные в задаче «больше–меньше», значимо выше сдвигов, полученных в задаче «одинаковые–разные» (p<0,00003).

Итак, правильность уверенных ответов превышала правильность всех полученных ответов в обоих основных видах задач различения: «больше–меньше» и «одинаковые–разные» для пространственных признаков зрительных объектов, предъявлявшихся одновременно, и для временных признаков, предъявлявшихся последовательно, соответственно. Т.е. установленный факт имеет достаточно общее значение.

Способность повышать частоту правильных ответов с помощью уверенности – сомнений сильно варьировала среди участников эксперимента. Для выяснения, не связана ли эта способность со свойствами индивидуальности, было проведено диагностическое исследование. Дифференциально-психофизические исследования выполняются с участием не сотен испытуемых (в отличие от дифференциально-психологических, когда с каждым проводится 1–2 измерения по конкретной методике), а лишь десятков и даже менее десяти, что достаточно для получения значимых результатов в силу большого объема (десятков и сотен) сенсорных измерений (Войтенко, 1991; Кочетков, Скотникова, 1993).

У 11 испытуемых из 47, выполнявших задачу «больше–меньше», определялись характеристики когнитивных стилей «рефлективность–импульсивность» по тесту Кагана и опроснику Азарова, «ригидность–флексибильность» по тесту Струпа и опросникам Айзенка, Белоуса и Бренгельмана, а также склонность к риску по опроснику Когана, Валлаха.

Ранговый корреляционный анализ трех видов (Спирмена, «гамма» и «тау Кендалла») выявил значимо отрицательную взаимосвязь между увеличением частоты правильного различения стимулов при использовании уверенных ответов и числом ошибок в тесте Кагана. Факторный анализ для 1, 2 и 3 факторов показал, что увеличение точности решения сенсорной задачи вошло только в 1-ый наиболее значимый фактор вместе с показателями теста Кагана (числом ошибок и временем 1-го ответа) и индексом Азарова. Т.е. 1-й фактор можно назвать «импульсивностью–рефлективностью». Рефлективные более осознанно управляют правильностью решения сенсорной задачи с помощью Ув, чем импульсивные. Это можно объяснить тем, что у импульсивных более низкий (либеральный) критерий ответа об Ув (более близкий к критерию основного ответа о различии стимулов), которым они плохо управляют в силу недостаточной сформированности механизмов наблюдения за своим поведением, его контроля и регуляции. Такая интерпретация объясняет данные Скотниковой (2008) и Головиной (2009) о большей Ув импульсивных лиц в своих сенсорных суждениях, по сравнению с рефлективными. Повышенная Ув импульсивных может быть следствием более низких порогов принятия уверенных решений, чем у рефлективных.

Разработанная модель развивает психофизическое описание механизмов принятия решения и уверенности и объясняет ряд проявлений этих феноменов в эксперименте.

1. Барабанщиков В.А. Принцип системности в современной психологии: основания, проблемы, тенденции развития // Идея системности в психологии. М.: Изд-во ИП РАН, 2005. С. 9–47.
2. Войтенко Т. П. Когнитивные стили и особенности сенсорной деятельности // Проблемы дифференциальной психофизики. М.: Изд-во ИП АН СССР, 1991. С. 93–110.
3. Головина Е. В. Уверенность и адекватность ее оценки при решении сенсорной задачи: когнитивно-стилевой аспект // Современная психофизика. М.: Изд-во ИП РАН, 2009. Гл. 22. С. 461–473.
4. Индлин Ю. А. Модель обучаемого наблюдателя в ситуации обнаружения и различения // Проблемы принятия решения. М.: Наука, 1976. С. 56–77.
5. Кочетков В. В., Скотникова И. Г. Индивидуально-психологические проблемы принятия решения. М.: Наука, 1993.
6. Скотникова И. Г. Проблемы субъектной психофизики. М.: Изд-во ИП РАН, 2008.
7. Шендяпин В. М., Скотникова И. Г., Барабанщиков В. А., Тарасов В. Б. Математическое моделирование уверенности при принятии решения в сенсорных задачах // Психологический журнал. 2008. № 4. С. 84–97.
8. Шендяпин В. М., Барабанщиков В. А., Скотникова И. Г. Уверенность в решении: моделирование и экспериментальная проверка // Экспериментальная психология. 2010. Т. 3. № 1. С. 30–57.
9. Ferrel W. R. A model for realism of confidence judgments: implications of underconfidence in sensory discrimination // Perception & Psychophysics. 1995. V. 57. P. 246–254.
10. Link S. W. C. S. Pierce, confidence and random walk theory // Fechner Day’2003: Proc. 13th Ann. Meet. Intern. Soc. for Psychophysics. Stockholm, 2003.