Измеряемые психологами параметры, как правило, не представляют исследуемые характеристики в форме, удобной для непосредственной интерпретации и определения надежных критериев, необходимых для психологической диагностики. Поэтому в случае многомерных измерений исследователи стараются выявить несколько латентных факторов, отвечающих за изменчивость наблюдаемых параметров, и, определив их природу, использовать далее полученную информацию для анализа собранных данных.
При этом обеспечивая минимальные потери полезной информации, параметры, которые легко измерить, по возможности, исследователи заменяют на такие, которые легко интерпретировать. При последующем анализе определяются функциональные зависимости наблюдаемых параметров от выявляемых факторов. В итоге выявляется вся структура причинных связей между факторами и наблюдаемыми переменными, а также если потребуется, непосредственные значения факторов, необходимые для идентификации состояния испытуемых.
Для выявления статистических связей между влияющими факторами разработан метод конфирматорного факторного анализа [Neale, 1992]. Однако практическое применение этого подхода обусловлено рядом серьезных ограничений, которые зачастую делают его использование невозможным. В частности, для анализа необходимо решение трудоемкой задачи многомерной локальной оптимизации, обеспечивающей оценку величин свободных параметров модели, что, как правило, не позволяет найти глобальный минимум и приводит к неоднозначности решения. Кроме того, этот метод обычно требует определенных вероятностных распределений результатов наблюдений, степень согласованности с которыми сложно проверить на практике из-за ограниченности выборки исследуемых данных [Куравский, 2003].
Преодоление указанных проблем обосновывает актуальность разработки нового подхода и отработки его практического применения на ряде профильных прикладных задач. В связи с этим в данной статье представлен комплекс новых методов решения рассмотренной задачи, опирающийся на возможности самоорганизующихся карт Кохонена и метода Монте-Карло [Ермаков, 2009].
Оценка степени адекватности факторных моделей
Конфирматорный факторный анализ предполагает наличие строго определенной факторной модели изучаемого явления, которая связывает латентные и наблюдаемые переменные и формируется, опираясь на знание предметной области. Гипотезы о структуре модели должны основываться на анализе природы исследуемых факторов. Можно делать количественные предположения о значениях факторных нагрузок и корреляциях между факторами, а также проверять гипотезы о структуре и свойствах моделей, подбирая их оптимальные варианты. Параметры моделей подбираются так, чтобы обеспечить наилучшее с точки зрения заданного критерия приближение к ковариационным (корреляционным) матрицам наблюдаемых переменных.
Объектами данного вида анализа являются ковариационные или корреляционные матрицы наблюдаемых переменных. Цель анализа - выявить значения параметров модели, которая с приемлемыми ошибками объясняет изменчивость наблюдений.
При использовании этого подхода:
• ненулевые (свободные) факторные нагрузки и число исследуемых факторов в модели определяются заранее;
• допускаются корреляции между ошибками измерений;
• факторные нагрузки и ковариации между латентными переменными могут быть свободными параметрами модели или приравниваться заданным константам;
• допускается анализ нескольких групп моделей;
• можно проверять, насколько согласуются ограничения, налагаемые на параметры модели, с результатами наблюдений.
Для определения оценок свободных параметров модели методом максимального правдоподобия в качестве минимизируемого критерия используется функция
![]()
где S - выборочная ковариационная матрица наблюдаемых переменных, Σ - прогнозируемая ковариационная матрица наблюдаемых переменных, |Σ| и |S| - определители матриц Σ и S, tr(SΣ-1) - след матрицы (SΣ-1), N - объем выборки, использованной для вычисления матрицы S, q - число наблюдаемых переменных [Куравский, 2009].
Элементы прогнозируемой ковариационной матрицы представляют собой аналитические выражения относительно свободных параметров модели. В случае многомерного нормального распределения наблюдаемых переменных значения критерия F описываются распределением c2.
Однако корректное использование метода максимального правдоподобия для идентификации значений свободных параметров и оценки степени адекватности модели, описанное выше для традиционного варианта конфирматорного факторного анализа, предполагает проверку многомерной нормальности наблюдаемых переменных. Эта процедура является трудоемкой и зачастую невозможной из-за малой выборки исследуемых данных [Мармалюк, 2010]. Кроме того, при традиционном конфирматорном факторном анализе критерий максимального правдоподобия является очень чувствительным к объему выборки: сравнительно небольшие отклонения от прогнозируемых характеристик приводят к существенному ухудшению согласования модели с наблюдениями. Использование данного метода невозможно также из-за нелинейности исследуемых моделей.
Для преодоления указанных проблем предлагается новый метод исследования адекватности факторных моделей интеллекта [Kuravsky, 2011], в соответствии с которым следует:
- выразить аналитически наблюдаемые дисперсии и ковариации через свободные параметры используемой факторной модели, составив переопределенную систему алгебраических уравнений, которая в общем случае является нелинейной;
- вычислить псевдорешение полученной системы уравнений с помощью подходящего численного метода.
Указанная переопределенная система уравнений может быть представлена в следующем виде.
F(x)=b,
где F(x) - n-мерный нелинейный оператор, действующий на m-мерный вектор x свободных параметров модели, компоненты которого являются аналитическими выражениями прогнозируемых дисперсий и ковариаций наблюдаемых переменных через m свободных параметров рассматриваемой факторной модели; b - вектор-столбец, составленный из n выборочных оценок дисперсий и ковариаций наблюдаемых переменных.
Для вычисления данного псевдорешения может применяться любой подходящий численный метод нелинейной многомерной локальной оптимизации, в котором критерий минимизации представлен евклидовой нормой невязки. В частности, для этого приемлемы градиентные методы. В процессе решения определялись оптимальные параметры модели - вектор псевдорешения. Дальнейшая оценка степени адекватности факторных моделей интеллекта проводится путем анализа полученного вектора псевдорешения.
Оценка степени адекватности нелинейных моделей путевых коэффициентов наблюдениям основывается на сравнении вектора невязки e псевдорешения и случайной выборки векторов невязок er для его окрестности, в которых определенный процент случайных компонентов выходит за границы доверительных интервалов. Векторы невязок er вычисляются с использованием рассматриваемой факторной модели.
Полученные выборочные оценки дисперсий и ковариаций наблюдаемых параметров позволяют вычислить вектор псевдорешения с помощью метода наименьших квадратов, а затем оценить вектор невязки псевдорешения по следующей формуле:
ε=F(x* )–b.
Данная оценка показывает, насколько рассчитанное псевдорешение x* согласуется с наблюдаемыми параметрами.
С целью получения информации о наиболее правдоподобных отклонениях идентифицируемых параметров от их оценок, полученных с помощью заданной факторной модели, для обучения самоорганизующихся карт признаков генерируются серии выборок xr с различными стандартными отклонениями и средними процентами случайных компонентов, выходящих за границы доверительных интервалов. Векторы xr могут быть распределены произвольным образом, однако на практике удобно генерировать их нормально распределенными, варьируя соответствующее стандартное отклонение и число компонентов, выходящих за границы доверительных интервалов. Генерация выборок позволяет рассматривать представленный подход как одну из форм метода Монте-Карло [Ермаков, 2009]. Оценка векторов невязок для выборок сгенерированных значений выполняется по формуле:
εr=F(x.)-F(xr).
Выборка случайных векторов невязок sr используется для обучения самоорганизующихся карт признаков подходящей размерности с целью получения выборок евклидовых расстояний между векторами невязок, используемыми в качестве входных данных, и центрами нейронов-победителей обучен
ной сети. Учитывая достаточно высокую размерность векторов невязок, характерную для практических задач, можно говорить о том, что распределение полученных евклидовых расстояний близко к нормальному. Выборочные оценки средних и дисперсий этих расстояний идентифицируют указанное распределение и позволяют оценивать вероятности превышения расстояния между полученным вектором невязки псевдорешения и соответствующим центром нейрона-победителя, что дает возможность судить о степени адекватности модели наблюдениям. Схема вычисления предлагаемых оценок представлена на рис. 1. Процедура вычисления наборов векторов невязок реализована для каждой из исследуемых моделей отдельно (в связи с уникальностью системы прогнозируемых аналитических выражений для дисперсий и ковариаций) в среде графического программирования LabVIEW. Работа самоорганизующихся карт признаков моделировалась с помощью пакета STATISTICA Neural Networks.

Рис. 1. Процедура оценки степени адекватности факторной модели наблюдениям с помощью самоорганизующихся карт признаков и метода Монте-Карло
Для удобства дальнейшего анализа стандартные отклонения генерируемых выборок поддерживаются в отношении всех параметров равными заданному постоянному проценту от соответствующих средних значений. Сопоставление рассмотренных выше вероятностных мер адекватности моделей для различных стандартных отклонений и средних процентов компонентов, выходящих за границы доверительных интервалов, позволяет выявлять наиболее правдоподобные сочетания достигнутой точности идентификации, представляемой оценкой стандартного отклонения, и структуры значимых погрешностей в определении компонентов полученного псевдорешения. Геометрическая иллюстрация, поясняющая суть процедуры для нелинейного оператора F(x), приведена на рис. 2.
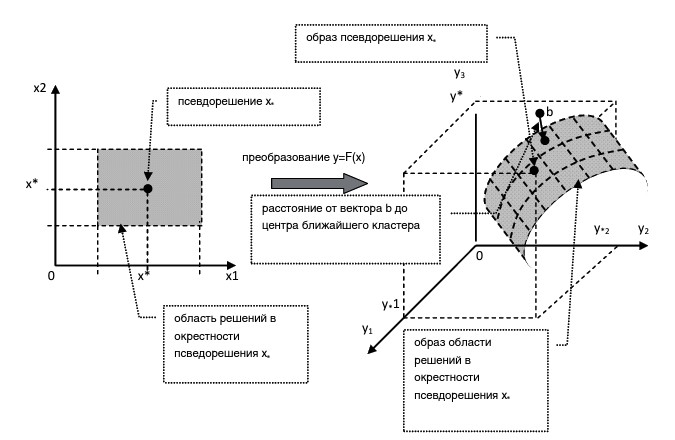
Рис. 2. Геометрическая интерпретация нелинейного преобразования области
В приведенной выше процедуре самоорганизующиеся карты Кохонена обеспечивают кластеризацию векторов невязок, которые связывают точку, заданную радиус-вектором F(x*), и точки, заданные радиус-векторами F(xr), с центрами радиальных базисных элементов, представляющих вычисленные центры кластеров. Размеры соответствующей топологической карты расширяются до тех пор, пока для генерируемой выборки векторов xr или не перестанут уменьшаться наибольшие частоты выигрышей на элементах, или не перестанет возрастать число нейронов-победителей. В этом случае, с точки зрения карты Кохонена, расстояния между векторами невязок sr и ближайшими к ним центрами кластеров уже не представляют геометрическое расположение точек, заданных радиус- векторами F(xr). Поэтому значения этих расстояний полагаются находящимися ниже «порога чувствительности» карт Кохонена и, следовательно, выражающими допустимые незначимые вариации («шум») расстояний от невязок до ближайших центров кластеров, которые не обусловлены геометрическим расположением [Галушкин, 2010].
Предлагаемый подход позволяет исследовать значимость различий между наиболее правдоподобными вариантами факторных моделей, используя технику проверки статистических гипотез, и опирается на возможности самоорганизующихся карт Кохонена и метода Монте-Карло. Свободные параметры этих моделей предварительно идентифицируются с помощью рассмотренного выше метода.
Оценка значимости различий между исследуемыми моделями
Сравнение опирается на сопоставление отношений r=o/m, где о - наиболее правдоподобное стандартное отклонение сгенерированных нормально распределенных значений свободного параметра модели, а m - соответствующее среднее значение распределения. Отношение r при генерации выборок поддерживается равным для всех параметров одной модели, но может различаться для разных моделей, которые, в общем случае, могут иметь и разные средние процентные соотношения компонентов, лежащих вне доверительных интервалов.
Пусть указанные отношения для сравниваемых моделей равны, соответственно, r1=s/m1 и r2=s2/m2, причем r1<r2. Сравнение моделей выполняется при одном и том же относительном стандартном отклонении s=r1=r2m2, когда среднее значение m1 выбирается в качестве единицы измерения (приравнивается к 1) и опирается на оценку вероятности получения приведенного среднего m2=r/r2, а именно: для случайной величины X вычисляется вероятность pm¿X<1)=tf1)-$(mJI пребывания в интервале [m2; m1=1], где Ф - функция нормального распределения со средним значением 1 и стандартным отклонением о,. Если эта вероятность превышает заданный критический уровень, который обычно принимается равным 0,05, различие между моделями рассматривается как статистически значимое, в противном случае - как незначимое.
Рассматриваемый подход позволяет определять объемы выборок, необходимых для проверки гипотез, что расстояние между векторами невязки псевдорешения g и соответствующими центрами нейронов-победителей обученной сети равно определенному значению для заданных уровней значимости и мощности выборки. Расчетная формула выводится из сравнения соответствующих областей принятия гипотезы:
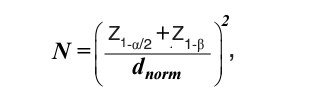
где Z1-а/2 и Z1-β квантили стандартного нормального распределения порядков 1-а/2 и 1-β, соответственно; а - уровень значимости; β - вероятность ошибки второго рода; dnorm - отношение отклонения истинного математического ожидания исследуемого расстояния от значения, постулируемого гипотезой, к стандартному отклонению распределения данного расстояния [Куравский, 2009а].
Преимуществами представленного метода являются:
- применимость для произвольных факторных моделей без взаимных влияний между переменными, образующих контуры обратной связи;
- отсутствие ограничений, налагаемых на распределения наблюдаемых переменных и компонентов вектора невязки (для которых ранее требовалось проверять соответствие многомерному нормальному распределению);
- наличие простой процедуры оценки вероятностей появления статистических ошибок 2-го рода;
- возможность выявления наиболее правдоподобных сочетаний достигнутой точности идентификации и структуры значимых погрешностей в определении компонентов полученного псевдорешения;
- возможность получения оценок адекватности моделей с заданной степенью точности путем соответствующего увеличения объема генерируемых случайных выборок компонентов псевдорешения.
Результаты практического применения представленного подхода
Согласно ведущим теориям, описывающим структуру интеллектуальных способностей, были разработаны различные варианты факторных моделей интеллекта применительно к результатам исследования соответствующих способностей монозиготных и ди- зиготных близнецов (рис. 3-5) [Куравский, 2011].
Иерархическая и гнездовая модели были составлены согласно подходам Ч. Спирмена и Л. Терстоуна к структуре интеллектуальных способностей [Ушаков, 2003]. Аддитивная и мультипликативная модели были разработаны с целью нахождения наиболее полной, согласующейся с наблюдениями модели интеллекта. Согласно каждой из моделей составлена матрица прогнозируемых оценок дисперсий и ковариаций, которая является объектом дальнейшего анализа.
На рис. 3 представлена иерархическая модель интеллекта, особенностью которой является то, что фактор G (генеральный фактор) непосредственно влияет на факторы вербального V и невербального N интеллекта.

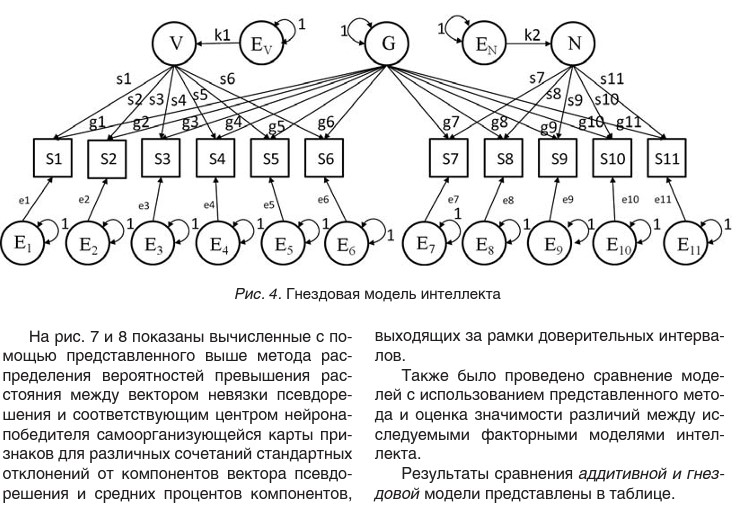
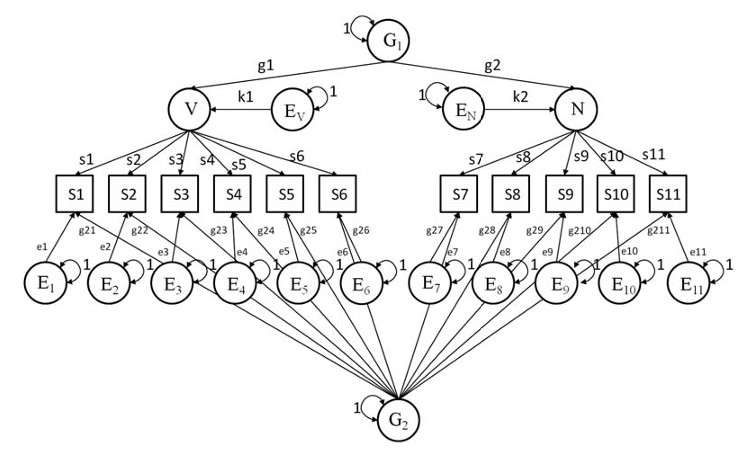
Рис. 5. Аддитивная модель интеллекта
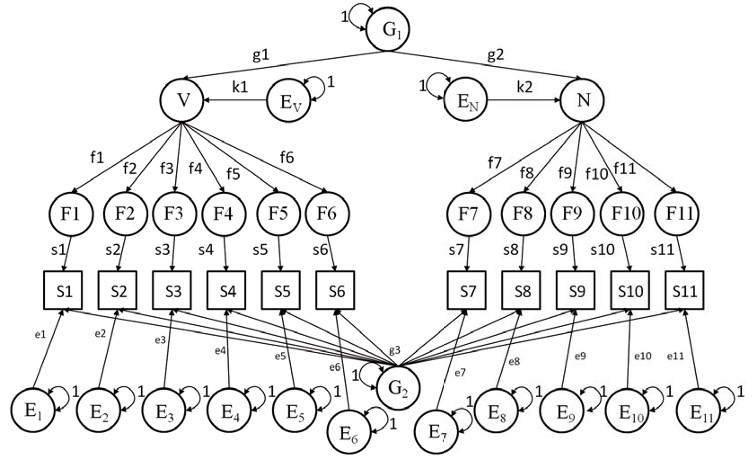
Рис. 6. Мультипликативная модель интеллекта
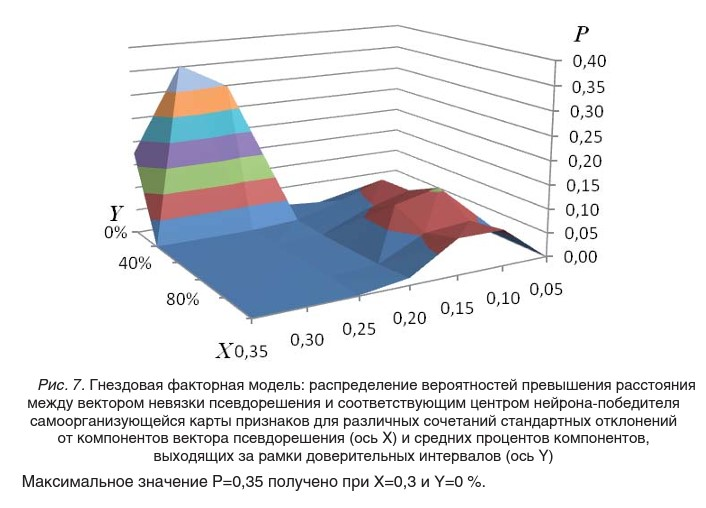
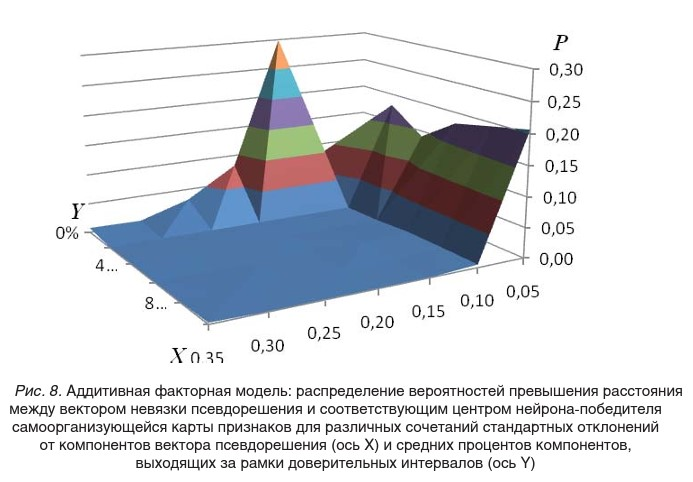
В процессе поиска наиболее оптимальной факторной модели, которая бы одинаково хорошо учитывала влияние генетики и среды, нами была разработана факторная модель, представленная на рис. 5. Она является результатом наложения двух типов моделей: иерархической и гнездовой. Аддитивная модель отличается от иерархической наличием фактора g2. Сравнение иерархической и аддитивной модели позволит определить значимость фактора g2, который отражает влияние генетики на интеллектуальные способности.
Факторная модель, представленная на рис. 6, является результатом наложения двух типов моделей: иерархической и гнездовой, а также добавления ряда специальных факторов, связанных со средовым влиянием на интеллектуальные механизмы, оцениваемые соответствующим субтестом.
Таблица
Оценка вероятности пребывания решения в интервале [m2;m1=1] для аддитивной и гнездовой модели
|
|
0% |
20% |
40% |
60% |
80% |
100% |
|
Ф^) |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
Ф(1) |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
0,5 |
|
P(m2< X < 1) |
0,50 |
0,50 |
0,50 |
0,50 |
050 |
0,50 |
Из таблицы видно, что рассчитанная вероятность для всех доверительных интервалов равна 0,5, что говорит о значимости различий между сравниваемыми моделями. Следовательно, можно сделать вывод, что аддитивная модель согласуется с наблюдениями значимо лучше, чем гнездовая модель при уровне значимости 0,05.
Применение нового метода оценки степени адекватности факторных моделей интеллекта, а также нового метода выявления значимости различий между исследуемыми моделями позволило проанализировать модели путевых коэффициентов, обладающих нелинейной структурой, не проводя процедуру проверки многомерной нормальности распределения наблюдаемых параметров, а также оценить адекватность моделей с заданной степенью точности путем соответствующего увеличения объема генерируемых случайных выборок компонентов псевдорешения. В ходе проведенного исследования было выявлено, что иерархическая модель показала наилучшее соответствие наблюдаемым параметрам (с учетом числа свободных параметров), по сравнению с другими рассмотренными моделями, что говорит о том, что механизм влияния генетики и среды на интеллектуальные способности имеет сходную структуру.
Основные результаты и выводы
Для оценки степени адекватности факторных моделей наблюдениям предложен новый подход, опирающийся на метод Монте-Карло и возможности самоорганизующихся карт Ко- хонена. Он позволяет избежать жестких ограничений, налагаемых на вероятностные распределения результатов наблюдений, которые присущи традиционной процедуре идентификации свободных параметров факторных моделей.
Преимуществами этого подхода являются:
применимость для произвольных факторных моделей без взаимных влияний между переменными, образующих контуры обратной связи;
отсутствие ограничений, налагаемых на распределения наблюдаемых переменных и компонентов вектора невязки (для которых ранее требовалось проверять соответствие многомерному нормальному распределению);
наличие простой процедуры оценки вероятностей появления статистических ошибок 2-го рода;
возможность выявления наиболее правдоподобных сочетаний достигнутой точности идентификации и структуры значимых погрешностей в определении компонентов полученного псевдорешения;
возможность получения оценок адекватности моделей с заданной степенью точности путем соответствующего увеличения объема генерируемых случайных выборок компонентов псевдорешения.