Введение
Одним из естественных функционалов качества управления является время, затрачиваемое системой на достижение заданного терминального состояния. На практике полученная задача оптимального управления называется задачей быстродействия. Существенно, что задача быстродействия для линейных дискретных систем обладает рядом серьезных отличий от аналогичной задачи для непрерывных систем. В то время как в случае непрерывного времени решение, полученное на основе принципа максимума Понтрягина [Понтрягин, 1969] для линейной системы, гарантирует релейный характер оптимального по быстродействию управления, аналогичные системы с дискретным временем [11, 12] в силу дискретного характера функционала качества предполагают принципиально иные критерии оптимальности.
Рассмотрение условий оптимальности процесса при использовании различных классических подходов приводит к двум принципиально отличающимся методам формирования оптимального управления. Метод динамического программирования Беллмана [Беллман, 1960] позволяет построить оптимальное управление в позиционной форме. В случае, когда множество допустимых значений управления представляет собой многогранник, вычисление каждого управляющего воздействия сводится к решению задачи линейного программирования [Ибрагимов, 2021]. Также в [Ибрагимов, 2021] продемонстрирован метод формирования оптимального управления в случае произвольных выпуклых ограничений на управление, основанный на проведении полиэдральной аппроксимации [Каменев, 2010]. Такой подход обладает рядом недостатков, связанных в основном с вычислительными сложностями. Повышение точности гарантирующего решения в задаче быстродействия достигается за счет наращивания числа вершин полиэдральной аппроксимации, что в итоге приводит к экспоненциальному росту сложности соответствующих задач линейного программирования. По этой причине данный подход при реализации на стандартных вычислительных устройствах отличается либо малой точностью решения, либо сравнительно небольшим временным горизонтом особенно для систем большой размерности.
Напротив, сочетание условий оптимальности с дискретным принципом максимума [10-12] позволяет формировать оптимальное программное управление
[Ибрагимов, 2017]. Однако существенным условием применимости данных методов является строгая выпуклость множества допустимых значений управления. С другой стороны, соотношение для начального состояния сопряженной системы в случае произвольной структуры ограничений на управление довольно трудно разрешить. В
[Ибрагимов, 2017а] представлен частный случай эллипсоидальной структуры множества допустимых значений управления, а также аналитическое решение задачи быстродействия для такой системы на основе необходимых и достаточных условий оптимальности, представленных в
[Ибрагимов, 2017].
Естественным подходом является объединение идей построения гарантирующего решения из
[Ибрагимов, 2021] на основе проведения эллипсоидальной аппроксимации множества допустимых значений управления в сочетании с методами формирования программного управления согласно принципу максимума [4, 7]. Методика эллипсоидальной аппроксимации широко распространена в теории оптимального управления [19, 13]. Однако класс эллипсоидов не позволяет добиться произвольной точности аппроксимации исходного множества, а следовательно, и точности решения задачи оптимального управления. С другой стороны, класс суперэллипсоидальных множеств [14, 15] допускает большой порядок точности при сохранении условий строгой выпуклости, что гарантирует простоту решения поставленной задачи аналогично
[Ибрагимов, 2017а].
Целью данной работы является разработка метода формирования оптимального управления в явном виде для случая суперэллипсоидальной структуры множества допустимых значений управления, а также описание подхода построения суперэллипсоидальной аппроксимации произвольного выпуклого тела с максимально возможной точностью на плоскости. Принципиальным отличие от известных результатов по данной тематике [16-18] является рассмотрение произвольного векторного управления, на значения которого наложены выпуклые ограничения.
Постановка задачи
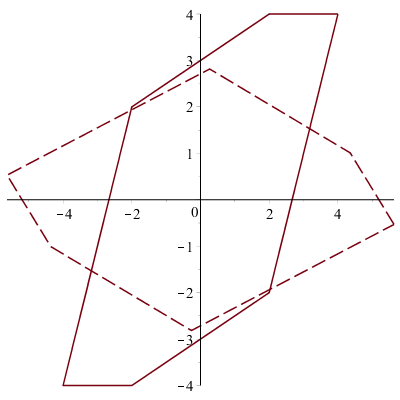
Рис. 1. Исходное множество U (непрерывной линией) и ориентированное B^(-1) U (пунктирной линией)
Рис. 2. Исходное множество U (непрерывной линией) и ориентированное B^(-1) U (пунктирной линией)
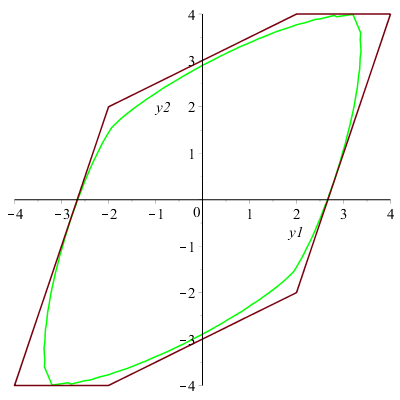
Рис. 3. Исходное множество U и ориентированный суперэллипс B^(-1) E_(4/3) (a)
Заключение
В разделе 2 описана постановка задачи быстродействия и задачи аппроксимации. В разделе 3 рассматривается приведение сложноразрешаемых условий из принципа максимума к суперэллипсоидальной структуре ограничений, которую можно разрешить аналитически. В разделе 4 представлена внутренняя суперэллипсоидальная аппроксимация выпуклого тела, в частности рассмотрены подбор матрицы поворота суперэллипса, параметров суперэллипса, которые определяют форму и размеры суперэллипса. В разделе 5 приведен пример решения задачи быстродействия на основе доказанных утверждений.
Разработанные в статье методы могут быть использованы для проведения численных симуляций и моделирования динамики различных технических и естественных систем. Низкая сложность формирования программного управления и построения оптимальных процессов на основе принципа максимума позволяет как решить задачу быстродействия для заданного начального состояния, так и за приемлемое машинное время накопить большой объем модельных данных и различных траекторий для дальнейшего анализа системы. С другой стороны, аппарат суперэллипсоидальных аппроксимаций гарантирует большую точность в сравнении с классическими эллипсоидальными аппроксимационными методами.