Сравнительный анализ эффективности использования метаэвристических методов моделирования для решения задачи коммивояжёра

Н.В. Кошуняева; А.Г. Тутыгин

doi:10.17759/mda.2025150305

Введение

Задача коммивояжёра (TSP — Traveling Salesman Problem) является одной из классических NP-трудных задач комбинаторной оптимизации, имеющая широкое практическое применение в логистике, транспортном планировании, биоинформатике и других областях (Applegate et al., 2006; Karp, 1972). Её суть заключается в поиске на графе кратчайшего замкнутого маршрута, проходящего через все заданные пункты с возвратом в исходную точку. Точное решение TSP для большого числа вершин становится вычислительно неосуществимым из-за экспоненциального роста сложности. Это обуславливает актуальность разработки и сравнительного анализа метаэвристических методов, позволяющих находить приближённые решения с приемлемой точностью за разумное время (Blum, Roli, 2003).

Среди множества метаэвристик особый интерес представляют алгоритмы, основанные на природных системах: муравьиный алгоритм (ACO — Ant Colony Optimization), алгоритм роя частиц (PSO — Particle Swarm Optimization) и алгоритм имитации отжига (SA — Simulated Annealing). Они демонстрируют высокую эффективность в решении сложных оптимизационных задач благодаря способности балансировать между исследованием пространства решений и эксплуатацией найденных локальных оптимумов (Bonabeau, Dorigo, Theraulaz, 1999; Kirkpatrick, Gelatt, Vecchi, 1983).

Муравьиный алгоритм, основанный на поведении колоний муравьёв, использует механизм феромонных следов для накопления информации о качестве решений (Штовба, 2003; Colorni, Dorigo, Maniezzo, 1991). Алгоритм роя частиц имитирует коллективное поведение стай птиц, где каждая частица адаптирует свою траекторию на основе личного и группового опыта (Kennedy, Eberhart, 1995). Алгоритм имитации отжига, заимствованный из металлургии, применяет вероятностный подход для выхода из локальных минимумов (Kirkpatrick, Gelatt, Vecchi, 1983). Несмотря на обширные исследования этих методов (например, (Иванов, Смирнова, 2021; Попов, Соколов, 2019)), их сравнительная эффективность для TSP остаётся предметом дискуссий, особенно при увеличении размерности задачи.

Целью данной работы является сравнительный анализ эффективности трёх метаэвристических алгоритмов — ACO, PSO и SA — для решения классической задачи коммивояжёра. В рамках исследования:

Проведена параметрическая настройка каждого алгоритма для задачи со 100 пунктами.
Оценена сходимость методов на основе длины найденного маршрута и числа итераций.
Выявлены оптимальные комбинации параметров для каждого из этих алгоритма.

Гипотеза исследования заключается в том, что муравьиный алгоритм, благодаря механизму положительной обратной связи через феромоны, обеспечит более высокую точность решения по сравнению с PSO и SA, но требует больше вычислительных ресурсов.

Научная новизна работы заключается в комплексном экспериментальном сравнении алгоритмов на идентичных тестовых данных с акцентом на влияние параметров на результат. Практическая значимость связана с рекомендациями по выбору метода для задач маршрутизации в реальных условиях, таких, как планирование логистических цепей в условиях севера и Арктики (Иванов, 2021; Тутыгин, Антипов, Коробов, 2020).

Исследование опирается на работы отечественных и зарубежных авторов, включая (Dorigo et al., 2021; Попов, Соколов, 2019; Hussien et al., 2022), а также собственные вычислительные эксперименты. Результаты представлены в сравнительных таблицах и визуализированы для наглядности.

Постановка задачи коммивояжёра

Задача коммивояжёра относится к классу NP-трудных комбинаторных оптимизационных задач. Для построения модели задачи коммивояжёра зададим множество пунктов

V = {v_{1}, v_{2}, \dots, v_{n}}

и матрицы расстояний

D = (d_{i j})

, где

d_{i j}

– стоимость перехода из пункта

v_{i}

в пункт

v_{j}, i, j = \bar{1, n}

. Требуется найти такой замкнутый маршрут (гамильтонов цикл) минимальной длины, который проходит через каждый пункт ровно один раз и возвращается в исходную точку (Applegate at al., 2006). Целевая функция задаётся следующим образом:

L (π) = \sum_{i = 1}^{n - 1} d_{π (i),} d_{π (i + 1)} + d_{π (n),} d_{π (1)} \to \min,

где π — перестановка пунктов, задающая порядок их посещения.

В случае полного неориентированного графа общее число различных гамильтоновых циклов составляет

(n - 1)! / 2

. Это делает точные методы решения задачи неэффективным уже для

n \geq 20

(Karp, 1972). В отличие от точных методов, требующих экспоненциальных вычислительных ресурсов, современные метаэвристические алгоритмы позволяют находить приближённые решения задачи коммивояжёра за полиномиальное время (Talbi, 2021).

В работе рассматривается евклидова задача коммивояжёра размерности

n = 100

, в которой координаты вершин генерируются случайным образом в единичном квадрате, а расстояния между ними вычисляются как евклидова норма в декартовой системе координат.

Для решения поставленной задачи выбраны три метаэвристических метода: метод имитации отжига, муравьиной колонии, роя частиц.

Решение задачи коммивояжёра алгоритмом имитации отжига

Алгоритм имитации отжига (SA) (Kirkpatrick, Gelatt, Vecchi, 1983) основан на аналогии с термообработкой металлов. Атомы при нагревании покидают свои позиции в кристаллической решётке, а при последующем охлаждении стремятся занять положения с минимальной энергией. Важной особенностью процесса является возможность временного перехода в состояния с более высокой энергией, что предотвращает застревание в локальных минимумах.

Современные исследования (Tsotskas, Kipouros, 2022; Zhang et al., 2020) подтверждают значимость метода имитации отжига среди эффективных эвристик для решения задачи коммивояжёра. Алгоритм показывает наилучшие результаты на задачах средней размерности (Johnson et al., 1989). Приведём SA для решения задачи коммивояжёра со 100 пунктами с нормализованными координатами из единичного квадрата:

Шаг 1. Задаём параметры задачи (генерируем

n = 100

пунктов с координатами из промежутка

(0; 1)

, расстояние между которыми рассчитывается по евклидовой метрике) и параметры алгоритма (Тmax – начальную температуру, α – коэффициент охлаждения, Тmin –минимальную температуру, i_max – максимальное количество итераций).

Шаг 2. Находим начальное решение (x_current) – случайный маршрут с посещением всех пунктов, вычисляем энергию - длину пути (E_current).

Шаг 3. Основной цикл – метод имитации отжига. Начиная с самого высокого значения температуры (Тmax) производим вычисления, пока T > Тmin и не достигнуто i_max итераций.

Шаг 3.1. Генерируем новое решение (x_new) путём случайной перестановки двух пунктов в маршруте.

Шаг 3.2. Вычисляем изменение энергии – длины пути:

∆ E = E_{new} - E_{current}

. Если

∆ E \leq 0

, то принимаем новое решение. Если

∆ E > 0,

то принимаем новое решение с вероятностью

p = e^{- ∆ E / T}

.

Шаг 3.3. Обновляем лучшее решение, понижаем температуру.

Шаг 4. Сохраняем лучшее найденное решение, визуализируем результаты.

Реализация алгоритма была произведена с использованием языка программирования python. В качестве визуализации решения представляется график сходимости результатов и граф найденного лучшего маршрута. При значениях параметров

n = 100

,

T \max = 1000

,

α = 0,0003

,

T \min = 1

,

i_{\max} = 100000

, длина лучшего найденного маршрута оказалась равной 45.2, которая была достигнута на 23000 итерации. Визуализация результата представлена на рис. 1.

Рис. 1 — Рис.1. Результат решения задачи коммивояжёра со 100 пунктами методом имитации отжига

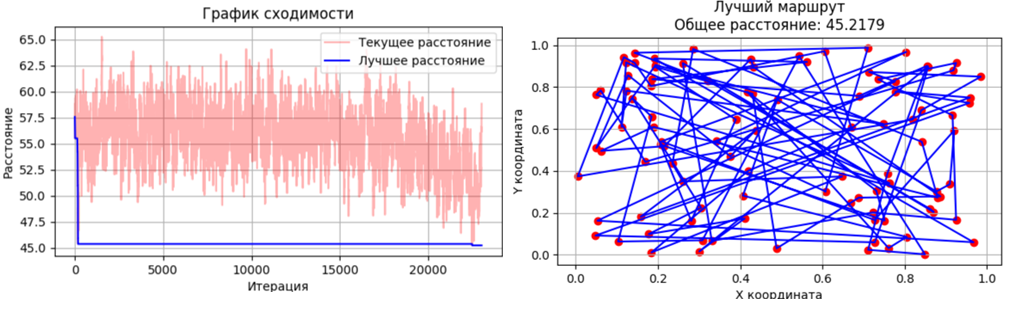
Fig.1. The result of solving the traveling salesman problem with 100 points by simulated annealing

Решение задачи коммивояжёра алгоритмом муравьиной колонии

Муравьиный алгоритм (ACO), разработанный М. Дориго в 1990-х годах (Dominguez, Cannella, 2020), относится к природным вычислениям. Он моделирует поведение муравьёв, оставляющих феромоновые следы для нахождения оптимальных путей. В вычислительной реализации каждый «муравей» строит решение задачи коммивояжёра, выбирая следующий пункт на основе уровня феромона и расстояния. ACO эффективен для задач средней размерности благодаря параллелизму, устойчивости к локальным оптимумам и масштабируемости. Приведём алгоритм ACO для решения задачи коммивояжёра со 100 пунктами с нормализованными координатами из единичного квадрата.

Шаг 1. Задаём параметры задачи (генерируем

n = 100

городов с координатами из промежутка

(0; 1)

, расстояние между которыми – матрица расстояний, рассчитывается по евклидовой метрике) и параметры алгоритма (m – количество муравьёв, τ – матрица феромонов, проинициализированная малыми значениями τ₀, α – параметр, задающий влияние феромона, β – параметр, задающий влияние эвристики, ρ – параметр, задающий интенсивность испарения феромона, Q – коэффициент усиления феромона, i_max–максимальное количество итераций).

Шаг 2. Размещаем муравьёв по вершинам.

Шаг 3. Основной цикл – метод муравьиной колонии, выполняем, пока не достигнуто i_max.

Шаг 3.1. Для каждого муравья выполняем цикл по количеству вершин в графе. Для текущей вершины вычисляем вероятность перехода в каждую следующую непосещённую вершину по формуле:

P_{ij} = \frac{τ_{ij}^{α} η_{ⅈj}^{β}}{\sum_{m \in A} τ_{ℑ}^{α} η_{ℑ}^{β}}

, где

τ_{ij}

– количество феромона между вершинами

i

и

j

,

η_{ij}

– эвристическая информация, A – множество вершин, ещё не включенных в маршрут. Следующую вершину для посещения выбираем с учётом рассчитанной вероятности и добавляем её в маршрут муравья. После посещения муравьём всех вершин запоминаем полученное решение.

Шаг 3.2. После сравнения всех найденных решений муравьями, находим лучшее решение и обновляем лучший маршрут и минимальную длину пути.

Шаг 3.3. Изменяем количество оставшегося феромона на рёбрах графа, то есть обновляем феромонную матрицу по следующей формуле:

τ_{ij} \leftarrow τ_{ij} ∙ (1 - ρ) + Q / L_{k}

, где Lk — длина маршрута k-го муравья.

Шаг 4. Выводим лучший маршрут и его длину, визуализируем результат.

Реализация алгоритма была произведена с использованием языка программирования python. В качестве визуализации решения представляется график сходимости результатов и граф найденного лучшего маршрута. При значениях параметров

n = 100

,

α = 0,5

,

β = 3,5

,

ρ = 0,3

, длина лучшего найденного маршрута оказалась равной 9.23, которая была достигнута на 98-й итерации. Визуализация результата представлена на рис. 2.

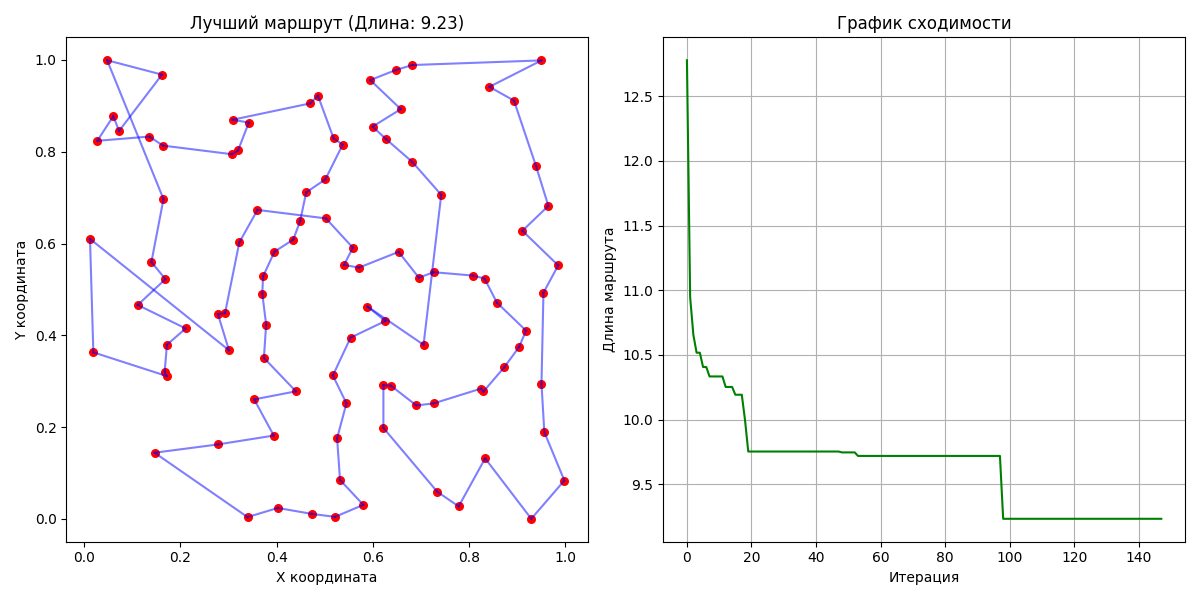
Рис. 2 — Рис.2. Результат решения задачи коммивояжёра со 100 пунктами методом муравьиной колонии

Fig.2. The result of solving the traveling salesman problem with 100 points using the antcolony method

Решение задачи коммивояжёра алгоритмом роя частиц

Метод роя частиц (PSO) представляет собой мультиагентный алгоритм оптимизации, в котором множество взаимодействующих частиц совместно исследуют пространство решений. Разработанный Кеннеди и Эберхартом (Bonabeau, Dorigo, Theraulaz, 1999) на основе идей Рейнольдса, он моделирует движение частиц, которые корректируют свою скорость и положение, ориентируясь на личный лучший результат и лучшее решение всей группы. Алгоритм эффективно исследует пространство поиска, сходясь к оптимуму (Попов, Соколов, 2019). Приведём алгоритм PSO для решения задачи коммивояжёра со 100 пунктами с нормализованными координатами из единичного квадрата.

Шаг 1. Задаём параметры задачи (генерируем

n = 100

городов с координатами из промежутка

(0; 1)

, расстояние между которыми – матрица расстояний, рассчитывается по евклидовой метрике) и параметры алгоритма (с1 – когнитивный коэффициент, с2 – социальный коэффициент, w – инерционный вес, i_max – максимальное количество итераций, создаём m – частиц, где каждая представляет xcurrent – текущий случайный маршрут, v – скорость, подразумевающая список перестановок пар пунктов, xk – копия лучшего личного решения, Lk – длина лучшего личного решения).

Шаг 2. Определяем лучший маршрут (xbest) среди всех частиц и его длину (Lmin).

Шаг 3. Основной цикл – метод роя частиц, выполняем, пока не достигнуто i_max.

Шаг 3.1. Обновляем скорости частиц по формуле:

v_{current} \leftarrow w ∙ v_{current} + c_{1} ∙ r \land () (x_{k} - x_{currunt}) + c_{2} ∙ rand () (x_{best} - x_{currunt})

, где (rand() — случайное число из [0,1])

Шаг 3.2. Обновляем положение частицы:

x_{current} \leftarrow x_{current} ∙ v_{current}

Шаг 3.3. Вычисляем Lk и Lmin. Если найденные личное и глобальное решения лучше, то обновляем их.

Шаг 4. Выводим лучший маршрут и его длину, визуализируем результат.

Реализация алгоритма была произведена с использованием языка программирования python. В качестве визуализации решения представляется график сходимости результатов и граф найденного лучшего маршрута. При значениях параметров

n = 100

;

c_{1} = 1,6

;

c_{2} = 0,8

;

w = 0,4

, длина лучшего найденного маршрута оказалась равной 32.64, которая была достигнута на 92-й итерации. Визуализация результата представлена на рис. 3.

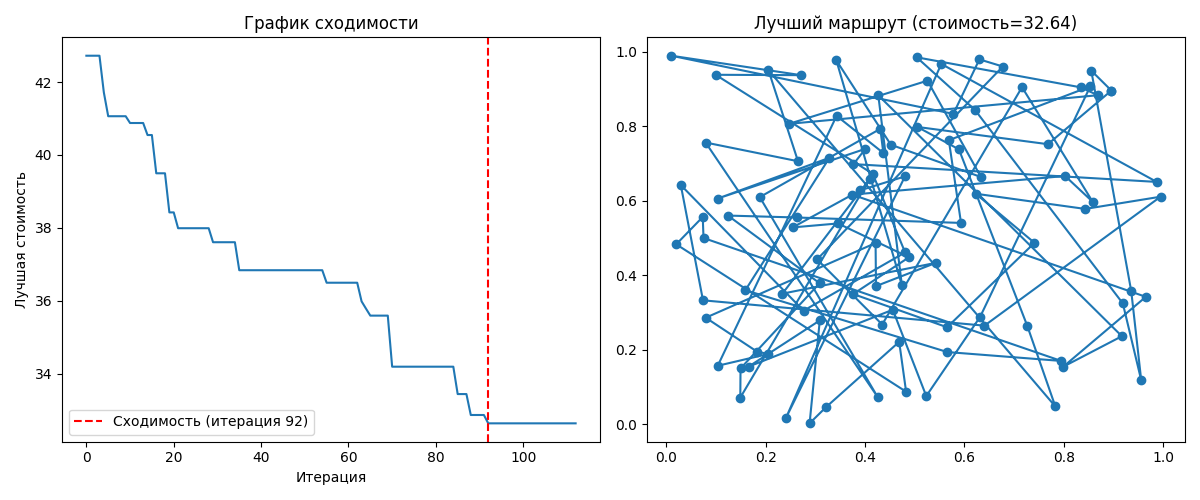
Рис. 3 — Рис.3. Результат решения задачи коммивояжёра со 100 пунктами методом роя частиц

Fig.3. The result of solving the traveling salesman problem with 100 points by the particles warm method

Результаты вычислительных экспериментов

Для определения оптимальных параметров алгоритмов проведена серия вычислительных экспериментов с варьированием ключевых коэффициентов каждого метода.

В параметрических экспериментах при решении задачи коммивояжёра с использованием метода PSO варьировались коэффициент начальной температуры Тmax и коэффициент охлаждения α. Полученные результаты представлены в табл.1. В правом верхнем углу каждой ячейки указан номер шага сходимости алгоритма, а в нижнем левом углу – значение длины найденного маршрута.

Таблица 1 / Table 1. Решение задачи коммивояжёра методом имитации отжига Solving the traveling salesman problem by simulated annealing

Тmax

α

1000

800

600

400

200

100

0,001

6000

41,72

6000

40,61

6000

43,34

5000

45,83

5000

42,55

4000

46,58

0,0008

8000

44,89

8000

43,45

7000

42,9

7000

39,32

6000

42,08

5000

44,73

0,0006

11000

44,56

11000

44,51

10000

41,59

9000

41,78

8000

43,02

7000

39,42

0,0004

17000

42,65

16000

42,10

15000

45,13

14000

41,51

13000

39,46

11000

44,36

0,0002

34000

40,17

33000

42,90

31000

40,81

29000

41,27

26000

40,72

43000

44,51

0,0001

69000

40,00

66000

41,42

63000

41,48

59000

39,69

52000

40,69

46000

42,09

Анализируя полученные результаты, можно сделать выводы о том, что с понижением начальной температуры алгоритм быстрее сходится к оптимальному решению: чем выше значение скорости охлаждения, тем меньше итераций требуется для получения итогового значения; значения длин маршрутов варьируется от 39,32 до 46,58.

В параметрических экспериментах при решении задачи коммивояжёра с использованием метода ACO варьировались коэффициенты α – значимость феромона, β – значимость расстояния и ρ – интенсивность испарения феромона. Полученные результаты представлены в табл.2. В правом верхнем углу каждой ячейки указан номер шага алгоритма, а в нижнем левом – значение длины найденного маршрута. Серым цветом выделены ячейки с полученной длиной маршрута меньше 9.00.

Таблица 2 / Table 2

Решение задачи коммивояжёра методом муравьиной колонии

Solving the traveling salesman problem by the ant colony method

ρ=0,3

β

α

0

0,5

1

1,5

2

2,5

3

3,5

0

44

45,08

175

35,83

22

30,35

108

22,29

8

17,43

56

12,34

53

11,48

16

11,00

0,5

58

45,36

71

28.03

49

16.23

46

11,78

75

10,71

72

9,78

74

9,35

98

9,23

1

43

42,18

45

12,07

28

10,38

73

9,11

114

8,01

95

8,68

175

8,29

87

7,95

1,5

74

44,94

41

8.91

33

8,59

27

8,94

54

8,79

5

8,38

24

8,14

55

8,15

2

1

42,17

51

10,83

12

9,07

6

9,54

25

7,98

11

8,67

21

8,21

6

8,80

2,5

1

45.06

6

13,62

5

9,40

8

7,96

2

8,25

4

8,31

44

8,70

7

8,97

3

1

44,48

6

13,29

16

9,12

14

9,56

16

8,74

3

8,60

8

9,33

5

8,25

3,5

1

43,79

6

14,12

8

10,56

8

8,66

3

8,57

5

8,56

4

9,04

26

8,66

ρ=0,5

β

α

0

0,5

1

1,5

2

2,5

3

3,5

0

117

41,04

444

36,81

181

28,15

100

21,13

395

16,42

30

13,38

95

11,7

66

10,95

0,5

251

43,37

234

28,75

456

42,9

112

12,24

424

9,93

417

8,87

371

8,82

448

7,88

1

456

42,9

332

10,87

485

9,44

458

8,71

190

8,50

66

8,64

44

8.12

25

8.66

1,5

2

43,57

56

9,70

69

8,59

32

8,25

31

8,49

39

8,37

27

8,31

15

8,58

2

49

44,53

37

10,23

27

9,26

18

8,82

17

8,85

20

8,97

5

8,32

3

8,98

2,5

22

45.38

31

10,65

22

8,85

15

8,77

10

9,43

8

8,39

5

8,93

5

8,64

3

25

43,64

22

10,87

18

9,33

13

8,33

5

9,14

3

8,92

8

7,86

8

9,02

3,5

20

44,29

18

11,10

10

9,82

8

8,56

8

8,62

5

8,75

8

8,69

3

8,39

ρ=0,7

β

α

0

0,5

1

1,5

2

2,5

3

3,5

0

93

44,87

74

34,44

70

30,2

23

21,64

25

17,22

17

13,46

10

11,01

6

11,13

0,5

87

44,82

52

22,29

22

14,87

67

11,39

15

10,30

21

9,70

45

8,32

14

9,21

1

108

43,77

51

11,77

88

8,64

111

8,91

61

8,32

23

7,93

65

8.24

30

8.29

1,5

3

45,62

29

9,74

26

8,68

26

8,04

16

8,16

49

7,99

32

8,57

55

8,46

2

1

45,53

21

11,63

10

9,12

21

8,39

10

8,29

3

8,00

20

8,40

10

8,43

2,5

2

46,27

7

13,47

7

9,39

7

9,37

2

9,49

3

9,02

5

8,44

4

8,75

3

2

44,50

4

14,79

8

10,18

19

9,79

5

8,81

3

8,71

3

8,61

15

8,30

3,5

1

44,61

10

16,50

8

9,75

7

9,18

6

9,78

3

9,06

1

8,57

3

8,39

Анализируя полученные результаты, можно сделать вывод о том, что результат работы алгоритма ACO в большой степени зависит от значений входных параметров, значения длины маршрутов находятся в диапазонах от 46,27 (при

ρ = 0,7

,

α = 2,5

и

β = 0

) до 7,86 (при

ρ = 0,5

,

α = 3

и

β = 3

). При нулевом значении параметра видимости (

β = 0

) алгоритм теряет способность учитывать расстояния между пунктами, что приводит к попаданию в локальные оптимумы, значительному ухудшению качества решений, длине маршрутов в диапазоне 41,04 - 46,27 (наихудшие показатели), независимости результатов от значений α и ρ. При

α = 0

(игнорирование феромонов) наблюдается снижение эффективности алгоритма, разброс результатов 10,95 - 45,08, потеря коллективного «опыта» муравьев, преобладание случайного поиска.

Проведенные исследования демонстрируют существенное преимущество муравьиного алгоритма перед методом имитации отжига при решении задачи коммивояжёра. Экспериментальные данные подтверждают, что увеличение параметра видимости β приводит к систематическому снижению длины конечного маршрута. Однако анализ чувствительности алгоритма выявил значительную зависимость результатов от баланса между параметрами α и β – даже незначительные изменения их значений вызывают существенные колебания качества решения. Эта особенность объясняется сложным нелинейным взаимодействием факторов влияния феромонных следов и эвристической информации о расстояниях между пунктами. Наблюдаемая неустойчивость работы алгоритма при нарушении баланса параметров подчеркивает важность их тщательного подбора для каждой конкретной постановки задачи.

В параметрических экспериментах при решении задачи коммивояжёра с использованием метода PSO варьировались параметры w – коэффициент инерции, c1 – когнитивный коэффициент и c2 – социальный коэффициент. Полученные результаты представлены в табл.3. В правом верхнем углу каждой ячейки указан номер шага сходимости алгоритма, а в нижнем левом углу – значение длины найденного маршрута. Серым цветом выделены ячейки с полученной длиной маршрута меньше 30.00.

Таблица 3 / Table 3

Решение задачи коммивояжёра методом роя частиц

Solving the traveling salesman problem by the particle swarm method

w = 0,2

с1

с2

0

0,2

0,4

0,6

0,8

1

1,2

1,4

0

2

48,30

1

46,41

499

45,71

499

44,64

1

45,29

499

49,55

1

46,52

1

45,56

0,2

121

32,55

35

39,44

249

26,98

234

28,33

221

25,20

240

25,51

282

24,18

60

39,82

0,4

93

32,89

83

31,65

81

31,02

87

31,98

115

30,14

132

30,33

120

30,59

150

25,33

0,6

36

33,88

35

32,94

43

31,92

54

30,18

63

31,51

72

30,83

110

27,54

90

27,12

0,8

24

30,67

32

33,87

27

40,79

39

30,47

50

32,89

40

30,42

57

28,48

48

30,33

1

15

34,10

24

29,98

28

31,57

35

28,81

34

30,69

44

31,44

58

30,39

39

28,49

1,2

17

34,57

20

33,22

17

31,41

37

29,81

45

33,32

29

31,63

45

28,01

27

33,43

1,4

12

36,14

17

34,18

17

31,36

26

33,84

18

34,09

29

28,33

40

31,15

50

27,19

w = 0,4

с1

с2

0

0,2

0,4

0,6

0,8

1

1,2

1,4

0

1

48,44

8

43,30

8

49,79

2

49,05

4

43,78

8

46,49

1

46,92

5

50,43

0,2

110

34,04

16

41,96

21

45,32

138

40,68

339

27,95

18

43,55

34

39,46

88

40,27

0,4

40

33,44

144

30,65

175

30,02

198

28,75

29

41,24

50

38,31

171

34,85

53

41,08

0,6

67

34,19

73

30,29

142

31,66

145

29,88

21

39,97

19

38,72

40

41,68

13

43,47

0,8

48

35,92

81

32,42

146

30,19

189

28,87

178

27,06

217

29,98

83

36,06

28

44,67

1

40

31,67

47

34,23

110

27,13

156

29,18

137

29,09

46

36,91

22

40,26

63

33,73

1,2

41

30,76

60

28,39

79

30,57

126

29,14

147

28,95

210

32,07

37

38,98

243

30,95

1,4

35

30,73

44

34,18

62

31,00

86

31,62

154

28,60

212

27,88

302

25,06

152

33,01

w = 0,6

с1

с2

0

0,2

0,4

0,6

0,8

1

1,2

1,4

0

1

44,27

2

44,18

1

47,58

1

47,53

2

45,58

20

43,77

4

47,11

15

47,07

0,2

140

34,08

42

41,35

42

43,47

34

44,16

8

46,54

28

42,75

37

43,68

22

42,13

0,4

152

33,06

85

42,51

23

40,42

22

44,71

64

42,03

10

42,87

42

46,12

40

43,78

0,6

143

32,13

4

42,86

23

44,04

7

45,23

34

45,49

31

43,49

12

45,73

20

41,07

0,8

134

33,09

12

40,33

27

40,79

6

43,17

61

41,96

38

43,48

13

41,98

26

46,11

1

217

31,29

70

41,14

10

45,45

6

45,59

29

43,66

42

45,64

33

46,72

24

41,81

1,2

221

31,09

5

44,29

7

45,53

15

41,73

12

45,28

44

41,5

8

44,43

27

44,34

1,4

181

31,25

45

42,26

17

42,17

8

43,52

18

44,14

4

44,03

27

42,18

499

40,79

Анализируя полученные результаты можно сделать вывод о том, что длина маршрута в зависимости от значений параметров алгоритма варьируется от 24,18 до 49,79; наилучшая сходимость алгоритма наблюдается при значении коэффициента инерции

w = 0,2

и

w = 0,4

.

Экспериментальные данные показывают, что при инерционном коэффициенте

w = 0,6

длина получаемых маршрутов существенно превышает результаты, достигнутые при меньших значениях данного параметра. Такая зависимость свидетельствуето том, что снижение инерции способствует более эффективному исследованию пространства решений и усиливает влияние когнитивного (c1) и социального (c2) компонентов алгоритма. При этом оптимальная производительность достигается при умеренных значениях c1 и c2, которые позволяют избежать преждевременной сходимости к субоптимальным решениям.

Сравнительный анализ продемонстрировал промежуточное положение алгоритма роя частиц по эффективности между методом имитации отжига и муравьиным алгоритмом при решении задачи коммивояжёра. Важно отметить, что для получения качественных решений требуется проведение многочисленных вычислительных экспериментов с различными комбинациями параметров. Однако даже при фиксированных значениях c1 и c2 наблюдается значительная вариативность результатов, что свидетельствует о высокой чувствительности алгоритма к начальным условиям и сложном характере взаимодействия управляющих параметров. Данная особенность подчеркивает необходимость разработки более совершенных механизмов балансировки влияния различных факторов в алгоритме.

Обсуждение результатов

Проведенное сравнительное исследование SA, ACO и PSO для решения задачи коммивояжёра позволило выявить существенные различия в их эффективности. Наибольшую точность продемонстрировал муравьиный алгоритм, который в среднем находил маршруты значительно короче по сравнению с методом имитации отжига и с алгоритмом роя частиц для тестовых примеров размерностью в 100 вершин. Это объясняется способностью ACO эффективно комбинировать положительную обратную связь через феромонные следы с эвристической информацией о расстояниях между пунктами, что обеспечивает устойчивый баланс между исследованием пространства решений и эксплуатацией найденных хороших маршрутов.

Алгоритм роя частиц показал промежуточные результаты, превосходя метод имитации отжига по скорости сходимости, но уступая муравьиному алгоритму по точности конечного решения. Наилучшие показатели PSO наблюдались при относительно низких значениях инерционного веса (

w 0,3 - 0,4

) и умеренных коэффициентах социального и когнитивного влияния (

c_{1} 1,2 - 1,5, c_{2} 1,0 - 1,2

), что подтверждает важность правильного баланса между индивидуальным и коллективным опытом частиц.

Метод имитации отжига, несмотря на простоту реализации, продемонстрировал наименьшую эффективность, особенно заметную при увеличении размерности задачи. При

n > 200

качество решений SA существенно ухудшалось, в то время как ACO и PSO сохраняли приемлемую точность. Это связано с фундаментальным ограничением SA – отсутствием механизма накопления и использования коллективного опыта, что критически важно для задач высокой размерности.

Особый интерес представляют результаты параметрического анализа, выявившие различную чувствительность методов к настройкам. Муравьиный алгоритм показал наибольшую стабильность при вариации параметров в диапазонах

α \in [0.5,1 .5]

и

β \in [2,5]

, в то время как PSO требовал более точной настройки коэффициентов. Это делает ACO более предпочтительным для практического применения, особенно в условиях, когда невозможно проводить многократную тонкую настройку параметров для каждой конкретной задачи.

Полученные результаты согласуются с современными исследованиями в области метаэвристической оптимизации, подтверждая, что для задач комбинаторной оптимизации, подобных TSP, методы, основанные на коллективном интеллекте (ACO, PSO), как правило, превосходят подходы, основанные на индивидуальном поиске (SA). Особую значимость это имеет для морской транспортной логистики Арктического региона, где в условиях высокой неопределенности для принятия решений требуется учет множества динамических факторов и оптимизация сложных маршрутных сетей (пример расчета маршрутов для портов и портопунктов Белого моря приведен авторами в работе (Кошуняева, Тутыгин, 2025)).

Заключение

Сравнительный анализ метаэвристических методов (имитации отжига, муравьиного и роя частиц) подтвердил гипотезу о преимуществе подходов, основанных на коллективном интеллекте, для решения задачи коммивояжёра. Наибольшую эффективность продемонстрировал муравьиный алгоритм, обеспечивающий оптимальный баланс между качеством решений и вычислительными затратами. Это преимущество объясняется эффективным сочетанием механизмов положительной обратной связи через феромонные следы и использования эвристической информации о расстояниях между городами.

Параметрический анализ выявил оптимальные диапазоны значений управляющих коэффициентов для каждого алгоритма. Для муравьиного алгоритма наилучшие результаты достигаются при

α \in [0.5,1 .5]

,

β \in [2,5]

и

ρ \in [0.1,0 .3]

, что подтверждает важность сбалансированного учёта как коллективного опыта (феромоны), так и локальной информации (расстояния). Метод имитации отжига, несмотря на простоту реализации, оказался наименее эффективным, особенно при увеличении размерности задачи, что связано с отсутствием механизмов накопления и использования коллективного опыта.

Полученные результаты имеют практическую ценность для различных областей, включая арктическую морскую транспортную логистику, где требуется устойчивая оптимизация маршрутов в условиях высокой неопределённости.

Сравнительный анализ эффективности использования метаэвристических методов моделирования для решения задачи коммивояжёра

Резюме

Общая информация

Полный текст

Введение

Постановка задачи коммивояжёра

Решение задачи коммивояжёра алгоритмом имитации отжига

Решение задачи коммивояжёра алгоритмом муравьиной колонии

Решение задачи коммивояжёра алгоритмом роя частиц

Результаты вычислительных экспериментов

Обсуждение результатов

Заключение

Литература

Информация об авторах

Вклад авторов

Конфликт интересов

Декларация об этике

Метрики

Просмотров web

Скачиваний PDF

Всего