Развитие теоретического мышления младших подростков в квазиисследовательской деятельности на уроках математики

Современному ученику при освоении таких школьных предметов, как математика, физика и другие теоретические дисциплины, необходимо уметь отыскивать связи между свойствами объекта и возможными способами его преобразования. В. В. Давыдов показал, что эти умения могут развиваться в квазиисследовательской деятельности, проявляющейся в учебной деятельности развивающего обучения как форма воспроизведения способа изложения исследователями результатов своей работы [1]. Это можно назвать квазиисследовательской деятельностью первого типа. В то же время при решении так называемых учебных задач, которые носят теоретический характер, нередко возникают ситуации, когда ребенок вдруг сам открывает и формулирует закономерности строения объекта, самостоятельно делает широкие обобщения относительно изучаемого материала. Этот тип действий можно назвать квазиисследовательской деятельностью второго типа. Такие моменты в учебной деятельности младших школьников возникают стихийно и, как правило, не фиксируются ни учителем, ни самими учениками.

В. А. Гуружапов высказал предположение, что второй тип исследовательской деятельности в начальной школе, который возникает в силу самого содержания развивающего обучения, в подростковом возрасте может специально культивироваться через совершенствование методики обучения, так как содержание предметов теоретических дисциплин в средней школе предполагает широкие обобщения [2].

Перед нами стояла задача организовать квазиисследовательскую деятельность на уроках математики при изучении программного материала и проследить, какое влияние окажет она на развитие теоретического мышления младших подростков.

Для углубленного анализа учебного процесса, его внутренней связи с психическим развитием детей был проведен формирующий эксперимент. При его планировании предполагалось осуществить активное вмешательство в изучаемый процесс развития математического мышления. Мы старались найти разумное соотношение между регулярным изучением курса математики и квазиисследовательской деятельностью второго типа. Эксперимент проводился и 2001/02 учебном году в V классе общеобразовательного учреждения. В экспериментальном классе (Vэ) в начале учебного года обучались 18 человек. Использовался стандартный учебник для V класса (Вилчнкин Н. Я. и др. Математика: Учебник для 5 класса). В соответствии с, учебным планом в неделю проводилось 6 уроков математики. В контрольном классе (Vк) обучались 25 человек. Преподавание велось традиционными методами, по тому же учебнику, с тем же количеством уроков в неделю, опытным учителем с большим стажем педагогической работы.

В начале учебного года были проведены групповой интеллектуальный тест (ГИТ) и исследование развития теоретического мышления на неучебном и математическом материалах по нашей оперативной методике. Средний балл по ГИТ в классах Vэ и Vк составил 75 и 72 соответственно. По U-критерию Манна-Уитни было установлено, что один класс не превосходит другой по уровню интеллекта. Отдельно были сопоставлены результаты по субтесту 2 «Арифметические задачи», диагностирующему сформированность математических знаний и действий, которые усваиваются в процессе обучения, и субтесту 5 «Числовые ряды», проверяющему умение находить логические закономерности построения математической информации. В обоих случаях по U-критерию достоверных различий в результатах обнаружено не было. Обработка результатов исследования теоретического мышления на неучебном и математическом материалах и в целом по всем заданиям статистически значимых различий не выявила.

Описание формирующего эксперимента

В первом полугодии V класса, когда основная часть времени отводится фактически на обобщение изученного в начальной школе, мы включали в уроки задачи, требующие от обучающихся склонности к исследовательской деятельности. Эти задания прямым или косвенным образом были связаны с изучаемым материалом. Приведем пример такой задачи к теме «Отрезок»: «На отрезке отметили 100 различных точек. Сколько всего получилось различных отрезков?» Для успешного решения этой задачи нужно открыть закономерность увеличения числа отрезков с увеличением числа точек, взятых на отрезке. Подобные задачи требовали от обучающихся использования знаний и умений в ситуациях, приводящих к самостоятельным открытиям закономерностей, лежащих в основе их решения.

Во втором полугодии мы стремились организовать квазиисследовательскую деятельность второго типа при изучении новых тем общеобразовательного курса математики. Полугодие начинается с изучения обыкновенных дробей. Подробный анализ различий двух подходов к изучению обыкновенных дробей провели В. В. Давыдов и Ж. Цветкович [5]. Существует общепринятый, господствующий в современных учебниках способ ознакомления обучающихся с дробями, основанный на «наглядной концепции дроби», согласно которой дробь возникает из конкретной реальности — деления вещей, допускающих разделение. Однако исторически и по материальному содержанию дроби имеют только один предметный источник — измерение величин. Такой подход реализован в рамках системы развивающего обучения [3, 4].

В экспериментальном исследовании сделана попытка, опираясь на возникновение дроби в ситуации измерения, ввести обучающихся в понимание дроби как абстракции отношения величин. «Роль этой абстракции весьма велика как при изучении всего курса математики, так и для общего развития теоретического мышления» [5, с. 96].

Отношение величин, выраженное дробью, отражает некоторые реальные свойства вещей, поэтому на первом уроке мы стремились создать ситуацию, требующую преобразования предметных условий задачи.

Приводим стенограмму вводного урока. Вниманию детей были предложены два груза (М₁= 270 г, М₂=70 г), рычажные весы, закрепленные на штативе, набор грузов по 100 г, линейка. Следовало определить, какой из грузов тяжелее и во сколько раз.

Учитель. Первая ситуация следующая. У меня в руках два груза, два предмета: белый и черный. Я попрошу вас взять в руки эти два груза и сказать, какой из них имеет большую массу, какой из них тяжелее и во сколько раз.

Кирилл. Белый тяжелее в 4 раза.

Женя. Белый тяжелее в 5 раз.

Саша. Белый тяжелее в 7 раз.

Владик. Белый тяжелее в 5 раз.

Учитель. Как узнать, кто из сделавших свой прогноз наиболее близко оказался к правильному результату?

Дима. Нужно взвесить на весах.

Учитель. Представим, что у нас нет никаких весов и нет гирь. Есть один способ, с помощью которого можно узнать точно, во сколько раз один груз тяжелее другого.

Владик. Можно узнать, сколько раз маленький груз поместится в большом. (Прикладывает один груз к другому, как если бы это были прямоугольные полоски.) Если маленький груз вокруг большого ставить, то мы примерно точно узнаем сколько.

Максим. А длина, а ширина? Там тоже какие-то остатки могут остаться.

(Понятно, что Владик хотел заменить сравнение масс сравнением объемов. Поэтому учитель предлагает сравнить два груза одинакового объема, но разной массы.)

Учитель. Как вы думаете, какой из грузов тяжелее?

Владик. Они одинаковые.

Учитель. Потрогай.

Владик. Один тяжелее другого.

Учитель. Во сколько раз?

Владик. Раз в 5.

Учитель. Подходит твой способ для этих грузов?

Владик. Нет.

Учитель. Почему?

Владик. Один сделан из легкого металла, другой — из тяжелого.

Максим. Они могут быть сделаны из одного материала, но в одном внутри ничего нету, а в другом — материал внутри.

После нескольких попыток определить отношение масс «на глаз» и предложения взвесить грузы, т. е. после принятия обучающимися задачи, демонстрировался принцип работы рычажных весов. Предлагалось уравновесить весы, если на одной стороне закреплен груз в 100 г., а на другой — 200 г.

Учитель. Я нам хочу, показать другую идею. Если мы возьмем два одинаковых груза и подвесим их к носам, то весы будут в равновесии. А если я на одну сторону подношу два груза, смогу ли я эти два груза уравновесить на этих весах?

Дети. Да, на другую сторону груз подвесить.

Учитель. А если ничего не подвешивать?

Владик. Нужно подвинуть два груза на середину. (Двигает, весы находятся в равновесии.)

Учитель. Весы снова находятся в равновесии, хотя на одной стороне у нас груз в 100 г, а на другой в 200 г. А задача у нас: во сколько раз белый груз тяжелее черного?

Ученики легко нашли способ решения, предложив сдвинуть второй груз на середину плеча.

Женя. Надо с одной стороны подвесить белый груз, а с другой — черный и к черному грузу подвешивать,

Учитель. У нас больше ничего нет. Только белый и черный грузы.

Владик. Надо эту доску расчертить на деления по весу. Разделить на деления. Допустим, тут 0, тут один груз, тут дна груза.

Женя. А как надо делить? У нас есть только два груза.

Максим. Может быть, надо сначала взвесить белый груз с этими квадратиками (грузами по 100 г). Узнать, сколько квадратиков будет равно этому белому. Потом также узнать, сколько квадратиков в черном грузе.

Учитель. Получится, что мы будем использовать весы с гирями. Попробуй.

Максим (берет черный груз, пытается его взвесить, получается меньше 100 г. Двигает груз в 100 г к центру). Примерно получается 50 г.

Учитель. Как ты это узнаешь?

Максим. В квадратике 100 г. Если другой груз поставить на середину, то получится 50 г. А у нас немного дальше середины, значит, будет примерно 60 г. Теперь взвесим белый груз. Три груза по 100 г уравновешивают белый груз, но при этом белый груз приходится пододвинуть немного ближе к центру.

(Интуитивно Максим объявляет массу большого груза — 280 г.)

Максим. Потом надо 280 разделить на 60, получится примерно 4 раза.

Учитель. Будет получаться число между 4 и 5. Максим попытался взвесить грузы, используя имеющиеся гирьки. Давайте вернемся к ситуации, когда у нас нет никаких гирь и нужно узнать, во сколько раз белый груз тяжелее черного груза.

Владик. Может быть, сначала повесить на один конец черный груз, а на другой конец — белый груз и попытаться с помощью передвижения белого груза уравновесить черный груз, деля пополам расстояния?

(Владик уравновешивает грузы.)

Женя. Нужно измерить расстояние от центра до точки, где висит груз.

(Женя измеряет, получает 5 см. Затем измеряет длину всего плеча, получает 22 см.)

Максим. Примерно получается больше в 4 раза.

Учитель делает рисунок.

Рис. 1

Учитель. Нам надо было узнать, во сколько раз М₂ больше М₁, найти отношение М₁/М₂ Вы для этого предлагаете найти отношение 22 к 5. Как проверить, действительно ли получится верный ответ? Если мы вернемся к ситуации, когда были подвешены два груза — в 100 г и 200 г — и весы находились в равновесии? Какие расстояния нужно измерить, чтобы убедиться в правильности способа Жени?

(Женя измеряет расстояние от центра до груза 200 г, получает 1.1 см. Затем измеряет длину всего плеча, получает 22 см.)

Учитель. Какой вывод можно сделать?

Рис. 2. Схематичное изображение ситуации из задачи к вводному уроку
по теме «Обыкновенные дроби».

Во сколько раз М₂ больше М₁?

Дети. Во столько, во сколько К₁ больше К₂.

Учитель. М₂/М₁ — это дробь. М₂ — числитель дроби, М, — знаменатель дроби.

Для фиксации найденного отношения были предложены графическое изображение (рис. 2) и буквенная модель: М2/М1=К1/К2.

Найденное отношение, записанное в общепринятом виде M2/M1, отражает некоторые реальные свойства вещей. Далее детям было сказано, что такая запись и называется дробью. М2 — ее числитель, М1 — знаменатель. Для исследования указанного отношения в «чистом виде» классу был предложен ряд вопросов.

Учитель. Что изменится, если увеличить М₂?

Дети. Изменится длина.

Учитель. Какая?

Дети. Уменьшится длина К₂.

Учитель. А если мы М₂  уменьшим?

Дети. К₂  увеличится.

Учитель. Если мы М увеличим?

Дети. К₁ уменьшится. А можно К₂  увеличить.

Таким образом, с помощью буквенной модели были получены некоторые свойства отношения величин. Для конкретизации исходной задачи на уроке была предложена еще одна ситуация. В две прозрачные коробки в форме правильной четырехугольной призмы насыпан горох на одинаковую высоту. Требовалось узнать, во сколько раз объем гороха в одной коробке больше объема гороха в другой коробке, т. е. найти отношение V1/V2.

Задача. Оборудование: две прозрачные коробки в форме правильной четырехугольной призмы, горох.

Учитель. В две коробки насыпан горох, причем насыпан он на одинаковую высоту. Во сколько раз масса гороха в одной коробке больше массы в другой коробке? Чему равно отношение V₁/V₂?

Кирилл. Нужно маленькую коробку поместить в большую. (Сравнивает длины коробок, прикладывая их друг к другу.) У меня получается 2 раза.

Максим. Я не согласен. Здесь есть не только длина, но и ширина, и она тоже разная.

Женя. Нужно измерить длину и ширину каждой коробки. (Измеряет, получает у большой коробки 12 см, у маленькой — 7 см. Рисует вид сверху.)

Если одну коробку вложить в другую (рисует),

 то эти части (1 и 2) составят примерно еще одну коробку, а эта часть (3) — одна четверть примерно. Получается два с четвертью.

Учитель. У Жени получился примерный результат.

Максим. У Жени неправильно нарисовано — неточно получилось.

Владик. Нужно померить площадь коробок, если смотреть на них сверху. 144 см² — площадь большой коробки, 49 см² площадь маленькой коробки. Теперь 144 делим на 4,9 — будет около трех.

Учитель. Способ Владика:

Женя. Можно высыпать горох из маленькой коробки и измерить, сколько раз объем гороха из большой коробки уместится в маленькой.

Учитель. Давайте способом Жени проверим правильность наших расчетов. Пересыпаем горох из большой коробки в маленькую, получаем 3 раза.

В результате обсуждения получили ту же запись, что и в первой задаче:

где S₁ и S₂ — площади оснований коробок.

Таким образом, квазиисследовательская деятельность детей по преобразованию предметных условий задачи привела к раскрытию условий происхождения понятия дроби. Используя возникший образ дроби и лежащую в его основе предметную ситуацию, обучающиеся могли выполнять сравнение, например, таких дробей:

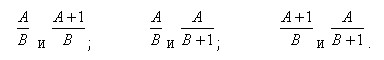
На следующих уроках рассматривалось появление дробей на основе измерения величин. Ученики решали задачи на нахождение дроби от целого и целого по его дроби, определяли место дробей на координатном луче. Здесь мы опирались на разработки, содержащиеся в литературе по развивающему обучению [3, 4, 5].

До введения формальных правил сравнения дробей предлагались различные задания, требующие действия оценки дробей. Например, сравнить 5/215 и 12/13.

Здесь нужно заметить, что 5/215 ближе к нулю, а 12/13 ближе к единице. При сравнении чисел 7/15 и 6/11 возможно рассуждение, основанное на сравнении чисел с половиной: 7/15 немного меньше, а 6/11 немного больше половины. Подобные задания были направлены на развитие ощущения величины дробного числа.

На этапе нахождения дроби от числа ученики нередко сталкивались с ситуацией, когда при одинаковой мерке и разных на вид дробных числах (например, 3/5 и 6/10) получались одинаковые величины. В совокупности этих случаев некоторые дети увидели общий принцип и неожиданно начали использовать его для сравнения дробей с разными знаменателями. Фактически им удалось обобщить закономерность, называемую в математике основным свойством дроби, и выйти на понятие общего кратного. Например, во время устной работы, выполняя задание на сравнение чисел 1/2 и 5/9, задуманное нами для развития чувства дробного числа, один из обучающихся провел следующее рассуждение: «Если бы мы хотели построить величины по числам 1/2 и 5/9, нам было бы удобно взять мерку в 18 клеточек. Тогда первая величина будет из   клеточек, а вторая из   клеточек. Значит, второе число больше». Эту идею сразу подхватили и другие дети, начав подбирать при сравнении двух дробей число, делящееся на оба знаменателя, т. е. отыскивая общее кратное. Продемонстрированный тип действий можно квалифицировать как квазиисследовательскую деятельность второго типа. Мы решили поддержать попытку выхода обучающихся на более высокую образовательную траекторию и предложили задание на обобщение основного свойства дроби (эта тема не входит в программу V класса). Нужно было найти самую большую и самую маленькую дроби в ряду чисел:

(в действительности все числа равны). В результате обсуждения большинством был поддержан способ, согласно которому производилось деление знаменателя каждой дроби на ее числитель. Везде получалось одинаковое частное, а остаток оказывался равен половине числителя. Такой не планируемый нами способ решения возник, вероятно, из сформированного к этому времени восприятия дроби как отношения.

В этом смысле для сравнения не важно, какое отношение находить — меньшего числа к большему или большего к меньшему. После установления равенства всех чисел перед обучающимися был поставлен вопрос о связи между числителями и знаменателями всех дробей. В итоге была получена запись, выражающая основное свойство дроби:

где n — натуральное число.

Целью изучения следующих тем — сложение и вычитание дробей с одинаковыми знаменателями и смешанных чисел — было продолжение формирования чувства дробного числа. До введения формальных правил действий с дробями для устной работы предлагались различные примеры, где требовалось оценить результат, не производя вычислений. Например, 6/11 + 2/3. Дети видели, что каждая из дробей больше половины, поэтому при сложении получится число, большее 1. Некоторые ученики, исходя из знания основного свойства дроби, могли получить точный результат сложения, но специально умение складывать и вычитать дроби с разными знаменателями не отрабатывалось. Заметим лишь, что изложенный выше подход к изучению дробей открывал благоприятные перспективы для освоения новой темы, которая изучается в VI классе. Включение в ходе формирующего эксперимента квазиисследовательской деятельности второго типа в изучение регулярного курса математики показало, что большинство детей готово принимать предлагаемые задачи, включаться в их решение. Результаты влияния организованного таким образом обучения на развитие теоретического мышления приводятся ниже.

Диагностика результатов обучения

Для психологической предметной диагностики результатов обучения была составлена диагностическая работа. Возможность решения заданий проблематизировалась за счет маскировки существенных признаков преобразования объектов несущественными [1]. Для удобства сопоставления результатов за решение каждого задания выставлялось от 0 до 3 баллов. Работа была рассчитана на один урок. Весь текст умещался на стандартном листе бумаги. Все записи решений и ответов предлагалось делать на бланке с заданием, при необходимости можно было использовать обратную сторону листа. Рассмотрим подробнее содержание работы.

Диагностическая работа по математике для V класса по теме «Обыкновенные дроби».

1. Не делая вычислений, попробуйте определить, какое из чисел больше, а какое меньше:

2. Решите примеры. Соедините дугой похожие по способу решения примеры:

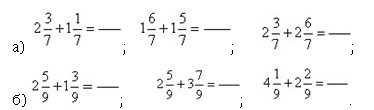
в) Придумайте задание, похожее на 2, б.

3. Решите задачи. Соедините дугой задачи, похожие по способу решения.

а) В букете 15 цветов. Розы составляют 3/5 всех цветов букета. Сколько роз в букете?

б) Розы составляют 2/3 числа всех цветов в букете. Сколько цветов в букете, если роз в нем 6?

в) В шахматы умеют играть 5/8 всех учеников класса. Сколько человек играют в шахматы, если всего в классе 40 учеников?

4. Внимательно прочтите каждый ряд чисел. Обведите число, которое выбивается из закономерности данного числового ряда.

5. Когда прочитали 1/7 всей книги и еще 14 страниц, то остались непрочитанными 28 страниц. Сколько страниц в книге?

Традиционная программа по математике для средней школы определяет основной целью изучения темы «Обыкновенные дроби» в V классе ознакомление учащихся с понятием дроби в объеме, достаточном для введения десятичных дробей. Среди формируемых умений основное внимание должно быть привлечено к сравнению дробей с одинаковыми знаменателями, к сложению и вычитанию целой части числа. С пониманием смысла дроби связаны три основные задачи на дроби, осознанного решения которых важно добиться от учащихся.

Как видно, для успешного выполнения заданий вполне достаточно было знаний и умений, предусмотренных программой. В то же время важно было установить проявление теоретического мышления на материале, изучавшемся в теме «Обыкновенные дроби». Рассмотрим, какие для этого имеются возможности.

В задании 1 только пункт а) можно выполнить, опираясь на формальное правило сравнения дробей с одинаковыми знаменателями. Для сравнения остальных чисел необходимо опираться на существенное исходное отношение, заложенное в определение обыкновенной дроби, иметь своеобразное «чувство» дробного числа, его живой образ. Так, в пункте б) нужно заметить, что число 7/159 ближе к нулю, а 5/6 — к единице.

В пункте в) 7/15 немного меньше, а 5/9 немного больше половины. Для верного решения пункта г) возможно следующее рассуждение: у первой дроби знаменатель меньше, значит, доли более крупные и взято их больше, поэтому первая дробь больше, чем вторая. Решение задания д) опирается на те же соображения.

В решении задания 2 главное внимание должно быть обращено на примеры, которые обучающиеся выделят в качестве похожих. В пункте а) похожими по способу решения являются примеры 2 и 3, где необходимо выделить целую часть в полученных ответах. Этот существенный признак замаскирован несущественными: одинаковыми ответами в примерах 1 и 2 и одинаковыми первыми слагаемыми в примерах 1 и 3. Пункт б) построен аналогично.

В задании 3 в пунктах а) и в) содержатся задачи на нахождение дроби от целого, а в пункте б) — обратная задача, на нахождение целого по его дроби. Как и в задании 2, этот существенный признак спрятан здесь за внешним сходством сюжетов и одинаковыми ответами в задачах а) и б). Выделяя в качестве похожих задачи а) и в), ученик осознает и различает способы решения задач на дроби. Если в качестве похожих ученик выбирает задачи а) и б), это свидетельствует о том, что школьник выделяет и обобщает отдельные лексические единицы текста задачи безотносительно к способу их решения («В этой задаче говорится про розы и в этой про розы, значит, они похожи»).

Для успешного решения заданий 4, а и 4,6 ученик должен понимать, что любая дробь есть число. Тогда в пункте а) он просто увидит ряд чисел: 2, 3, 4, 6, 8, из которых только 3 — нечетное, выпадающее из идущих подряд четных чисел, а в пункте б) — числа 3, 5, 7, 8, 9, 11, из которых 8 не попадает в идущие подряд нечетные числа. В более трудном задании 4,в существенным признаком является одинаковая разность между соседними числами ряда (т. е. перед нами арифметическая прогрессия) и лишним оказывается число 3,3/5. Если ученик обводит число 4, он ориентируется на его внешнюю непохожесть, не вскрывая закономерной связи между другими числами ряда.

Задача 5 включена в работу в качестве резервной. В ней несколько сложнее найти существенное отношение, лежащее в основе способа решения. Анализируя условие, требуется установить, что после прочтения 1/7 всей книги останется прочитать 6/7 книги, или (14+28) страниц. Таким образом, это задача на нахождение целого по его известной дроби.

Результаты диагностики и их обсуждение

После изучения темы «Обыкновенные дроби» обучающимся предлагалась соответствующая диагностическая работа. Результаты по каждому пункту заданий даны в таблице.

Из таблицы видно, что практически по всем заданиям результаты оказались выше в экспериментальном классе. Достоверность различий между процентными долями двух классов оценивалась по критерию j* Фишера. При сравнении процента учащихся Vэ класса с процентом учащихся Vк класса, решивших задания, оказалось, что доля детей, справившихся с заданиями 1(а, б, в, д), 2, а, 3, 4, б, в Vэ классе больше, чем в Vк классе. Более успешное выполнение задания 1 в экспериментальном классе подтверждаем необходимость целенаправленного развития «чувства» дробного числа в процессе обучения. Квазиисследовательская деятельность второго типа, организованная в экспериментальном обучении при введении понятия обыкновенной дроби, позволила обучающимся построить образ обыкновенной дроби, раскрыть понимание существенного исходного отношения, наложенного в определение обыкновенной дроби. В результате три четверти учащихся экспериментального класса успешно справились с заданиями, где знание формального правила сравнения дробей с одинаковыми знаменателями было недостаточно. Несколько более высокие результаты контрольного класса в решении задания 1, г могли получиться за счет тех обучающихся, которые во всех заданиях на сравнение дробей формально применяли правило сравнения дробей, ориентируясь только на числители: 4>3, поэтому и 4/11>3/13. В пункте г) при таком рассуждении ответ случайно оказывался правильным, и отличие от пунктов б) и в).

В задании 2 значимыми получились различия в пункте а), где существенным общим признаком являлось выделение целого из дробной части в полученном ответе. Большинство детей контрольного класса выделяли как похожие примеры 1 и 2 с одинаковыми ответами, ориентируясь на внешние сходства. В пункте б) значимых различий не было получено. Возможно, часть учеников Vэ класса, справившихся с пунктом а), посчитали недостаточным основанием для схожести отсутствие при решении примеров перехода через целую единицу и в пункте б) одинаковые примеры не выделили вообще. Для успешного решения пункта в) необходимо было перейти на более высокий уровень обобщения действий при решении конкретных примеров. Фактически нужно было проанализировать тип самой задачи, сравнивая типы заданий а) и б) или тип задания б) с любыми другими заданиями, состоящими из трех примеров на сложение смешанных чисел. Тогда могло проявиться четкое понимание типа задания б): два примера на сложение без перехода через целую единицу и один пример с этим переходом. Это задание немного труднее предыдущих, и его верное решение позволяет говорить о высоком уровне распознавания и осознания типа сложения. Как видно из таблицы, различий на таком высоком уровне обобщения у детей Vэ и Vк классов при решении примеров достигнуто не было. Несколько другая картина наблюдается при анализе результатов решения задания 3.

В пункте а) задания 3 статистически значимых различий не получилось. Это прямая задача на нахождение дроби от целого. Различия возникли при решении обратной задачи б) на нахождение целого по его дроби, задачи в) и при рефлексии способов решения задач, когда нужно было выделить одинаковые задачи. Ученики Vэ класса смогли выйти на более высокий уровень обобщения при решении задач, чем при решении примеров, распознавая прямую и обратную задачи. Таким образом, дети Vэ класса показали более глубокое проникновение в отношения между величинами, выраженные дробным числом, и понимание существенных оснований своих действий.

Одинаковый уровень успешности выполнения заданий 4, а и 4, б учащимися Vэ класса и «провал» в выполнении задания 4, б учащимися Vк класса позволяют сделать вывод о более устойчивом понимании дроби как отношения чисел в Vэ классе, так как для правильного решения этих заданий требовалось увидеть за дробью отношение между числителем и знаменателем, выраженное в данном задании натуральным числом. В решении более трудного задания 4, в и резервного задания 5 статистически значимых различий не получено.

При решении задания 4,6 из второго варианта работы, где даны, были дроби 27/9; 40/8; 49/7; 48/6; 45/5; 44/4, многие обучающиеся Vк класса обвели число 27/9, ориентируясь на внешний признак: «Во всех числителях есть цифра 4, а в 27/9 нет». Некоторые дети, которые всё же находили отношение, заданное дробью, выделяли в качестве лишнего число 44/4, так как «и остальных случаях при делении получается однозначное число». При этом не вскрывалась закономерность всего ряда — идущие подряд нечетные числа. В задании 4, в наиболее характерным был ответ: «Лишнее число 3, потому что у него нет дроби».

В Vэ классе в задании 4,6 большая по сравнению с Vк классом часть детей сориентировалась на существенный признак построения ряда чисел. Был дан, например, такой ответ: «Если разделить числитель на знаменатель, то получится ряд чисел:

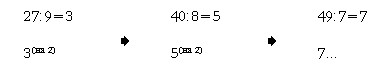
Так получается со всеми дробями, кроме четвертой». Также в Vэ классе были получены два верных решения задания 4, в. Приводим одно из них:

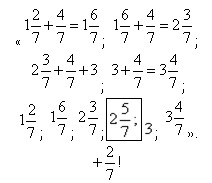
В целом по тесту анализ по U-критерию показал, что различия результатов Vэ и Vк классов статистически значимы (p<0,05). Таким образом, квазиисследовательская деятельность второго типа, организованная при изучении обыкновенных дробей, привела учащихся Vэ класса к более высоким результатам в освоении данной темы.

Выводы

Учащиеся экспериментального класса в сравнении с контрольным показали рост по субтесту «Арифметические задачи» в ГИТ, больший рост по субтесту «Числовые ряды» в ГИТ, лучшие результаты в диагностической работе по теме «Обыкновенные дроби», достоверно больший рост по теоретическому мышлению на математическом материале. У детей в большей мере оказались сформированы чувство дробного числа, рефлексия на способ решения примеров и задач. Полученные данный позволяют сделать вывод о существенном воздействии организованной в процессе формирующего эксперимента квазиисследовательской деятельности второго типа на развитие теоретического мышления младших подростков.

1. Гуружапов В. А. К вопросу о предметной диагностике теоретического мышления детей в развивающем обучении (система Эльконина — Давыдова) // Психологическая наука и образование. 1997. № 4.
2. Давыдов В. В. Теория разминающего обучения. М., 1996.
3. Давыдов В. В., Горбов С. Ф. и др. Математика, 3 класс, 2 о полугодие. М., 1996.
4. Давыдов В. В., Горбов С. Ф. и др. Обучение математике, 3 класс, 2-е полугодие. М., I996.
5. Давыдов В. В., Цветкович Ж. О предметных источниках понятия дроби //: Психологические возможности младших школьников в усвоении математики. М., 1969.