Учет множественности решений задач, направленных на развитие метапредметных компетенций в процессе сценирования учителем учебно-развивающих ситуаций

В 2009 году в Российской Федерации утвержден новый Федеральный государственный стандарт общего начального образования второго поколения, основанный на системно-деятельностном подходе к организации обучения [12]. Такой подход предполагает в организации учебно-воспитательного процесса «переход к стратегии социального проектирования и конструирования в системе образования на основе разработки содержания и технологий образования, определяющих пути и способы достижения социально желаемого уровня (результата) личностного и познавательного развития обучающихся» [там же, с. 3-4]. В качестве образовательных результатов в начальной школе декларируются три типа компетенций - предметные, мета- предметные и личностные. Это требует от учителя принципиально нового уровня психологической подготовки, нежели требовалось в традиционной практике [5; 6; 10]. В частности, ему необходимо обладать достаточной проектной культурой в организации учебного процесса, чтобы выстраивать развивающие учебные ситуации, благоприятные для развития личности и способностей ребенка.

При этом наиболее проблемным моментом в организации учебного процесса является развитие теоретического мышления учащихся, формирование понятий как основы для формирования метапредметных ком­петенций. Поэтому актуальным в настоящее время является вопрос о достижении мета­предметных результатов освоения основной образовательной программы начального общего образования. К ним относятся освоенные детьми универсальные учебные действия (познавательные, регулятивные и коммуникативные), обеспечивающие овладение ключевыми компетенциями, которые составляют основу умения учиться, и межпредметные понятия.

Идеи проектного подхода к организации развивающего учебного процесса в начальной школе достаточно широко представлены в теории и практике системы Эльконина-Да- выдова [2], а также в ряде других развивающих дидактических систем [3; 4; 8; 9]. Обобщая эти достижения, можно утверждать следующее.

1.   Метапредметных образовательных результатов как конкретной формы основ теоретического мышления нельзя достичь простой передачей знаний и душеспасительными беседами - они являются результатом развития ученика в процессе осмысления им содержания учебной деятельности и способа его взаимодействия с другими участниками образовательного процесса.

2.   Деятельность учителя есть, прежде всего, организация коллективной мыслительной работы учащихся, а проектная часть этой деятельности представляет собой сценирование учебно-развивающих ситуаций.

Анализ проблемы формирования мета- предметных компетенций учащихся строился на следующей гипотезе: в основе сценирова- ния учебно-развивающих ситуаций могут лежать способы анализа развивающих возможностей предметных задач и определение вариантов коллективного решения учениками этих задач на уроке.

Определенные предпосылки для этого уже сложились. Дело в том, что за последние два десятилетия идеи развивающего обучения В. В. Давыдова и его последователей нашли отражение в содержании современных программ и методических комплектов начальной школы. Особенно явно это влияние проявилось в программах обучения младших школьников математике. Учебно-методические комплекты насыщены заданиями, связанными с отображением объектов в математических моделях, а следовательно, на их основе можно развивать такие метапредметные компетенции, как «умение анализировать условия адекватности отображения свойства объекта в его модели» и др.

Однако, как показал наш опыт экспертизы учебного процесса, учителя крайне редко используют эти задачи именно в развивающем контексте. Прежде всего, им трудно дается понимание множественности решений развивающих задач. Они не связывают действие моделирования с возможностью разных вариантов соотношения объекта и его модели.

В качестве первого примера рассмотрим представленную на рис. 1 задачу из широко распространенного в России учебника математики, созданного авторским коллективом М.И. Маро с соавторами [7, с. 62].

Ученикам нужно в пустые клеточки поставить числа, отражающие увеличение или уменьшение числа ласточек, сидящих на проводе. На содержании этого задания можно формировать у учащихся такие метапредметные образовательные результаты, как «использование знаково-символических средств представления информации для создания моделей изучаемых объектов и процессов, схем решения учебных и практических задач». Но для этого не следует торопиться с заполнением пустых клеточек конкретными цифрами. Надо сначала проанализировать с детьми связь смысла сюжетной картинки и предлагаемых моделей. Проблема в том, как сформулировать ученикам задачу и организовать ее решение. Рассмотрим возможные варианты.

Ученикам нужно в пустые клеточки поставить числа, отражающие увеличение или уменьшение числа ласточек, сидящих на проводе. На содержании этого задания можно формировать у учащихся такие мета- предметные образовательные результаты, как «использование знаково-символических средств представления информации для создания моделей изучаемых объектов и процессов, схем решения учебных и практических задач». Но для этого не следует торопиться с заполнением пустых клеточек конкретными цифрами. Надо сначала проанализировать с детьми связь смысла сюжетной картинки и предлагаемых моделей. Проблема в том, как сформулировать ученикам задачу и организовать ее решение. Рассмотрим возможные варианты.

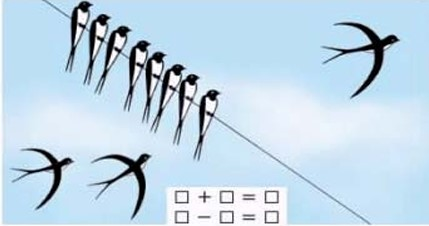
Рис. 1. Сюжетная картина для задачи на моделирование действий увеличения и уменьшения количества

Учитель говорит:

«На рисунке изображены сидящие и летящие ласточки. Внизу две математические модели, показывающие возможность увеличения или уменьшения количества сидящих ласточек. Рассмотрим первую модель. Пусть в первой клеточке будет поставлено число 8, отражающее количество ласточек, сидящих на проводе. Посмотрите, в левом нижнем углу изображены еще две летящие ласточки! Проанализируйте картинку и решите, какое число надо поставить во вторую клеточку!»

Кто-то из учеников откликается:

«Надо поставить 2, так как две ласточки сейчас прилетят и сядут на провод. Тогда получится: 8 + 2 = 10».

Учитель вновь обращается к классу:

«Это возможно, если считать, что две летящие ласточки сядут на проволоку.

Все с этим согласны?»

Но другой ученик может сказать:

«А вдруг эти ласточки летят мимо!»

Учитель спрашивает у класса: «Как быть тогда?».

Здесь может развернуться жаркая дискуссия. Окажется, что возможен даже такой вариант: «8» + «... » = «8».

Вот тут уже можно обсудить с детьми, как соотносится объект и его модель, что сначала надо решить, что мы отображаем в модели. Создаются предпосылки для достижения такого метапредметного образовательного результата, как «освоение начальных форм познавательной рефлексии».

Далее можно обсуждать, что означает пустая клеточка. Это уже подход к такому мета- предметному результату, как «овладение базовыми предметными и межпредметными понятиями, отражающими существенные связи и отношения между объектами и процессами». Число «ноль» вводить еще рано, но предпосылки для этого создаются.

Потом можно такое же обсуждение провести со второй моделью:

«. » — «. » = «. ».

В этом случае надо рассмотреть варианты интерпретации направления полета ласточки, изображенной в правом верхнем углу.

В качестве второго примера рассмотрим другую задачу, представленную на рис. 2 [7, с. 52]. Ученикам нужно определить, какой из арифметических примеров можно считать математической моделью для смысла сюжетной картинки.

Рис. 2. Сюжетная картина для задачи на моделирование действий, связанных с определением остатка   

Множественность решений задачи, изображенной на рис. 2, определяется, по крайней мере, двумя обстоятельствами.

Во-первых, она связана с неопределенностью значения наполовину окрашенной доски забора. Ее следует считать окрашенной или неокрашенной? В зависимости от решения этого вопроса выбор соответствующего арифметического примера будет разным. Это создает основу для такого метапредмет- ного результата, как «овладение логическими действиями классификации по родови­довым признакам, установление аналогий и причинно-следственных связей». Обсуждение можно построить по аналогии с предыдущим примером.

Предположим, что мы договорились, что эта доска считается окрашенной.

Тогда нужно, во-вторых, договориться, как мы интерпретируем цель действия юного маляра. То есть надо сформулировать задачу. Возможны следующие варианты.

Первый: «Мальчик покрасил 8 досок. Если он покрасит еще одну, сколько всего он покрасит досок?»

Второй: «Мальчик красил забор. В заборе было 9 досок. Ему осталось покрасить одну доску. Сколько досок он уже покрасил?».

В этом коллективном обсуждении создаются предпосылки для появления такого ме- тапредметного образовательного результата учащихся, как «умение анализировать условия адекватности отображения свойства объекта в его модели».

Но можно пойти дальше и задать детям вопрос: «А что если считать доску наполовину закрашенной? Что тогда будет?» Дробей дети еще не знают. Но они могут попробовать как-то трансформировать арифметические примеры. Вот тут разгорится интереснейшая дискуссия. А это уже есть предпосылка для «освоения способов решения проблем творческого и поискового характера».

Заключение

Такой тип работы учителя на уроке предполагает довольно высокий уровень культуры сценирования учебно-развивающих ситуаций. Мы отдаем себе отчет, что это возможно только в процессе серьезного обучения будущего учителя, прежде всего, в плане повышения уровня психологической подготовки. Это учтено в ФГОС ВПО психолого­педагогического образования [11].

Вместе с тем, назрела необходимость проведения специальных психолого-педагогических исследований методов сценирова- ния учебно-развивающих ситуаций. При этом необходимо учитывать логику развития ком­петенций будущих специалистов [1].