Введение
В современных условиях не всегда удаётся обеспечивать постоянный личный контакт преподавателей психологической диагностики со студентами с целью передачи необходимого неформального профессионального опыта. Это обусловлено тем, что аудиторные занятия ограничены по времени, а число студентов достаточно велико. Для повышения эффективности преподавания используются различные средства, которые не только дают знания о правилах применения каждой конкретной методики, но и навыки корректного проведения диагностических процедур, а также наблюдений за испытуемыми. В частности, с этой целью студентам демонстрируются соответствующие видеозаписи работы авторитетных специалистов с подробными комментариями. Иногда практикуется работа студентов в парах, когда они диагностируют своих товарищей. Однако эти приёмы не обеспечивают накопления достаточного практического опыта, и тестирование остаётся затянутой по времени и трудоёмкой процедурой.
Если практикующему специалисту для принятия решений требуется относительно короткий промежуток времени, за который он сможет дать всестороннюю оценку, то сотрудники с меньшим опытом, как правило, подходят к процессу достаточно формально. Они применяют заранее заготовленный набор методик, полностью проводят их в рекомендуемом порядке, что может занимать значительное время и утомить испытуемого, исказив полученный результат.
В подобных случаях полезны системы поддержки принятия решений [Психодиагностика в России, 2008], которые ускоряют процесс тестирования при использовании результатов математического моделирования. Это ускорение может быть связано, в частности, с анализом временнόй динамики прохождения каждого теста, косвенно отражающей уровень способностей. Подобный инструмент даёт практикующему специалисту дополнительную информацию для анализа и предоставляет рекомендации по выбору следующего теста, обладающего, по сравнению с прочими, наибольшей для данного испытуемого дифференцирующей способностью. Такие рекомендации, не являясь обязательными и не лишая специалиста возможности получения собственного опыта, направляют его по наиболее эффективному и надёжному пути. Следует отметить, что процесс тестирования при этом не становится полностью автоматическим в силу многокомпонентности процедуры оценки способностей и наличия дополнительных неформализуемых критериев.
Перспективность и актуальность данного подхода при обучении студентов-психологов обусловлена тем, что им при работе с психометрическими методиками часто недостает наблюдений, обязательных для накопления опыта клинического и личностного анализа, что приводит к значительным затратам финансовых, временных и других ресурсов, необходимых для получения полезной информации. Несмотря на то что интеллектуальные системы не дают навыков непосредственного общения с респондентом и соответствующего профессионального опыта, они позволяют в реальных условиях сосредоточиться на освоении важнейших особенностей практической работы с испытуемыми. К преимуществам этих систем относятся:
- удобство адаптации под любые методики;
- повышение доступности знаний, необходимых для специалиста;
- развитие навыков самостоятельной работы у студентов;
- повышение надёжности результатов тестирования;
- интенсификация процесса тестирования.
В основу математической концепции построения подобных систем и их программной реализации могут быть положены различные принципы организации и аппарат: определённые типы нейронных сетей [1; 2; 6; 10;17], экспертные системы [3; 4;12], обучаемые сети Маркова [7–9;11;16;18;19] и другие структуры. Однако сравнительный анализ показал, что перечисленные средства, за исключением марковских моделей и нейронных сетей, не обеспечивают должную универсальность и простоту адаптации к новым тестам, для каждого из которых фактически приходится разрабатывать отдельный специализированный программный продукт. С учетом развитых возможностей для вероятностного прогнозирования, отработанного аппарата идентификации [9;11;16;18] и простоты интерпретации полученных результатов, наиболее подходящим типом математических моделей для реализации поддержки принятия решений при проведении психологического тестирования, а также для организации психологического тренинга оказались марковские процессы с непрерывным временем.
В этой работе рассмотрена концепция системы поддержки принятия решений, предназначенной для использования в процессе психологического тестирования. Этот подход может быть использован при создании инструментальных средств, предназначенных для диагностики способностей и компетенций, а также организации и совершенствования процесса обучения.
Математические модели для представления динамики прохождения тестов
Под психологическим тестом далее понимается специально разработанный набор заданий, обеспечивающий оценку определённых способностей (например, способности к логическому мышлению или невербальный интеллект). Полагается, что ответы на вопросы заданий могут быть верными или неверными. Тесты, связанные с построением психологического профиля, и им подобные, в которых любой ответ является корректным, здесь не рассматриваются. Предполагается, что психологический тест позволяет разделить испытуемых на ряд категорий, соответствующих различным уровням исследуемого признака.
Динамика прохождения таких тестов определённым образом связана с категориями, к которым относятся испытуемые. Человек, дающий быстрые и правильные ответы на предъявляемые задания, как правило, обладает высоким уровнем оцениваемой способности. В свою очередь, долгие размышления над заданиями, как правило, свидетельствуют о неуверенности в ответах и, следовательно, об относительно более низком уровне способностей.
Модели для описания динамики переходов от одного задания к другому могут быть представлены ориентированными графами, вершины которых соответствуют состояниям (текущим заданиям), а дуги – переходам.
В случае моделей с непрерывным временем процесс тестирования может рассматриваться как случайное блуждание по графу с переходами из одного состояния в другое согласно направлениям дуг. Эти переходы мгновенны и происходят в случайные моменты времени.
Предполагается, что для них выполняются следующие два свойства пуассоновских потоков событий:
- ординарность (поток называется ординарным, если вероятность появления двух и более событий в течение малого интервала времени намного меньше, чем вероятность появления за это же время одного события);
- независимость приращений (это свойство означает, что количества событий, попадающих в два непересекающихся интервала, не зависят друг от друга).
Можно показать, что в рассматриваемых потоках число событий X , попадающих в любой временной интервал длины τ , начинающийся в момент t , распределено согласно закону Пуассона:
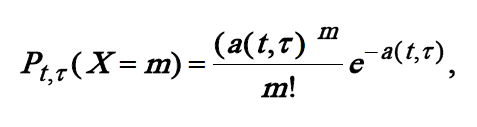
где Pt,τ (X=m) – вероятность появления m cобытий в течение рассматриваемого интервала, a(t,τ) – cреднее число событий, попадающих в интервал длины τ, начинающийся в момент времени t. Далее будут рассматриваться только стационарные потоки (в которых a(t,τ)= ητ, η=const). Параметр η называется интенсивностью стационарного потока. Он равен среднему числу событий в единицу времени. Средняя продолжительность времени между двумя смежными событиями в этом случае равна 1/η.
Упомянутые выше предположения о свойствах потоков событий обычны для прикладных задач, так как эти потоки (или потоки, близкие к ним по свойствам) часто встреча ются на практике благодаря предельным теоремам для потоков событий [13;15].
При указанных предположениях динамика изменения во времени вероятностей пребывания системы в различных состояниях описывается системой обыкновенных дифференциальных уравнений Колмогорова, в которой каждому состоянию соответствует уравнение
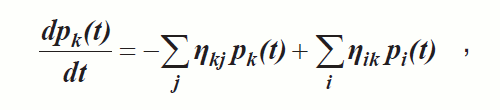
где k – индекс состояния; pk и pi– вероятности нахождения в k-м и i-м состояниях; ηki – интенсивности потоков, выходящих из состояния k; ηik – интенсивности потоков, входящих в состояние k. Для интегрирования указанной системы необходимо задать начальные условия: p0(0),p1(0),...,pn(0). Нормализующее условие 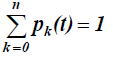 выполняется в любой момент времени.
выполняется в любой момент времени.
Для моделей с непрерывным временем неизвестными (свободными) параметрами модели являются интенсивности потоков событий. Их значения определяются путем сравнения наблюдаемых и прогнозируемых гистограмм, описывающих распределения частот пребывания в состояниях модели, а именно: вычисляются значения, обеспечивающие наилучшее соответствие наблюдаемых и ожидаемых частот попадания в определенное состояние системы в заданные моменты времени. Прогнозируемые вероятности нахождения в состояниях получаются путем численного интегрирования систем уравнений Колмогорова.
Марковские модели с непрерывным временем и свободными параметрами, которые идентифицируются по данным наблюдений, называются сетями Маркова [7; 8; 16–19]. Для описания, как при прохождении заданного теста вероятности нахождения в заданных состояниях изменяются со временем, применяются сети Маркова, представленные на рисунке. Предполагается, что тест состоит из определённого количества заданий, каждое из которых может быть выполнено правильно или не выполнено. Состояния Si,+ (i=1,…,m) соответствуют правильному выполнению i-го задания, а Si,- – его невыполнению или неправильному выполнению. S0 – начальное состояние, в котором испытуемый находится до выполнения теста. Интенсивности переходов между состояниями a, b, c, d, x, y, w и z идентифицируются отдельно для каждого уровня способностей по выборкам испытуемых, причём x, y, w и z отражают изменение способности выполнять задания теста со временем.
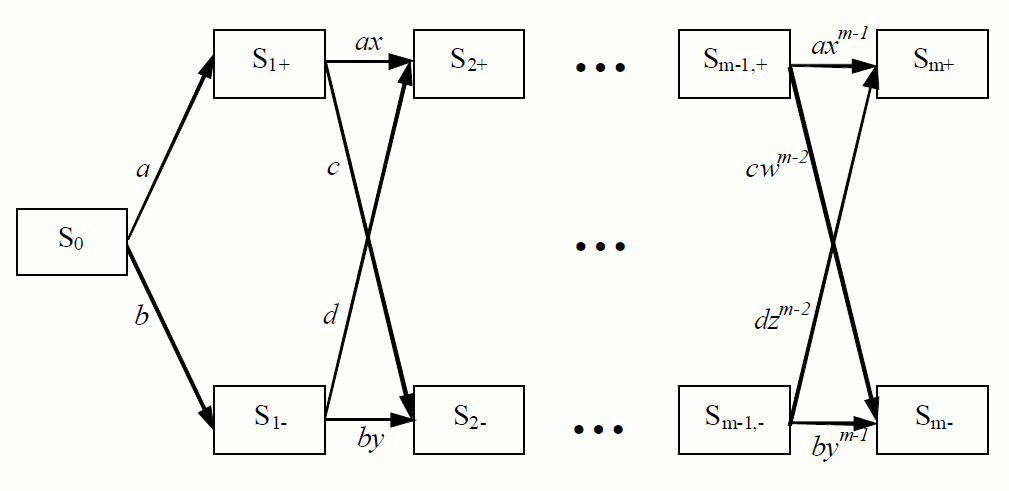
Рис. Сеть Маркова, представляющая процесс прохождения теста из m заданий
Динамика вероятностей нахождения в различных состояниях указанной сети описы- вается следующей системой обыкновенных дифференциальных уравнений:
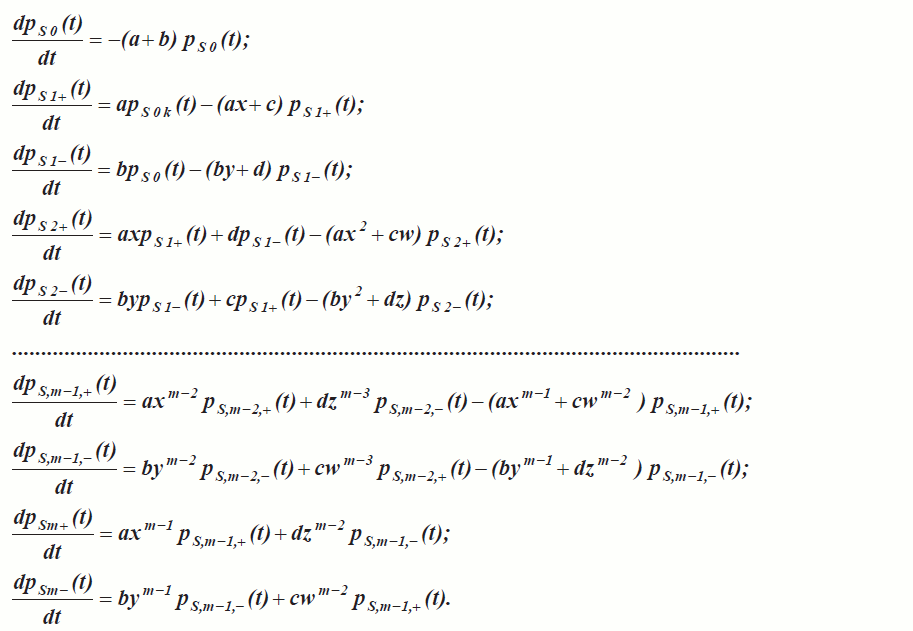
Здесь Ps*(t) есть вероятность нахождения в состоянии S* в момент времени t. В момент начала тестирования Psо(0)=1, а остальные вероятности пребывания в состояниях сети Маркова равны нулю.
Для упрощения задачи интенсивности потоков в ряде случаев могут полагаться зависящими друг от друга, включая тривиальный вариант: x=y=w=z, a=b, c=d. Оптимальный выбор подобных зависимостей опирается на технику проверки статистических гипотез.
Процедура оценки знаний или способностей
Процедура адаптивного тестирования заключается в последовательном предъявлении испытуемому тестов из заданного набора, которые не повторяются. Процедура измерения завершается по достижении заданного условия, накладываемого на вероятность наиболее правдоподобного варианта диагноза (например, можно потребовать, чтобы эта вероятность превышала 0,7). Если указанное условие не выполняется в течение всей процедуры тестирования, испытуемому предъявляется весь заготовленный набор тестов.
Психолог и испытуемый работают за разными компьютерами, между которыми организован обмен данными. Монитор испытуемого служит для предъявления тестов, а монитор психолога – для отображения результатов тестирования и информации, необходимой для выбора очередного теста. На мониторе первого после выбора теста вторым появляется соответствующее задание, которое он пытается выполнить, сидя за своим компьютером. Испытуемый не должен видеть данные, отображаемые на мониторе психолога.
После попытки выполнения каждого теста вычисляются:
- вероятности различных вариантов диагнозов при условиях принадлежности испытуемого к каждой из диагностируемых групп и нахождения в контрольный момент времени в наблюдаемом состоянии сети;
- вероятности различных вариантов диагнозов при условиях принадлежности испытуемого к каждой из диагностируемых групп и нахождения по истечении заданного фиксированного интервала времени в конечном состоянии Sm+ каждого из непредъявленных к данному моменту тестов.
Стратегия лица, принимающего решение о последовательности предъявления тестов, обусловлена необходимостью обеспечения за наименьшее время наибольшей дифференциации результата тестирования, представленной условием, накладываемым на вероятность наиболее правдоподобного варианта диагноза. Эта задача не имеет строго определённого решения вследствие известной неопределённости реальных действий испытуемого, включая непредсказуемое время выполнения заданий. Поэтому при отсутствии каких-либо дополнительных аргументов принимающему решение лицу следует, как правило, выбирать в качестве следующего такой тест, который приводит к наибольшей дифференциации самого вероятного диагноза от его остальных вариантов при условии нахождения испытуемого в соответствующем конечном состоянии Sm+ по истечении заранее фиксированного интервала времени. Такой подход обеспечивает близкую к оптимальной последовательность прохождения тестов и допускает различные вариации процедуры измерения в зависимости от опыта и дополнительной информации, которыми располагает психолог.
Расчет вероятностей диагнозов при выполнении очередного теста производится по формуле Байеса. Они рассчитываются для каждого из рассматриваемых вариантов диагноза в контрольный момент времени для наблюдаемого состояния сети, в котором испытуемый оказывается после выполнения последнего предложенного ему задания:
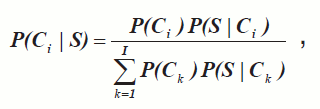
где Сi – событие, связанное с наличием у испытуемого i-го варианта диагноза (i=1,…,I), S – событие, связанное с нахождением в наблюдаемом состоянии сети в контрольный момент времени, P(Ci ) – априорная вероятность наличия у испытуемого i-го варианта диагноза, P(S|Ci ) – вероятность нахождения в наблюдаемом состоянии сети в контрольный момент времени при наличии i-го варианта диагноза, P(Ci |S) – вероятность i-го варианта диагноза при условии нахождения в наблюдаемом состоянии сети в контрольный момент времени. Вероятности P(S|Ci ) вычисляются путём численного интегрирования приведённых выше уравнений Колмогорова.
Вероятности нахождения по истечении заданного интервала времени в конечном состоянии Sm+ каждого из непредъявленных тестов рассчитываются для всех рассматриваемых вариантов диагноза по аналогичной формуле:
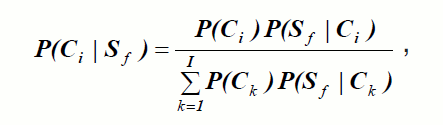
где Сi – событие, связанное с наличием у испытуемого i-го варианта диагноза (i=1,…,I), Sf – событие, связанное с нахождением в состоянии Sm+ по истечении заданного интервала времени, P(Ci ) – априорная вероятность наличия у испытуемого i-го варианта диагноза, P(Sf |Ci ) – вероятность нахождения в состоянии Sm+ по истечении заданного интервала времени при наличии i-го варианта диагноза, P(Ci |Sf ) – вероятность i-го варианта диагноза при условии нахождения в состоянии Sm+ по истечении заданного интервала времени. Вероятности P(Sf |Ci ), как и в предыдущем случае, вычисляются путём численного интегрирования уравнений Колмогорова. В качестве априорных вероятностей P(Ci ) в формулу следует подставлять вероятности P(Ci |S), вычисленные по результатам прохождения последнего выполненного теста.
Наиболее вероятным вариантом диагноза является тот, при котором достигается наибольшая условная вероятность , вычисленная по результатам прохождения последнего выполненного теста. Распределение вероятностей {P(Ci|S}i=1,...I позволяет оценить степень надёжности этой оценки.
Идентификация сетей Маркова
Вероятности P(S|Ci ), определённые в предыдущем разделе, могут быть вычислены путём численного интегрирования при наличии идентифицированных оценок свободных параметров a, b, c, d, x, y, w и z. Идентификации сетей Маркова проводятся по выборкам испытуемых для каждого из рассматриваемых вариантов диагноза отдельно. Каждому варианту диагноза Ci, i=1,…,I при этом ставится в соответствие свой уникальный набор оценок параметров модели, что позволяет в дальнейшем выявлять значение этого показателя, наилучшим образом согласующегося с наблюдениями. Таким образом, вероятности и интенсивности переходов являются функциями двух характеристик: варианта диагноза и трудности задачи. Число вариантов диагноза – это дискретный параметр, который задаёт разрешающую способность оценки данной характеристики и устанавливается при решении каждой прикладной задачи в зависимости от объёма выборки испытуемых, имеющейся у исследователя при решении задачи идентификации, и желаемой точности результата.
С каждой изменяющейся со временем гистограммой пребывания в состояниях модели связывается марковский процесс с дискретными состояниями. Статистика Пирсона:
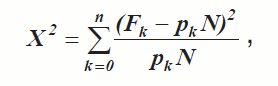
где N – число элементов в выборке, pk – прогнозируемая вероятность попадания в k-е состояние модели, а Fk – наблюдаемая частота нахождения в k-м состоянии модели, используется как мера соответствия в том смысле, что ее большие значения означают плохое согласование прогнозируемых и наблюдаемых результатов, а малые значения – хорошее согласование. Для идентификации модели минимизируется сумма указанных статистик в те моменты времени, для которых имеются результаты наблюдений. Наблюдаемые количества попаданий в различные интервалы трудностей задач определяются по результатам тестирования группы испытуемых. В качестве искомых оценок свободных параметров моделей используются значения, обеспечивающие наилучшее соответствие наблюдаемых и прогнозируемых частот попадания в определенное состояние системы в заданные моменты времени.
Доказано, что при выполнении ряда общих условий значения статистики Пирсона X 2, получаемые при подстановке истинных решений, асимптотически описываются распределением χ2 с n–l cтепенями свободы, где l – число определяемых параметров, причем вычисленные значения свободных параметров при увеличении объема выборки сходятся по вероятности к искомому решению [5, с. 462–470]. Это позволяет использовать приведенную статистику для проверки гипотезы, что полученный прогноз согласуется с результатами наблюдений. Данный способ идентификации свободных параметров называется методом минимума χ2 [Крамер, 1976] и даёт решения, близкие к полученным методом максимального правдоподобия [там же, с. 461–462].
В случае сетей Маркова используемая процедура вычисления оцениваемых параметров состоит из двух этапов. На подготовительном этапе с помощью электронной таблицы для указанной системы дифференциальных уравнений кодируется численная схема интегрирования, позволяющая вычислять вероятностные функции pk [Куравский, 2005; Куравский, 2010; Kuravsky, 2003; 18]. Эти функции вычисляются с некоторым заданным временным шагом. Для вычисления решения с приемлемой точностью оказались достаточными методы Рунге-Кутта или их эквиваленты.
На заключительном этапе запускается численная процедура многомерной нелинейной оптимизации 3 [Куравский, 2005; Куравский, 2010; Kuravsky, 2003; 18], позволяющая получать искомые значения свободных параметров. Полученные оценки свободных параметров рассматриваются как характеристики модели, выявленные в результате наблюдений. Рассмотренный критерий также позволяет сравнивать между собой различные варианты марковских моделей, выбирая среди них оптимальные [Куравский, 2002; Куравский, 2010; 19].
Основные результаты и выводы
Разработана концепция системы поддержки принятия решений, предназначенной для использования в процессе психологического тестирования и основанной на использовании марковских моделей с дискретными состояниями и непрерывным временем.
Стратегия лица, принимающего решение о последовательности предъявления тестов, обусловлена необходимостью обеспечения за наименьшее время наибольшей дифференциации результатов тестирования, представленной условием, накладываемым на вероятность наиболее правдоподобного варианта диагноза.
Решение о выборе последующего теста принимается на основе следующей информации, предъявляемой после попытки выполнения каждого теста и получаемой с помощью байесовских оценок:
- вероятности различных вариантов диагнозов при условиях принадлежности испытуемого к каждой из диагностируемых групп и нахождения в контрольный момент времени в наблюдаемом состоянии сети;
- вероятности различных вариантов диагнозов при условиях принадлежности испытуемого к каждой из диагностируемых групп и нахождения по истечении заданного фиксированного интервала времени в конечном состоянии каждого из непредъявленных к данному моменту тестов.
Разработаны методы идентификации параметров сетей Маркова, основанные на применении метода минимума χ2 и численной процедуры многомерной нелинейной оптимизации.
Представленная концепция может быть использована при создании инструментальных средств, предназначенных для диагностики способностей и компетенций, а также организации и совершенствования процесса обучения.