Концепция системы поддержки принятия решений при тестировании интеллекта

Введение

Тесты, предназначенные для измерения уровня интеллектуального развития, являются наиболее распространенными в психодиагностике. Проявления интеллекта многообразны, но им присуще то общее, что позволяет отличить их от других особенностей поведения, а именно: вовлечение в любой интеллектуальный акт мышления, памяти, воображения, всех психических функций, которые обеспечивают познание окружающего мира. Это нашло свое отражение в многочисленных тестах для оценки различных интеллектуальных функций (тесты логического мышления, смысловой и ассоциативной памяти, арифметические, пространственной визуализации и т. д.). В настоящее время проблема большого числа заданий в данных методиках является актуальной, так как требует больших временных затрат, достаточно длительной концентрации внимания и собранности от испытуемого. Это является основанием для разработки системы поддержки принятия решений (СППР) при тестировании, которая позволила бы сократить число выполняемых заданий без потери точности итоговой оценки результатов, а также учитывала бы динамику прохождения тестирования. Исследования, проведенные в этой области, показали эффективность применения нейронных сетей и других обучаемых структур для решения данной задачи [Куравский, 2011].

В ходе тестирования на испытуемого оказывают влияние такие внешние факторы, как усталость, подсказки и др., что искажает конечный результат и приводит к появлению артефактов. Представляемая здесь система тестирования позволяет бороться с этими явлениями, устраняя их на основе сравнения наблюдаемых и прогнозируемых результатов ответов на вопросы для разных уровней способностей испытуемых. В качестве инструмента для сравнения используется фильтр Калма- на - нестационарная система с обратной связью, включающая в себя как составную часть формирующий фильтр, воспроизводящий идеализированную модель поведения [Куравский, 2012].

Для решения аналогичных задач также применяются марковские модели [Куравский, 2012а]. Преимуществом разрабатываемого подхода является отсутствие проблемы оценки сложности задачи. С помощью марковских моделей мы не в состоянии описать структуру интеллектуальных способностей - влияние факторов генетики и среды. Использование марковских моделей предпочтительно в задачах адаптивного тестирования, где мы сталкиваемся с проблемой изменения структуры и порядка предъявления тестовых вопросов. Разрабатываемый нами подход позволяет проанализировать динамику прохождения тестовых заданий для различных уровней развития способностей испытуемых.

Модель процесса тестирования

В проведенном ранее исследовании [Панфилова, 2011] описан процесс исследования факторных моделей интеллекта, разработанных согласно двум центральным теориям, описывающим структуру интеллектуальных способностей. Обе модели показали свою адекватность наблюдаемым параметрам при исследовании влияния генетики и среды на интеллектуальные способности. Гнездовая факторная модель интеллекта [Neale, 1992], согласно которой было разработано большое число тестов интеллекта, показана на рисунках 1 и 2 в виде симплекс-структуры [Boomsma, 1987], представляющей процесс тестирования.

Структура модели учитывает влияние факторов генетики и среды на наблюдаемые параметры. Результаты ответов испытуемых представлены наблюдаемыми параметрами T (см. рис. 1). При верном ответе на вопрос тестовой методики параметр T принимает значение расчетной сложности вопроса, а при неверном - приравнивается к нулю. Также применяется аналогичная факторная модель (см. рис. 2), где в качестве наблюдаемых параметров L используется время, затраченное испытуемыми при ответе на соответствующие вопросы теста.

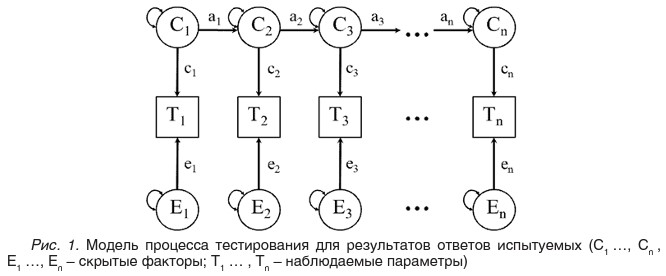
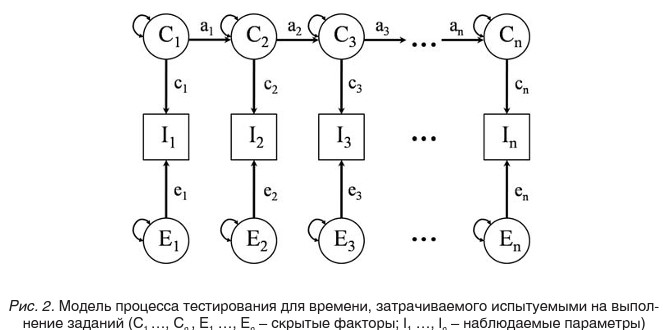
Для демонстрации работы системы используется тест «Продвинутые прогрессивные матрицы Равена» [Равен, 1998] из 36 вопросов, ди­агностирующих уровень развития общего интеллекта. После тестирования испытуемых определенной возрастной группы получаются наборы T¡, которые являются результатами ответов на вопросы, а также наборы I¡, отражающие время, затраченное испытуемыми при ответе на каждый вопрос. Наблюдаемые параметры T¡ в случае верного ответа представляют сложность тестового вопроса, выраженную в логитах. Логит уровня трудности задания - это единица измерения сложности тестового вопроса, введенная Г. Рашем и вычисляемая как натуральный логарифм отношения доли неправильных ответов на задание теста к доле правильных ответов на тот же вопрос по множеству испытуемых [Rasch G .Probabilistic]. Данные о проценте верных ответов на каждый вопрос теста для большой выборки испытуемых были предоставлены разработчиками теста. Наборы наблюдаемых параметров, переведенных в логиты, могут быть разделены по итоговому результату на несколько групп сложности.

Идентификация параметров модели

Элементы прогнозируемой ковариационной матрицы представляют собой аналитические выражения относительно свободных параметров модели. Дисперсия C¡ фактора выражается формулой:

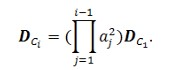
Оценки свободных параметров модели определяются как компоненты псевдореше­ния переопределенной системы уравнений [Куpавский, 2011]:

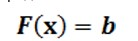
где F(x) - n-мерный нелинейный оператор, действующий на m-мерный вектор x свободных параметров модели, компоненты которого являются аналитическими выражениями прогнозируемых дисперсий и ковариаций наблюдаемых переменных через m свободных параметров рассматриваемой факторной модели; b - вектор-столбец, составленный из n выборочных оценок дисперсий и ковариа­ций наблюдаемых переменных.

Для вычисления псевдорешения может применяться любой подходящий численный метод нелинейной многомерной локальной оптимизации, в котором критерий минимизации представлен евклидовой нормой невязки. В частности, для этого приемлемы градиентные методы.

Идентификация свободных параметров модели проводится для каждого уровня развития способностей как для модели результатов ответов испытуемых, так и для модели времени, затраченного при ответе на каждый вопрос теста, по выборочным ковариационным матрицам с использованием метода наименьших квадратов. После получения значений факторных нагрузок, используя метод Монте-Карло, имеется возможность путем генерации нормально распределенных случайных значений фактора C1 с различными стандартными отклонениями, лежащими в окрестности идентифицируемого стандартного отклонения C1, и долями случайных компонентов, выходящими за рамки доверительных интервалов, используя выражения наблюдаемых переменных T и Ii через факторы модели, получить выборки наблюдаемых значений для каждой из групп различного уровня способностей с учетом вариативности, присутствующей в генеральной совокупности.

Оценка адекватности модели

Выборка полученных значений наблюдаемых параметров используется для обучения самоорганизующихся карт признаков (карт Кохонена) [Кохонен, 2008] подходящей размерности с целью получения выборок евклидовых расстояний между входным вектором, описывающим процесс прохождения тестирования испытуемым, и центрами нейронов-победителей обученной сети. Учитывая достаточно высокую размерность входных векторов, характерную для практических задач, можно говорить о том, что распределение полученных евклидовых расстояний близко к нормальному. Выборочные оценки средних и дисперсий этих расстояний идентифицируют указанное распределение и позволяют оценивать вероятности превышения расстояния между полученным вектором ответов испытуемого, а также времени, затраченного при ответе на каждый вопрос, и соответствующим центром нейрона-победителя, что дае т возможность судить о степени адекватности модели наблюдениям.

Сопоставление рассмотренных выше вероятностных мер адекватности моделей для различных стандартных отклонений и средних процентов компонентов, выходящих за границы доверительных интервалов, позволяет выявлять наиболее правдоподобные сочетания достигнутой точности идентификации, представляемой оценкой стандартного отклонения, и структуры значимых погрешностей в определении компонентов полученного псевдорешения. Геометрическая иллюстрация, поясняющая суть процедуры в случае нелинейного оператора F(x), приведена на рис. 3.

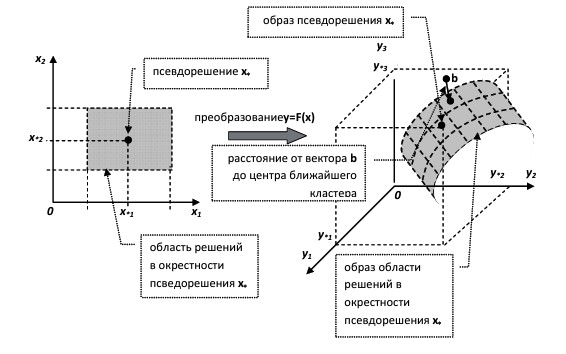
Рис. 3. Геометрическая интерпретация нелинейного преобразования области допустимых решений

Предлагаемый подход позволяет исследовать значимость различий между наиболее правдоподобными вариантами факторных моделей, используя технику проверки статистических гипотез. Свободные параметры этих моделей предварительно идентифицируются с помощью рассмотренного выше метода. Сравнение опирается на сопоставление отношений r = a/m, где о есть наиболее правдоподобное стандартное отклонение сгенери­рованных нормально распределенных значений свободного параметра модели, а m - соответствующее среднее значение распределения. Отношение r при генерации выборок поддерживается равным для всех параметров одной модели, но может различаться для разных моделей, которые в общем случае могут иметь и разные средние процентные соотношения компонентов, лежащих вне доверительных интервалов.

Пусть указанные отношения для сравниваемых моделей равны, соответственно, r1=a/m, и r2 = о2/т2, причем r1 < r2. Сравнение моделей выполняется при одном и том же относительном стандартном отклонении ax=r1=r2m2, когда среднее значение m1 выбирается в качестве единицы измерения (приравнивается к 1), и опирается на оценку вероятности получения приведенного среднего m2=r1/r2, а именно: для случайной величины X вычисляется вероятность P(m2<X<1) = &(1)-&(m2) пребывания в интервале [m2;m1 = 1], где Ф есть функция нормального распределения со средним значением 1 и стандартным отклонением о*. Если эта вероятность превышает заданный критический уровень, который обычно принимается равным 0,05, различие между моделями рассматривается как статистически значимое, в противном случае - как незначимое [Куpавский, 2011].

Оценивая степень адекватности модели после ответа испытуемым на каждый вопрос теста, можно судить, к какому уровню развития способностей он ближе по результатам и по времени, затраченному при ответе на каждый вопрос. Когда степень соответствия какому-либо из уровней достигнет необходимого уровня значимости, процесс тестирования завершается и делается вывод, какому уровню развития способностей в наибольшей степени соответствует данный испытуемый.

Устранение артефактов тестирования

Для устранения артефактов тестирования используется многомерный цифровой фильтр Калмана. Его выбор среди близких по содержанию подходов является оптимальным, поскольку он наилучшим образом согласуется с принятой концепцией тестирования и контекстом ее использования. В частности, этот фильтр [Куравский, 2012]:

•     в отличие от фильтра Винера способен обрабатывать текущую информацию об ответах испытуемого в реальном времени, формируя свои оценки сразу же после получения очередного ответа и не требуя полного протокола тестирования, который недоступен до завершения всей процедуры ответов на вопросы;

•     в отличие от фильтра Стратоновича использует только линейные методы оценки, наилучшим образом согласующиеся с применяемой линейной дифференциальной моделью адаптивного тестирования, и не приводит к неоправданному усложнению процесса решения;

•     в отличие от фильтра Льюинбергера учитывает ошибки наблюдений и обеспечивает оптимальные оценки.

В случае данного варианта процесса тестирования наблюдаемый процесс представляет историю ответов испытуемого на вопросы из субтеста. Он выражается вектором

у которого с каждым новым ответом на вопрос размерность увеличивается на 1 при ограничении из k вопросов субтеста, где n - дискретный момент времени. В свою очередь, исследуемый информационный процесс, отражающий динамику изменения влияния генетического фактора на возможность испытуемого ответить на предъявляемый вопрос, представлен вектором

размерность которого определяется числом вопросов в методике, а количество компонентов увеличивается на 1 при ответе на очередной вопрос. Полагается, что

Х[Айзенк, 1994] = 1.

Уравнения информационного и наблюдаемого процессов, используемые при построении многомерного цифрового фильтра Калмана для моделей рассматриваемого типа 1, имеют вид [Шахтарин, 2010]

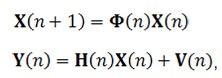
где оценка характеристик случайных ошибок наблюдений проводится при идентификации модели и представляется вектором

на который накладываются следующие условия: E(V[«])=0, E(V[w]VT[¿])=R[«]ó[«-¿], E(X[0] VT[¿])=0, где R — симметричная положительно определе нная матрица, которая полагается не зависящей от времени. При проведении практических расчетов эта матрица заменятся на одну из своих выборочных оценок R, полученных для каждого из рассматриваемых уровней способностей на основе результатов наблюдений. Матрица формирующего фильтра Ф размерности (k+1) х (k+1) содержит коэффициенты переходов между факторами C_k:

Эти коэффициенты определяются идентификации модели. Диагональная трица наблюдений Н содержит генетические факторные нагрузки, оказывающие влияние на наблюдаемые параметры:

X(n + 1) = Ф(п)Х(п) + К(п + 1) [Y(n + 1) - -Н(п+1)Ф(п)Х(п)],

где K (п = 1) - матричный коэффициент усиления фильтра Калмана.

Данный коэффициент вычисляется по формуле

К(п+ 1) = Р(п + 1)Нт(п+ 1)[Я(п+ i);

Р(п + 1)Яг(п + 1) + Л(п + I)]-1 где Р(п + 1) - априорная матрица дисперсий, определяемая следующим уравнением:

Р(п +1) = Ф(п)Р(п)Фт(п) + Г(п)9(п)Гт(п)

В этом уравнении Р(Т1 + 1) - апостериорная матрица дисперсий, представленная следующим уравнением:

Р(п+1)= [/-К(п+1)Я(п+1)]Р(п+1),

Начальное условие определяется эмпири- ческойоценкой дисперсии ошибки Р(1) = с при п = 1, которая полагается одинаковой для всех типов моделей.

Фильтрация Калмана выполняется автономно для каждого из уровней способностей, учитываемых при постановке решаемой задачи.

Особенности использования
представленной системы с различными тестами интеллекта

Существует большое число тестов интеллекта, измеряющих одну или несколько различных способностей. Рассмотренный тест «Продвинутые прогрессивные матрицы Равена» состоит из одного субтеста. Популярный тест Айзенка [Айзенк, 1994] включает суб­тесты, измеряющие вербальные и образные способности, абстрактное мышление и т. д. Тест Амтхауэра [Елисеев, 2003] включает диагностику вербального, счетно-математического, пространственного, мнестического компонентов интеллекта.

Представленная СППР может использоваться как при работе с вышеперечисленными, так и с самыми разнообразными тестами интеллекта, поскольку предполагает работу не со всей методикой в целом, а с составляющими ее субтестами. В момент, когда система с заданной точностью может отнести испытуемого к какому-либо уровню развития определенной способности, тестирование по данному субтесту прекращается. Таким образом, возможно значительное сокращение числа вопросов в методиках, включающих множество субтестов, при сохранении порядка предъявления вопросов, что имеет важное значение для стандартизации тестов.

Существует ряд методик, которые невозможно использовать в рамках представленной системы. К ним, например, относится тест Векслера [Дружинин, 1999], который требует обязательного присутствия психолога, проводящего исследование и принимающего активное участие в процедуре оценки.

Спектр применения СППР при тестировании интеллекта достаточно широк, поскольку для этого может использоваться любой тест, допускающий возможность создания его компьютерной версии.

Процесс настройки системы для использования новой тестовой методики включает в себя этапы:

•     уточнение размерности факторной модели процесса тестирования по каждому субте­сту;

•     проведение тестирования на выборке испытуемых для получения наборов ответов и временных показателей;

•     идентификацию факторных моделей для каждого уровня развития способностей;

•      генерацию нормально распределенной выборки случайных значений в окрестности Дисперсии фактора C1 с целью получения наборов значений Ti и Ii большой размерности, используемых при обучении самоорганизующихся карт Кохонена для каждого из рассматриваемых уровней развития способностей.

Основные результаты и выводы

1.   Разработана концепция новой системы поддержки принятия решений при тестировании интеллекта, основанная на использовании факторных моделей и позволяющая оптимизировать процедуру тестирования за счет сокращения избыточных заданий.

2.   Предложенный подход имеет преимущества по сравнению с использованными ранее способами тестирования, что обусловлено его большей информативностью, связанной с уче том влияния фактора времени на результаты тестирования, а также уменьшением времени прохождения процедуры испытаний.

3.   Устранение искажающих оценки артефактов, обусловленных воздействием на испытуемого факторов внешней среды, выполняется на основе сравнения наблюдаемых и прогнозируемых результатов прохождения теста при разных уровнях способностей с помощью многомерного цифрового фильтра Калмана, приспособленного для решения задачи тестирования.

Благодарности

Автор выражает благодарность доктору психологических наук, члену-корреспонденту РАН, заведующему лабораторией психологии и психофизиологии творчества Института психологии РАН профессору Дмитрию Викторовичу Ушакову, а также доктору технических наук, декану факультета информационных технологий МГППУ профессору Л. С. Куравскому за консультации и обсуждение результатов работы.