О повышении практической направленности теоретической подготовки учителей начальных классов в программах бакалавриата по направлению подготовки «Психолого-педагогическое образование»

Введение

В 2014-2015 гг. был осуществлен проект «Усиление практической направленности подготовки будущих педагогов в программах бакалавриата в рамках укрупненной группы специальностей «Образование и педагогика» по направлению подготовки «Психолого­педагогическое образование» (Учитель начальных классов) на основе организации сетевого взаимодействия образовательных организаций, реализующих программы высшего образования и начального общего образования» [6; 10; 12; 13].

Над совершенствованием методологических и педагогических подходов подготовки будущих педагогов посредством усиления практической направленности подготовки в программах бакалавриата трудились коллективы следующих вузов Российской Федерации:

•           ФГБОУ ВО «Московский государственный психолого-педагогический университет»;

•           ФГБОУ ВПО «Набережночелнинский институт социально-педагогических технологий и ресурсов»;

•           ФГБОУ ВПО «Омский государственный педагогический университет»;

•           ГБОУ ВПО «Ставропольский государственный педагогический институт»;

•           ФГБОУ ВПО «Чеченский государственный педагогический институт»;

•           ФГБОУ ВПО «Тюменский государственный университет»;

•           ФГБОУ ВПО «Сыктывкарский государственный университет».

Опыт данной работы показал, что возможно усиление практической направленности подготовки будущих педагогов в программах бакалавриата в рамках укрупненной группы специальностей «Образование и педагогика» по направлению подготовки «Психолого­педагогическое образование» (Учитель начальных классов) на основе организации сетевого взаимодействия образовательных организаций, реализующих программы высшего образования и начального общего образования. У студентов развивается интерес к педагогической деятельности, формируется мотивация к овладению профессиональными компетенциями. Открывается перспектива развития педагогического образования на основе модульной образовательной программы [14; 20].

В процессе обсуждения с представителями оператора проекта и коллегами по апробации новых модулей на Всероссийской конференции по обсуждению результатов проектов модернизации педагогического образования (Москва, 18-20 ноября 2015 г.) определились возможные ресурсы усиления практической направленности подготовки будущих педагогов в программах бакалавриата в рамках укрупненной группы специальностей «Образование и педагогика» [2]. В соответствии с этим в проект ФГОС ВО 4 по укрупненной группе специальностей «Образование и педагогика» по направлению подготовки «Психолого­педагогическое образование» (Учитель начальных классов) было предложено добавить следующее:

1.         Увеличить общий объем практики до 90-100 зачетных единиц.

2.         Предусмотреть, чтобы в каждом модуле не менее 50% объема теоретических разделов было отведено на практикумы и практико-ориентированные темы, развивающие способность к анализу, рефлексии и планированию способов реализации фундаментальных положений психологии и педагогики в содержании начального образования и совершенствованию образовательных отношений (профессиональные пробы в форме анализа видеозаписей фрагментов уроков, анализа результатов диагностики образовательных результатов, проигрывание сценариев уроков и иных образовательных событий, освоение трудовых действий в каких-либо модельных формах или ситуациях, в том числе с использованием электронных симулято­ров уроков).

Проблема. В ходе дискуссий наибольшее количество вопросов вызвало второе предложение. В данном случае это было связано с широко распространенным мифом о том, что якобы усиление практической направленности подготовки будущих педагогов может привести к потере фундаментальности педагогического образования.

В качестве гипотезы можем высказать предположение о том, что этот миф связан с невниманием широкой педагогической общественности к теории и практике развивающего обучения. Давно не переиздавался один из выдающихся трудов в данном направлении - монография В.В. Давыдо­ва «Теория развивающего обучения», опубликованная еще в 1996 г. [8]. В этой книге показано, как фундаментальные положения психологии, педагогики, естественных и гуманитарных наук могут реализовываться в содержании и методах начального общего образования. Эти положения реализованы программах и учебно-методических комплектах дидактической системы В.В. Давы­дова и Д.Б. Эльконина для начальной школы, и сегодня существует достаточно большой объем методической литературы по данной теме.

Развивающее обучение занимает небольшую часть всей практики современной начальной школы. Вместе с тем в ряде современных учебно-методических комплектов идеи развивающего обучения вошли в содержание обучения младших школьников, но соответствующих авторитетных научно-методических трудов, где показано, как фундаментальные достижения наук и культуры воплотились в реалиях начального общего образования, мало. Такое же положение сложилось для методического обеспечения образования будущих учителей начальной школы: в основном создаются и издаются труды по методике преподавания конкретных дисциплин.

Опыт С.П. Саниной и М.В. Енжевской, участвовавших в нашем проекте, показал, что в рамках модуля «Введение в профессию уже на 1-м курсе студенты-бакалавры могут анализировать способы реализации фундаментальных знаний о природе в содержании таких учебных дисциплины для младших школьников, как «Окружающий мир» [20]. По нашему замыслу этот модуль должна была поддерживать дисциплина «Естественно-научная картина мира», где у студентов формируются универсальные компетенции, обеспечивающие понимание фундаментальных основ детских представлений о мире. Но мы столкнулись с тем, что в отечественной научно­методической литературе соответствующих работ нет. Поэтому для повышения практической направленности теоретической подготовки будущих учителей начальной школы актуально создание системы заданий для практикумов, развивающих способность студентов к анализу, рефлексии и планированию способов реализации фундаментальных положений естественных и гуманитарных наук всодержании начального общего образования.

Методические предложения для решения проблемы усиления практической направленности теоретического обучения студентов бакалавриата. Такую возможность мы видим в постановке студентам задач по обнаружению метапредметно- го содержания учебной деятельности младших школьников. С одной стороны, очевидна практическая направленность этих заданий, так как достижение метапредметных образовательных результатов является одним из требований ФГОС общего начального образования [3; 4; 17; 21; 22]. С другой - мы оказываемся в ситуации, аналогичной той, которая возникает в процессе решения так называемой учебной задачи в развивающем обучении, а именно необходимости выявления общих законов, определяющих данную предметную область, в чистом виде [5; 7; 9; 15; 19].

Пример 1. В дисциплине «Естественнонаучная картина мира» большой раздел посвящен принципам симметрии в живой и неживой природе, а также в искусстве. Перевести общие знания в этой области в практику можно через анализ диагностического задания для выпускников начальной школы.

Задание студентам на самостоятельную работу: «Проанализируйте предложенные диагностические задачи для младших школьников. Определите, какой принцип симметрии использован в каждой задаче. Можете использовать книгу: Шубни­ков А.В., Копцик В.А. Симметрия в науке и искусстве. М.: Наука. 1972, и другие пособия [1; 23].

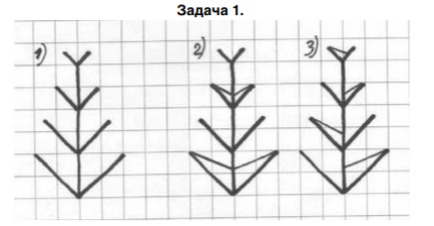
На рисунке 1 пункт 1 изображена схема узора.

Надо было к схеме добавить четыре прямых отрезка любой длины по одному определенному принципу так, чтобы сохранилась вертикальность узора.

Наташа предложила два варианта (см. Рис. 1, пункт 2 и 3). Выдержан или нет в каждом из рисунков один принцип для положения дополнительного отрезка? Выбери правильный ответ:

A)        Принцип выдержан в каждом рисунке (см. Рис. 1, пункт 2 и пункт 3).

Б) Принцип выдержан только в рисунке пункт 2.

B)        Принцип выдержан только в рисунке пункт 3.

Г) Принцип не выдержан ни в одном рисунке,

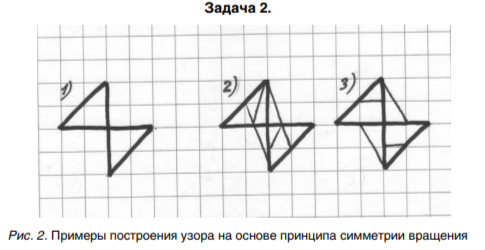
На рисунке 2 пункт 1 изображена схема узора. Если его повернуть вокруг центральной точки в пол-оборота, то узор совместится сам с собой.

Надо было к схеме добавить четыре прямых отрезка любой длины так, чтобы сохранилось вращательное свойство узора. Миша предложил два варианта (см. Рис. 2, пункт 2 и пункт 3). Выдержан или нет в каждом из рисунков один принцип вращательного узора?

Выбери правильный ответ:

A)         Принцип выдержан в каждом рисунке (см. Рис. 2, пункт 2 и пункт 3).

Б) Принцип выдержан только в рисунке пункт 2.

B)         Принцип выдержан только в рисунке пункт 3.

Г) Принцип не выдержан ни в одном рисунке.

(Правильным является ответ В.)

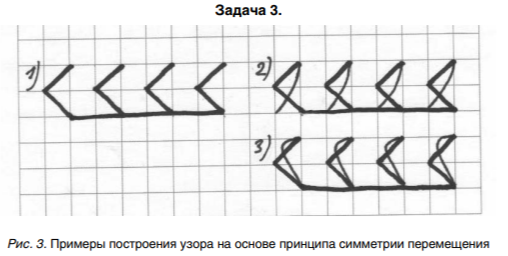
На рисунке 3 пункт 1 изображена схема узора.

Надо было к схеме добавить четыре изогнутых отрезка любой длины по одному определенному принципу так, чтобы сохранилась горизонтальность узора.

Таня предложила два варианта на (см. Рис. 3, пункт 2 и пункт 3). Выдержан или нет в каждом из рисунков один принцип для положения дополнительного отрезка?

A)         Принцип выдержан в каждом рисунке (см. Рис. 3, пункт 2 и пункт 3).

Б) Принцип выдержан только в рисунке пункт 2.

B)         Принцип не выдержан ни в одном рисунке.

Г) Принцип выдержан только в рисунке пункт 3.

(Правильным является ответ Г.)

На аудиторном занятии проводится обсуждение домашней работы. Студенты должны прийти к выводу, что в задаче 1 использована зеркальная симметрия, в задаче 1 - смметрия вращения, в задаче 3 - симметрия перемещения.

Следующие вопросы для коллективного обсуждения: «Могут ли эти задачи использоваться для диагностики метапредметных ком­петенций обучающихся? Каких именно? Для какого класса начальной школы?» 

После обсуждения предлагаются данные экспериментальной проверки диагностических задач. После дискуссии сообщается, что задачи проходили экспериментальную проверку в числе других диагностических заданий на контингенте выпускников начальных классов школ Центрального административного округа Москвы.

В таблице 1 представлены данные по результатам выполнения всех трех выше описанных задач.

Таблица 1

Распределение всех испытуемых по количеству успешно выполненных задач

Данные эксперимента показывают, что часть выпускников начальной школы вполне могут решать задачи, основанные на действиях сравнения и анализа способов построения симметричных фигур. В принципе, эти действия (воображаемое зеркальное отображение, вращение, горизонтальное перемещение) необходимы для анализа различных учебных схем и моделей. Но, видимо, опыта в решении таких задач достаточно не у всех младших школьников.

На гистограмме (см. рис. 4) видно, что распределение испытуемых по количеству решенных задач оказалось близким к нормальному. Следовательно, задачи такого типа можно использовать в пакете диагностических заданий для оценки метапредметных компетенций выпускников начальной школы

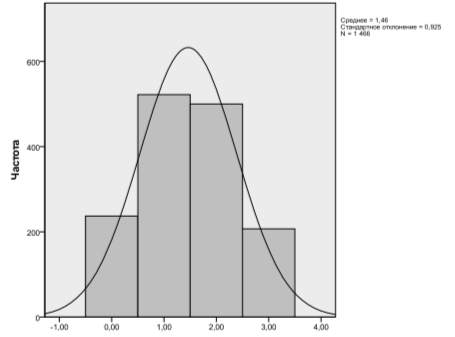
Рис. 4. Соответствие частот выполнения задач нормальному распределению

Предполагаемые выводы в конце группового обсуждения

Можно полагать, что задачи с использованием принципов симметрии вполне подходят для использования их в пакете методик диагностики метапредметных компетенций выпускников начальной школы. Дети этого возраста уже имеют элементарные представления о конструировании объектов на основе принципов симметрии. Удобство рассмотренных задач заключается в том, что на каждый принцип симметрии можно придумать много вариантов задач, не изменяя существенно их трудность. Это позволяет создавать компьютерные варианты методик для дистанционной диагностики образовательных результатов обучающихся.

Данное задание удобно еще и по той причине, что позволяет активизировать знания студентов по математической статистике.

Примеры 2. В рамках дисциплины «Естественно-научная картина мира» большое внимание уделяется методу анализа явлений на основе теоретико-множественных представлений. В частности, постоянно рассматриваются следующие понятия:

-           существенные и несущественные признаки объектов;

-           целое и часть;

-           объект и его модель (отображение существенных признаков объекта в модели);

-           множество и элемент множества;

-           пустое множество;

-           отношения множеств (больше, меньше, равно);

-           равенство (тождественность) множеств, взаимно однозначное соответствие множеств;

-           сложение (объединение) множеств;

-           вычитание (удаление части) множеств;

-           пересечение множеств;

-           количество элементов множества;

-           принадлежность элемента множеству.

На этих понятиях построена интерпретация большинства диаграмм.

Эти же понятия фактически присутствуют в современных учебниках математики для начальной школы, во многих задачах на моделирование ситуаций в сюжетных рисунках. По сути дела, большинство используемых моделей носит теоретико-множественный характер. А сами задачи формулируются как задания на выполнение следующих действий:

-           действия по установлению существенных и несущественных признаков объектов;

-           действия по определению целого и его части;

-           действия моделирования (отображение существенных признаков объекта в некоторой модели);

-действия по установлению соответствия объекта и его модели;

-           действия по сравнению множеств;

-           действия по установлению тождественности множеств;

-           действия сложения и вычитания множеств;

-           действия по определению количества элементов множества;

-           действия по определению принадлежности элемента множеству.

Поэтому будущим учителям надо понимать, какие понятия заложены в этих задачах.

Пример 2а.

Рассмотрим несколько задач из учебника математики для 1-го класса авторского коллектива Маро (см. рис. 5).

Возможны вопросы для коллективного обсуждения: «Какие задачи основаны на одних и тех же действиях с множествами? Какие задачи основаны на разных действиях с множествами? Какие признаки объектов являются существенными в задачах 5, 6, 7, а какие - несущественными? Есть существенная разница в моделях к задачам 5 и 6?» В ходе обсуждения студенты должны прийти к выводу, что задачи 6 и 7 основаны на действии сложения множеств, задача 8 основана на действии вычитания множеств, а задача 5 может интерпретироваться в зависимости от выбранной модели действия. Существенным в задачах 5, 6, 7 является только количество элементов в множестве, остальное несущественно. Разницы в моделях к задачам 6 и 7 нет.

После этого уже можно обсуждать и психологические вопросы. Например, можно задать вопрос: «А как ученики 1-го класса могут ответить на эти вопросы?» Тогда у студентов возникнет потребность в знаниях о психологии младшего школьника.

Пример 2б.

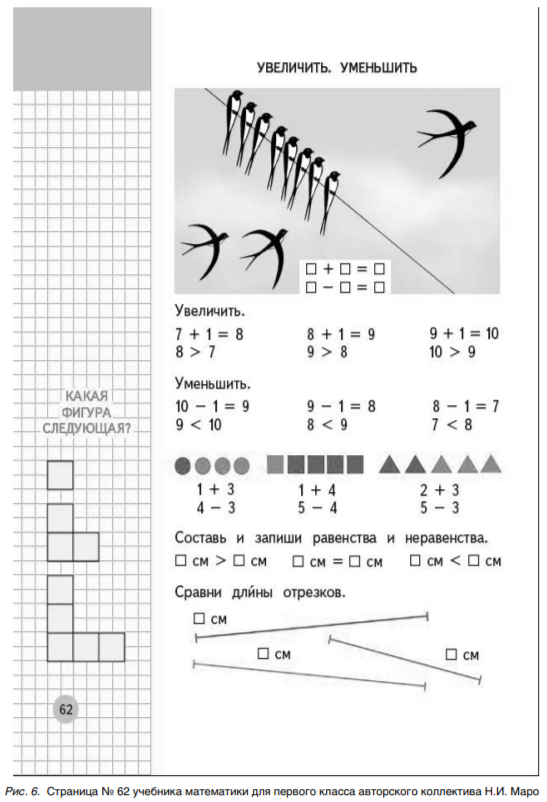
Студентам предлагается проанализировать задачу с ласточками на с. 62 из учебника Маро (см. рис. 6). Вопрос студентам: «При какой интерпретации смысла сюжетной картинки возникает необходимость воспользоваться понятием сложения множеств, а при какой - вычитанием множеств? Студенты легко отвечают на этот вопрос: «Например, когда две ласточки сядут на провод, то нужно воспользоваться объединением множеств, а если одна ласточка улетела с провода, то вычитанием множеств».

Тогда преподаватель может задать и творческий вопрос: «А как можно проинтер­претировать смысл картинки, чтобы появилась необходимость воспользоваться понятием пустого множества?» Предполагаемый ответ: «Ласточки пролетели мимо провода».

Пример 2в.

Студентам можно предложить проанализировать задачи на с. 52 (см. Рис. 7). Вопрос: «В каких задачах мы можем однозначно определить принадлежность элемента к множеству, а в каких - не можем без введения дополнительных условий?» Эту задачу можно задать на самостоятельную работу. На первый взгляд, все однозначно. Но если внимательно проанализировать задачу с покраской забора, то возникнет вопрос о том, как интерпретировать наполовину закрашенную доску - как уже закрашенную или как незакрашенную. В данном случае мы входим в область определения соотношения объекта и его модели (отображение существенных признаков объекта в модели) - принципиальный вопрос в науке и философии.

 Выводы

Рассмотренные нами примеры можно рассматривать как тренировку профессионального мышления педагога. В ходе выполнения таких заданий у студента должна развиваться методическая зоркость будущего учителя, понимание им основ действий ученика при решении внешне простых и незамысловатых задач. Современный учитель должен понимать фундаментальную сущность элементарных математических знаний. Поэтому для будущих учителей нужны труды по математике, образцом которых может служить выдающая книга Ф. Клейна «Элементарная математика с точки зрения высшей», написанная еще в начале прошлого века. Аналогичные пожелания можно высказать к методическому обеспечению преподавания естествознания, экономики, философии и т. д.

Вместе с тем наши ограниченные примеры показывают, что, как только мы вводим студентов в область формирования у младших школьников метапредметных компетен­ций, сразу всплывают проблемы психологического и философского характера, причем на уровне интерпретации действий учеников. Это остро ставит проблему содержания общей научной и общей гуманитарной подготовки будущих учителей. Узел этих проблем и одновременно ресурс повышения практической направленности теоретического обучения скрыт в той части учебной деятельности, где происходит преобразование чувственной формы объекта в модель, где выделены существенные характеристики объекта, а также преобразование модели для выявления общих законов, определяющих данную предметную область. В.В. Давыдовым было показано, что способность к осуществлению действий моделирования развивается в процессе решения так называемых учебных задач, т. е. задач, которые вынуждают ученика искать общий способ решения всех задач данного типа.

Студенты должны понять, что логика формирования знаково-символических действий как познавательных универсальных учебных действий связана с общей логикой решения задач квазиисследовательского типа. В ходе решения таких задач ученик приобретает опыт осмысления выделения существенных отношений в условиях задач и построения на их основе модели изучаемого объекта. Будущий учитель должен понимать, что переход от объекта к его модели не совершается сам по себе, что нужно подумать, какие свойства объекта нужно моделировать и для чего.

В процессе обучения студентов необходимо преодолеть традиционную школьную практику, когда учителя предлагают ученикам модель в готовом виде, не обсуждая условий и цели ее появления.

Финансирование

Подготовлено в рамках работ по исполнению государственного контракта № 05.043.11.0010 от 12 мая 2014 г. «Усиление практической направленности подготовки будущих педагогов в программах бакалавриата в рамках укрупненной группы специальностей ’’Образование и педагогика” по направлению подготовки ”Психолого-педагогическое образование” (Учитель начальных классов) на основе организации сетевого взаимодействия образовательных организаций, реализующих программы высшего образования и начального общего образования»