Диагностика уровня развития теоретического способа мышления у интеллектуально одаренных младших школьников

Таким образом, важной задачей является разработка диагностических критериев, которые могли бы служить показателями интеллектуального потенциала ученика. Мы предполагаем, что одним из таких показателей может выступать раннее развитие способности к теоретическому мышлению у учеников начальной школы, не проходящих специального обучения по системе Д.Б. Эльконина - В.В. Давыдова.

Особенности развития теоретического мышления у учеников начальных классов

Необходимое для овладения научным знанием теоретическое мышление при традиционном способе обучения, основанном на усвоении знаний по образцу, обычно развивается у младших школьников случайно. До этого у большинства детей в учебной деятельности преобладает эмпирический подход к изучаемому материалу, что не дает им возможности усматривать общие принципы и закономерности в изучаемых явлениях. В.В. Рубцов, рассуждая об отличии теоретического способа мышления от эмпирического и ссылаясь на работы В.В. Давыдова, пишет, что научно-теоретическое мышление отличается от рассудочно-эмпирического «способностью человека выделять генетически всеобщее отношение, некоторую всеобщую основу, определяющую конкретные свойства и отношения вещей до всякого непосредственного действия с этими вещами» [14, с. 53]. Таким образом, для теоретического мышления характерно выделение именно существенных признаков в изучаемом явлении, на основании которых ученик может произвести классификацию объектов и отнести их к определенной группе. В качестве объектов могут выступать задачи, решаемые учениками на уроке, вместе с учителем.

В.В. Давыдов сформулировал понятие учебной задачи, как задачи, которая вынуждает ученика искать общий (всеобщий) способ решения всех задач данного типа [5]. Показателем того, что ученик решил задачу теоретически, является то, что при ее решении он ориентировался именно на существенные отношения между элементами в ее условии. На основании выделенных существенных признаков в задаче ученик получает возможность отнести ее к определенному классу задач. Если ученик в процессе решения задачи мыслит на эмпирическом уровне, то такая классификация либо окажется невозможной, либо она будет осуществляться на основании внешних, не существенных признаков. В ходе решения учебных задач дети не только обучаются умению решать сходные задачи, но и осваивают способность выделять общие, существенные признаки, благодаря которым можно отнести задачу к определенной группе, для которой ученик уже овладел общим способом решения.

Таким образом, школьники в совместной деятельности с учителем и под его руководством учатся мыслить теоретически, выделяя существенные признаки в изучаемых явлениях. Показателем того, что ученик, решая задачу, выделил в ее условии именно существенные признаки, является то, что он способен решить все задачи определенного класса, независимо от внешних признаков в их условиях и количества необходимых для решения действий.

В исследованиях А.З. Зака было показано, что теоретическое мышление развивается у разных учеников с различной скоростью [6; 7; 9]. Им также была описана динамика развития теоретического мышления в начальной школе [8].

В ходе исследований, проведенных с учениками разных классов [9; 10; 13; 15], были выделены уровни сформированности отдельных компонентов теоретического мышления и соответственно его формы. Дифференциация функций анализа, планирования и рефлексии на различные стадии осуществлялась в этих исследованиях, в частности, на основании способа действия учеников при решении задач: насколько легко ими выделяются существенные признаки в условиях задач и осуществляется классификация тестовых заданий на определенные категории.

А.З. Заком были выделены и описаны три способа теоретического мышления [9]. Первый способ - аналитический, когда анализ (в теоретическом мышлении) играет ведущую роль, а рефлексия - вспомогательную (при выделении всеобщего отношения).

Второй способ - рефлексивный: при выделении особенных форм всеобщего отношения (специфических принципов решения подкласса задач данного класса) теоретическое мышление реализуется с помощью способа, в котором рефлексия имеет самостоятельную направленность. Третий способ - это способ, в котором рефлексия и анализ взаимосвязаны. Происходит выделение единства всеобщего отношения и его особых форм [9]. Чем более конкретной является задача, тем более совершенный способ теоретического мышления используется: аналитический по отношению к эмпирическому, рефлексивный по отношению к аналитическому. Отмеченные способы выступают тремя генетически преемственными формами теоретического мышления.

А.З. Зак пишет, что если у ученика уже в начальных классах наблюдается высокий уровень развития теоретического мышления или если данный способ мышления формируется у него достаточно быстро, то можно сделать предположение о том, что такой ученик обладает также и высоким уровнем развития общих интеллектуальных способностей [9].

В отечественной психологии исследования теоретического мышления и развития его отдельных компонентов (анализа, планирования и рефлексии) проводились В.А. Гуружаповым, А.З. Заком, Е.И. Исаевым, А.М. Медведевым, И.Н. Федекиным и другими учеными [1; 2; 3; 4; 8; 10; 13; 15]. В этих исследованиях были описаны: уровни сформированности отдельных компонентов теоретического мышления, различия в формах осуществления отдельных процессов и динамика развития теоретического мышления у школьников разных возрастов.

Гипотезы нашего исследования состояли в следующем: 1) результат решения задач на теоретическое мышление будет напрямую связан с уровнем развития интеллекта учеников;

2) ученики специализированной школы, прошедшие отбор при приеме в I класс, будут показывать более высокие результаты по методикам диагностики теоретического мышления, чем ученики в обычной школе; 3) методики теоретического мышления дают прогноз относительно дальнейшего развития общих интеллектуальных способностей именно у одаренных детей и не обладают возможностью прогнозирования в случае диагностики учеников со средним уровнем интеллекта.

Задачами нашего исследования были: определение связи между уровнями развития теоретического мышления и общих интеллектуальных способностей, динамики этой связи с I по IV классы и выявление различий данной связи у учеников специализированной и обычной средней школы. Таким образом, мы стремимся получить представление о том, в какой степени развитие теоретического мышления у учеников начальных классов может являться показателем их общих интеллектуальных способностей - как текущих, так и потенциальных.

В качестве методик диагностики теоретического уровня мышления нами использовались: задачи на диагностику теоретического мышления на непредметном материале А.З. Зака (серии «Различия», «Игры в 3» и «Почтальон») [6] и задачи на предметную диагностику теоретического мышления младших школьников на материале темы сложения многозначных чисел с переходом через разряд В.А. Гуружапова [1; 3]. Для диагностики уровня развития интеллекта мы применяли: Тест умственного развития (ТУР) и Групповой интеллектуальный тест (ГИТ) (автор обоих методик Г.П. Логинова) [11; 12].

Проводя диагностику по методикам А.З. Зака, экспериментатор сначала разбирал с учениками одну или две тренировочные задачи для того, чтобы ученики выработали общий принцип их решения. Затем они приступали к самостоятельному решению подобных задач. При этом количество действий в задачах постепенно возрастало, но внутреннее содержание и общий способ решения оставались неизменными.

Если ученик мыслит на эмпирическом уровне, то он еще не способен произвести содержательное обобщение, выделив общий принцип решения задач определенного класса, и, таким образом, овладеть способом решения всех подобных задач. К каждой задаче ученик будет подходить как к чему-то новому и заново конструировать способ решения. В таком случае ученик, скорее всего, не справится со всеми предложенными заданиями за отведенное для них время. По мнению А.З. Зака, если ребенок справился сразу со всеми предложенными ему задачами, то это значит, что он понял общий принцип их построения и в ходе решения осуществлял содержательный анализ их условий. Тем самым ученик реализовал в целом теоретический подход к решению. Если ученик не справился со всеми задачами, это значит, что им не был обнаружен принцип их построения, и, следовательно, учеником не был осуществлен содержательный анализ и теоретический подход к решению задач [7].

Нашу выборку составили ученики с I по IV классы двух московских школ: гимназии № 1514 (далее - гимназия) и обычной средней общеобразовательной школы. Количество учеников обычной средней общеобразовательной школы: II класс - 32; III класс 33; IV класс - 32 человека. Всего: 97 учеников. Количество учеников гимназии: I класс - 94; II класс - 82; III класс -75 человек. Всего: 169 человек. Все ученики гимназии при приеме в I класс прошли предварительный отбор и могут считаться интеллектуально одаренными детьми.

По результатам исследования можно выделить три уровня успешности решения задач на теоретическое мышление. Они соответствуют уровням, выделенным в исследованиях, проведенных А.З. Заком.

Низкий уровень - ученик либо не решил правильно ни одной задачи определенной группы, либо справился только с одной (как правило, с самой первой).

Средний уровень - ученик решил больше половины задач определенной группы, но с последними двумя задачами в сериях «Различия» и «Игры в 3», и последними тремя задачами в серии «Почтальон» не справился либо решил их неверно. Такой результат говорит о том, что ученик в ходе решения определенной серии задач руководствовался эмпирическим способом мышления. Им не было выделено общих принципов решения.

Высокий уровень - ученик правильно решил все задачи определенной группы. Это является показателем того, что учеником был осуществлен теоретический подход к решению задач.

Часто у учеников, которые не смогли правильно решить ни одну задачу, в тестовых бланках были записаны все решения, но ни одно из них не было верным (особенно часто это встречалось в группе задач «Почтальон»). Это - показатель того, что ученик не смог понять правила решения задач из их условия и при разборе с экспериментатором тренировочных задач. Такой результат также был отнесен нами к низкому уровню.

Всего ученикам для самостоятельного решения нами было предложено 17 задач непредметной диагностики теоретического мышления, разработанных А.З. Заком: 5 задач в серии «Различия»; 5 задач «Игры в 3» и 7 задач «Почтальон». Количественно мы определили описанные выше три уровня успешности решения этих задач следующим образом: низкий уровень - верно выполнены 0-6 задач; средний уровень - 7-12 задач; высокий уровень - 13­17 задач.

Для задач предметной диагностики теоретического мышления на материале темы сложения многозначных чисел с переходом через разряд и задач серии «Башня» также выделялись три уровня решения: низкий, средний и высокий. Далее результаты по этим двум методикам переводились в баллы (низкий - 0 баллов, средний - 1 балл, высокий - 2 балла) и суммировались. Подробные описания критериев этих уровней приведены В.А. Гуружаповым в соответствующих работах [1; 3]. Результаты решения задач на теоретическое мышление учениками гимназии и обычной средней школы представлены в табл. 1.

Таблица 1

Количество учеников с разным уровнем успешности решения задач А.З. Зака на диагностику теоретического способа мышления

Из табл. 1 видно, что в гимназии к III классу большинство учеников при решении задач показали высокий уровень, соответствующий теоретическому способу мышления. В обычной средней школе большинство учеников решали предложенные задачи эмпирически.

В табл. 2 представлены данные о средних значениях по всем проведенным методикам.

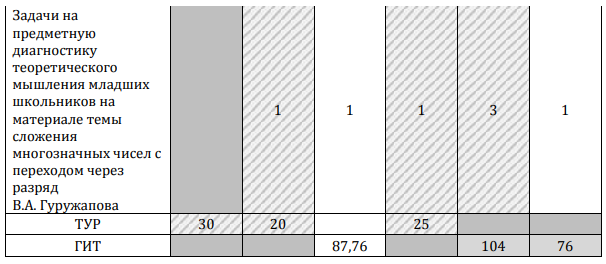
Мы видим, что средние значения результатов по всем тестовым методикам (кроме задач на предметную диагностику теоретического мышления В.А. Гуружапова во II классах) в гимназии выше, чем в обычной школе. Особое внимание следует обратить на то, что средний балл по задачам на теоретическое мышление А.З. Зака в III классе гимназии в два раза выше среднего балла в III классе обычной средней школы.

Различия в средних результатах решения задач на теоретическое мышление В.А. Гуружапова еще более существенны. Средние результаты по интеллектуальным методикам дают немного менее очевидные различия.

Далее нами был проведен статистический анализ различий средних результатов по всем тестовым методикам между обычной школой и прогимназией по t-критерию Стьюдента (табл. 3).

Таблица 3

Данные о значимости различий результатов тестирования учеников в разных классах по t-критерию Стьюдента

Были выявлены статистически значимые различия по всем проведенным методикам между результатами в обычной школе и в гимназии. Не было выявлено статистически значимых различий только между результатами диагностики теоретического способа мышления по задачам А.З. Зака между I классами гимназии и III классами обычной школы.

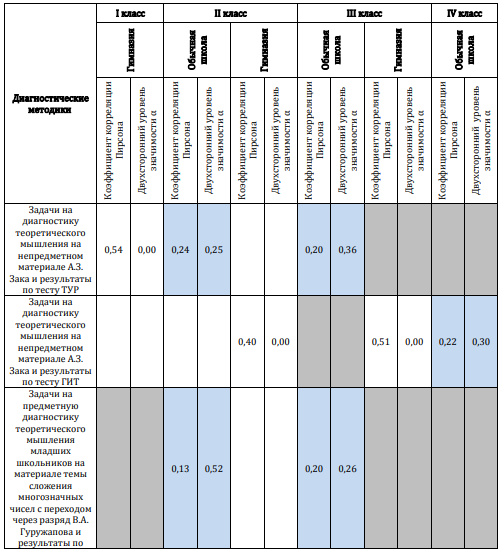
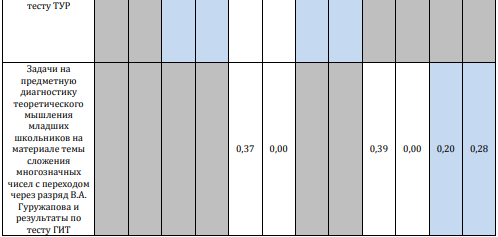
Далее нами был проведен анализ корреляций между результатами используемых нами методик (табл. 4).

Таблица 4

Анализ корреляции между количеством правильно решенных задач на теоретическое мышление А.З. Зака и В.А. Гуружапова и результатами по тестам ТУР и ГИТ

Обсуждение результатов

Результаты анализа значимости различий по Т-критерию Стьюдента и корреляционного анализа дают основания для вывода о том, что методики диагностики теоретического мышления могут быть использованы для выявления одаренных учеников с высоким уровнем развития интеллекта и для осуществления примерного прогноза относительно их дальнейшего развития.

В качестве побочного результата мы выявили, что в IV классах обычной средней школы вообще нет связи между развитием интеллекта и теоретическим мышлением. Видимо, само по себе теоретическое мышление не развивается при традиционной системе обучения.

Заключение

Таким образом, уровень развития теоретического мышления может рассматриваться как показатель одаренности учеников в начальной школе. У одаренных учеников уровень развития теоретического мышления напрямую связан с интеллектом, и эта связь значительно сильнее, чем у обычных учеников начальных классов средней школы. Сами методики диагностики теоретического уровня мышления менее трудоемки. Для их проведения и обработки требуется меньше времени, чем для интеллектуальных тестов, а результаты, полученные с их помощью, могут быть использованы для определения уровня развития общих интеллектуальных способностей у учеников начальной школы.

Способность решать учебные задачи на теоретическом уровне мышления у учеников младших классов без специального обучения может выступать как один из показателей одаренности и заслуживает особого внимания. Необходимо проведение дальнейших исследований связи уровня развития отдельных компонентов теоретического мышления (анализа, планирования и рефлексии) с общими интеллектуальными способностями учеников начальной школы и ее возрастной динамики.