Подготовка учителя начальных классов к профессиональной деятельности по развитию математического мышления младших школьников

В статье рассматривается один из аспектов подготовки педагога начального общего образования – умение анализировать причины ошибок обучающихся, допускаемых ими при усвоении математических понятий. Отмечается особое значение в компетентности учителя начальных классов понимания ценности исходных, первоначальных представлений ребенка как результата его собственной мыслительной деятельности. Дается обзор понятия математического мышления в психолого-педагогической литературе. Выделяется понимание математического мышления как теоретического, осуществляемого на математическом материале. Фиксируются уровни развития математического мышления и его основных компонентов – анализа, планирования и рефлексии. Описываются модули образовательной программы подготовки учителей начальных классов, направленные на развитие у студентов компетенций, позволяющих адекватно оценивать проявления математического мышления у младших школьников на математическом материале, традиционно изучаемом в начальной школе. Представлена последовательность действий, направленных на выявление шаблона ошибки. Приводятся примеры заданий для студентов, показывающие способы развития учебного действия контроля; определения шаблонов математических ошибок.

Математическое мышление как метапредметный образовательный результат начального образования

В российском педагогическом образовании происходят существенные изменения, определяемые качественными преобразованиями в системе общего образования [7; 9; 15]. Приоритетной целью отечественного общего образования становится личностное и познавательное развитие обучающихся. В развивающем образовании происходят изменения в целеполагании и характере педагогической деятельности: качественное усвоение предметных знаний становится здесь условием и средством развития метапредметных умений, универсальных учебных действий и возрастных новообразований [3; 17]. Центральными новообразованиями младшего школьного возраста определены теоретическое мышление и субъектность учебной деятельности – умение учиться [5; 19; 21]. В системе развивающего обучения Д.Б. Эльконина и В.В. Давыдова ключевая роль в развитии теоретического мышления отводилась учебному предмету «математика» [6].

В психолого-педагогическом сообществе широко обсуждаются вопросы развития математического мышления младших школьников в процессе обучения, а также вопросы подготовки учителя, способного обеспечить это развитие [1; 8; 13; 22]. Особую актуальность данные исследования приобрели в условиях введения федеральных государственных образовательных стандартов, призванных обеспечить математическое развитие младшего школьника – формирование способности к интеллектуальной деятельности, пространственного воображения, математической речи.

Методика развития исходных представлений обучающихся до научных понятий предусматривает подход в обучении, связанный с преимуществом развития концептуальных знаний над процедурными знаниями. Исходные представления детей, с которыми они приходят в школу, являются основой их актуального уровня предметного мышления, определяют необходимость видеть в ошибочных представлениях возможность их развития и осознания концептуальных оснований своих действий [10].

Осваивая программу начального общего образования по математике, обучающиеся встречаются с широким спектром понятий: натуральное число, разряд, класс, система счисления, число нуль, доли, арифметические действия, равенство, неравенство, уравнение, задача. Предусмотрено изучение различных геометрических фигур, величин и единиц измерения величин. В той или иной мере у обучающихся есть исходные представления о данных понятиях, развитие которых будет обеспечивать развитие математического мышления.

Математическое мышление определяют с помощью различных характеристик. Это гибкость, оригинальность, присутствие творческого воображения, лаконизм, логичность и другие.

В.А. Крутецкий выделял в структуре математических способностей обобщенное, свернутое и гибкое мышление в сфере математических отношений, числовой и знаковой символики; способность к формализованному восприятию математического материала, схватыванию формальной структуры задачи; к быстрому, широкому, детальному обобщению математических объектов, отношений и действий, к обратимости мыслительных процессов, к свертыванию процесса математического рассуждения и системы соответствующих действий (способность мыслить свернутыми структурами), к пространственным представлениям; способность к быстрой и свободной перестройке направленности мыслительного процесса, переключению с прямого на обратный ход мысли; стремление к ясности, простоте, экономности и рациональности решений; особую обобщенную память на математические отношения, схемы рассуждений и доказательств, методы решения задач и принципы подхода к ним [12, с. 375].

Особое понимание математического мышления имеется в работах Ж. Пиаже. Он считал, что существует особое логико-математическое мышление. Мышление – система операторных структур. У ребенка формируются средства отделения действий от объектов, а затем возникает особая логика этого отделения и оперирования его результатами, т.е. абстракциями, идущими от самих действий. Именно внутри этой логики интеллект ребенка приобретает свойство обратимости. «Логичность» мышления связана с выполнением ребенком обратимых операций, абстрагированных от самих действий, а «математичность» связана с тем, что этим операциям соответствуют такие математические структуры, как алгебраические, топологические и порядка. Развитие математического мышления – это развитие операторных структур [16]. Таким образом, для Ж. Пиаже математическое мышление – это любое мышление, которое связано с ориентацией на абстракции от действий, в отличие от абстракций от непосредственных свойств предметов.

И.Я. Каплунович и Т.А. Петухова, исследуя математическое мышление, выделяют в его структуре пять пересекающихся основных подструктур, находящихся в определенной зависимости, иерархии по степени значимости и представительности в интеллекте: топологическую, порядковую, метрическую, алгебраическую и проективную. Они считают, что можно определить наиболее ярко выраженную, ведущую подструктуру, в соответствии с которой человек по-разному воспринимает, оперирует, перерабатывает и воспроизводит математическую информацию [11].

Л.М. Фридман считает, что специфические черты и особенности математического мышления обусловливаются спецификой изучаемых при этом объектов [20, с. 40]. Математические объекты лишены любых вещественных (материальных) и энергетических характеристик, имея лишь одну характеристику: эти объекты находятся в определенных отношениях друг к другу, в отношениях количественных, пространственных и им подобным. Он определяет математическое мышление как «предельно абстрактное, теоретическое мышление, объекты которого лишены всякой вещественности и могут интерпретироваться самым произвольным образом, лишь бы при этом сохранялись заданные между ними отношения» [20, с. 41].

Исследования математического мышления в русле теории В.В. Давыдова о типах мышления проведены Л.К. Максимовым и Р. Атахановым.

Работа Л.К. Максимова была посвящена изучению содержания и особенностей математического мышления как мышления теоретического типа. «Мышление человека в некотором предметном содержании требует соответствующей этому содержанию формы. С другой стороны, владение человеком определенной формой мышления позволяет ему успешно ориентироваться в предметном содержании. В том случае, когда мышление, используя свои формальные возможности, превращает себя в какое-то определенное содержание, например, математическое, оно становится математическим мышлением. Математическое мышление является формой теоретического мышления, проявляющегося на математическом содержании» [14, с. 56–57].

Таким образом, Л.К. Максимов считает, что математическое мышление выступает как один из видов мышления теоретического типа, а его содержанием является преобразование математического материала при осуществлении мыслительных действий содержательного анализа, планирования и рефлексии. Другими словами, на основе того, на каком материале проявляются основные компоненты теоретического мышления – на математическом, физическом, химическом и т.д., целесообразно различать соответственно математический, физический, химический, а также другие виды мышления. Вопрос о развитости математического мышления решается выявлением особенностей развития (наличия или отсутствия) основных компонентов теоретического мышления – анализа, планирования и рефлексии.

Р. Атаханов, исследуя психологические особенности математического мышления, показал наличие уровней развития математического мышления и описал их психологические характеристики. Он определил математическое мышление как такой вид мышления, который «осуществляется на материале, формализуемом при помощи математических способов ориентации в количественных отношениях действительного мира» [2, с. 15]. Р. Атаханов приходит к выводу, что становление математического мышления обусловливается развитием мышления вообще, характеризуется наличием эмпирического и теоретического типов, а также соответствующих им уровней. Развитое математическое мышление есть теоретическое мышление. Мышление теоретического типа, в том числе математическое, имеет аналитический, планирующий и рефлексирующий уровни развития. Сформированность теоретического уровня математического мышления проявляется в умении осуществлять мыслительные действия анализа, планирования и рефлексии на математическом материале. Уровень развития математического мышления базируется на сформированных уровнях теоретического мышления более общего плана (мышления вообще). Уровень развития математического мышления школьника на определенном этапе ограничен уровнем развития у него мышления вообще [2].

Таким образом, единого общепринятого определения математического мышления пока не выработано. Мы будем придерживаться идейно близких нам определений Л.К. Максимова и Р. Атаханова: математическое мышление является формой теоретического мышления, проявляющегося на математическом содержании и осуществляемого на математическом материале. Применительно к содержанию программы по математике в общеобразовательной школе его можно рассматривать как владение способами ориентации в количественных отношениях действительного мира. Вопрос о развитости математического мышления решается выявлением особенностей развития основных компонентов теоретического мышления – анализа, планирования и рефлексии, проявляющихся при решении математических задач.

В.А. Крутецкий, исследуя проблему развития математических способностей, обнаружил, что большинство школьников обобщает решение математических задач только путем постепенного и длительного сравнения. Наряду с этим «путь постепенного обобщения не является единственным, ведущим к усвоению знаний по математике… Существует и другой путь, когда способные ученики, не сопоставляя “сходное”, не сравнивая, без специальных упражнений и указаний учителя осуществляют самостоятельно обобщение математических объектов и отношений, действуя “с места” на основании анализа лишь одного явления в ряду сходных явлений» [12, с. 288]. В.А. Крутецкий не квалифицирует описанные им виды обобщения как «эмпирическое» и «теоретическое». Он считает, что они коренятся в такой ориентации некоторых людей на математические зависимости, которая имеет врожденный характер: «… мозг некоторых людей своеобразно ориентирован (настроен) на выделение из окружающего мира раздражителей типа пространственных и числовых отношений и символов и на оптимальную работу именно с такого рода раздражителями» [12, с. 385–386].

Анализируя данные В.А. Крутецкого (об обобщении математических объектов и отношений «с места»), В.В. Давыдов отмечает, что в его исследованиях «экспериментально констатировано различие эмпирического и теоретического обобщения в мыслительной деятельности школьников, различие путей и средств их реализации, а также их познавательной эффективности. Особенности каждого вида обобщения находят свое правильное объяснение в раскрытии их функции внутри двух различных типов мышления – эмпирического и теоретического» [4, с. 251].

Роль учителя в развитии исходных представлений обучающихся до научных понятий

Особое значение в методике развития исходных представлений обучающихся до научных понятий отводится пониманию учителем ценности представлений ребенка как результата его собственной мыслительной деятельности. Такой учитель способен видеть потенциал развития исходных представлений до научных понятий, способен обнаружить особенности математического мышления ребенка и сделать исходные представления предметом специальной работы по их развитию [10].

Подготовка учителей начальных классов в МГППУ ведется на основе модульного принципа построения образовательной программы. Изучению модулей, в которых рассматривается методика преподавания отдельных предметов, предшествует изучение общих основ теории учебной деятельности. В рамках данного модуля студенты – будущие учителя начальной школы – знакомятся с таким содержанием: классификация В.В. Давыдова видов мышления (эмпирическое и теоретическое); основные компоненты теоретического мышления (анализ, планирование, рефлексия); примеры диагностики основных компонентов теоретического мышления; задача проектирования методик предметной диагностики теоретического мышления; основные принципы конструирования заданий для диагностики действия анализа; примеры предметной диагностики действия анализа; самостоятельное проектирование задания на диагностику анализа; основные принципы конструирования заданий для диагностики действия рефлексии; примеры предметной диагностики действия рефлексии; самостоятельное проектирование задания на диагностику рефлексии; основные принципы конструирования заданий для диагностики действия планирования; примеры предметной диагностики действия планирования.

Уже в этом модуле студенты получают возможность обсуждать следующий вопрос: демонстрируют ли младшие школьники умение обнаружить общий способ действия при решении учебных задач и при выполнении различных заданий, в том числе и на предметном математическом материале.

Например, рассматриваются и обсуждаются различные способы выполнения одного и того же задания разными учащимися.

Задание 1. Найдите не равные нулю слагаемые по известной сумме и указанному числу слагаемых:

  5=…+…

  7=…+…+…

  9=…+…+…+…

11=…+…+…+…+…

13=…+…+…+…+…+…

15=…+…+…+…+…+…+…

17=…+…+…+…+…+…+…+…

19=…+…+…+…+…+…+…+…+…

21=…+…+…+…+…+…+…+…+…+…

Ниже приводятся типичные ситуации, возникающие при выполнении этого задания.

Первый ученик выполнил задание так:

  5=3+2

  7=1+4+2

  9=3+2+1+3

11=2+3+1+3+2

13=5+2+3+1+1+1

15=8+2+1+1+1+1+1

17=5+5+1+1+2+1+1+1

19=3+2+3+2+3+2+1+1+2

21=5+5+1+1+1+1+1+2+2+2

Второй выполнил так:

  5=3+2

  7=1+4+2

  9=3+2+1+3

11=3+2+1+3+2

13=3+2+1+3+2+2

15=3+2+1+3+2+2+2

17=3+2+1+3+2+2+2+2

19=3+2+1+3+2+2+2+2+2

21=3+2+1+3+2+2+2+2+2+2

Третий выполнил так:

  5=3+2

  7=3+2+2

  9=3+2+2+2

11=3+2+2+2+2

13=3+2+2+2+2+2

15=3+2+2+2+2+2+2

17=3+2+2+2+2+2+2+2

19=3+2+2+2+2+2+2+2+2

21=3+2+2+2+2+2+2+2+2+2

Обсуждая представленные решения, легко прийти к очевидным выводам, которые делают сами студенты. Первый ученик демонстрирует эмпирический способ решения задачи. Он не находит общего способа действия и к каждой строчке подходит как к отдельной задаче, не обнаруживая связь между математическими выражениями. В решении второго ученика мы видим начиная с четвертой строки проявление общего способа действия. Им обнаружена связь, но не сразу. А третий ученик сразу начинает действовать общим способом. Про него можно сказать словами В.А. Крутецкого, что он проявил обобщение «с места», сразу выявив закономерность в построении математических выражений.

Приведем пример на математическом материале, который иллюстрирует проявление действия рефлексии как компонента теоретического мышления.

Задание 2. Реши примеры.

        1              2               3

    449           435            449

 –   32       –    18       –     52

Какие примеры похожи?

Далее со студентами обсуждается методический комментарий к этому заданию. Выполнение задания состоит из двух этапов. Сначала нужно выполнить обычное вычитание в столбик. При вычитании получаются ответы: 417, 417, 397. Нас интересует, какие примеры школьник выберет в качестве похожих. Похожи примеры 1 и 2 – у них одинаковые ответы 417. Похожи примеры 1 и 3 – у них одинаковые уменьшаемые 449. Но это внешняя похожесть, а есть ли схожесть в способе решения? Это и есть рефлексивный момент данного задания. Вычитая в примере 1, нам не нужно занимать у единиц старшего разряда. А в примерах 2 и 3 при вычитании нужно занимать. Поэтому с точки зрения способа решения похожи примеры 2 и 3. Большинство же детей выбирает примеры 1 и 2 с одинаковыми ответами. Таким образом, можно констатировать, что большинство детей, вычитая, ориентируется на внешнюю схожесть, но не на способ действия.

Завершая со студентами обсуждение задания 2, мы фиксируем общий способ построения заданий на проявление рефлексии как компонента математического мышления: для проявления рефлексии предлагается серия задач, одни из которых одинаковы по принципу решения (примеры 2 и 3), но отличаются по внешним признакам, другие (примеры 1 и 2, 1 и 3) – похожи этими внешними признаками, но имеют различные принципы решения.

Целью освоения программы модуля «Содержание и методы обучения в предметной области “Математика и информатика”» является формирование у бакалавров способности к реализации программ обучении и развития младших школьников в предметной области «Математика и информатика», направленной на достижение личностных, метапредметных и предметных образовательных результатов обучающихся в соответствии с требованиями федерального государственного образовательного стандарта начального общего образования.

Один из содержательных разделов модуля – «Типовые ошибки обучающихся на уроках математики». Данный раздел рассматривается нами как возможность показать студентам взаимную связь между шаблонами ошибок, которые допускают младшие школьники, с неверными представлениями детей о математических понятиях и процедурах. Акцент делается на следующем положении: при проверке работ учащихся необходимо не просто отметить встречающуюся ошибку, но провести диагностическую оценку, определив, какие виды ошибок делает ученик и почему. В частности, диагностическая оценка должна позволить выявить, существует ли шаблон ошибки, то есть допускает ли тот или другой ученик ошибки одного и того же вида. Если такой шаблон действительно существует, учитель может выявить заблуждения учащегося или дефицит навыков, а затем разработать и реализовать план для устранения проблемы конкретного ученика. Такой подход позволяет индивидуализировать обучение, а своевременная коррекция неправильных представлений, проявляющихся в шаблонах ошибок, способствует развитию учащегося, в том числе развитию его математического мышления.

Фундаментальное исследование Р. Эшлока [23], посвященное анализу шаблонов ошибок (error patterns) в вычислениях, демонстрирует коллекцию различных видов ошибок, встречающихся у учащихся в процессе изучения математики. Исследование призвано помочь учителям выявить распространенные математические ошибки у детей и получить представление о том, почему ребенок мог усвоить неправильный математический алгоритм действия.

Р. Эшлок различает неосторожные ошибки, которые мы все совершаем, и неправильные представления о математических идеях и процедурах, которые приводят к появлению типичных ошибок. Он полагает, что в процессе изучения нового понятия ученики сосредотачиваются на своем имеющемся опыте, ищут в нем то общее, что связано с новым понятием, связывают новую информацию с тем, что они уже знают. Однако такое предварительное знание не всегда является правильным, что может привести к ошибочному усвоению нового знания.

Сбор данных об ошибках ученика должен предусматривать выполнение специально подобранных заданий, теста или контрольной работы, содержащих ряд однотипных заданий. Данные для анализа ошибок могут быть собраны с помощью формальных процедур, например, самостоятельная работа, тест, или неформальных, например, домашнее задание, при условии, что учитель уверен, что ученик выполнил задание самостоятельно.

Анализ ошибок является одной из форм диагностической оценки. Собранные данные могут помочь учителям понять, почему у учащихся не получается добиться успеха при выполнении определенных заданий и построить дальнейшее обучение с учетом конкретных потребностей учащегося.

Для того чтобы можно было определить шаблон ошибки, задания при сборе данных должны содержать как минимум от трех до пяти заданий одного типа. Это позволяет иметь достаточное количество элементов для анализа и определения шаблона ошибки.

Чтобы лучше понять, почему учащиеся испытывают трудности, учитель должен отметить каждую неправильную цифру в решениях ученика, а не просто отметить весь ответ как неправильный. Внимание к каждой цифре в ответе ученика позволит учителю быстро и четко определить ошибку ученика и понять: постоянно ли ученик совершает эту ошибку при выполнении действия [18].

Приведем пример задания на поиск шаблона ошибки по теме «Письменное вычитание».

Задание 3. Ученик решил четыре примера, результат его работы перед вами. Определите, какая ошибка повторяется во всех действиях ученика.

   843        471         703        700

– 657       – 36      – 586     – 236

   214        445         283        536

Здесь несложно обнаружить шаблон ошибки данного ученика: вычитание производится по разрядам, но по принципу «что вычитается». Если из единиц уменьшаемого разряда нельзя вычесть единицы вычитаемого разряда, то вычитаем наоборот. Другими словами, ученик вычитает из большего числа меньшее.

Данная ошибка показывает, что учащимся не усвоен общий прием письменного вычитания в столбик, то есть алгоритм вычитания усвоен формально, со стороны его внешней формы. Следовательно, для преодоления этой ошибки нужно вернуться к конструированию общего способа действия, рассмотреть связь между производимыми при вычитании действиями с разрядами и отображением этих действий в записи столбиком. Возможно, нужно вернуться еще на шаг назад и обратиться к предметной основе действия вычитания многозначных чисел, рассмотреть это действие, используя модели чисел.

Обсуждая данные проблемные вопросы со студентами, мы стремимся сформировать у них подход к обучению математике, обеспечивающий овладение учащимися общим способом действия.

Развитие теоретического мышления происходит в процессе решения учебных задач. Учебная задача решается посредством выполнения учебных действий. Таким образом, внимание к развитию учебных действий обеспечивает в конечном счете и развитие математического мышления как мышления теоретического типа.

Поиск ошибок в решенных другими детьми заданиях вносит вклад в развитие учебного действия контроля. Контроль позволяет, меняя операционный состав действий, выявлять их связь с особенностями условий задачи и свойствами получаемого результата, обеспечивает нужную полноту операционного состава действий и правильность их выполнения [5].

Таким образом, мы стремимся научить студентов конструировать задания с ошибками, обеспечив при этом понимание особенностей такого задания: это должно быть действие, состоящее из нескольких операций, при этом ошибки должны быть допущены при выполнении разных операций. Тем самым мы обеспечиваем внимание учащихся к каждой операции. Рассмотрим одно из подобных заданий.

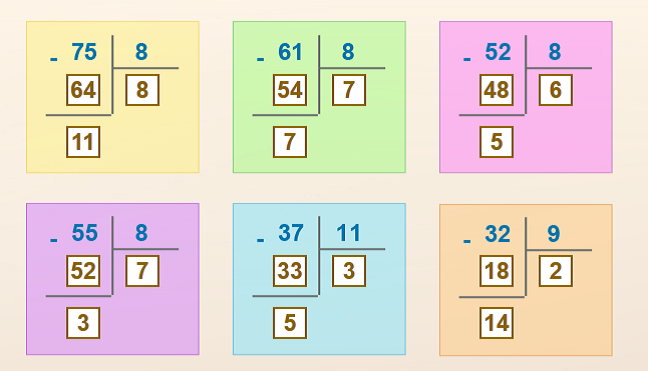
Задание 4. Проверь, правильно ли выполнено действие столбиком. Исправь записи (см. рис.).

Рис. Задание 4

Далее со студентами обсуждается следующий методический комментарий к этому заданию. Действие деления с остатком способом подбора подходящего частного состоит из трех операций: 1) подбор частного, 2) умножение частного на делитель, 3) вычитание из делимого результата умножения (неполного делимого). Задание с ошибками для формирования учебного действия контроля состоит из шести примеров. Рассматриваем примеры, двигаясь по строчкам слева направо. В первом примере умножение и вычитание выполнены верно, но остаток больше делителя, значит, неверно подобрано частное. Во втором примере допущена ошибка в умножении. В третьем примере – ошибка в вычитании. Далее: в четвертом – ошибка в умножении, в пятом – в вычитании, в шестом – в подборе частного. Таким образом, внимание детей фиксируется на каждой операции сложного действия, что обеспечивает осознанность изучения алгоритма деления с остатком. Упражнение выполняется фронтально после того, как учащиеся уже освоят прием деления с остатком подбором подходящего частного. Необходимо обсудить все виды возможных ошибок в действии.

Данная статья была посвящена демонстрации новых методик обучения студентов. По нашему замыслу представленные задания способствуют решению следующих задач программы обучения студентов:

– понимание математического мышления как теоретического мышления, осуществляемого на математическом материале;

– понимание проявлений основных компонентов математического мышления – анализа, планирования и рефлексии – на математическом материале, традиционно изучаемом в начальной школе;

– понимание связи учебных действий, в том числе действия контроля, с формированием общего способа решения математических задач;

– умение выявлять шаблоны ошибок для своевременной коррекции неправильных представлений учащихся о математических понятиях и процедурах.

Дальнейшей задачей нашего исследования является диагностика результатов обучения студентов по реализуемой программе.

1. Ассонова Н.В. О нематематической составляющей понятия «математическое развитие младшего школьника» // Актуальные вопросы профессиональной подготовки современного учителя начальной школы. 2021. № 8. С. 3–10.