Formation of concept of decimal system in Mexican school children

Introduction

In Mexico, the way mathematics is thought is a matter of great importance since the level of children’s knowledge in this area is very low (SEP, 2011). This means that pupils of third grade of primary school can only solve exercises with low degree of difficulty (elementary operations, increasing sequence with an additive constant, to identify the predecessor of a number, etc.). The teaching method proposed by Secretariat of Public Education (2011) emphasizes that the teacher's task is to create learning environments in order to make pupils think about the methods that perform, promote communication of mathematical ideas that arise during class and evaluate the level of skills that students develop. Nevertheless, no conceptual knowledge is included in current methodology for mathematics. Secretariat of Public Education only proclaims the necessity of reflection, but there are no real proposals which could support such proposition.

Recent research shows how some kinds of mathematical skills that pupils have developed the first grade. Such skills are: follow a command of verbal and numerical sequence counting process, recognition of the properties of closed numbers (tens, hundreds, thousands units), writing by dictation extended numbers (for example, one thousand five hundred-1000500), reading the carried quantities on numbers segmenting one or two digits and solving of addition problems. All such kinds of operations is achieved without any precise knowledge of decimal number system nor of the formal algorithm. Some studies show that the only strategy used by children in primary school during solution of exercises is counting by fingers, personal drawings and mental calculations (Castaneda, 2008; Buto y Gomez, 2011; Garcia, 2011). It is possible to argue that such level of operations is related to empiric mechanic execution.

The introduction of Decimal System concept represents one of the essential aspects of learning at primary school. This is the theme which occupies most of the activities in the first three years of primary school education (Ruesga y Guimaraes, 2011). The decimal number system is considered a positional system, because the figures are not independent but are subject to their position (Silva y Barela, 2010; Avila y Garcia, 2008; Luria, 1995). Each new column of the decimal number system is considered as a new measure count, which is 10 times greater than the extent of the previous column, for example, 10 units of the first column (units) given unit of the second column (tens). The reflection of such relationships could allow students show arithmetic actions, laws and combination translational. It is also possible to emphasize that counting by equal groups (not necessary by 10 units), allows preparation of the conceptual introduction of multiplication. Subsequently division could be shown to the children as the action contrary to the multiplication. Showing the principles of construction of numbering system makes them able to create new measurements of counting, working with the network of columns of numbers (M, C, D, U). Continuation of this logic permits to introduce fractions and decimal fractions at the next step (Talizina, 2009, Salmina, 2001).

The Activity Theory applied to the process of school education (Talizina, Solovieva and Quintanar, 2010; Solovieva and Quintanar; 2010; Galperin, 2009; Talizina, 2009; Salmina, 2001) shows that in order to allow children to assimilate and generalize academic content, teaching should be done through the following stages: 1) stage of motivation, 2) guide based on the action, 3) material-materialized stage, 4) perceptual stage, 5) external speech stage, 6) the internal language stage. Specific types of such actions should be proposed for assimilation of Decimal System concept. Specifically, mathematic content is organized around four components: logical, symbolic, mathematical and spatial (Salmina y Filomonova, 2002; Solovieva, Ortiz y Quintanar, 2010; Solovieva, Quintanar & Ortiz, 2012).

The objective of our study consisted in implementation of methodology of formative experiment and gradual formation of scientific concepts for the theme of decimal concept in primary school. The work was fulfilled by post graduated student of Master in Neuropsychology of Faculty of Psychology of Autonomous University of Puebla. The work represents a part of Master Dissertation of this institution, elaborated and carried out together with professors of the Program.

Method

Participants

Children of second grade of elementary school were included in formative experiment. The average age of the children was 7.25 years. The requirements to be able to participate in the experiment were: Being in 2ndgrade of elementary school for the first time, and do not present neurologic background. The table 1 shows the characteristics of the participants.

Table 1. Description of the participants

Workspace

The experiment took place in a small new private college, located in the city of Puebla, Mexico. The figure 1 represents the workspace.

Material

The protocol “Verification del exito escolar en la escuela primaria” (Solovieva y Quintanar, 2003), based on Luria's conception of High Psychological Functions, was applied. Also, tasks of measure comparison, arithmetic problems resolution, addition and subtraction were included. The figure 2 presents some examples of the initial evaluation test.

The same tasks were applied in the final evaluation and others with higher complexity, some examples are shown in the figure 3.

Experiment

A formative experiment concept was used according to the authors of historical and cultural psychology (Talizina, 1998; Salmina, 2001, Talizina, Solovieva y Quintanar, 2010). In such studies the method consists of gradual formation of concepts, skills or actions starting from level “0”, that is, providing gradual cooperation within the zone of proximate development, according to L.S. Vigotsky’s conception. The formation is organized and guided by an adult who knows the operative structure and all kinds of necessary orientation which can guarantee reflective and conscious acquisition of proposed concepts. At the end such skills are tested in common and new tasks which are proposed to children.

At the same time an experimental design was used.

G1: O1 X O2

G1= experimental grup; O1= Pretest; X= teaching method; O2= Postest.

Procedure

The divided collective activity in groups and in pairs of children was considered for all steps of the program. The actions with measuring of magnitudes and work with different objects were included. The program includes specific tasks for symbolic, logical, numeric and spatial component. The Program was applied 3 days per week during six months. In the following table (2) the thematic, objectives, and materials of the teaching method are shown.

Table 2. Tasks of teaching method

Subject 1. Measure: Measurements were performed considering various objects and magnitudes. Specific concepts like “Magnitude”, “Measure” and “Number” were introduced and explained to children form the very beginning (the figure 4 shows the orientation card for this task). In this case, “Number” corresponds to the quantity of times a measurement is used. These elements are described in the card "Measure", where children had to use this card for every concrete example. Firstly, they chose an object and a feature of an object to measure (e.g. a highness or broadness of a toy, window, board, distance between two places in the classroom or between tow children, water bottles) and something with which we can to measure such objects (pencils, chalks, paper strips, glasses and so on). The measurement of volumes of different liquids with the help of specific measures was used as well. Subsequently, the gathered data was written down on the students notebooks using the "Measurement Scheme". The Figure 5 shows an example of a task of the materialized stage, in which a drawn path is measured using a paper foot.

Subject 2. Teaching of unit: In this stage, every task was performed using a common measurement to compare different objects and liquids. In this case, the size to be measured was chosen by all the participants (the same ribbon).The goal was to teach children that the smaller was the size of the measurement, the more times they would have to use it, and the other way around, the bigger was size of the measurement the lesser times they would have to use it. The Figure 6 shows how our children measured distances (“Magnitude”) between various objects or places. In some exercises children had find out which roads where longer or shorter. Matches were used by children to represent the quantity of times the measurement (a ribbon) was used. All data was recorded on the board and a comparison was made between the paths and lines in all occasions. The children used mathematical signs “less than” (<), “greater than” (>) and “equal” (=) to understand the relationships between the magnitudes worked. For each answer they chose the appropriate symbol with the help of the adult.

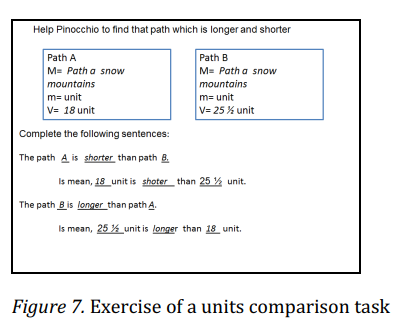
The Figure 7 shows an example of a paths comparison exercise in the perceptual stage. The children are given a sheet with two paths drawn and they are asked to measure them using a ribbon. Afterwards, the students write down the data obtained in a registry sheet and identify the measurement used, the shortest path, the longest path and their numeric representation.

Afterwards the students worked with a number of images that indicated the quantity of times a measurement was used. The goal of this exercise was to answer a variety of questions focused on the identification of the measurement and the semantic group, the comparison between objects (lesser than, greater than or equal), and the numeric representation of these comparisons. The figure 8 shows an example measuring the size of different birds and the questions used for this exercise.

The Figure 9 shows an example of liquids measurement using a magnitude of a water bottle. The measurement was a small cup used by the boy and wooden sticks were used to represent how many times the cup was used.

Subject 3. Teaching of ten (NS). The ten was introduced to children as a new unit of measurement. The children were taught that this new unit was obtained by adding up 10 units together and is placed on the left side of the units. Figure 10 show some example of tens localization.

Afterwards, children joined groups of ten matches together using a ribbon to tie them up, these groups of matches represented the tens and were used to build up other units of measurements (hundreds and thousands). The figure 11 shows an example of tens constructions and their localization on the positional value table.

After having finished the materialized stage the children were moved onto the perceptive stage. This stage goal is to identify the units of measurement used in a number of images and put them into groups. Figure 12 demonstrates an example.

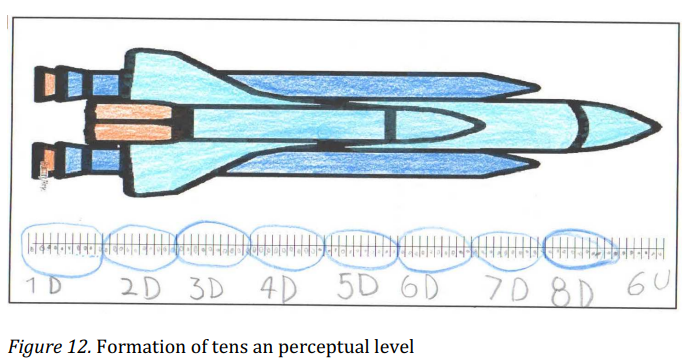
Figure 13 shows the data record used for the previous task and the questions they had to answer about the identified units.

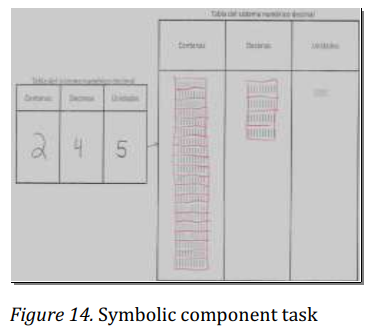
The next step was to teach children how to get a numeric representation based on groups of tens represented in a graphical way using the positional value table as shown in figure 14.

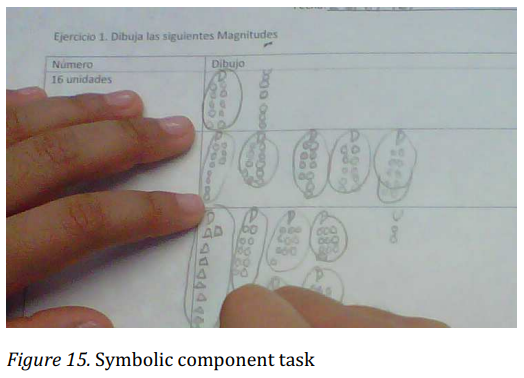
After children were able to identify the units of measurement out of a picture they were given the opposite task. They had to make a graphical representation of a number using the positional value table. Figure 15 shows an example.

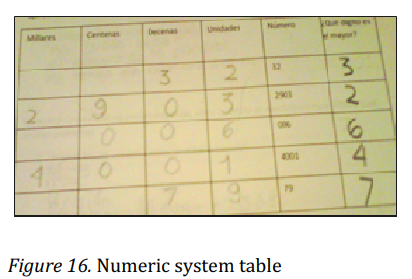
The final task consisted on the localization of different numbers using the numeric system table, and the identification of the biggest and the smallest digit on them. Figure 16 shows an example.

Results

Before and after implementing the program a qualitative analysis of the mathematical skills and components was performed. The initial evaluation demonstrated that children had not developed any general skills to assimilate the concept of decimal numeric system, actually, most of the tasks were almost impossible to be performer by the students unless they used back up material. In the final evaluation these problems were overcome by them, and they were able to finish all the tasks independently (only one student required perceptive support). Table 3 shows the evaluations results.

Table 3. Types of error in Pretest-Postest

The results obtained during the implementation of the teaching method are shown in Table 4, the number of exercise worked, the level of execution and types of errors. Only two mistakes were made and the beginning of the method.

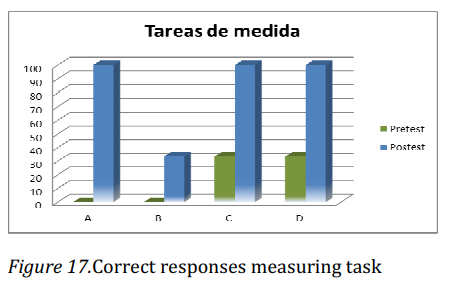
According to final results no systemic difficulties have taken place. Children solved most of the tasks independently. If children had any kind of difficulty, they asked for help immediately. The level of external assistance was verbal, in contrast to the initial assessment in which the level of external help was always at level of concrete actions. Three students (A, C, D) were able to perform tasks in the verbal and independent external level. The other student (B) required support in the perceptive stage (see figure 17).

Table 4. Tasks used in the teaching method

In table 5 the answer given by student (A) before and after the method application are shown.

Table 5. Measure task comparison