Диковинные задачи на уроках математики в школе и дома

От редакции: данная статья является основой для дискуссии, которая состоится на страницах этого номера журнала. Ее тема: «Как помочь родителям, детям и учителям нейтрализовать вред от некорректных учебных задач».

«Математический опыт учащегося нельзя считать полным, если он не имел случая решить задачу, изобретенную им самим»

(Д. Пойя).

В последние годы учебники математики стали усиленными темпами обогащаться странными и в то же время совсем не простыми задачами, извлеченными из многочисленных сборников по занимательной математике. При этом нередко совершенно сумбурно, алогично, вне связи с изучаемой темой. Более того, в строгую математику помещаются задачи, которые, мягко говоря, не относятся к математике. И вот ребенок с родителями битые часы, обзванивая близких друзей и родственников, погружаясь в интернет, пытаются узнать заветный ответ.

Первую задачу возьмем из учебника математики для начальной школы.

Два мальчика, Дима и Миша, отправились в булочную. По дороге они нашли 20 рублей. Сколько бы денег нашел Дима, если бы отправился в булочную один?

Очевидно, что при решении этой задачи не стоит долго мучиться, так как все ответы будут верные, даже если до денег Дима не дойдет, ничего не найдет или найдет аж 40 рублей! Ведь ситуация, когда Дима идет в булочную один, онтологически совершенно другая, чем когда они идут вдвоем. И здесь все может случиться. Смысл этой задачи состоит лишь в том, чтобы догадаться, что существуют не математические, а «бытовые» или в лучшем случае — софистические задачи. Удивляет, что подобные задачи в интернете вполне серьезно и подробно обсуждаются...

Вот другая задача.

Горело семь свечей, три потушили, сколько свечей осталось?

Данная задача имеет три противоречивых ответа. Первый ответ: четыре свечи, так как полноценными свечами считаются только те, которые горят. Второй ответ: семь свечей, так как все-таки все свечи остались. Третий ответ: три свечи, так как остальные, в конце концов, догорят и исчезнут. Вот такой вот курьез. Хорошо если составители задачников предупреждают, что подобные задачи необычные или шуточные.

Некоторые необычные задачи формулируют так, чтобы что-то существенное не договорить, а полагать существующим между строк. Например.

Половина — треть его.

Здесь задача построена на том, что вкладывается разный смысл в понятия половина и треть. В этой задаче «реципиента» наглым образом «разводят»... Половина — это не от «него». Половина — это всего лишь самодостаточное число 1/2, а треть — это доля от искомого числа. Тогда получается следующее уравнение: 1/2=х:3, очевидно, что результатом будет 1,5.

Рис. 1

Даем описание цветового наполнения каждой картинки, так как без этого невозможен правильный ответ: рыба — синий, черный, оранжевый, желтый; цыпленок — желтый, оранжевый, черный; поплавок — красный, черный, желтый, зеленый, белый, синий; собака — черный, белый, голубой, коричневый.

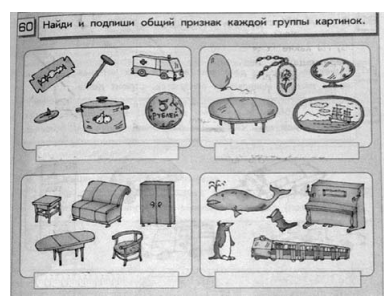
Рис. 2

Нередко задачи в режиме недоговоренности выглядят совсем уж двусмысленными. Вот подобная задача.

Требуется полсотни разделить на половину. Сколько получится?

Ответ: не 25, а 100! Объяснение: «на половину» — это не доля от целого, а просто число 1/2. Конечно, авторы задачи в этом случае сознательно совсем не стремились упростить задачу до следующего пассажа: требуется сотню разделить на два.

Нередко предлагаются задачи на смешение различных тем, на их неожиданное сопряжение. Например.

Сколько будет пять в квадрате, десять в квадрате? А чему равен угол в квадрате?

Эта задача математическая, но в ней сводятся воедино алгебраические (возвести число во вторую степень) и геометрические смыслы (мера угла в квадрате). На этом и построена вся фишка. И если субъект не готов к этому, то он запросто растеряется. Ответ: 25, 100, 90o.

Существуют так называемые эвристические задачи, в ходе решения которых возможны различные ходы мысли и ответы. Обычно в решении подобных задач проявляются неординарные классификации, напрямую зависящие от мироощущения и миропонимания субъекта, как например в задаче «Найти лишний предмет» (рис. 1).

На эту задачу даны были следующие ответы. Поплавок — единственный неодушевленный предмет. Цыпленок — только он сразу пойдет на дно, если его бросить в воду. Рыба — только она смотрит в левый верхний угол, а не в левый нижний. Собака — только в ее окраске полностью отсутствует желтый цвет. Как относиться к задаче и ответам на нее? Очевидно, что самым «вменяемым» является первый ответ, более- менее здравым — последний ответ. Остальные ответы — дело вкуса, юмора, фантазии и других «плохо скрываемых наклонностей» субъекта.

Кстати, здесь я вынужден признаться, что эта задача — не совсем «настоящая». Это задача-пародия, которую мне прислал коллега. Он хотел показать, как можно превратить простое задание в практически нерешаемое. А именно: сознательно заложить в него хитрость, которую другому человеку практически невозможно разгадать, так как это потребует от него самого натурального «разрыва шаблона»

Все приведенные выше ответы — неверные, поскольку неполные. А вот правильный звучит так: все предметы могут рассматриваться как лишние. Все зависит от того, какой очевидный признак выбран как основной.

С одной стороны — не поспоришь. Но с другой — ответ можно дать лишь в том случае, если догадаться, что автор решил просто поиздеваться над читателем. А это, согласитесь, мало кто сможет допустить, настолько подобное допущение «за гранью».

Впрочем, не спешите обвинять моего коллегу в предвзятости и «сгущении красок». Он всего лишь показал реальную абсурдную тенденцию. Как доказательство — вот задачка из той же серии, но из реального учебника (рис. 2). Общий признак первых трех «наборов» достаточно легко определяется: железные предметы, овальные предметы, мебель. Угадайте общий признак для набора картинок в правом нижнем углу. Правильный ответ: общий признак — отсутствие общего признака.

Важно отметить, что в последние годы детские задачки нередко проецируются и на взрослых. Ведь все понимают, что детские задачки решают не только дети, точнее — совсем не дети! Поэтому и проверяют на внимательность еще и взрослых, закладывая «схро­ны», чтобы и взрослые тоже «порезвились». Добавим, что вообще-то детский мир часто соседствует со взрослым, меняется с ним местами, порой их даже трудно разделить, например, дети любят взрослые шлягеры, а взрослые тети и дяди умиляются детским песенкам. Нечто подобное царит и в математике: дети охотно рассуждают о бесконечности, а взрослые стремятся преодолеть еще один барьер — решить очередную задачку из школьного учебника для начальной школы... Ведь учиться никогда не поздно!

Отчасти оправдаем тех, кто подбрасывает подобные задачки в сборники для детей: данные задачи могут быть нацелены на то, чтобы хоть как-то развеять «звериную серьезность», которую порой надевают на себя некоторые математики. Ведь не редкость, что когда с такими задачами встречаются сами математики, то они бывают в полной панике. Они привыкли к однозначности, а тут — «не пойми чего». Приведем в роли «лекарств» шуточные высказывания и притчи, связанные с математикой.

1.   Как-то ночью, когда Насреддин сладко спал, жена растолкала его и говорит:

— Ребенок целый час плачет, неужели ты не слышишь? Ведь он наполовину твой! Покачай его.

— Моя половина пусть плачет, — сказал Насред­дин. — Успокой свою половину.

С этими словами он повернулся к стене и заснул.

2.  «В школьной столовой».

Ученик: «Мне три вторых».

Повар: «А корень из минус двух не хочешь?!»

3.   Поучение: чем шире кругозор, тем тупее угол обозрения.

4.    У маленького математика спрашивают:

— Есть ли у крокодила крылья?

— Конечно! — уверенно отвечает он.

— Как так?! Откуда же у них крылья?!

— Просто их количество равно нулю.

Но настораживает ведь другое. Психологи считают, что с помощью знаний (тем более — «изощренных») можно легко терроризировать другого человека, ставить его в неприглядное положение. Ведь не случайно существует вполне обоснованное мнение, что знание не только сила, но и власть! А ведь учитель знает во много раз больше любого ученика! (Не дай Бог, чтобы педагог специально, в отместку подбрал подобные задачи для доказательства несостоятельности какого-либо ученика!) И не секрет, что учителя нередко пользуются этим — сознательно или бессознательно, прямо или завуалированно! Поэтому, как известно, учителей математики дети не только искренне любят, но и нередко ненавидят.

Приведем в пример еще одну задачу для первоклашек (рис. 3).

Это задача не такая простая, как кажется на первый взгляд. При ее анализе выясняется следующее: во-первых, цвета здесь, собственно, не принципиальны, они только отвлекают, во-вторых, карандаши и отрезки, их символизирующие, не обязательно должны быть равными, в-третьих, абстрагируясь от цветов и равенства карандашей и отрезков, можно прийти к выводу, что здесь важен лишь такой признак, как «равенство», то есть равные карандаши должны быть обозначены равными отрезками. Следовательно, нужно закрасить кружки с номерами 2 и 4.

Можно ли такую задачу давать без привязки к предшествующим «менее абстрактным» задачам, учитывая, что мышление ребенка этого возраста предельно конкретно?! Наверное, вопрос риторический. Вспомним лишь, сколько тысячелетий человечество шло к такому «простому» выводу, что падающее яблоко и Луну объединяет не только форма (приблизительно шарообразные), но и то, что они притягиваются Землей и находятся в режиме свободного падения. Наверное, имеет смысл для детей выделять задачи разной степени абстрактности: первый уровень, второй уровень и т. д.!

Итак, нужны ли необычные задачи в детских сборниках? Наверное, нужны. Но вот их польза, как гово
рится, амбивалентная.

Рис. 3

Ребенка бы строгой логике и последовательности мысли научить, дать почувствовать, что такое математика, а подобные задачи могут увести совершенно в другую «вероятностно-бытовую» сторону, где «веселый хаос — мать порядка». Поэтому многое зависит от методической подачи подобных задач учителем или родителем. Собственно, с помощью таких задач можно провести разграничительную линию между строгой математикой и околоматематическими сферами научного и полунаучного знания.

Продуктивны для развития критического мышления софистические примеры и задачи, в которых всегда запрятана ошибка. Например, нужно доказать, что дважды два пять. Доказываем.

4:4 = 5:5. Вынесем за скобки в каждой части его общий множитель. Получим: 4х(1:1) = 5х(1:1). Числа в скобках равны, поэтому 4=5, или 2х2=5. В чем ошибка?

Ошибка заключается в том, что распределительное свойство выглядит так: а(в±с) = ав±ас, то есть в скобках у нас сумма или разность, а не частное. Еще одна очень популярное софистическое умозаключение.

Полупустое есть то же, что и полуполное. Если равны половины, значит, равны и целые. Следовательно, пустое есть то же, что и полное.

Здесь в умозаключении обыгрывается уникальная ситуация, когда мы можем сказать, что полуполное есть то же самое, что и полупустое.

Нередко за такими задачами, даже для младших школьников, просиживает не один час «вся дружная семья». Весь интернет полон диалогов и советов, как решать ту или иную задачу. Одним словом, современные учебники не дают скучать даже седовласым дедушкам и бабушкам. С нескрываемым вздохом они, наверное, думают, что современные дети, судя по предлагаемым задачам, готовы продвинуться гораздо дальше их. Хотя дело, может быть, куда проще — сейчас наблюдается жесткая конкуренция не только у взрослых, но и у детей! Попробуйте попасть в современную гимназию, где классы набираются на конкурсной основе (хотя это тщательно скрывается)! Нетрудно заметить, что, судя по распределению средств на образование, нашему государству нужны скорее не добротные и добросовестные работники, а элита!

При этом редко кто сомневается в обоснованности введения тех или иных «эвристических задач». Совсем не обсуждается, что так постепенно не только детям, но взрослым прививается «чувство собственной неполноценности». Ведь порой не решаются задачи даже из начальной школы! Как ребенок в душе отреагирует, если даже Папа или Мама «детскую» задачу — вдруг — не одолеют?! А может, действительно наша педагогика, да и дети продвинулись так далеко, что за ними просто не угнаться?! Ну как в наш век «цифровых технологий» не решить задачки «от младших школьников» или даже «от дошкольников»!

Но нередко попадаются задачи, которые просто неточно сформулированы. Например, задачка из сборника для 2 класса очень известного автора.

Запишите число 6: а) тремя одинаковыми цифрами; б) двумя одинаковыми цифрами; в) шестью одинаковыми цифрами.

Очевидно, что число шесть записывается с помощью цифры 6, а, например, число шестнадцать — с помощью цифр 1 и 6. Но как записать данное число с помощью трех и даже шести одинаковых цифр? Может быть, в данной задаче имеется в виду, что записать нужно одинаковыми цифрами (скорее — числами) с использованием определенных знаков действий?! Но о них в формулировке задачи «ни гу-гу».

Да, есть в математике эвристические задачи. Но они остаются все же в рамках математики или интегрированных задач (на стыках различных предметов) и «уши у них не торчат». Другое дело, что их нужно в учебнике располагать таким образом, чтобы наблюдалась некая тенденция, эволюция, развитие, ну, в крайнем случае — прослеживались хоть чуть-чуть предсказуемые метаморфозы. Но без всякой связи, сами по себе эти задачи просто бессмысленно «зависают» и, конечно же, могут раздражать.

Вообще-то нравственно и психологически желательно, чтобы ребенок чувствовал, что он полностью освоил учебную страницу, параграф, учебник и «ничего не пропустил». Нерешенные задачи накапливаются «тяжким балластом», и маленького ребенка трудно порой успокоить фразами типа «эти задачи пока не для тебя, а для более продвинутых детей», «выбери задачи себе по силам», «не переживай, чуть позже к тебе это придет».

Популярны в учебниках задачи-шутки. Например.

Чтобы сварить 1 яйцо вкрутую необходимо 5 минут. Сколько времени потребуется, чтобы сварить вкрутую 3 яйца.

Вот еще одна подобная задача.

Двое играли в футбол 2 часа. Сколько времени играл каждый?

Обычно такие задачи детям нравятся, так как они достаточно быстро разгадывают, в чем «закавыка».

Сложнее доказать или обосновать необходимость подобных задач для развития ребенка. Вообще-то в этой области очень сложно найти нечто весомое, ведь даже так называемое «развивающее обучение», как выясняется только теперь, ничего существенного не открыло. Так что математическое развитие ребенка «тайна сия велика есть». Выяснить оправданность включения тех или иных задач можно только решая и изучая эти задачи комплексно.

Многие задачи даются на опережение программы. Например.

Если Вася купит одну конфетку, у него останется 1 руб., а на две конфеты ему не хватит 3 руб. Сколько стоит конфета?

Достаточно непривычная задача для ученика начальной школы, так как она легко решается с помощью системы уравнений. Младший же школьник будет ее решать с помощью прикидки. А вот другая более сложная подобная задача.

Два мальчика решили купить книгу. Одному не хватало 7 руб. Другому — 5 руб. Они сложили деньги, но все равно им не хватило 3 руб. Сколько стоила книга?

Нередко в учебник набирают задачи по комбинаторике и теории вероятностей, старинные задачи с архаичными понятиями, единицами измерения и т. п. при этом очень важно при решении необычных задач хотя бы примерно представлять себе, что же они развивают. Например, нижеприведенная задача развивает пространственное мышление.

Сколько равных треугольников можно составить из шести спичек?

Данная задача не решается на двумерной плоскости, но легко решается в трехмерном пространстве. Ответ: 4 (рис. 4).

Очень продуктивно использовать задачи, в которых мы как бы обнаруживаем противоречие со здравым смыслом. Например.

Цену товара повысили на 20%. Через некоторое время ее понизили на 20%. Что произошло с ценой товара?

Очень хочется сказать, что осталась прежней. Однако нужно помнить, что долю (проценты) мы всегда берем от целого. Оказывается, в задаче фигурируют два целых, две цены — большая и меньшая, относительно которых мы и находим 20%. А значит, 20% от большей цены будет больше 20% от меньшей цены. Следовательно, цена товара снизится.

Еще одна задача, которая, на первых взгляд, очень простая.

Автомобиль проехал расстояние между двумя городами со скоростью 60 км/ч и возвратился со скоростью 40 км/ч. Какова была средняя скорость его езды?

Очень хочется подсчитать устно: (60+40):2 = 50 км/ч. На самом деле получается 48 км/ч. Объяснение: в данной задаче отсутствует расстояние, заданной конкретным числом, но так как оно одинаковое, то его можно взять за единицу, тогда х=(1+1):(1/60+1/40)=48 км/ч. Полученная величина называется средним гармоническим.

Существуют задачи, которые обыгрывают здравый смысл человека. Например:

Рыба весит 4 кг плюс половина ее собственного веса. Сколько весит рыба?

Очень хочется сказать, что 4 кг+2 кг=6 кг. Но на самом деле ответ — 8 кг, так как 4 кг — это и есть половина от всей рыбы, то есть 4+1/2х=х. Подобная «интеллектуальная инерция» происходит и в том случае, когда ученик на «семью восемь» отвечает — «сорок восемь».

Самыми сложными являются парадоксальные задачи. Например, задача известная еще с античных времен.

Сможет ли быстроногий Ахилл догнать черепаху, если: он преодолевает разделяющее их расстояние, но и черепаха проползает еще немного, и так всякий раз до бесконечности.

Эту математическую задачу до сих пор еще никто однозначно не объяснил. Иногда ее объясняют с помощью понятия предела. Поэтому ребенок может здесь вполне пофантазировать и дать свое самобытное объяснение. Не погрешим против истины, если отметим, что формулировки классических задач кристаллизуются в течение веков. Попробуйте почитать и решить задачи из старых учебников, например, 18­19 веков!

Как же можно классифицировать необычные задачи?

1.   Нестандартные задачи — это задачи, которые редко встречаются в методических линиях решения типических задач и отличаются необычностью формулировок.

2.   Софистические задачи — это задачи, которые имеют «запрятанную», скрытую, неявную ошибку.

3. Избыточные задачи — это задачи, в которых есть лишние данные, призванные запутать обучающегося.

4.   Двусмысленные задачи — это задачи, в которых возможны несколько равноценных ответов.

5.   Эвристические задачи — это задачи, в которых возможны открытые ответы, предполагающие различные ходы мысли.

6.   Онтологические задачи — это задачи, в которых обнаруживаются различные уровни реальности, размерности, системы исчисления.

7.   Опережающие задачи — это задачи, которые подбираются и формулируются в зоне ближайшего развития учащегося.

8.    Ошибочные задачи — это задачи, в которых есть ошибки, поэтому они остаются на совести составителей учебника.

9.   Шуточные задачи — это задачи на понимание скрытого в них юмора.

10.   Парадоксальные задачи — это задачи, в которых могут быть два или несколько достоверных ответов.

Рис. 4

В заключение дадим некоторые советы. К любым необычным (под звездочкой) задачам в учебниках нужно относиться спокойно, ведь не они моделируют стратегическое развитие всех детей. Тем более, их эволюцию, как правило, авторы учебников серьезно не продумывают, а дают, так сказать, «для проверки на вшивость». Но если очень хочется научиться решать задачи повышенной сложности, то ребенку нужно пойти на математические кружки, где учитель продумывает тактику и стратегию, методику и методологию введения и усвоения подобных задач. Это очень нужно и для подготовки ребят к олимпиадам. Собственно, успешные педагоги свою индивидуальную технологию подготовки к олимпиадам, как правило, не раскрывают, это их «хлеб», «ноу-хау». Это, так сказать, только «для посвященных».

Вообще-то необычные задачи создаются «с нуля» нечасто, тем более их сейчас полным полно в интернете и различных сборниках. Собственно, такие задачи постепенно вызревали в истории математики и находили свое словесное выражение (меняются только числовые значения, обновляются «одежды» и сюжет, но суть остается). Таким образом, необычную задачу выдумать непросто, а если кто и пытается, то ему необходима не только серьезная математическая, но и филологическая и логическая подготовка.

Какие можно назвать базовые принципы по освоению и созданию задач?

1.   Задачи должны соответствовать возрасту детей и находиться в зоне их ближайшего развития.

2.   Задачи должны быть построены математически, логически и филологически грамотно.

3.   Задачи желательно давать не по одной, а блоком, комплексно, иерархически, по уровням, диффе­ренцированно, «от простого к сложному».

4.    Находить необычные задачи не «где попало», а в академических или презентабельных сборниках (многие, например, знают авторитетные замечательные сборники задач под редакцией Я.И. Перельмана, М.И. Сканави и др., которые много раз переиздавались и выверялись).

5.   Задачи, которые попадаются в наспех скомпонованных учебниках и сборниках, серьезно воспринимать не нужно, и относиться к ним стоит «философски». Авторитетные математические сборники, как правило, постоянно переиздаются.

И все-таки, как же создать, так сказать, «противоядие» от необычных задач, то есть научиться их понимать и решать?! Совет очень прост: нужно, во-первых, включать критическое мышление, а во-вторых, пробовать сочинять и решать задачки самим. И, в конце концов, понять, что «не боги горшки обжигают», то есть задачки сочиняют люди, а они могут ошибаться или формулировать условие задачи не совсем корректно. В этой связи в контексте школьного образования вполне современно звучит мысль математика Д. Пойя о том, что «Математический опыт учащегося нельзя считать полным, если он не имел случая решить задачу, изобретенную им самим».