Уверенность в решении: моделирование и экспериментальная проверка

В работе анализируется процесс выполнения наблюдателем сенсорных задач. Кратко представлено описание разработанной с позиции теории обнаружения сигнала (ТОС) модели принятия решения с оценкой уверенности в его правильности. В парадигму ТОС введено понятие уверенности идеального наблюдателя. Для реального наблюдателя обоснован подход к измерению уверенности через сумму эвристических свидетельств. Показано, что вероятность правильности уверенных ответов превышает вероятность правильности всех (уверенных и неуверенных) ответов. В экспериментальном исследовании выполнения двух видов пороговых задач на материале зрительного различения пространственных признаков стимулов (размеров окружностей) и временных (длительностей световых сигналов) это предсказание модели подтвердилось. Пилотажное диагностическое исследование позволило высказать гипотезу, что контроль за правильностью сенсорных решений с помощью переживаний уверенности–сомнений у рефлективных лиц выше, чем у импульсивных.

Введение

Настоящая работа продолжает исследования уверенности при решении сенсорных задач, результаты которых были представлены ранее (Шендяпин, 2007, 2010; Шендяпин, Барабанщиков, 2008; Шендяпин, Скотникова, 2003, 2006; Шендяпин и др., 2008, 2010). Целью данных исследований является теоретическая разработка и экспериментальная проверка математической модели процесса решения сенсорной задачи порогового различения близких по величине признаков объектов с наиболее детальным описанием важнейшей подсистемы этого процесса – принятия решения, включающего оценку уверенности в его правильности. Рассматривается базовый аспект уверенности в суждениях, отражающий такую важную внешне регистрируемую ее характеристику, как вероятность правильности решений.

Очевидна актуальность изучения принятия решения как базового звена выполнения любой когнитивной задачи. Последовательная реализация принципа системности в психологии способствует развитию исследований интегративных психических образований, структур, механизмов и функциональных систем (Барабанщиков, 2005), к которым в настоящее время относят и процессы принятия решения (Карпов, 2003). Одним из направлений таких исследований является разработка моделей психических процессов, достаточно интенсивно развивавшаяся в отечественной науке в 70–80-х годах XX века, однако позже ушедшая на второй план. Преодоление такого рода упущений в различных областях психологического знания приобретает особое значение для современной науки. И здесь немаловажную роль играет разработка методического материала, системных методов и средств анализа психических процессов, одним из которых является, с нашей точки зрения, метод математического моделирования; кроме того, его разработка имеет также практическое значение для превращения технологии научно-исследовательской деятельности в технологию организации жизненной сферы человека (Барабанщиков, 2005).

Исследования в рамках теории принятия решения достаточно активно развиваются за рубежом начиная с середины ХХ века; позже к ним добавилось также изучение уверенности в принятом решении (в частности, на материале сенсорно-перцептивных задач порогового типа), в результате чего были разработаны математические модели принятия решения и оценки уверенности в нем (Balakrishnan, Ratcliff, 1996; Bjorkman et al., 1993; Ferrel, McGoey, 1980, Ferrel, 1995; Heath, 1984; Heath, Fulham, 1988; Lacouture, Marley, 2000; Link, Heath, 1975; Link, 2003; Usher, Zakay, 1993; Usher, McClelland, 2001; Van Zandt, Maldonado-Molina, 2000; Vickers, Lee, 1998, 2000; Vickers, 2003 и др.).

Однако проведенный анализ предлагаемых моделей уверенности выявил следующие проблемы:

1. Несмотря на то, что все эти модели признают уверенность случайной величиной, значения которой при измерениях меняются от пробы к пробе, между ними не существует единства в оценке этой величины. Так, модели ряда авторов (Balakrishnan, Ratcliff, 1996; Bjorkman et al., 1993; Ferrel, McGoey, 1980; Ferrel, 1995), базирующиеся на теории обнаружения сигнала (ТОС) (Иган, 1983; Green, Swets, 1974), задают величину уверенности в правильности ответа как расстояние на оси значений сенсорного впечатления от точки полученного в данный момент впечатления до точки принятия решения. В моделях случайных блужданий (Heath et al., 1984, 1988; Link et al., 1975, 2003) и аккумуляторной (Vickers, Lee, 1998, 2000; Vickers, 2003) уверенность определяется через специально введенные величины свидетельств, связанные с сенсорными впечатлениями. Таким образом, названные модели признают связь уверенности с величиной сенсорного впечатления, полученного наблюдателем в данной пробе, однако несогласованность в вопросе определения величины уверенности, а также отсутствие ответа на вопрос, какое же из двух определений предпочтительнее для объяснения феномена уверенности, являются, на наш взгляд, серьезной проблемой в исследованиях данного феномена.
2. Еще одним недостатком данных моделей является отсутствие анализа связи величины уверенности в правильности принимаемого наблюдателем в данной пробе решения с величиной условной вероятности его правильности. Между тем в ТОС давно доказано, что условная вероятность правильности принятого решения (обозначаемая как апостериорная вероятность присутствия сигнала) зависит от отношения правдоподобия, соответствующего конкретному значению сенсорного впечатления. Поскольку вышеуказанные модели признают, что уверенность тоже зависит от величины сенсорного впечатления, то тем самым они признают, что связь величины уверенности с величиной условной вероятности правильности существует. Однако конкретный вид этой связи пока не установлен. Таким образом, остаются без ответа важные исследовательские вопросы: может ли наблюдатель, контролируя уровень своей уверенности, влиять на правильность принимаемых решений, и если это влияние возможно, то как должно быть изменено обоснованное в ТОС описание механизма принятия решения, не учитывающего влияние уверенности на правильность решения.

Для преодоления подобных проблем и поиска ответов на поставленные вопросы мы использовали строгий формальный подход к моделированию уверенности, опирающийся на аппарат ТОС, что позволило установить ранее не проясненную аналитическую связь между уверенностью идеального наблюдателя и вероятностью правильности принимаемых им решений. Полученные результаты способствовали получению ясно обоснованных эвристик для измерения уверенности реального наблюдателя.

При решении сенсорных задач испытуемого часто просят оценить уверенность в своем ответе с помощью конечного набора дискретных значений субъективной вероятности правильности вынесенного им ответа (Adams, 1957). Тем самым, с одной стороны, в психофизике фактически признается связь уверенности с вероятностью правильности в виде монотонной зависимости одной величины от другой, однако, с другой стороны, в психологических исследованиях принятия решения было не раз показано, что для человека нетипично математическое вычисление вероятности достижения цели.

В результате многочисленных исследований был сделан вывод о том, что, принимая решения в условиях неопределенности, человек на самом деле использует эвристические способы, которые сводят сложные задачи оценки субъективных вероятностей к более простым и интуитивно понятным операциям суждения (Тверски, Канеман, 2005), чему можно найти лишь одно объяснение – вычислительные возможности человека крайне ограниченны. Таким образом, применительно к нашей задаче для разработки новой модели уверенности необходимо найти простой эвристический механизм оценки вероятности, основанный на суждениях о сенсорных впечатлениях, получаемых от предъявляемых стимулов.

Для этого вначале нами была разработана идеальная модель принятия решения и оценки вероятности его правильности (Шендяпин, Барабанщиков, 2008; Шендяпин и др., 2008), которая описывает поведение рационального наблюдателя. Модели такого типа в математической психологии принято называть нормативными, так как в них отображается не то, что происходит на самом деле во время разворачивания некоего процесса, а скорее то, что прогностически должно было бы происходить в том случае, если справедливы некоторые исходные гипотезы (Ломов, 1981). Нормативная модель принятия решения, не учитывающая уверенность, известна в рамках ТОС давно (см., например, Иган, 1983). Однако наша нормативная модель, кроме правила принятия решения, содержит также аналитическую формулу для получения вероятности правильности принятого решения, что и составляет новизну данного психофизического исследования.

Идея нашего подхода состояла в том, чтобы, используя аппарат ТОС и гипотезу о монотонной зависимости вероятности правильности от уверенности, аналитическим путем найти формальную переменную ТОС, которая удовлетворяет этому априорно заданному свойству уверенности; найденную переменную можно было бы принять за рационально обоснованную модель уверенности.

В процессе поиска математического выражения зависимости вероятности правильного обнаружения сигнала от параметров задачи мы обнаружили, что такой переменной является натуральный логарифм произведения отношения априорных вероятностей предъявляемых стимулов на отношение правдоподобия, зависящее от сенсорного впечатления. Увеличение этой переменной вызывает монотонный рост вероятности правильности принятого решения. Найденную переменную мы назвали уверенностью идеального наблюдателя, так как именно данная переменная, вернее, знание ее величины позволяет идеальному наблюдателю вычислять вероятность обнаружения сигнала. Идеальность наблюдателя выражается в том, что он имеет все необходимые знания и вычислительные ресурсы для решения своей задачи: он может точно вычислять и уверенность, и зависящую от нее вероятность правильности. Так как принятие рациональных решений целиком основано на знании вероятности правильности принимаемого решения, то для идеального наблюдателя уверенность не имеет исключительного значения, она является всего лишь одной из промежуточных переменных, необходимых ему для вычисления вероятности.

У реального же наблюдателя таких ресурсов для выполнения сложных вычислений не существует, и он вынужден оценивать величину вероятности, имея только приближенное, полученное эвристическим путем, значение реально существующей уверенности, основанное на сенсорных впечатлениях. Поэтому уверенность является для него исключительно важным инструментом, с помощью которого он в конечном итоге и принимает решение.

Конечно, нормативная модель отражает только объективные стороны решаемой задачи и не учитывает всей специфики реализации результатов, полученных конкретным человеком. Теоретическое значение нашей модели идеального наблюдателя, полученной с помощью ТОС, состоит не только в объяснении того, как рациональный наблюдатель должен реализовывать процесс решения сенсорных задач, но и в ответе на интересующий нас вопрос: от какой переменной зависит вероятность правильности принятого решения в конкретной пробе?

Практическое значение нормативной модели состоит в том, что она гарантирует существование и дает описание точного метода вычисления величины уверенности идеального наблюдателя, повышение которой приводит к монотонному росту вероятности правильности решения, принятого в конкретной экспериментальной пробе. Наличие же точного метода позволяет искать обоснованные эвристики для упрощения вычислений. Заметим лишь, что проведенный затем анализ возможностей упрощения идеальной модели действительно позволил получить эвристический способ нахождения оценки уверенности, обеспечивающий разумную близость деятельности человека к идеальному результату (Шендяпин, Барабанщиков, 2008).

В настоящей работе проверялась гипотеза об уверенности как факторе, напрямую связанном с правильностью решений, которая была подтверждена как в рамках полученной в парадигме ТОС теоретической зависимости вероятности правильности уверенных решений от ширины зоны сомнений на оси принятия решения, так и в ходе экспериментальной проверки на материале выполнения сенсорных задач «больше–меньше» и «одинаковые– разные».

Идеальная модель принятия решения и оценки вероятности его правильности

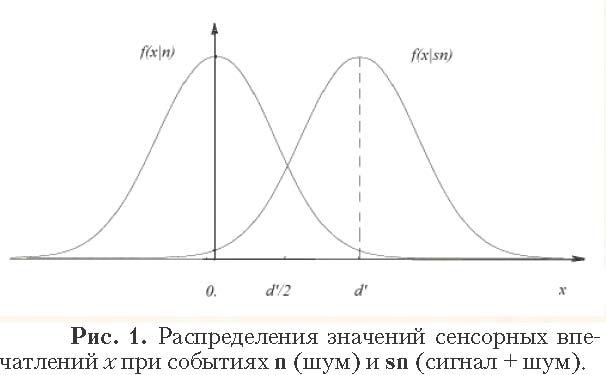
Неопределенность. Неопределенность в сенсорной задаче различения заключается в том, что наблюдателю достоверно не известно, какой из двух возможных стимулов он наблюдает. При различении двух близких по величине стимулов предъявление того из них, который порождает на выходе сенсорной системы наблюдателя меньшее по среднему значению впечатление, называется событием n (noise, т.е. шум). А предъявление другого стимула, порождающего на выходе сенсорной системы большее среднее впечатление, называется событием sn (signal + noise, т.е. сигнал + шум). Так как к среднему, т.е. детерминированному, отклику сенсорной системы на предъявляемый стимул всегда добавляется внутренний шум самой системы, то любая величина реакции сенсорной системы x может быть вызвана как событием n, так и событием sn.

Априорные вероятности. В ТОС предполагается, что наблюдателю известна априорная вероятность появления события sn, равная P(sn). Априорная вероятность появления дополнительного к нему события n при этом равна P(n) = 1 – P(sn). Отношение априорных вероятностей: l0 = P(sn)/P(n) (1) показывает, насколько событие sn появляется чаще или реже, чем событие n. Величина l0 в концентрированном виде выражает ту информацию, которой наблюдатель обладает еще до самого наблюдения. Если l0 > 1, то наблюдателю следует прогнозировать, что скорее всего будет событие sn, а не событие n. И чем больше логарифм отношения априорных вероятностей ln(l0), тем больше должна быть его уверенность в этом прогнозе. Если же l0 < 1, то скорее всего будет событие n. И чем больше логарифм обратного отношения априорных вероятностей ln(1/l0), тем больше должна быть уверенность в этом прогнозе.

Наблюдение. Описание сенсорного впечатления человека при наблюдаемых событиях задается в ТОС в виде случайной величины X, принимающей значения x, распределенные по закону f(x|n) при событии n, либо по закону f(x|sn) при событии sn (рис. 1).

Величина отношения правдоподобия для конкретного значения x, равная отношению плотностей вероятностей l(x)= f(x|sn)/f(x|n), показывает, насколько чаще данное значение сенсорного впечатления x появляется при событии sn, чем при событии n.
Апостериорные вероятности. Апостериорной вероятностью P(sn|x) в ТОС называют вероятность события sn при условии, что на выходе сенсорной системы было получено значение сенсорного впечатления x. P(n|x) = 1 – P(sn|x) – апостериорная вероятность дополнительного к нему события n. Апостериорные вероятности событий можно выразить через известные априорные вероятности и полученное в результате наблюдения отношение правдоподобия.

Обозначим через g(sn,x) функцию плотности вероятности совпадения двух событий: а) попадания полученного значения x в элементарный интервал dx и б) реализации события sn. Используя формулу для вероятности совпадения этих событий, получаем, что:
g(sn,x) dx = P(sn) f(x|sn) dx = f(x) dx P(sn|x). (2) При этом f(x) = P(sn) f(x|sn) + P(n) f(x|n) = P(sn) f(x|sn) {1 + [l(x) l0] –1}. Отсюда получаем апостериорные вероятности:
P(sn) f(x|sn) P(sn) f(x|sn) l(x) l0 l(x) l0 P(sn|x) = ---------------= ----------------------------- = ------------- , (3) f(x) P(sn) f(x|sn)[1+l(x)l0] 1 + l(x) l0 1 P(n|x) = 1 – P(sn|x) = -------------- . (4) 1 + l(x) l0 В дальнейшем нам будет также удобно использовать отношение апостериорных вероятностей: c(x) = P(sn|x)/P(n|x) = P(sn|x)/(1 – P(sn|x)) = l(x) l0 . (5) Введенное отношение апостериорных вероятностей оказалось равным произведению отношения априорных вероятностей и отношения правдоподобия. Заменяя в (3) l(x) l0 на c(x), получаем, что апостериорную вероятность P(sn|x) можно выразить через отношение апостериорных вероятностей c(x): P(sn|x) = c(x)/[1 + c(x)]. (6) Выражения (5) и (6) показывают, как с рациональной точки зрения следует действовать наблюдателю для вычисления вероятности присутствия сигнала P(sn|x) в данной пробе. После завершения наблюдения физического стимула и получения величины сенсорного впечатления x он должен действовать по следующему алгоритму: а) вычислить отношение правдоподобия l(x) = f(x|sn)/f(x|n), б) по формуле (5) вычислить отношение апостериорных вероятностей c(x) = l(x) l0, в) по формуле (6) вычислить P(sn|x) – апостериорную вероятность события sn, г) вычислить P(n|x) – апостериорную вероятность дополнительного события n. Таким образом, полученная информация позволяет идеальному наблюдателю принять рационально обоснованное решение, конечно, реальный наблюдатель такие сложные вычисления не проводит, что будет показано ниже.

Если от отношений l0, l(x) и c(x) перейти к их натуральным логарифмам: L0 = ln(l0), L(x) = ln[l(x)] и C(x) = ln[c(x)], то вместо формул (4), (5) и (6) можно получить более наглядные и удобные для анализа выражения:
C(x) = L(x)+ L0 , (7) P(sn|x) = exp[C(x)] {1+exp[C(x)]}–1 = 0,5 + 0,5 th{[C(x)]/2}, (8) P(n|x) = 0,5 – 0,5 th{[C(x)]/2}. (9) Формула для определения зависимости P(sn|x) и P(n|x) от C(x) в виде гиперболического тангенса получена в рамках парадигмы ТОС впервые. Графики зависимостей P(sn|x) и P(n|x) от C(x), рассчитанные по формулам (8) и (9), показаны на рис. 2. Видно, что с ростом C(x) вероятность P(sn|x) монотонно растет от 0 до 1, а P(n|x) монотонно убывает от 1 до 0. При значении x, удовлетворяющем условию L(x) = -L0, C(x)= = 0, вероятности событий sn и n совпадают и равны 0,5. При значении x, удовлетворяющем условию L(x) = 0, отношение правдоподобия равно 1: l(x) = 1. Подставляя l(x) = 1 в формулы (3) и (4), получаем P(sn|x) = P(sn) и P(n|x) = =P(n), т.е. апостериорные вероятности событий при этом равны априорным.
Принятие решения. Принятие решения начинается после наблюдения и внешне выглядит как оценка истинности утверждения «данное значение x было вызвано событием sn». Если наблюдатель согласен с этим утверждением, то должен сказать «да». Если же он скорее не согласен, то должен сказать «нет». Решение в виде ответа «да» является событием Y (yes – да), а решение в виде ответа «нет» – событием N (no – нет).

Ситуация после получения значения x описывается двумя несовместными сочетаниями событий: (sn|x) и (n|x). После принятия решения и появления события Y или N ситуация описывается уже четырьмя несовместными сочетаниями: (sn,Y|x), (sn,N|x), (n,Y|x) и (n,N|x). Несовместность сочетаний событий означает, что в каждой пробе при данном значении x реализуется только одно из четырех возможных совпадений. Решающее правило для вынесения ответа разбивает X – множество всех получаемых в результате наблюдения значений x – на три непересекающихся подмножества: XY, XN и X0. При x, принадлежащих XY, выносится ответ Y. Таким образом, на подмножестве XY может возникнуть только одно из двух совпадений: (sn,Y|x) или (n,Y|x). При x, принадлежащих XN, выносится ответ N. Соответственно на XN может возникнуть только одно из двух совпадений: (sn,N|x) или (n,N|x). При x, принадлежащих X0, невозможно дать однозначный ответ.

Поскольку в каждой пробе сенсорное впечатление х может быть результатом как события sn, так и события n, то решающее правило для вынесения ответа зависит только от x и не зависит от имевшего место события sn или n, т.е. при вынесении ответа информация о событии не используется. При этом в соответствии с теоремой вероятности совпадения двух независимых событий вероятность совпадения события sn и ответа Y при данном x равна:
P(sn,Y|x) = P(sn|x) P(Y|x),
где P(Y|x) – условная вероятность ответа Y при данном x.

В силу детерминированности решающего правила условная вероятность P(Y|x) принимает на всем множестве X только два возможных значения: 0 и 1. Фактически P(Y|x) играет роль функции принадлежности для подмножества XY: для x, принадлежащих XY, она равна 1, а на подмножествах XN и X0 она обращается в нуль. Тогда
P(n,N|x) = P(n|x) P(N|x),
где P(N|x) – функция принадлежности x к XN, которая обращается в 0 на XY и X0.

Аналогично:
P(n,Y|x) = P(n|x) P(Y|x) и P(sn,N|x) = P(sn|x) P(N|x).

Сочетание (sn,Y|x) называется правильным обнаружением сигнала (события sn) при данном значении x. Сочетание (n,Y|x) – ложной тревогой (ошибочным обнаружением события sn). Сочетание (sn,N|x) – пропуском сигнала (ошибочным обнаружением события n). Сочетание (n,N|x) – правильным отрицанием (правильным обнаружением события n). Сумма безусловных вероятностей всех возможных сочетаний событий и решений равна 1: P(sn,Y) + P(n,Y) + P(sn,N) + P(n,N) = 1.
При этом безусловная вероятность получения правильных решений P(Cor) (correct – правильный) независимо от того, при каком x они были получены и каким было само решение, задается суммой:
P(Cor) = P(sn,Y) + P(n,N) = ∫P(sn,Y|x) f(x)dx + ∫P(n,N|x) f(x)dx = XX
Y N = ∫P(sn|x) f(x)dx + ∫P(n|x) f(x)dx. (10) XY XN
Величина P(Cor) зависит от того, как наблюдатель разобьет X на XY и XN своим решающим правилом. Из рис. 2 и формул (8), (9) видно, что в принципе при любом значении x можно принять как решение Y (вероятность его правильности будет равна P(sn|x) > 0), так и решение N (вероятность его правильности равна P(n|x) > 0). Однако если наблюдатель хочет получить максимум вероятности правильных решений P(Cor), то в каждой пробе из двух возможных при данном значении x альтернатив ответа он должен выбирать ту, которая приносит ему большую вероятность правильности ответа. Поэтому если при данном значении x выполняется неравенство P(sn|x) > P(n|x), то он должен выбрать решение Y, так как тогда он получит вероятность правильности P(sn,Y|x) бóльшую, чем вероятность правильности альтернативного решения P(n,N|x). А если P(sn|x) < P(n|x), то он должен выбрать решение N, так как тогда он получит P(sn,Y|x) < P(n,N|x).

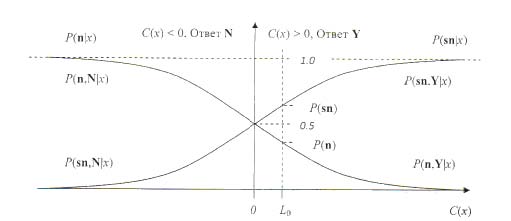
Рис. 2. Зависимости апостериорных вероятностей P(sn|x) и P(n|x) от C(x). При C(x) = L0 апостериорные вероятности совпадают с априорными. Решающее правило полученной идеальной модели ТОС: при C(x) > 0 принимается решение Y, иначе принимается решение N. P(sn,Y|x) и P(n,N|x) — вероятности правильности принятых решений. P(n,Y|x) и P(sn,N|x) — вероятности ошибочности принятых решений

Так как в соответствии с рис. 2 неравенство P(sn|x) > P(n|x) эквивалентно неравенству C(x) > 0, а неравенство P(sn|x) < P(n|x) эквивалентно неравенству C(x) < 0, то решающее правило идеальной модели ТОС можно сформулировать следующим образом: если x принадлежит XY ={C(x) > 0}, то принимается решение Y, если x принадлежит XN = {C(x) < 0}, то принимается решение N. При этом в соответствии с найденными нами формулами (8) и (9) вероятности правильности принятых решений Y и N вычисляются следующим образом:
P(sn,Y|x) = 0,5 + 0,5 th{[C(x)]/2}, при C(x) > 0, (11)
P(n,N|x) = 0,5 – 0,5 th{[C(x)]/2}, при C(x) < 0. (12)

А вероятности ошибочности принятых решений Y и N вычисляются по формулам:
P(n,Y|x) = 0,5 – 0,5 th{[C(x)]/2}, при C(x) > 0, (13)
P(sn,N|x) = 0,5 + 0,5 th{[ C(x)]/2}, при C(x) < 0. (14)

При x, принадлежащем X0 = {C(x) = 0}, невозможно сделать однозначный выбор решения, так как вероятности правильности обоих ответов одинаковы и равны 0,5.

Отметим, что полученное решающее правило конкретизировало определение подмножеств XY, XN и X0: XY содержит все x, удовлетворяющие неравенству C(x) > 0, аналогично XN = {C(x) < 0}, а X0 = {C(x) = 0} содержит решения уравнения C(x) = 0.

Уверенность в правильности принятого решения. Мы получили, что в идеальной модели ТОС имеется переменная C(x) = L(x)+ L0, позволяющая при данном значении x принимать решение и по формулам (11), (12) оценивать вероятность его правильности. Именно таким свойством (быть инструментом для оценки вероятности правильности), как мы предполагали, обладает психологическая уверенность человека в правильности принятого решения. Напомним, что по своему формальному определению величина C(x) равна натуральному логарифму отношения P(sn|x)/P(n|x). Если переменная C(x) = 0, то ни одно из альтернативных решений не имеет преимущества, так как вероятности их правильности одинаковы и равны 0,5.

Естественно считать, что человек, находясь в такой ситуации, полностью не уверен в своем выборе, т.е. его субъективная уверенность равна 0.

Если C(x) > 0, т.е. P(sn|x) > P(n|x), то, согласно решающему правилу идеальной модели, принимается решение Y. Так как вероятность его правильности P(sn,Y|x) превышает вероятность его ошибочности P(n,Y|x), то субъективная уверенность человека в правильности принятого решения Y должна быть положительной величиной. Причем чем больше C(x), тем значительнее P(sn,Y|x) превышает P(n,Y|x) и, следовательно, тем большей должна быть величина субъективной уверенности человека в правильности принятого решения.

Если же C(x) < 0, то принимается решение N, и вероятность его правильности P(n,N|x) превышает вероятность его ошибочности. И опять, чем больше абсолютная величина C(x), тем значительнее превышение вероятности правильности решения над вероятностью его ошибочности и тем увереннее должен быть человек в правильности принятого решения.
Как мы убедились, величина C(x) психологически точно описывает уверенность человека, принимающего рациональные решения. Поэтому ее совершенно обоснованно можно назвать уверенностью идеального наблюдателя.

Эвристическая модель принятия решения и оценки уверенности в его правильности

Полученная идеальная модель ТОС является универсальной, что позволяет использовать ее результаты для принятия решения и вычисления вероятности его правильности с помощью любых устройств, способных измерять значения x и обладающих необходимыми вычислительными средствами для вычисления логарифма отношения апостериорных вероятностей. Такими устройствами могут быть как объекты неживой природы (например, технические автоматы), так и живые существа.

Однако можно ли использовать полученную в ТОС уверенность идеального наблюдателя C(x) = L(x)+ L0 для моделирования поведения реального человека? Как уже отмечалось, многие психологи, занимающиеся проблемой принятия решений, согласны в том, что люди в реальной жизни редко используют математический аппарат теории вероятности. Такие авторитетные исследователи, как А. Тверски и Д. Канеман, считают, что при принятии решений в условиях неопределенности «люди полагаются на ограниченное число эвристических принципов, которые сводят сложные задачи оценки вероятностей и прогнозирования значений величин к более простым операциям суждения» (Тверски и Канеман, 2005, с. 17).

Еще один известный специалист в области теории принятия решений Ю. Козелецкий также считает, что «использование, даже упрощенное, правил теории вероятностей затруднительно и часто требует применения больших мыслительных усилий, перегружая кратковременную и долговременную память» (Козелецкий, 1979, с. 161). Соглашаясь с тем, что «эвристические принципы действительно не позволяют оценивать вероятности событий с такой же точностью, как это позволяет делать теория вероятностей», Козелецкий объясняет факт широкого использования приближенных эвристик тем, что «они, как правило, достаточно легки для интуитивного понимания и использования» (там же).

В связи с такими выводами экспертов в области принятия решений возникает вопрос: нельзя ли как-то упростить процесс вычисления логарифма отношения правдоподобия L(x) и свести его к простым вычислительным эвристикам, более свойственным людям? Анализ этой проблемы показал, что возможности упростить процесс вычисления L(x) действительно имеются.

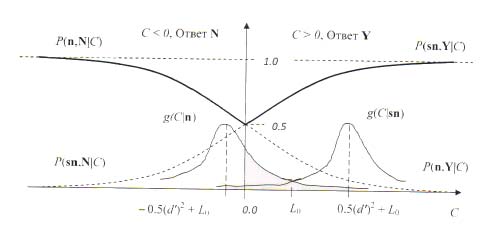
Рис. 3. Зависимости вероятностей правильности решений P(sn,Y|C), P(n,N|C) и вероятностей ошибочности решений P(n,Y|C), P(sn,N|C) от суммы свидетельств C. Решающее правило эвристической модели: при C > 0 принимается решение Y, иначе принимается решение N. g(C|sn) и g(C|n) – нормальные законы распределения случайной величины C при событиях sn и n

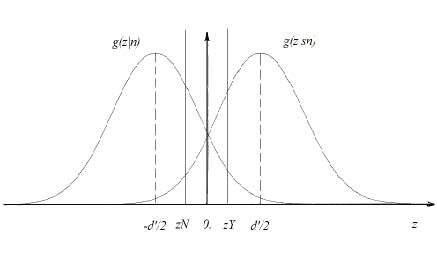
Рис. 4. Законы распределения g(u|sn) и g(u|n) нор- мированной переменной u = C/d’ для равновероятных событий sn и n

Нормальное приближение для сенсорного впечатления. Если условные плотности распределений вероятностей f(x|sn) и f(x|n) близки к нормальным и у них примерно одинаковые дисперсии, то при условии, что среднее впечатление от события n совпадает с нулем (см. рис.1), выражение для отношения правдоподобия сильно упрощается (Иган, 1983):
l(x) = f(x|sn)/f(x|n) = exp[d’ (x – d’/2)] , (15)
где d’ – различимость этих равновариативных нормальных распределений, а x – сенсорное впечатление, нормированное на их среднее квадратическое отклонение. Натуральный логарифм отношения правдоподобия при этом может быть приближенно вычислен по очень простой формуле:
L(x) ≈ d’ (x – d’/2), (16)
которая вполне соответствует функциональным возможностям мозга человека.

Эвристическая модель уверенности. Окончательно переходя от идеальной модели ТОС к разрабатываемой нами эвристической модели принятия решения, получаем, что при условии справедливости нормального приближения не идеальный наблюдатель, обладающий очень ограниченными вычислительными возможностями (например, умеющий выполнять только арифметические операции), может использовать для вычисления уверенности C(x) простую эвристическую формулу в виде суммы:
C(x) ≈ d’ (x – d’/2) + L0. (17)

Соотношение с аккумуляторной моделью. Первое слагаемое суммы (17) по смыслу можно соотнести со свидетельствами в пользу сравниваемых альтернатив решения, введенными Д. Викерсом (Vickers, Lee, 1998) в его аккумуляторной модели принятия сенсорных решений с оценкой уверенности, являющейся в настоящее время одной из наиболее авторитетных за рубежом (см. об этом: Шендяпин и др., 2008). Поэтому вслед за Викерсом будем называть полученную нами переменную e = d’ (x – d’/2) сенсорным свидетельством. Различие же между ними состоит в том, что у свидетельств, введенных Викерсом, нет множителя d’. При этом смысл величины свидетельства в обоих случаях вполне понятен: если e = d’ (x – d’/2) > 0, то значение e действительно можно считать равным весу свидетельства в пользу события sn, а если e = d’ (x – d’/2) < 0, то это может свидетельствовать скорее в пользу события n, чем в пользу sn (см. рис. 1). И чем больше абсолютная величина свидетельства, тем более обоснован выбор в ответе соответствующего события.

Множитель d’ в данном случае играет роль детерминированного сомножителя сенсорного свидетельства, а (x – d’/2) – его случайного сомножителя. Таким образом, на величину сенсорного свидетельства, на основе которого рациональный наблюдатель с ограниченными вычислительными возможностями принимает решение, влияют два фактора: отклонение сенсорного впечатления x от порога d’/2 и различимость предъявляемых стимулов d’.

Необходимо отметить, что замена уверенности идеального наблюдателя на свидетельства в пользу рассматриваемых альтернатив решения является очень плодотворной: так как на процесс принятия решения и на величину вероятности правильности принятого решения влияет именно сумма e + L0, то L0 также можно рассматривать как свидетельство. Только в отличие от апостериорного сенсорного свидетельства e его следует считать априорным свидетельством. При L0 > 0 априорное свидетельство эквивалентно приращению положительного сенсорного свидетельства, а при L0 < 0 оно эквивалентно приращению отрицательного сенсорного свидетельства.

Поэтому в отличие от идеальной модели, где уверенность C(x) выступает просто как формальная переменная, не имеющая очевидного практического смысла, в эвристической модели уверенность можно рассматривать как сумму интуитивно хорошо понимаемых свидетельств (величина которых линейно зависит от величины сенсорного впечатления) в пользу рассматриваемых альтернатив ответа.

Математическая эквивалентность переменных x и C, вытекающая из соотношения (17), позволяет получить характеристики и закон распределения случайной величины C. Так как первое слагаемое переменной C распределено по нормальному закону, а второе является константой, то и сама переменная C также распределена по нормальному закону (см. графики нормальных распределений g(C|sn) и g(C|n) на рис. 3). Среднее значение сенсорного свидетельства e = d’(x – d’/2) в случае события sn равно + 0,5(d’)2, а в случае события n равно – 0,5(d’)2. Соответственно, среднее значение C равно + 0,5(d’)2 + L0 при событии sn, а при событии n оно равно – 0,5(d’)2 + L0. Дисперсии величин C в обоих случаях равны (d’)2.

Таким образом, различимость распределений g(C|sn) и g(C|n) так же, как и для f(x|sn) и f(x|n), равна d’. Это известное свойство нормальных распределений: распределения логарифма отношения правдоподобия для нормальных распределений с одинаковыми дисперсиями являются также нормальными и имеют такую же различимость, как и исходные распределения сенсорных впечатлений (Иган, 1983). Если же уверенность C нормировать по ее среднему квадратическому отклонению d’, то условные законы распределений g(u|sn) и g(u|n) для решений P(sn,Y|C), P(n,N|C) и вероятностей ошибочности решений P(n,Y|C), P(sn,N|C) от суммы свидетельств нормированной переменной u.

Решающее правило эвристической модели: при C > 0 принимается решение Y, иначе принимается решение N. u = C/d’ = (x – d’/2) + L0 /d’ (18) g(C|sn) и g(C|n) – нормальные законы распределения случайной величины C при событиях sn и n пределениями f(x|sn) и f(x|n) для x. При равновероятных событиях sn и n распределения g(u|sn) и g(u|n) расположены симметричным образом относительно оси ординат u = 0 (рис. 4). Выделение блока принятия решения. В полученной эвристической модели случайная сумма свидетельств C и случайное сенсорное впечатление от стимула x связаны простой линейной зависимостью (17). При этом зависимость (17) можно рассматривать как формулу перехода от нескольких независимых переменных сенсорного блока (x, d’ и L0) к единой собственной переменной C блока принятия решения. Ценность переменной C состоит в том, что ее одной оказалось вполне достаточно для описания всей работы блока принятия решения, который включает в себя решающее правило и формулу 0,5 +0,5 th[(|C|)/2] для оценки вероятности правильности принятого решения. Полученное ранее решающее правило для идеального наблюдателя просто прогнозирует наиболее вероятное из двух возможных событий sn и n, так, при любом C > 0 принимается решение Y, а при любом C < 0 принимается решение N. Однако в реальной жизни встречаются ситуации, требующие учета дополнительных условий при выборе решения. Блок принятия решения осторожного наблюдателя. В нашей работе проверяется гипотеза об уверенности как факторе, напрямую влияющем на правильность принимаемых решений. Если в какой-то пробе уверенность C оказалась слишком близкой к нулю, то вероятность правильности решения, вынесенного в этой пробе, лишь немного превышает вероятность его ошибочности. В этой ситуации рациональный наблюдатель, стремящийся снизить риск ошибочного решения и для этого контролирующий уровень своей уверенности, должен отказываться от принятия решения. Решающее правило осторожного наблюдателя, выносящего свои решения с учетом уверенности в их правильности, выглядит следующим образом: если C > CY > 0, то принимается решение Y; если C < CN < 0, то принимается решение N; если же CN < C < CY, то ни одно из решений Y или N не может быть принятым, так как вероятности их правильности слишком низки. Константа CY задает минимально допустимый уровень уверенности наблюдателя и, соответственно, минимально допустимый уровень вероятности правильности для принятого им решения Y, а CN задает минимальный уровень уверенности и вероятности правильности для решения N.

Анализ решающего правила осторожного наблюдателя. Безусловная вероятность правильности решения, принятого на основе такого правила, P(Conf) (confidence – уверенность) равна:
P(Conf) = P(sn,Y) + P(n,Y) + P(sn,N) + P(n,N). (19)

Интервал (CN, CY) задает зону сомнений на оси C. При попадании случайного значения C внутрь этой зоны решение в данной пробе не принимается. Отказ от принятия решения обозначим событием D (doubt – сомнение). Безусловная вероятность такого события P(D) равна: P(D) = 1 – P(Conf) = 1 – P(sn,Y) – P(n,Y) – P(sn,N) – P(n,N). (20)

Безусловная вероятность вынесения правильных решений P(Cor) вычисляется по формуле (10). При этом доля правильных решений среди уверенных равна P(Cor)/P(Conf).

Интервалу (CN, CY) по оси значений уверенности C однозначно соответствует интервал (uN, uY) по оси нормированных значений уверенности u. Если в соответствии с формулой (18) от сенсорного впечатления x, его распределений f(x|sn), f(x|n) и подмножеств XY, XN, X0, задающих области существования решений, перейти к нормированной уверенности u, ее распределениям g(u|sn), g(u|n) и соответствующим множествам UY = (uY, ∞), UN = (–∞, uzN), UD = (uN, uY), задающим на оси u соответствующие области реализации событий Y, N, D, то по аналогии с (10) можно получить P(Cor), выраженное через переменную u:
P(Cor) = P(sn,Y) + P(n,N) = ∫P(sn|u) g(u)du + ∫P(n|u) g(u)du = UY UN = P(sn) ∫g(u|sn)du + P(n) ∫g(u|n)du. (21)

При выводе формулы (21) использовались равенства, описывающие вероятность совпадения двух событий, аналогичные равенству (2):
P(sn|u) g(u)du = P(sn) g(u|sn)du и
P(n|u) g(u)du = P(n) g(u|n)du.
Аналогичным образом, переходя к оси u, можно конкретизировать выражение (19) для P(Conf):
P(Conf) = P(sn,Y) + P(n,Y) + P(sn,N) + P(n,N) =
= P(sn) ∫g(u|sn)du + P(n) ∫g(u|n)du + P(sn) ∫g(u|sn)du + P(n) ∫g(u|n)du. (22)

Интегралы от нормальных плотностей условных распределений g(u|sn) и g(u|n), входящие в (21) и (22), легко вычисляются через табличную функцию Лапласа.

Для проверки гипотезы о том, что человек с помощью повышения минимального уровня своей уверенности может повышать правильность своих решений, была получена теоретическая зависимость доли правильных решений среди всего массива уверенных решений P(Cor)/P(Conf) от ширины зоны сомнений Δu = uY – uN на нормированной оси принятия решения u. Полученные для равновероятных событий sn, n и заданного значения их различимости d’ = 1,4 зависимости P(Cor), P(Conf) и P(Cor)/P(Conf) от ширины зоны сомнений Δu приведены на рис. 5.

Итак, исходя из проведенного теоретического анализа эвристической модели принятия решения с оценкой уверенности, мы можем сделать следующий общий вывод: чем шире зона сомнений испытуемого на оси принятия решения (при неизменном числе проб), тем меньше среди ответов испытуемого остается уверенных ответов, однако, среди них чаще встречаются верные. Иначе говоря, позволяя наблюдателю отказываться от принятия уверенного решения в тех случаях, когда он чувствует неуверенность, можно существенно повысить правильность его уверенных решений.

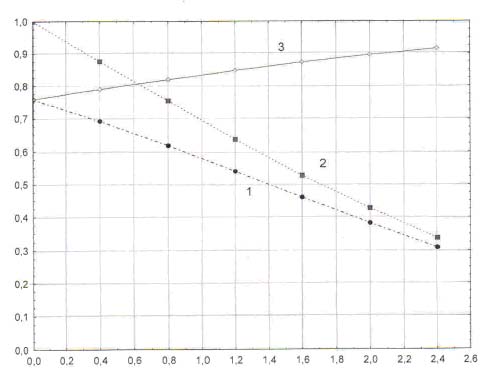
Рис. 5. Графики зависимостей вероятностей ответов от ширины зоны сомнений. Графики зависимостей вероятностей от ширины зоны сомнений Δu = u – u , отложенной по горизонтальной оси: 1 – вероятность вынесения правильного уверенного ответа P(Cor, Conf)); 2 – вероятность вынесения уверенного ответа P(Conf); 3 – доля правильных уверенных ответов среди всех уверенных ответов P(Cor, Conf),/P(Conf). Различимость событий sn, n, выбранная для проведения расчетов,равна d’ = 1,4
Полученные графики позволяют нетолько дать качественное описание этой закономерности, но и количественно оценить полезный эффект сомнений. Конечно, величина зоны сомнений экспериментатору да и самому наблюдателю неизвестна, поэтому заранее величину прибавки частоты правильных ответов предсказать невозможно. Однако теоретическая модель однозначно прогнозирует, что среди уверенных ответов наблюдателя частота правильных ответов будет всегда выше, чем в общем массиве ответов, где присутствуют как уверенные, так и неуверенные ответы.

Постановка задачи для экспериментальных исследований

Для верификации эвристической модели была проведена экспериментальная проверка полученной прогностической модели на материале решения наблюдателями задач порогового различения сенсорных признаков объектов.

Различение близких по величине признаков объектов представляет собой один из основных видов сенсорных задач, имеющий наиболее общий характер, тогда как две другие задачи – обнаружение и опознание по психологическому содержанию – представляют собой частные случаи различения (Забродин и др., 1981). Все перечисленные ситуации являются предметом изучения в психофизике, а в повседневной жизни типичны для деятельности операторов информационных панелей, разработчиков видео- и аудиотехники, врачей, занимающихся диагностикой и коррекцией зрения и слуха, рентгенологией, дегустаторов и т.п.

Собственно различение бывает двух типов: с ответами «больше–меньше» и с ответами «одинаковые–разные». Причем различение по типу «одинаковые–разные» в психофизике изучено гораздо меньше, чем «больше–меньше». Задачи порогового типа представляют собой предельную для человека ситуацию: когда сравниваемые признаки едва различимы, весьма острым является дефицит входной сенсорной информации, и потому высока субъективная неопределенность, что вызывает у человека неуверенность, сомнения в ходе решения задачи.

Для выяснения того, как влияют сомнения на вероятность правильности принимаемого решения, наши испытуемые выполняли две основные типовые задачи по различению (при сравнении) зрительных стимулов: «больше–меньше» для пространственных признаков при одновременном предъявлении стимулов и «одинаковые–разные» для временных признаков при последовательном предъявлении стимулов.

В рамках первой задачи были организованы две экспериментальные ситуации. В первой ситуации испытуемые, несмотря на свои сомнения в правильности принимаемого решения, должны были выбрать определенный ответ из двух взаимоисключающих альтернатив – «больше» или «меньше» (двухкатегорийный метод констант). Во второй ситуации испытуемые в случае сомнения в правильности принимаемого решения могли проявить осторожность и отказаться от принятия определенного решения путем вынесения ответа «сомневаюсь» (трехкатегорийный метод констант). Так как в случае этого ответа экспериментатор не имел возможности оценить правильность решения, то он просто регистрировал отказ от решения «больше» или «меньше».

Экспериментальное исследование уверенности и сомнений в задачах порогового различения

1. Задача «больше–меньше» Методика
Цель экспериментов (проведенных В.М. Шендяпиным) состояла в исследовании способности наблюдателя управлять правильностью решения сенсорной задачи с помощью уверенности в принятом решении. В психофизических экспериментах, состоящих из двух серий проб каждый с использованием двух- и трехкатегорийного вариантов метода констант (Бардин, 1976), соответственно, изучалось зрительное пороговое различение размеров окружностей, одновременно предъявлявшихся парами на экране монитора (методика В.А. Садова и В.М. Шендяпина, компьютерная программа В.А. Садова).

Характеристики стимуляции: величина эталонной окружности, предъявлявшейся всегда слева от переменной, составляла 275 или 375 пикселей (в зависимости от размера дисплея используемого компьютера). Два значения размера окружности переменного диаметра – большее и меньшее, чем размеры эталонной (т.е. две константы), – индивидуально подбирались околопороговыми для каждого наблюдателя; в результате при предъявлении и той, и другой (в парах с эталоном) было суммарно получено 54–80% правильных ответов. Диапазон размеров окружности переменного диаметра составлял от 268 до 279 пикселей. Предъявления обеих пар стимулов (с той и другой константой) были равновероятными (Р= Р = 0,5) и происходили в случайном порядке. Длительность предъявления пары стимулов составляла 600 мс, а временной интервал между пробами – 1000 мс.

Процедура, испытуемые. В исследовании участвовали 47 испытуемых, с каждым из которых было проведено от 1 до 7 экспериментов, включавших по 2 серии проб. 36 экспериментов включали серии по 400 проб каждый, 11 – по 300, 1 –299, 6 –по 200 и 37 – по 100 проб. При этом вторая серия содержала не меньше, а обычно больше проб, чем первая, так, чтобы число уверенных ответов во второй серии было соизмеримо с числом всех ответов в первой серии. Варьирование количества было вызвано, с одной стороны, стремлением получить максимально возможную статистику измерений, а с другой – ориентацией на степень зрительной утомляемости испытуемых. Тем, кто испытывал сильное утомление при предъявлении последовательности из 400 проб, количество проб снижалось до 300, 200 или 100, в зависимости от функционального состояния в ходе опытов. Таким образом, в целом был проведен 91 эксперимент, что составило 22799 психофизических измерений по двухкатегорийному варианту метода констант и 23814 психофизических измерений по трехкатегорийному варианту, т.е. в общей сложности 46613 измерений.

В первой серии наблюдатели при предъявлении каждой пары стимулов выносили ответ, используя одну из двух категорий: «больше» или «меньше» окружность переменного диаметра по сравнению с эталонной. Во второй серии испытуемые для каждой пары стимулов давали ответ в этих двух категориях только в тех случаях, когда были в нем уверены. В случаях неуверенности они давали ответ «сомневаюсь».

Инструкция для первой серии, соответствующей первой экспериментальной ситуации. «В эксперименте изучается ваша индивидуальная способность управлять процессом принятия своих сенсорных решений для обеспечения успешности деятельности, в которую вы в данный момент включены. Предполагается, что успешность вашей деятельности зависит только от того, насколько точно вы различаете предъявляемые на правой половине экрана компьютера два круга, радиусы которых слегка различаются. Чем больше правильных и чем меньше ошибочных ответов вы дадите, тем выше будет оценка результатов вашей деятельности.

Эксперимент состоит из последовательности проб. В каждой пробе в левой и правой половинах экрана монитора одновременно предъявляются две окружности. Слева всегда появляется одна и та же окружность эталонного размера. Справа появляется окружность переменного размера, большего или меньшего, чем эталон. Большие и меньшие окружности предъявляются в случайном порядке с одинаковой вероятностью, равной 0,5. Размеры переменных окружностей подбираются индивидуально, так, чтобы в серии из 100 проб суммарно получалось 70–80% правильных ответов.
Ваша цель: максимально точно рассортировать окружности переменного размера на две категории – «большие» и «меньшие», чем эталон. В каждой пробе ваша задача – дать ответ: окружность переменного размера (правый круг) вы относите к «большим» (нажимаете клавишу →) либо к «меньшим» (нажимаете клавишу ←). Программа устроена так, что ваш ответ засчитывается только после того, как предъявленная в пробе пара кругов исчезла с экрана. Время для вашего ответа не ограничивается. Важно, чтобы вы давали наиболее точный ответ (а не наиболее быстрый). Следующая пара стимулов будет появляться после вашего ответа на предъявление предыдущей пары окружностей. Пожалуйста, внимательно наблюдайте за предъявляемыми сигналами и старайтесь отвечать как можно точнее.»

Инструкция для второй серии, соответствующей второй экспериментальной ситуации, повторяла инструкцию для первой с одним отличием: для каждой пары стимулов выносились те же два ответа «больше» либо «меньше», но только при условии уверенности испытуемого в их правильности. При этом испытуемым предлагалось добиваться максимально высокого уровня правильности решения. Например, женщинам предлагалась ролевая игра врача, ставящего на основании сравнения предъявленных окружностей диагноз серьезно больному человеку. А мужчинам предлагалось играть роль охотника, который в случае промаха безвозвратно теряет дичь, в которую он целится через оптический прицел с двумя окружностями. В случаях же неуверенности в решении испытуемым разрешалось выносить ответ «сомневаюсь» путем нажатия на клавишу ↑. Так как определенное решение в данной пробе отсутствует, то считалось, что никаких событий в реальном мире при этом не происходит. Тем самым испытуемый избегал риска принятия ошибочного решения в данной пробе, но при этом сокращал общее число принятых в данной серии решений. Статистические процедуры обработки и анализа полученных данных состояли в следующем:
1. Для каждого отдельного эксперимента: а) подсчитывалось общее число полученных ответов n1 и число правильных ответов m1 среди них в первой серии, число уверенных ответов n2 и число правильных ответов m2 среди них во второй серии; б) в качестве оценки вероятности правильности ответа в первой серии вычислялась частота w = m/ n, в качестве оценки вероятности правильности ответа во второй серии p2 вычислялась частота правильных среди уверенных ответов w = m/ n, в качестве оценки Δp = p – p – величины прибавки вероятности p2 относительно p1 – вычислялась величина сдвига второй частоты относительно первой Δw = w2 – w1; в) для контроля ошибок, возникающих при замене вероятностей p1, p2 на частоты w1, w2 , вычислялись оценки соответствующих средних ]}1/2 и σ квадратических отклонений σ = {[w (1 – w)/n = {[w (1 – w)/n]}1/2, для контроля ошибки, возникающей при замене Δp на Δw, вычислялась оценка среднего квадратического отклонения σΔ = (σ12 + σ22)1/2 (Гмурман, 1999).

2. По результатам всех экспериментов выделены максимальные и минимальные значения w1, w2 и Δw, определяющие размах вариации этих показателей по всей выборке полученных результатов.

Для проверки, в какую сторону в целом по всей полученной в результате экспериментов выборке Δw сдвигаются оценки w2 вероятности p2 относительно оценки w1 вероятности p1, использовался непараметрический критерий знаков (Сидоренко, 1996). Метод непараметрической статистики использован потому, что он не чувствителен к виду распределения эмпирических данных и оттого более универсален, чем параметрические методы, адекватные лишь для нормальных распределений.

Результаты и их обсуждение

Упорядоченные по возрастанию прибавки Δw, полученные в 91 эксперименте, представлены на рис. 6 средней, монотонно растущей последовательностью экспериментальных точек. Верхние и нижние немонотонно разбросанные точки оценивают диапазон вариативности полученных значений: Δw ± σΔ. Видно, что практически все полученные значения Δw расположены в области положительных значений.

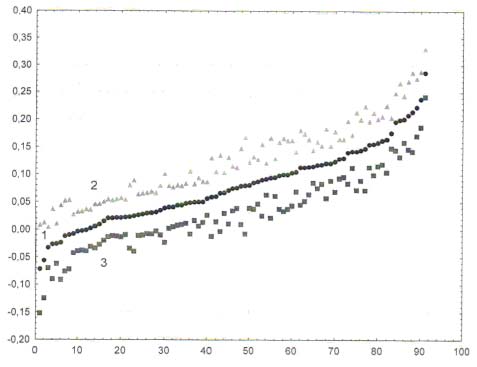
Рис. 6. Результаты 91 эксперимента в задаче «больше–меньше»: 1 – упорядоченная по возрастанию последовательность прибавок Δw индивидуальных значений частот w2 правильных ответов, полученных при выборе из 3-х категорий: «больше– меньше–сомневаюсь», относительно частот w1 правильных ответов, полученных при выборе из 2-х категорий: «больше–меньше». Последовательности точек 2, 3 показывают диапазон вариативности полученных значений прибавок Δw ± σΔ

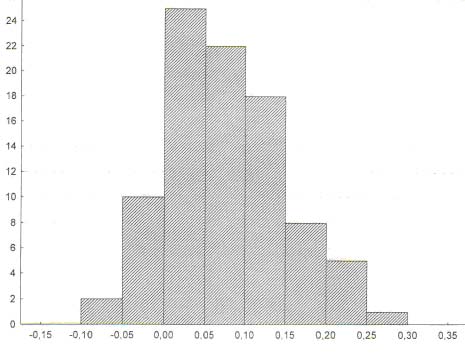
Рис. 7. Гистограмма распределения прибавок Δw индивидуальных значений частот w2 правильных ответов, полученных при выборе из 3-х категорий: «больше–меньше–сомневаюсь», относительно частот w1 правильных ответов, полученных при вы- боре из 2-х категорий: «больше–меньше»

На рис. 7 представлена частотная гистограмма распределения индивидуальных величин Δw, соответствующих средней, монотонно растущей последовательности точек, представленной на рис. 6.

Как видно из рис. 7, в подавляющем большинстве экспериментов (в 79 из 91, или в 87% случаев) обнаружено превышение частоты правильных ответов w2 над частотой правильных ответов w1.

Показатели, оцененные по всему массиву полученных значений частот, приведены в табл. 1. Среднее по всему массиву экспериментов значение частоты правильных среди уверенных ответов: w2ср = 0,762 превышает среднее значение частоты всех правильных ответов: w1ср = 0,683 на величину Δwср = 0,078, т.е. почти на 8%. Размах разброса величин Δw по всему массиву экспериментов составил от -0,072 до 0,287, т.е. от -7,2 до 28,7%.

Таблица 1. Задача «больше–меньше». Оцененные по всему массиву из 91 эксперимента показатели частот w1 правильных ответов, полученных в первом эксперименте, частот w2 правильных уверенных ответов, полученных во втором эксперименте, и прибавок Δw = w2 – w1

Для проверки гипотезы о том, что преимущественно положительные знаки сдвига частот правильных среди уверенных ответов w2 относительно частот всех правильных ответов w1 могли быть получены случайно, использовался непараметрический G-критерий знаков. Согласно методу критерия знаков подсчитывается число «нетипичных» отрицательных знаков сдвига G , которое затем сравнивается с критическим значением G , зависящим от общего числа полученных сдвигов и заданного уровня значимости α при проверке гипотезы. Если G < G, то гипотеза о случайном характере положительных сдвигов должна быть отвергнута (Сидоренко, 1996).

Для наших данных (общее число полученных сдвигов равно 91) и уровня значимости α = 0,01 табличное значение G = 33. Так как значение G, найденное в эксперименте, оказалось равным 12, то преимущественно положительные знаки сдвига частот правильных ответов получены не случайно, а благодаря предоставленной испытуемым возможности отказываться от принятия решений в тех ситуациях, когда они не уверены в их правильности. Таким образом, сравнение результатов, полученных в первой и второй сериях, свидетельствует о том, что испытуемые способны управлять правильностью решения сенсорной задачи с помощью уверенности в принятом решении.

2. Задача «одинаковые–разные» Методика
В.М. Шендяпиным проанализированы данные исследований И.Г. Скотниковой (2002, 2005, 2008) и Е.В. Головиной (2006, 2009), полученные для различения по типу «одинаковые–разные» (метод «same–different»).

Характеристики стимуляции. В психофизическом эксперименте изучается зрительное пороговое различение временных интервалов, задаваемых парами последовательных световых вспышек голубого люминесцентного индикатора прямоугольной формы яркостью около 20 нит и угловым размером 11,5°. В случайном порядке предъявлялись пары равных либо едва различающихся по длительности стимулов (методика И.Г. Скотниковой, В.А. Чурсинова, А.Н. Костина, В.А. Садова, – см.: Скотникова, 2005). Стимулы предъявлялись на экранах мониторов, работающих в монохромном режиме с разрешением 800×600 пикселей. Эксперимент проводился в автоматическом режиме. Использовалась экспериментальная парадигма «да–нет» с процедурой различения «одинаковые–разные» (same–different) и техникой лестниц для определения разностного порога. Длительность одного сигнала всегда составляла 600 мс («нейтральный интервал», наиболее адекватно воспринимаемый человеком) (Фресс, 1978), длительность другого (600 мс–Δt) подбиралась индивидуально для каждого испытуемого в предварительных сериях как соответствующая традиционному разностному порогу Δt для 70–80%-ного правильного различения (величины порогов индивидуально варьировали в диапазоне 55–250 мс). Погрешность формирования длительностей стимулов не превышала 0,008 с, т.е. 1–2% от их значений. Пары одинаковых (по 600 мс каждый) и разных стимулов (600 мс и 600 мс–Δt), а также место более длительного стимула в парах разных стимулов были равновероятны и чередовались в случайном порядке. Интервал между вспышками в паре составлял 1 с, время на ответ (интервал между парами) не ограничивалось (очередная пара стимулов предъявлялась после ответа испытуемого на предыдущую пару).

Процедура. Каждому испытуемому после тренировки в предварительной серии предъявлялись 7 величин Δt в диапазоне 100–300 мс шагами по 25 мс в блоках, состоящих из 10–30 проб каждый (всего не менее 70 проб в серии). После определения индивидуального порога испытуемого и тренировочных опытов с использованием выбранной индивидуальной величины Δt проводился основной опыт из 100 проб.

В каждой пробе испытуемые, согласно инструкции, давали два ответа: 1) оценивали длительности в каждой паре как «одинаковые» или «разные» и 2) оценивали, уверены или сомневаются они в правильности первого ответа, т.е. в правильности различения. Инструкция ориентировала испытуемых давать возможно более точные ответы. Фиксировался характер каждого моторного ответа.

Испытуемые, статистика измерений. По материалам исследований И. Г. Скотниковой проанализированы данные 55 экспериментов 2000–2001 годов (5500 измерений), по материалам исследований Е.В. Головиной – данные 43 экспериментов 1999–2003 годов (4300 измерений). В них участвовали соответственно 39 и 32 испытуемых с нормальным или скорректированным зрением, мужчины и женщины в возрасте 19–28 лет, студенты и сотрудники немецких (университетов Геттингена и Мюнхена, ФРГ) и российского (ГУГН) вузов. Общее число экспериментов составило 98, измерений – 9825 (один эксперимент включал не 100 проб, как все остальные, а 125), испытуемых – 71 человек.

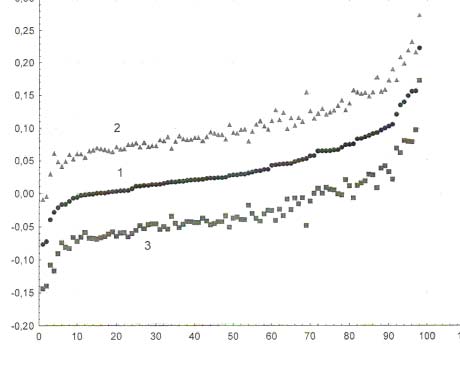
Рис. 8. Результаты 98 экспериментов в задаче «одинаковые–разные»: 1 – упорядоченная по возрастанию последовательность прибавок Δw индивидуальных значений частот w2 правильных уверен-ных ответов относительно частот w1 всех (уверенных и неуверенных) правильных ответов. Последователь- ности точек 2, 3 показывают диапазон вариативности полученных значений прибавок Δw ± σΔ

Приведем ниже статистические процедуры обработки и анализа полученных данных.

По индивидуальным данным каждого испытуемого, а также по всему массиву данных (9825 измерений): а) подсчитывалось общее число полученных ответов n1 и число правильных m1 среди всех ответов, число уверенных ответов n2 и число правильных m2 среди уверенных ответов; б) вычислялись: частота всех правильных ответов w1 = m1 /n1, частота правильных среди уверенных ответов w = m/n и их разность Δw = w – w; выделены максимальные и минимальные значения w1, w2 и Δ, определяющие размах вариации этих показателей; в) вычислялись оценки соответствующих средних квадратических отклонений σ1, σ2 и σΔ для значений w1, w2 и Δw тем же способом, что и для данных, полученных в задаче «больше– меньше» (Гмурман, 1999). Статистическая значимость неслучайности различий между частотами правильных ответов (w1) и правильных среди уверенных ответов (w2) оценивалась с помощью непараметрического критерия знаков (Сидоренко, 1996). Поскольку общей целью исследования, представленного в настоящей статье, было сопоставление частот правильных ответов w1 среди всех ответов и частот правильных ответов w2 среди уверенных ответов, то включение в анализ только данных, попавших в диапазон величин w1, равный 70–80% правильных ответов, было не обязательным. Поэтому в статистический анализ данных всех 98 экспериментов, как и в задаче «больше–меньше (сомневаюсь)», вошли данные экспериментов, где обнаружены не только пороговые, но и околопороговые величины w1. Они распределились в диапазоне 61–87%.

Результаты и их обсуждение

Упорядоченные по возрастанию значения прибавки Δw, полученные в каждом из 98 экспериментов, представлены на рис. 8 средней, монотонно растущей последовательностью экспериментальных точек. Верхние и нижние немонотонно разбросанные точки задают диапазон вариативности полученных значений: Δw ± σΔ. Вновь очевидно, что практически весь диапазон значений Δw расположен в области положительных значений.

Однако в целом эти значения несколько меньше (они расположены в области более низких величин Δw), а их разброс, т.е. среднее квадратическое отклонение σΔ, больше по сравнению с результатами, полученными в задаче «больше–меньше (сомневаюсь)» (рис. 6). Большие значения Δw в задаче «больше– меньше (сомневаюсь)» объясняются тем, что в этой задаче испытуемые более осознанно управляли своей уверенностью (см. раздел «Влияние инструкции на прибавку частоты правильных ответов»). Больший разброс величин Δw в задаче «одинаковые–разные» – следствие меньшего объема измерений, проведенных с каждым испытуемым, по сравнению с задачей «больше–меньше (сомневаюсь)».

На рис. 9 представлена частотная гистограмма распределения индивидуальных значений Δw, соответствующих средней кривой на рис. 8.

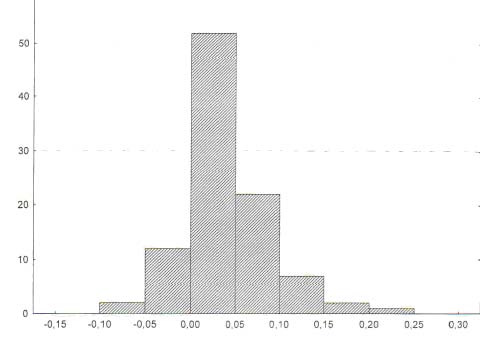
Рис. 9. Гистограмма распределения 98 индивидуальных прибавок Δw значений частот w2 правильных уверенных ответов относительно частот w1 всех (уверенных и неуверенных) правильных ответов

Как видно из рис. 9, вновь в подавляющем большинстве экспериментов (в 84 из 98, т.е. в 85% случаев) частота правильных ответов среди уверенных оказалась выше, чем общая по всем ответам частота правильных ответов. Показатели, найденные по всему массиву полученных значений частот, представлены в табл. 2. Среднее по всем экспериментам значение частоты правильных ответов среди уверенных w2ср = 0,773 превышает среднее значение частоты правильных среди всех ответов w = 0, 734 на величину Δw = 0,039, т. е.почти на 4%. Размах разброса величин Δw, полученный по всем экспериментам, составил от -0,0764 до 0,224, т. е. от -7,6% до 22%.

Таблица 2. Задача «одинаковые–разные». Оцененные по всему массиву из 98 экспериментов показатели частот w1 всех (уверенных и неуверенных) правильных ответов, частот w2 правильных уверенных ответов и прибавок Δw = w2 – w1

Гипотеза о неслучайности полученного в экспериментах большого числа положительных сдвигов Δw частот w2 правильных уверенных ответов относительно частот w1 всех (уверенных и неуверенных) правильных ответов, проверенная по критерию знаков, значимо подтвердилась. Число «нетипичных» отрицательных сдвигов (Gэмп = 14) оказалось намного меньше критического значения (Gкр = 37), соответствующего нашему массиву данных (общее число сдвигов равно 98) и уровню значимости α = 0,01.

Влияние инструкции на прибавку частоты правильных ответов

Эффективность осознанного управления правильностью решения сенсорной задачи с помощью уверенности была обнаружена при сравнении сдвигов, полученных в двух рассмотренных задачах. Использование инструкции, которая прямо стимулирует испытуемых стремиться к максимальной правильности уверенного решения (в задаче «больше–меньше» с разрешением ответов «сомневаюсь» по методике Шендяпина), позволило получить усредненный по всем экспериментам сдвиг частоты правильных ответов (среди уверенных) относительно общей частоты правильных ответов (Δwср = 0,078), вдвое больший аналогичного усредненного по всем экспериментам сдвига в случае инструкции, в которой уверенность нейтральна по отношению к повышению правильности (в задаче «одинаковые–разные» по методике Скотниковой: Δwср = 0,039). Так как сам по себе этот факт еще не обеспечивает достоверности вывода о больших прибавках в подзадаче «больше–меньше–сомневаюсь», то для проверки гипотезы о том, что величина сдвига частот Δw в целом по всем экспериментам подзадачи «больше—меньше–сомневаюсь» значимо превышает величину сдвига частот Δw по всем экспериментам задачи «одинаковые–разные», был использован непараметрический U-критерий Манна-Уитни.

Сравнение сдвигов частот Δw по 91 эксперименту подзадачи «больше–меньше– сомневаюсь» со сдвигами частот Δw по 98 экспериментам задачи «одинаковые–разные», выполненное с помощью U-критерия, выявило, что сдвиги, полученные в задаче «одинаковые– разные», статистически достоверно (p <0,00003) ниже сдвигов, полученных в подзадаче «больше–меньше–сомневаюсь».

Важно отметить, что превышение правильности уверенных ответов над правильностью всех ответов обнаружено в обоих основных видах задач зрительного различения: по шкале «больше–меньше» (включая также ответы «сомневаюсь») и по шкале «одинаковые– разные», причем как для пространственных признаков зрительных объектов, предъявлявшихся одновременно, так и для временных признаков, предъявлявшихся последовательно. Таким образом, установленный факт имеет достаточно общее значение.

Пилотажное исследование взаимосвязи между способностью испытуемых повышать правильность ответов с помощью уверенности и свойствами их индивидуальности

Цель исследования. Способность повышать частоту правильных ответов с помощью рефлективных переживаний уверенности–сомнений сильно варьирует даже среди испытуемых, которых специально инструктировали на высокую прибавку правильности (в экспериментах по зрительному различению размеров окружностей в задаче «больше– меньше» с разрешением ответов «сомневаюсь». Некоторые испытуемые совсем не могли справиться с поставленной задачей (пропорция правильных ответов у них не менялась, либо даже уменьшалась), в то время как другие значительно увеличивали частоту правильных ответов (например, с 0,72 до 0,96), т.е. почти до максимума. Для выяснения, существуют ли взаимосвязи между способностью испытуемых увеличивать точность решения сенсорной задачи при использовании только уверенных ответов, с одной стороны, и свойствами их индивидуальности – с другой, В. М. Шендяпиным была проведена пилотажная диагностическая серия экспериментов по оценке характеристик когнитивных стилей испытуемых.

Методики диагностической серии экспериментов

В диагностической серии экспериментов для 11 испытуемых из тех, которые участвовали в психофизических экспериментах В.М. Шендяпина по зрительному различению размеров окружностей в задаче «больше–меньше», определялись индивидуальные характеристики двух когнитивных стилей: «рефлективность–импульсивность» по тесту подбора сходных фигур Кагана (Kagan, 1966) и опроснику В.Н. Азарова (1983), а также «ригидность–гибкость» познавательного контроля по тесту вербально-цветовой интерференции Струпа (Stroop, 1935) и опросникам Айзенка-Белоуса и Бренгельмана (Залевский, 1976, 2007). Вычислялись стандартные показатели когнитивных стилей, принятые при использовании перечисленных методик. Дополнительно к стилевым характеристикам определялась индивидуальная склонность к риску по опроснику Когана-Валлаха.

Стиль «рефлективность–импульсивность». По данным теста Кагана определялось среднее по первым шести картам время первого ответа T1 и суммарное по этим картам число ошибок nош. По данным опросника Азарова оценивался индекс импульсивности Иимп.

Чем больше время первого ответа и меньше число ошибок в тесте Кагана и чем выше индекс Азарова, тем выше рефлективность и ниже импульсивность.

Стиль «ригидность–флексибильность». По данным теста Струпа определялась разность (T3 – T2) – величина прироста времени выполнения третьей (конфликтной) пробы по сравнению со временем выполнения второй (фоновой) пробы и (T3 – T2)/T2 – величина прироста времени выполнения третьей пробы по отношению ко времени выполнения второй пробы. По данным опросников Бренгельмана и Айзенка-Белоуса оценивался суммарный по обеим методикам показатель ригидности Приг.

По опроснику Когана-Валлаха определялся индивидуальный показатель склонности к риску Ириск.

Проводился ранговый корреляционный анализ с целью выяснения, существуют ли значимые взаимосвязи между индивидуальными показателями: изменения успешности решения сенсорной задачи при использовании уверенных ответов (Δw – разностью между частотой правильных ответов среди уверенных w2 и частотой всех правильных ответов w1), с одной стороны, и показателями свойств индивидуальности испытуемых – с другой. Корреляция оценивалась тремя способами: по коэффициенту корреляции Спирмена и по статистикам Гамма и тау Кендалла. Кроме того, для выявления более сложных взаимосвязей между способностью испытуемых увеличивать точность решения сенсорной задачи и свойствами их индивидуальности проводился пилотажный факторный анализ.

Отметим, что специфика психофизических исследований такова, что требуется большая статистика измерений для каждого наблюдателя в целях получения достоверных показателей сенсорного исполнения. Поэтому подобные эксперименты проводятся, как правило, с участием хоть и небольшого количества испытуемых, но хорошо тренированных.

Соответственно, дифференциально-психофизические исследования выполняются обычно с участием не сотен испытуемых, как принято в дифференциально-психологических работах (когда с каждым проводится 1–2 измерения по конкретной методике), а лишь десятков и даже менее десяти, что достаточно для получения значимых результатов в силу большого объема сенсорных измерений. Например, в исследованиях Т.П. Войтенко (1991) с участием 14 испытуемых и И. Г. Скотниковой (Кочетков, Скотникова, 1993) с участием 13 и 7 испытуемых были установлены значимые корреляционные взаимосвязи между показателями обнаружения звукового сигнала на фоне шума и поле(не)зависимого, а также ригидного–гибкого когнитивных стилей в первом случае и между показателями различения зрительных стимулов и поле(не)зависимого, а также рефлективного–импульсивного стилей во втором случае.

Результаты и их обсуждение

В результате рангового корреляционного анализа данных психофизических и диагностических экспериментов выяснилось, что значимо коррелирует с величиной Δw только показатель nош в тесте Кагана на оценку импульсивности.

При вычислении корреляции по Спирмену коэффициент корреляции между ними оказался равным r = -0,60054 при p = 0,05074. Показатель ригидности по тесту Струпа (T3 – T2)/T2) коррелирует с Δw незначимо: r = -0,5 при p = 0,117307. Для остальных показателей корреляция с Δw не является статистически значимой.

При вычислении корреляции с помощью статистики Гамма связь между Δw и nош теста Кагана оценивается величиной r = -0,510204 при p = 0,039211. Показатель склонности к риску Ириск по опроснику Когана-Валлаха коррелирует с Δw слабее: r = 0,444444 и менее значимо: p = = 0,059346. Для остальных показателей корреляция с Δw не является статистически значимой.

При вычислении корреляции с помощью статистики тау Кендалла связь между Δw и nош в тесте Кагана оценивается величиной r = -0,481571 при p = 0,039211. Показатель склонности к риску Ириск по опроснику Когана-Валлаха вновь коррелирует с Δw слабее: r = 0,440386 и менее значимо: p = 0,059346. Для остальных показателей корреляция с ΔP не является статистически значимой.

При проведении факторного анализа число учитываемых факторов варьировалось от 1 до 3. Выделенные в результате анализа факторы и их нагрузки на переменные приведены в табл. 3–5. Жирным шрифтом выделены нагрузки, превышающие значимый уровень 0,7.

Таблица 3. Результаты факторного анализа для одного учитываемого фактора

Таблица 4. Результаты факторного анализа для двух учитываемых факторов

Таблица 5. Результаты факторного анализа для трех учитываемых факторов

Во всех трех случаях увеличение точности решения сенсорной задачи, описываемое переменной Δw, входит только в первый наиболее значимый фактор. Кроме переменной Δw в этот фактор всегда значимо входят показатели теста Кагана и индекс импульсивности Азарова. Таким образом, первый фактор можно условно назвать «импульсивностью– рефлективностью» испытуемых. Остальные два фактора связаны с переменной Δw очень слабо. Один из них отражает стиль «ригидность–флексибильность» по тесту Струпа, а второй – склонность к риску по опроснику Когана-Валлаха. Суммарный же по опросникам Айзенка-Белоуса и Бренгельмана показатель ригидности имеет довольно сильную тенденцию к включению в первый фактор и слабо коррелирует с остальными факторами. На эту тенденцию следует обратить внимание и проверить ее дополнительно.

Проведенный анализ позволяет сделать вывод о том, что индивидуальная способность наблюдателя осознанно управлять правильностью решения сенсорной задачи с помощью уверенности в принятом решении у рефлективных лиц выше, чем у импульсивных. Этот факт можно объяснить предположением, что у импульсивных лиц по сравнению с рефлективными более низкий (либеральный) критерий вынесения ответа об уверенности (более близкий к критерию вынесения основного ответа о сходстве или различии стимулов), которым они, по-видимому, не способны эффективно управлять в силу недостаточной сформированности механизмов наблюдения за своим поведением, его контроля и регуляции. Более развернутый анализ несформированности таких механизмов у импульсивных субъектов представлен М. А. Холодной (2004).
Предложенная интерпретация позволяет объяснить экспериментальные данные Скотниковой (2005, 2008) и Головиной (2006, 2009) о большей сверхуверенности импульсивных лиц в своих сенсорных суждениях по отношению к правильности этих суждений по сравнению с рефлективными, что может приводить первых к поверхностному анализу входной информации и потому сниженным показателям чувствительности (Скотникова, 1999). Действительно, их повышенная сверхуверенность может быть следствием более низких порогов принятия уверенных решений, чем у рефлективных субъектов.

Выводы

В разработанной для описания процесса выполнения сенсорных задач математической модели принятия решения с оценкой уверенности в его правильности теоретически обосновано, что величина уверенности в выбранной альтернативе решения может быть сведена к сумме эвристических свидетельств, накопленных в пользу этой альтернативы.

Предложенная модель прогнозирует, что вероятность правильности уверенных ответов превышает вероятность правильности всех (уверенных и неуверенных) ответов.

В экспериментальном исследовании выполнения обоих основных видов задач сенсорного различения: по шкале «больше–меньше» и по шкале «одинаковые–разные» как для пространственных, так и для временных признаков стимулов установлено, что среди уверенных ответов наблюдателей больше правильных, чем среди всех (уверенных и неуверенных) ответов, что подтверждает предсказание модели.

Использование инструкции, которая прямо стимулирует испытуемых стремиться к максимальной правильности уверенного решения, позволяет получить большее увеличение частоты правильных ответов, чем в случае инструкции, в которой уверенность нейтральна по отношению к повышению правильности. Это указывает на эффективность осознанного управления правильностью решения сенсорной задачи.

1. Азаров В.Н. Анкетная методика измерения импульсивности // Новые исследования в психологии. 1983. Вып. 29 (2). С. 15–19.
2. Барабанщиков В.А. Принцип системности в современной психологии: основания, проблемы, тенденции развития // Идея системности в психологии / Под ред. В.А. Барабанщикова. М.: Изд-во «Институт психологии РАН», 2005. С. 9–47.
3. Бардин К.В. Проблема порогов чувствительности и психофизические методы. М.: Наука, 1976.
4. Войтенко Т.П. Сенсорная тренировка как фактор развития чувствительности: Дисс. ... канд. психол. наук. М., 1989.
5. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа. 1999.
6. Головина Е.В. Структура уверенности и когнитивные стили: Дисс. ... канд. психол. наук. М., 2006.
7. Головина Е.В. Уверенность и адекватность ее оценки при решении сенсорной задачи: когнитивно-стилевой аспект // Современная психофизика / Под ред. В.А. Барабанщикова. М.: Изд-во ИП РАН, 2009. Гл. 22. С. 461–473.
8. Забродин Ю.М., Фришман Е.З., Шляхтин Г.С. Особенности решения сенсорных задач человеком. М.: Наука, 1981.
9. Залевский Г.В. Фиксированные формы поведения. Иркутск: Восточно-Сибирское книжное изд-во, 1976.
10. Залевский Г.В. Личность и фиксированные формы поведения. М.: Изд-во «Институт психологии РАН», 2007.
11. Иган Дж. Теория обнаружения сигналов и анализ рабочих характеристик. М.: Наука, 1983.
12. Карпов А.В. Психология принятия решения. Ярославль, 2003.
13. Козелецкий Ю. Психологическая теория решений. М.: Прогресс, 1979.
14. Кочетков В.В., Скотникова И.Г. Индивидуально-психологические проблемы принятия решения. М.: Наука, 1993.
15. Ломов Б.Ф. Математика и психология в изучении процессов принятия решений // Нормативные и дескриптивные модели принятия решения. М.: Наука, 1981.
16. Сидоренко Е.В. Методы математической обработки в психологии. СПб.: Социально-психологический центр, 1996.
17. Скотникова И.Г. Зрительное различение и импульсивность–рефлективность // Психологический журнал. 1999. Т. 20. № 4. С. 82–89.
18. Скотникова И.Г. Проблема уверенности – история и современное состояние // Психологический журнал. 2002. Т. 23. № 1. С. 52–60.
19. Скотникова И.Г. Экспериментальное исследование уверенности в решении сенсорных задач // Психологический журнал. 2005. Т. 26. № 3. С. 84–99.
20. Скотникова И.Г. Проблемы субъектной психофизики / Под ред. В.А. Барабанщикова. М.: Изд-во «Институт психологии РАН», 2008. Тверски А.,
21. Канеман Д. Принятия решений в условиях неопределенности: правила и предупреждения // Принятия решений в неопределенности / Под ред. Д. Канемана, П. Словика, А. Тверски. Харьков: Гуманитарный центр, 2005. C. 17–36.
22. Фресс П. Восприятие и оценка времени // Фресс П., Пиаже Ж. Экспериментальная психология. Вып. VI. Гл. XIX. М.: Прогресс, 1978. С. 88–135.
23. Холодная М.А. Когнитивные стили. О природе индивидуального ума. СПб.: Питер, 2004.
24. Шендяпин В.М. Сенсорное различение: математическое моделирование // Психофизика сегодня / Под ред. В.Н. Носуленко, И.Г. Скотниковой. М.: Изд-во «Институт психологии РАН», 2007. С. 123–135.
25. Шендяпин В.М. Использование теории обнаружения сигнала для разработки модели уверенности при решении сенсорных задач // Математическая психология: школа В.Ю. Крылова / Под ред. А.Л. Журавлева, Т.Н. Савченко, Г.М. Головиной. М.: Изд-во «Институт психологии РАН». 2010. С. 471–481.
26. Шендяпин В.М., Барабанщиков В.А. Использование теории обнаружения сигнала для разработки модели принятия решения человеком // Психология. Журнал Высшей школы экономики. 2008. Т. 5. № 3. С. 145–156.
27. Шендяпин В.М., Скотникова И.Г. Моделирование уверенности в процессе принятия решения // Интегрированные модели и мягкие вычисления в искусственном интеллекте. Сборник трудов Второго Международного научно-практического семинара. М.: Физматлит, 2003. C. 362–368.
28. Шендяпин В.М., Скотникова И.Г. Математическое моделирование принятия решения и уверенности при выполнении сенсорных задач // Новости искусственного интеллекта. 2006. № 2. С. 5–13.
29. Шендяпин В.М., Скотникова И.Г., Барабанщиков В.А., Тарасов В.Б. Математическое моделирование уверенности при принятии решения в сенсорных задачах // Психологический журнал. 2008. № 4. С. 84–97.
30. Adams J.K. A confidence scale defined in terms of expected percentages // American Journal of Psychology. 1957. V. 70. P. 432–436.
31. Balakrishnan J.D., Ratcliff R. Testing models of decision making using confidence ratings in classification // Journal of Experimental Psychology: Human Perception and Performance. 1996. V. 22. P. 615–633.
32. Bjorkman M., Juslin P., Winman A. Realism of confidence in sensory discrimination: The underconfidence phenomenon // Perception & Psychophysics. 1993. V. 54. P. 75–81.
33. Ferrel W.R. A model for realism of confidence judgments: implications of underconfidence in sensory discrimination // Perception & Psychophysics. 1995. V. 57. P. 246–254.
34. Ferrell W.R., McGoey P.J. A model of calibration for subjective probabilities // Organizational Behavior and Human Performance. 1980. V. 26. P. 32–53.
35. Green D.M., Swets J.A. Signal detection theory and psychophysics. N.Y.: Wiley, 1974.
36. Heath R.A. Random-walk and accumulator models of psychophysical discrimination: a critical evaluation // Perception. 1984. V. 13. P. 57–65.
37. Heath R.A., Fulham R. An adaptive filter model for recognition memory // British Journal of Mathematical and Statistical Psychology. 1988. V. 1. P. 119–144.
38. Kagan J. Reflection–impulsivity: the generality of dynamics of conceptual tempo // Journal of Abnormal Psychology. 1966. V. 71. P. 17–24.
39. Lacouture I., Marley A.A.J. Non-linear decision process in absolute identification // Fechner Day’2000: Proceedings of the 10th Annual Meeting of the International Society for Psychophysics. (ISP) / Ed. by C. Bonnet. Strasbourg: France, 2000. P. 91–96.
40. Link S. W. C. S. Pierce, confidence and random walk theory // Fechner Day’2003: Proceedings of the 13th Annual Meeting of the International Society for Psychophysics. (ISP) / Ed. by B. Berglund, E. Borg. Larnaka: Cyprus, 2003. P. 151–156.
41. Link S.W., Heath R.A. A sequential theory of psychological discrimination // Psychometrika. 1975. V. 40. P. 77–105.
42. Stroop G.R. Studies of interference of serial verbal reactions // Journal of Experimental Psychology. 1935. V. 18. P. 643–662.
43. Usher M., McClelland J.L. The time course of perceptual choice: the leaky, competing accumulator model // Psychological Review. 2001. V. 108. №3. P. 550–592.
44. Usher M., Zakay D. A neural network model for attribute-based decision processes // Cognitive Science. 1993. V. 17. P. 349–396.
45. Van Zandt T., Maldonado-Molina M. A mechanism for two-choice discrimination: time dependent response reversals in recognition memory // Fechner Day’2000: Proceedings of the 10th Annual Meeting of the International Society for Psychophysics (ISP) / Ed. by C. Bonnet. Strasbourg: France, 2000. P. 109–114.
46. Vickers D. Confidence and response time in three-category judgment // Fechner Day’2003: Proceedings of the 13th Annual Meeting of the International Society for Psychophysics (ISP) / Ed. by B. Berglund, E. Borg. Larnaka: Cyprus, 2003. P. 325–331.
47. Vickers D., Lee M. Dynamic models of simple judgments: I. Properties of a self-regulating accumulator model // Nonlinear dynamics, psychology and life sciences. 1998. V. 2. P. 169–194.
48. Vickers D., Lee M. Dynamic models of simple judgments: II. Properties of a self-organizing PAGAN (Parallel, Adaptive, Generalized Accumulator Network). Model for Multi-Choice Tasks // Nonlinear Dynamics, Psychology, and Life Sciences. 2000. V. 4. № 1. P. 1–31.